एनएलपी - वर्ड लेवल एनालिसिस
इस अध्याय में, हम प्राकृतिक भाषा प्रसंस्करण में विश्व स्तर के विश्लेषण को समझेंगे।
नियमित अभिव्यक्ति
एक नियमित अभिव्यक्ति (आरई) पाठ खोज स्ट्रिंग को निर्दिष्ट करने के लिए एक भाषा है। आरई हमें एक पैटर्न में आयोजित विशेष सिंटैक्स का उपयोग करते हुए, तार के अन्य तारों या सेटों को मिलाने या खोजने में मदद करता है। समान तरीके से UNIX के साथ-साथ MS WORD में ग्रंथों को खोजने के लिए नियमित अभिव्यक्तियों का उपयोग किया जाता है। हमारे पास कई आरई सुविधाओं का उपयोग करके विभिन्न खोज इंजन हैं।
नियमित भाव के गुण
अनुवर्ती आरई के कुछ महत्वपूर्ण गुण हैं -
अमेरिकी गणितज्ञ स्टीफन कोल क्लेन ने नियमित अभिव्यक्ति भाषा को औपचारिक रूप दिया।
आरई एक विशेष भाषा में एक सूत्र है, जिसका उपयोग सरल वर्गों के तार, प्रतीकों के अनुक्रम को निर्दिष्ट करने के लिए किया जा सकता है। दूसरे शब्दों में, हम कह सकते हैं कि आरई स्ट्रिंग्स के एक सेट को चिह्नित करने के लिए एक बीजीय संकेतन है।
नियमित अभिव्यक्ति के लिए दो चीजों की आवश्यकता होती है, एक वह पैटर्न है जिसे हम खोजना चाहते हैं और दूसरा वह पाठ का एक कोष है जिसमें से हमें खोज करने की आवश्यकता है।
गणितीय रूप से, एक नियमित अभिव्यक्ति को निम्नानुसार परिभाषित किया जा सकता है -
ε एक नियमित अभिव्यक्ति है, जो इंगित करता है कि भाषा एक खाली स्ट्रिंग है।
φ एक नियमित अभिव्यक्ति है जो यह दर्शाता है कि यह एक खाली भाषा है।
अगर X तथा Y रेगुलर एक्सप्रेशन हैं, फिर
X, Y
X.Y(Concatenation of XY)
X+Y (Union of X and Y)
X*, Y* (Kleen Closure of X and Y)
नियमित अभिव्यक्ति भी हैं।
यदि कोई स्ट्रिंग उपरोक्त नियमों से प्राप्त की जाती है तो वह भी एक नियमित अभिव्यक्ति होगी।
रेगुलर एक्सप्रेशन के उदाहरण
निम्न तालिका नियमित अभिव्यक्तियों के कुछ उदाहरण दिखाती है -
| नियमित अभिव्यक्ति | नियमित सेट |
|---|---|
| (0 + 10 *) | {, 1, 10, 100, 1000, 10000,…} |
| (0 * 10 *) | {, 01, 10, 010, 0010,…} |
| (0 + ε) (1 + ε) | {,, 0, 1, 01} |
| (ए + बी) * | यह किसी भी लम्बाई के a और b के तारों का सेट होगा जिसमें null string भी शामिल है अर्थात {ε, a, b, aa, ab, bb, ba, aaa ……।}। |
| (ए + बी) * एबीबी | यह स्ट्रिंग एब के साथ ए और बी के अंत के तारों का सेट होगा ({एबीबी, एएबीबी, बब्ब, आआब, एबब, ………… ..} |
| (1 1)* | यह 1 की सम संख्या से मिलकर बना होगा जिसमें एक खाली स्ट्रिंग भी शामिल है ({11, 11, 1111, 111111, ………।}। |
| (आ) * (bb) * ख | यह बी के समान संख्याओं से युक्त तारों के समूह के रूप में सेट किया जाएगा, जिसके बाद b की संख्या {b, aab, aabbb, abbbbb, aaaab, aaabbb, …………… ..} होगी |
| (आ + आब + बा + बीबी) * | यह a और b की एक समान लंबाई होगी, जिसे null यानी {aa, ab, ba, bb, aaab, aaba, ……… सहित स्ट्रिंग्स आ, ab, ba और bb के किसी भी संयोजन को प्राप्त करके प्राप्त किया जा सकता है। ।} |
नियमित सेट और उनके गुण
इसे उस सेट के रूप में परिभाषित किया जा सकता है जो नियमित अभिव्यक्ति के मूल्य का प्रतिनिधित्व करता है और इसमें विशिष्ट गुण होते हैं।
नियमित सेट के गुण
यदि हम दो नियमित सेटों का मिलन करते हैं तो परिणामी सेट भी रेगुला होगा।
यदि हम दो नियमित सेटों का प्रतिच्छेदन करते हैं तो परिणामी सेट भी नियमित होगा।
यदि हम नियमित सेटों के पूरक करते हैं, तो परिणामी सेट भी नियमित होगा।
यदि हम दो नियमित सेटों का अंतर करते हैं, तो परिणामी सेट भी नियमित होगा।
यदि हम नियमित सेटों को उलटते हैं, तो परिणामी सेट भी नियमित होगा।
यदि हम नियमित सेटों को बंद कर देते हैं, तो परिणामी सेट भी नियमित होगा।
यदि हम दो नियमित सेटों का संयोजन करते हैं, तो परिणामी सेट भी नियमित होगा।
परिमित स्टेट ऑटोमेटा
शब्द ऑटोमेटा, जो ग्रीक शब्द "ατμα "α" से लिया गया है, जिसका अर्थ है "स्व-अभिनय", ऑटोमेटन का बहुवचन है जिसे एक अमूर्त स्व-चालित कंप्यूटिंग डिवाइस के रूप में परिभाषित किया जा सकता है जो स्वचालित रूप से संचालन के पूर्वनिर्धारित अनुक्रम का अनुसरण करता है।
एक ऑटोमेटन में राज्यों की एक सीमित संख्या होती है, जिसे Finite Automaton (FA) या Finite State automata (FSA) कहा जाता है।
गणितीय रूप से, एक ऑटोमेटन को 5-ट्यूपल (क्यू, δ, δ, q0, F) द्वारा दर्शाया जा सकता है, जहां -
Q राज्यों का एक समुच्चय है।
Symbols प्रतीकों का एक परिमित सेट है, जिसे ऑटोमेटन की वर्णमाला कहा जाता है।
function संक्रमण कार्य है
q0 वह प्रारंभिक अवस्था है जहां से किसी भी इनपुट को संसाधित किया जाता है (q0) Q)।
F अंतिम अवस्था / Q के राज्यों (F set Q) का एक समूह है।
परिमित ऑटोमेटा, नियमित व्याकरण और नियमित अभिव्यक्तियों के बीच संबंध
निम्नलिखित बिंदु हमें परिमित ऑटोमेटा, नियमित व्याकरण और नियमित अभिव्यक्ति के बीच के संबंध के बारे में एक स्पष्ट दृष्टिकोण देंगे -
जैसा कि हम जानते हैं कि परिमित राज्य ऑटोमेटा कम्प्यूटेशनल कार्य का सैद्धांतिक आधार है और नियमित अभिव्यक्ति उनका वर्णन करने का एक तरीका है।
हम कह सकते हैं कि किसी भी नियमित अभिव्यक्ति को एफएसए के रूप में लागू किया जा सकता है और किसी भी एफएसए को एक नियमित अभिव्यक्ति के साथ वर्णित किया जा सकता है।
दूसरी ओर, नियमित अभिव्यक्ति एक तरह की भाषा है जिसे नियमित भाषा कहा जाता है। इसलिए, हम कह सकते हैं कि एफएसए और नियमित अभिव्यक्ति दोनों की मदद से नियमित भाषा का वर्णन किया जा सकता है।
नियमित व्याकरण, एक औपचारिक व्याकरण जो सही-नियमित या बाएं-नियमित हो सकता है, नियमित भाषा की विशेषता का एक और तरीका है।
निम्नलिखित आरेख से पता चलता है कि परिमित ऑटोमेटा, नियमित अभिव्यक्ति और नियमित व्याकरण नियमित भाषाओं के वर्णन के समान तरीके हैं।
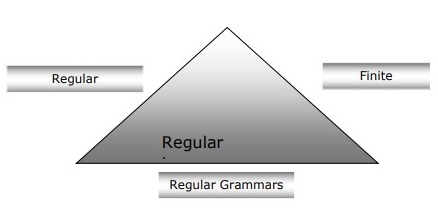
परिमित राज्य स्वचालन के प्रकार (FSA)
परिमित राज्य स्वचालन दो प्रकार का होता है। आइए हम देखें कि प्रकार क्या हैं।
नियतात्मक परिमित स्वचालन (DFA)
इसे परिमित स्वचालन के प्रकार के रूप में परिभाषित किया जा सकता है, जिसमें प्रत्येक इनपुट प्रतीक के लिए हम यह निर्धारित कर सकते हैं कि मशीन किस दिशा में जाएगी। इसमें राज्यों की सीमित संख्या है, इसीलिए मशीन को नियतात्मक परिमित ऑटोमेटन (DFA) कहा जाता है।
गणितीय रूप से, एक डीएफए को 5-ट्यूपल (क्यू, D, δ, q0, F) द्वारा दर्शाया जा सकता है, जहां -
Q राज्यों का एक समुच्चय है।
Symbols प्रतीकों का एक परिमित सेट है, जिसे ऑटोमेटन की वर्णमाला कहा जाता है।
Σ संक्रमण फ़ंक्शन है जहां δ: Q ×। → Q।
q0 वह प्रारंभिक अवस्था है जहां से किसी भी इनपुट को संसाधित किया जाता है (q0) Q)।
F अंतिम अवस्था / Q के राज्यों (F set Q) का एक समूह है।
जबकि ग्राफिक रूप से, एक डीएफए का चित्रण आरेखों द्वारा किया जा सकता है, जिसे राज्य चित्र कहा जाता है -
राज्यों द्वारा प्रतिनिधित्व किया जाता है vertices।
संक्रमण लेबल द्वारा दिखाए जाते हैं arcs।
प्रारंभिक अवस्था का प्रतिनिधित्व एक द्वारा किया जाता है empty incoming arc।
अंतिम स्थिति का प्रतिनिधित्व करता है double circle।
DFA का उदाहरण
मान लीजिए कि एक DFA हो
क्यू = {ए, बी, सी},
, = {0, 1},
q 0 = {a},
F = {c},
संक्रमण समारोह function तालिका में निम्नानुसार दिखाया गया है -
| वर्तमान स्थिति | इनपुट के लिए अगला राज्य 0 | इनपुट के लिए अगला राज्य 1 |
|---|---|---|
| ए | ए | ख |
| ख | ख | ए |
| सी | सी | सी |
इस डीएफए का चित्रमय प्रतिनिधित्व इस प्रकार होगा -

गैर-नियतात्मक परिमित स्वचालन (NDFA)
इसे परिमित स्वचालन के प्रकार के रूप में परिभाषित किया जा सकता है जहां हर इनपुट प्रतीक के लिए हम यह निर्धारित नहीं कर सकते हैं कि मशीन किस दिशा में जाएगी अर्थात मशीन राज्यों के किसी भी संयोजन में जा सकती है। इसमें राज्यों की एक सीमित संख्या है, यही वजह है कि मशीन को गैर-नियतात्मक परिमित स्वचालन (NDFA) कहा जाता है।
गणितीय रूप से, एनडीएफए का प्रतिनिधित्व 5-ट्यूपल (क्यू, δ, FA, q0, F) द्वारा किया जा सकता है, जहां -
Q राज्यों का एक समुच्चय है।
Symbols प्रतीकों का एक परिमित सेट है, जिसे ऑटोमेटन की वर्णमाला कहा जाता है।
δ: -इस संक्रमण समारोह जहां δ: Q × Q → 2 क्यू ।
q0: -प्रारंभिक स्थिति जहाँ से किसी भी इनपुट को संसाधित किया जाता है (q0) Q)।
एफ: -एस (एफ। क्यू) के अंतिम राज्य / राज्यों का एक सेट।
जबकि रेखांकन (डीएफए के समान), एक एनडीएफए को राज्य के आरेखों के आरेखों द्वारा दर्शाया जा सकता है जहां -
राज्यों द्वारा प्रतिनिधित्व किया जाता है vertices।
संक्रमण लेबल द्वारा दिखाए जाते हैं arcs।
प्रारंभिक अवस्था का प्रतिनिधित्व एक द्वारा किया जाता है empty incoming arc।
अंतिम स्थिति को दोहरे द्वारा दर्शाया गया है circle।
NDFA का उदाहरण
मान लीजिए कि एक NDFA हो
क्यू = {ए, बी, सी},
, = {0, 1},
q 0 = {a},
F = {c},
संक्रमण समारोह function तालिका में निम्नानुसार दिखाया गया है -
| वर्तमान स्थिति | इनपुट के लिए अगला राज्य 0 | इनपुट के लिए अगला राज्य 1 |
|---|---|---|
| ए | ए, बी | ख |
| ख | सी | एसी |
| सी | बी, सी | सी |
इस NDFA का चित्रमय प्रतिनिधित्व इस प्रकार होगा -

मॉर्फोलॉजिकल पार्सिंग
मॉर्फोलॉजिकल पार्सिंग शब्द मॉर्फेम के पार्सिंग से संबंधित है। हम रूपात्मक पार्सिंग को यह पहचानने की समस्या के रूप में परिभाषित कर सकते हैं कि एक शब्द छोटे सार्थक इकाइयों में टूट जाता है जिसे मोर्फेम कहा जाता है जो इसके लिए किसी प्रकार की भाषाई संरचना का निर्माण करता है। उदाहरण के लिए, हम शब्द तोड़ सकते हैं लोमड़ियों दो, में लोमड़ी और -es । हम देख सकते हैं कि शब्द लोमड़ी , दो मोर्फेम से बना है, एक लोमड़ी है और अन्य -स है ।
दूसरे अर्थ में, हम कह सकते हैं कि आकृति विज्ञान का अध्ययन है -
शब्दों का निर्माण।
शब्दों की उत्पत्ति।
शब्दों के व्याकरणिक रूप।
शब्दों के निर्माण में उपसर्गों और प्रत्ययों का प्रयोग।
किसी भाषा के भाग (भाषण) कैसे बनते हैं।
Morphemes के प्रकार
Morphemes, सबसे छोटी अर्थ-असर इकाइयाँ, को दो प्रकारों में विभाजित किया जा सकता है -
Stems
शब्द क्रम
उपजी
यह किसी शब्द की मूल सार्थक इकाई है। हम यह भी कह सकते हैं कि यह शब्द की जड़ है। उदाहरण के लिए, लोमड़ी शब्द में, तना लोमड़ी है।
Affixes- जैसा कि नाम से पता चलता है, वे शब्दों में कुछ अतिरिक्त अर्थ और व्याकरणिक कार्य जोड़ते हैं। उदाहरण के लिए, लोमड़ी शब्द में, एफिक्स है - तों।
इसके अलावा, प्रत्ययों को भी चार प्रकारों में विभाजित किया जा सकता है -
Prefixes- जैसा कि नाम से पता चलता है, उपसर्ग स्टेम से पहले है। उदाहरण के लिए, शब्द unbuckle में, un उपसर्ग है।
Suffixes- जैसा कि नाम से पता चलता है, प्रत्यय स्टेम का अनुसरण करते हैं। उदाहरण के लिए, शब्द में बिल्लियों, -s प्रत्यय है।
Infixes- जैसा कि नाम से पता चलता है, इन्फिक्स को स्टेम के अंदर डाला जाता है। उदाहरण के लिए, cupful शब्द, infix के रूप में -s का उपयोग करके cupful के रूप में बहुवचन हो सकता है।
Circumfixes- वे पूर्ववर्ती और स्टेम का पालन करते हैं। अंग्रेजी भाषा में परिधि के बहुत कम उदाहरण हैं। एक बहुत ही सामान्य उदाहरण 'ए-आईएनजी' है जहां हम उपयोग कर सकते हैं-पूर्ववर्ती और -इंग स्टेम का अनुसरण करता है।
शब्द क्रम
शब्दों का क्रम रूपात्मक पार्सिंग द्वारा तय किया जाएगा। आइए अब हम एक रूपात्मक पार्सर के निर्माण की आवश्यकताओं को देखें -
शब्दकोश
एक रूपात्मक पार्सर के निर्माण के लिए पहली आवश्यकता लेक्सिकॉन है, जिसमें उनके बारे में बुनियादी जानकारी के साथ-साथ उपजी और प्रत्ययों की सूची शामिल है। उदाहरण के लिए, जानकारी जैसे कि स्टेम नाउन स्टेम है या वर्ब स्टेम, आदि।
Morphotactics
यह मूल रूप से मॉर्फेम ऑर्डरिंग का मॉडल है। दूसरे अर्थ में, मॉडल यह समझाता है कि कौन से वर्ग के लोग किसी शब्द के अंदर अन्य वर्ग के महापुरुषों का अनुसरण कर सकते हैं। उदाहरण के लिए, मॉर्फोटैक्टिक तथ्य यह है कि अंग्रेजी बहुवचन morpheme हमेशा पूर्ववर्ती संज्ञा के बजाय संज्ञा का पालन करता है।
ऑर्थोग्राफिक नियम
ये वर्तनी नियम एक शब्द में होने वाले परिवर्तनों को मॉडल करने के लिए उपयोग किए जाते हैं। उदाहरण के लिए, y को शहर + जैसे शब्दों में परिवर्तित करने का नियम + शहर नहीं शहर।