गोलाकार दर्पणों द्वारा निर्मित चित्र

परिचय

किरण आरेखों को चित्रित करना एक आदर्श तरीका है जो गोलाकार दर्पणों द्वारा छवियों के निर्माण को चित्रित करता है।
कम से कम दो परावर्तित किरणों के प्रतिच्छेदन बिंदु वस्तु की छवि की सही स्थिति देते हैं।
निम्न तालिका एक द्वारा बनाई गई छवि को दर्शाती है concave mirror दिए गए ऑब्जेक्ट के विभिन्न पदों के लिए -

वस्तु की स्थिति	छवि की स्थिति	छवि का आकार	छवि की प्रकृति
अनंत पर	फोकस में एफ	अत्यधिक कम, इंगित किया गया	असली और उलटा
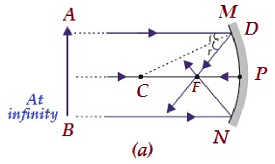
C के परे	बी / डब्ल्यू एफ और सी	कम	असली और उलटा
C पर	C पर	एक माप	असली और उलटा
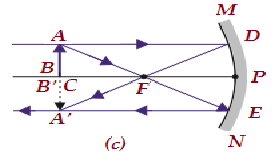
बी / डब्ल्यू सी और एफ	C के परे	बढ़ा हुआ	असली और उलटा
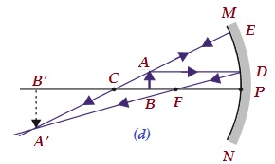
एफ पर	अनंत पर	अत्यधिक विस्तार	असली और उलटा
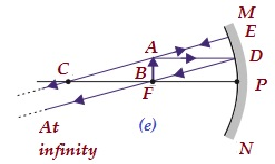
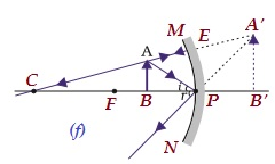
बी / डब्ल्यू पी और एफ	दर्पण के पीछे	बढ़ा हुआ	आभासी और सीधा

प्रकाश के शक्तिशाली समानांतर बीम प्राप्त करने के लिए, अवतल दर्पण सार्वभौमिक रूप से मशालों, खोज-रोशनी और वाहनों के हेडलाइट्स में उपयोग किए जाते हैं।
अवतल दर्पण का उपयोग नाई के सैलून में भी किया जाता है, क्योंकि यह बड़ा दृश्य देता है।
अवतल दर्पण का उपयोग दंत चिकित्सकों द्वारा भी किया जाता है, ताकि रोगियों के दांतों की बड़ी छवियों को देखा जा सके।
बड़े अवतल दर्पणों का उपयोग सूर्य की रोशनी को सौर भट्टियों में अधिकतम गर्मी उत्पन्न करने के लिए केंद्रित करने के लिए किया जाता है।

निम्न तालिका एक द्वारा बनाई गई छवि को दर्शाती है concave mirror दिए गए ऑब्जेक्ट के विभिन्न पदों के लिए -

वस्तु की स्थिति	छवि की स्थिति	छवि का आकार	छवि की प्रकृति	छवि
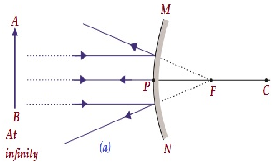
अनंत पर	दर्पण के पीछे फोकस एफ पर	अत्यधिक मंदता d, बिंदु आकार	आभासी और सीधा
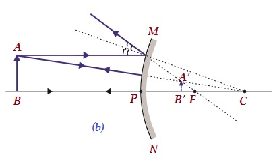
दर्पण के बी / डब्ल्यू अनंत और ध्रुव	दर्पण के पीछे बी / डब्ल्यू पी और एफ	Diminishe d	आभासी और सीधा

सभी वाहनों में, उत्तल दर्पणों को सार्वभौमिक रूप से रियर-व्यू (विंग) दर्पणों के रूप में उपयोग किया जाता है।
वाहनों में, उत्तल दर्पणों को प्राथमिकता दी जाती है, क्योंकि वे कम हो जाते हैं, लेकिन एक स्तंभित छवि।

$ $ \ frac {1} {v} + \ frac {1} {u} = \ frac {1} {}}}

दर्पण सूत्र वस्तु-दूरी (यानी) के बीच संबंधों को व्यक्त करता है u), छवि-दूरी (यानी v), और एक गोलाकार दर्पण की फोकल लंबाई (यानी एफ)।