पावर इलेक्ट्रॉनिक्स - हेलिकॉप्टर
एक हेलिकॉप्टर स्रोत लोड से कनेक्ट करने और डिस्कनेक्ट करने के लिए उच्च गति का उपयोग करता है। पावर स्विच ON / OFF को लगातार ट्रिगर करके एक निश्चित DC वोल्टेज को स्रोत लोड पर रुक-रुक कर लागू किया जाता है। उस समय की अवधि, जिसके लिए पावर स्विच ऑन या ऑफ रहता है, क्रमशः हेलिकॉप्टर के ऑन एंड ऑफ स्टेट समय के रूप में जाना जाता है।
हेलिकॉप्टर ज्यादातर इलेक्ट्रिक कारों, पवन और सौर ऊर्जा के रूपांतरण और डीसी मोटर नियामकों में लागू होते हैं।
एक चॉपर का प्रतीक
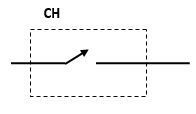
चॉपर्स का वर्गीकरण
वोल्टेज आउटपुट के आधार पर, हेलिकॉप्टरों को वर्गीकृत किया जाता है -
- स्टेप अप हेलिकॉप्टर (बूस्ट कन्वर्टर)
- स्टेप डाउन चॉपर (बक कन्वर्टर)
- स्टेप अप / डाउन चॉपर (बक-बूस्ट कन्वर्टर)
स्टेप अप चॉपर
स्टेप अप चॉपर में औसत वोल्टेज आउटपुट (V o ) वोल्टेज इनपुट (V s ) से अधिक होता है । नीचे दिया गया आंकड़ा स्टेप अप हेलिकॉप्टर के विन्यास को दर्शाता है।
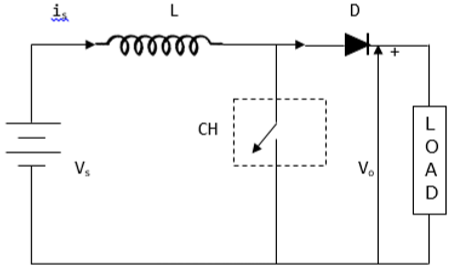
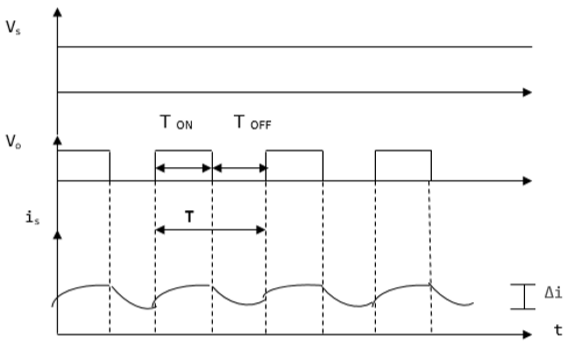
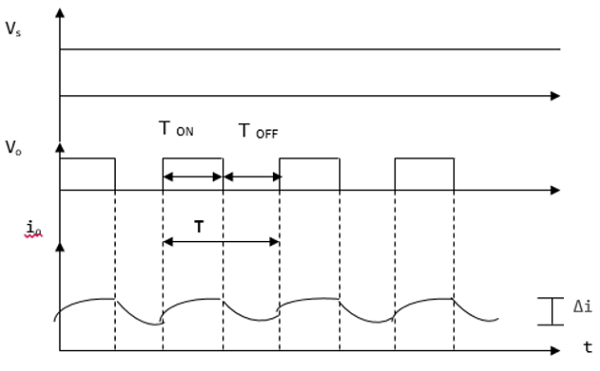
करंट और वोल्टेज वेवफॉर्म
वी 0 (औसत वोल्टेज आउटपुट) पॉजिटिव है जब हेलिकॉप्टर को चालू किया जाता है और नकारात्मक तब होता है जब हेलिकॉप्टर को नीचे की लहर में दिखाया जाता है।
कहाँ पे
टी पर समय अंतराल जब हेलिकॉप्टर चालू है
टी ऑफ - समय अंतराल जब हेलिकॉप्टर बंद है
वी एल - लोड वोल्टेज
वी एस - स्रोत वोल्टेज
T - समय अवधि काटना = T ON + T OFF
V o द्वारा दिया गया है -
$$ V_ {0} = \ frac {1} {टी} \ int_ {0} ^ {T_ {}} पर V_ {S} डीटी $$जब हेलिकॉप्टर (सीएच) को चालू किया जाता है, तो लोड कम परिचालित होता है और इसलिए, अवधि के लिए वोल्टेज आउटपुट TONशून्य है। इसके अलावा, प्रारंभ करनेवाला इस समय के दौरान चार्ज किया जाता है। इससे V S = V L मिलता है
$ L \ frac {di} {dt} = V_ {S}, $ $ \ frac {\ Delta i} {T_ {ON}} = \ frac {V_ {S}} {L} $
इसलिए, $ \ Delta i = \ frac {V_ {S}} {L} T_ {ON} $
Δi = एक प्रारंभ करनेवाला शिखर है जो वर्तमान में चोटी करता है। जब हेलिकॉप्टर (सीएच) बंद होता है, तो प्रारंभ करनेवाला एल के माध्यम से निर्वहन होता है। इसलिए, वी एस और वी एल का योग निम्नानुसार दिया गया है -
$ V_ {0} = V_ {S} + V_ {L}, \ Quad V_ {L} = V_ {0} -V_ {S} $
लेकिन $ L \ frac {di} {dt} = V_ {0} -V_ {S} $
इस प्रकार, $ L \ frac {\ Delta i} {T_ {OFF}} = V_ {0} -V_ {S} $
यह देता है, $ \ Delta i = \ frac {V_ {0} -V_ {S}} {L} T_ \ _ $
ऑफ स्टेट से toi को ON स्टेट से समीकरण देना -
$ \ frac {V_ {S}} {L} T_ {ON} = \ frac {V_ {0} -V_ {S}} {L} T_ {OFF} $, $ V_ {S} \ left (T {{ON) } + T_ {OFF} \ right) = V_ {0} T_ {OFF} $
$ V_ {0} = \ frac {TV_ {S}} {T_ {OFF}} = \ frac {V_ {S}} {\ frac {\ _ left (T + T_ {ON} \ right)} {T}} $
यह औसत वोल्टेज आउटपुट देता है,
$$ V_ {0} = \ frac {V_ {S}} {1-डी} $$उपरोक्त समीकरण से पता चलता है कि V o V S से अनंत तक भिन्न हो सकता है । यह साबित करता है कि आउटपुट वोल्टेज हमेशा वोल्टेज इनपुट से अधिक होगा और इसलिए, यह वोल्टेज स्तर को बढ़ाता है या बढ़ाता है।
स्टेप डाउन चॉपर
इसे हिरन कन्वर्टर के रूप में भी जाना जाता है। इस हेलिकॉप्टर में, औसत वोल्टेज आउटपुट V O इनपुट वोल्टेज V S से कम है । जब हेलिकॉप्टर चालू होता है, तो V O = V S और जब हेलिकॉप्टर बंद होता है, तो V O = 0
जब हेलिकॉप्टर चालू है -
$ V_ {S} = \ left (V_ {L} + V_ {0} \ right), \ quad V_ {L} = V_ {S} -V_ {0}, \ quad L \ frac {di} {d}} = V_ {S} -V_ {0}, \ quad L \ frac {\ Delta i} {T_ {ON}} = V_ {s} + V_ {0} $
इस प्रकार, पीक-टू-पीक वर्तमान लोड द्वारा दिया जाता है,
$ \ Delta i = \ frac {V_ {s} -V_ {0}} {L} T_ {ON}
सर्किट आरेख
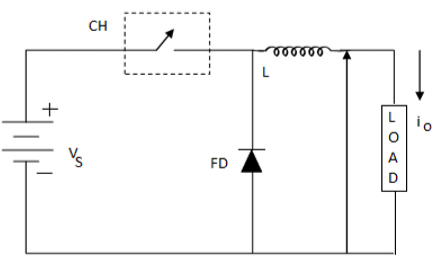
कहाँ पे FD फ्री-व्हील डायोड है।
जब हेलिकॉप्टर बंद हो जाता है, तो ध्रुवीय उलट होता है और प्रारंभ करनेवाला में निर्वहन होता है। वर्तमान फ्री-व्हील डायोड और प्रारंभ करनेवाला से लोड तक गुजरता है। यह देता है,
$$ एल \ frac {di} {डीटी} = V_ {0} .................................. ...... \ बाएँ (i \ दाएँ) $ $के रूप में फिर से लिखा - $ \ quad L \ frac {\ Delta i} {T_ {OFF}} = V_ {0} $
$$ \ Delta i = V_ {0} \ frac {T_ {OFF}} {L} ………………………। ...... \ बाएँ (ii \ दाएँ) $ $समीकरण समीकरण (i) और (ii) देता है;
$ \ Frac {V_ {S} -V_ {0}} {एल} T_ {} पर = \ frac {V_ {0}} {एल} T_ {} $ रवाना
$ \ Frac {V_ {S} -V_ {0}} {V_ {0}} = \ frac {T_ {बंद}} {T_ {}} पर $
$ \ Frac {V_ {S}} {V_ {0}} = \ frac {T_ {} पर -T_ {बंद}} {T_ {}} पर $
उपरोक्त समीकरण देता है;
$$ V_ {0} = \ frac {T_ {पर}} {टी} V_ {S} = DV_ {S} $$समीकरण (i) देता है -
$ \ Delta i = \ frac {V_ {S} -DV_ {S}} {L} DT $, $ D = \ frac {T_ {ON}} {T} $ से
$ = \ frac {V_ {S} - \ बाएँ (1-D \ दाएँ) D} {Lf} $
$ f = \ frac {1} {T} = $ चॉपिंग फ्रीक्वेंसी
करंट और वोल्टेज वेवफॉर्म
वर्तमान और वोल्टेज तरंग नीचे दिए गए हैं -
एक कदम नीचे हेलिकॉप्टर के लिए वोल्टेज आउटपुट हमेशा वोल्टेज इनपुट से कम होता है। यह नीचे तरंग द्वारा दिखाया गया है।
स्टेप अप / स्टेप डाउन चॉपर
इसे हिरन-बूस्टर कनवर्टर के रूप में भी जाना जाता है। यह वोल्टेज इनपुट स्तर को बढ़ाने या कम करने के लिए संभव बनाता है। नीचे दिए गए आरेख में एक हिरन को बढ़ावा देने वाला हेलिकॉप्टर दिखाया गया है।
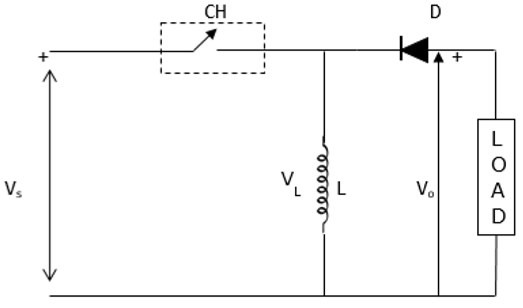
जब हेलिकॉप्टर को स्विच ऑन करने, प्रारंभ करनेवाला एल स्रोत वोल्टेज V द्वारा चार्ज हो जाता है रों । इसलिए, वी एस = वी एल ।
$ $ L \ frac {di} {dt} = V_ {S} $$ $$ \ Delta i = \ frac {V_ {S}} {L} T_ {ON} = \ frac {V_ {S}} / L } टी \ frac {T_ {पर}} {टी} = \ frac {DV_ {S}} {} वाम मोर्चे के $$क्योंकि -
$ D = \ frac {T_ {ON}} {T} $ और $ f = \ frac {1} {T} …………………। ....................... \ बाएँ (iii \ right) $
जब हेलिकॉप्टर को स्विच ऑफ किया जाता है, तो प्रारंभ करनेवाला की ध्रुवीयता उलट जाती है और इसके कारण यह डायोड और लोड के माध्यम से डिस्चार्ज हो जाता है।
इसलिये,
$ $ V_ {0} = - V_ {L} $ $ $ $ L \ frac {di} {dt} = - V_ {0} $ $$ L \ frac {\ Delta i} {T_ {OFF}} = - V_ {0} $, इस प्रकार $ \ Delta i = - \ frac {V_ {0}} {L} T_ {OFF} ..... ........................... \ left (iv \ right) $
मूल्यांकन समीकरण (iii) और (iv) देता है -
$ \ frac {DV_ {S}} {Lf} = - \ frac {V_ {0}} {L} T_ {OFF} $, $ DV_ {S} = - DV_ {S} = - V_ {0}: T_ { बंद} च $
US , $ V_ {0} = - \ frac {DV_ {S}} {1-D} $
क्योंकि $ D = \ frac {T_ {ON}} {T} = \ frac {T-T_ {OFF}} {1-D} $
यह देता है,
$ V_ {0} = \ frac {DV_ {S}} {1-डी} $
डी 0 से 1 तक भिन्न हो सकते हैं। जब, डी = 0; वी ओ = ०
जब डी = 0.5, वी ओ = वी एस
जब, डी = 1, वी ओ =,।
इसलिए, अंतराल 0 ≤ D output 0.5 में, आउटपुट वोल्टेज 0 O V O <V S रेंज में भिन्न होता है और हमें स्टेप डाउन या बक ऑपरेशन मिलता है। जबकि, अंतराल 0.5 ≤ डी ≤ 1 में, आउटपुट वोल्टेज रेंज वी में बदलता एस ≤ वी ओ ≤ ∞ और हम कदम उठना या बूस्ट आपरेशन।