आयाम अधिमिश्रण

मॉड्यूलेशन तकनीकों के प्रकारों में, मुख्य वर्गीकरण कंटीन्यूअस-वेव मॉड्यूलेशन और पल्स मॉड्यूलेशन है। निरंतर तरंग मॉड्यूलेशन तकनीकों को आगे विभाजित किया गया हैAmplitude Modulation तथा Angle Modulation।

एक निरंतर-तरंग बिना किसी अंतराल के लगातार चलती रहती है और यह बेसबैंड संदेश संकेत है, जिसमें सूचना होती है। इस लहर को संशोधित करना होगा।

मानक परिभाषा के अनुसार, "वाहक संकेत का आयाम modulating संकेत के तात्कालिक आयाम के अनुसार बदलता रहता है।" जिसका अर्थ है, वाहक संकेत का आयाम जिसमें कोई जानकारी नहीं है, संकेत के आयाम के अनुसार प्रत्येक पल में भिन्न होता है, जिसमें जानकारी होती है। यह निम्नलिखित आंकड़ों द्वारा अच्छी तरह से समझाया जा सकता है।

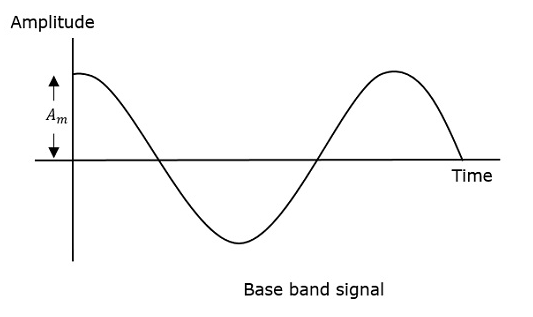
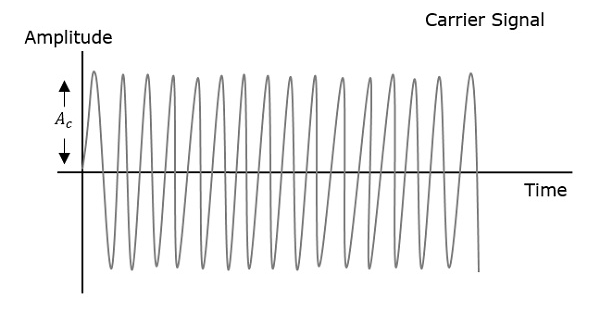
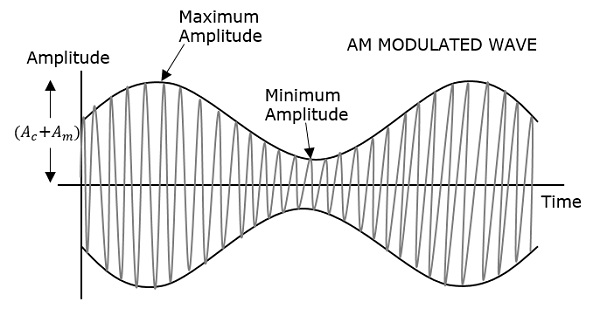
जो संदेश पहले दिखाया गया है वह मॉड्यूलेटिंग तरंग है। अगले एक वाहक लहर है, जो सिर्फ एक उच्च आवृत्ति संकेत है और इसमें कोई जानकारी नहीं है। जबकि अंतिम परिणामी संशोधित तरंग है।

यह देखा जा सकता है कि वाहक तरंग की सकारात्मक और नकारात्मक चोटियां, एक काल्पनिक रेखा के साथ परस्पर जुड़ी होती हैं। यह लाइन मॉड्यूलेटिंग सिग्नल के सटीक आकार को फिर से बनाने में मदद करती है। वाहक लहर पर इस काल्पनिक रेखा को कहा जाता हैEnvelope। यह संदेश संकेत के समान है।

गणितीय अभिव्यक्ति

इन तरंगों के लिए गणितीय अभिव्यक्ति निम्नलिखित हैं।

लहरों का समय-डोमेन प्रतिनिधित्व

सिग्नल को संशोधित करने दें -

$ $ m (t) = A_mcos (2 \ pi f_mt) $$

वाहक संकेत होने दें -

$ $ c (t) = A_ccos (2 \ pi f_ct) $$

कहाँ पे A_m = मॉड्यूलेटिंग सिग्नल का अधिकतम आयाम

A_c = वाहक संकेत का अधिकतम आयाम

एम्प्लिट्यूड मॉड्युलेटेड तरंग के मानक रूप को निम्नानुसार परिभाषित किया गया है -

$ $ S (t) = A_c [1 + K_am (t)] cos (2 \ pi f_ct) $$

$ $ S (t) = A_c [1+ \ mu cos (2 \ pi f_mt)] cos (2 \ pi f_ct) $$

$ $ कहां, \ mu = K_aA_m $$

मॉड्यूलेशन इंडेक्स

एक वाहक तरंग, संग्राहक होने के बाद, यदि संग्राहक स्तर की गणना की जाती है, तो इस तरह के प्रयास को कहा जाता है Modulation Index या Modulation Depth। यह मॉड्यूलेशन के स्तर को बताता है कि एक वाहक लहर गुजरती है।

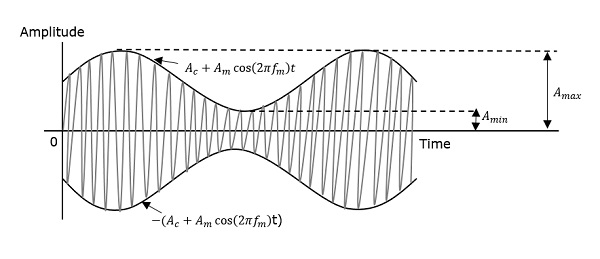
संग्राहक तरंग के लिफाफे के अधिकतम और न्यूनतम मूल्यों को क्रमशः ए _{अधिकतम} और ए _मिनट द्वारा दर्शाया जाता है।

आइए हम मॉड्यूलेशन इंडेक्स के लिए एक समीकरण विकसित करने का प्रयास करें।

$ $ A_ {अधिकतम} = A_c (1+ \ mu) $$

चूंकि, A _{अधिकतम} पर cos का मान 1 है

$$ A_ {min} = A_c (1- \ mu) $$

चूंकि, A _मिनट पर cos the का मान -1 है

$$ \ frac {A_ {अधिकतम}} {A_ {min}} = \ frac {1+ \ mu} {1- \ mu} $$

$ $ A_ {अधिकतम} - \ m A_ {अधिकतम} = A_ {min} + \ mu A_ {{}} $

$ $ - \ mu (A_ {अधिकतम} + A_ {min}) = A_ {min} -A_ {अधिकतम}% =

$$ \ mu = \ frac {A_ {max} -A_ {min}} {A_ {max} + A_ {min}} $$

इसलिए, मॉड्यूलेशन इंडेक्स के लिए समीकरण प्राप्त किया जाता है। µमॉड्यूलेशन इंडेक्स या मॉड्यूलेशन गहराई को दर्शाता है। इसे अक्सर प्रतिशत के रूप में चिह्नित किया जाता हैPercentage Modulation। यह प्रतिशत में निरूपित मॉड्यूलेशन की सीमा है, और इसके द्वारा निरूपित किया जाता हैm।

एक परिपूर्ण मॉड्यूलेशन के लिए, मॉड्यूलेशन इंडेक्स का मान 1 होना चाहिए, जिसका मतलब है कि मॉड्यूलेशन की गहराई 100% होनी चाहिए।

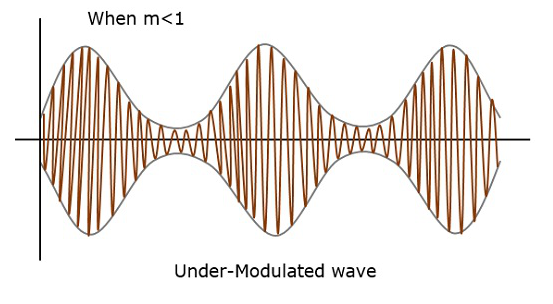
उदाहरण के लिए, यदि यह मान 1 से कम है, यानी, मॉड्यूलेशन इंडेक्स 0.5 है, तो मॉड्यूल्ड आउटपुट निम्न आंकड़े की तरह दिखेगा। इसे अंडर मॉड्यूलेशन कहा जाता है। इस तरह की एक लहर को एक कहा जाता हैunder-modulated wave।

यदि मॉड्यूलेशन इंडेक्स का मान 1, यानी 1.5 या उससे अधिक है, तो तरंग a होगी over-modulated wave। यह निम्न आकृति की तरह दिखेगा।

जैसे ही मॉड्यूलेशन इंडेक्स का मान बढ़ता है, वाहक 180 ° चरण उलट का अनुभव करता है, जो अतिरिक्त साइडबैंड का कारण बनता है और इसलिए, लहर विकृत हो जाती है। इस तरह की overmodulated लहर हस्तक्षेप का कारण बनती है, जिसे समाप्त नहीं किया जा सकता है।