अजगर - विभाजित और जीतना
विभाजित और जीत के दृष्टिकोण में, हाथ में समस्या, छोटी उप-समस्याओं में विभाजित होती है और फिर प्रत्येक समस्या को स्वतंत्र रूप से हल किया जाता है। जब हम उप-प्रकारों को छोटी-छोटी उप-समस्याओं में विभाजित करते रहते हैं, तो हम अंततः एक ऐसे चरण में पहुँच सकते हैं जहाँ कोई अधिक विभाजन संभव नहीं है। वे "परमाणु" सबसे छोटी संभव उप-समस्या (भिन्न) हल कर रहे हैं। सभी उप-समस्याओं का समाधान एक मूल समस्या का समाधान प्राप्त करने के लिए अंत में विलय कर दिया जाता है।
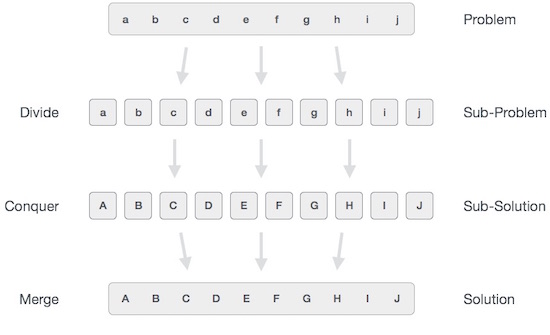
मोटे तौर पर, हम समझ सकते हैं divide-and-conquer तीन-चरणीय प्रक्रिया में दृष्टिकोण।
फूट डालो / तोड़
इस कदम में समस्या को छोटी उप-समस्याओं में तोड़ना शामिल है। उप-समस्याओं को मूल समस्या के एक हिस्से का प्रतिनिधित्व करना चाहिए। यह कदम आम तौर पर समस्या को विभाजित करने के लिए एक पुनरावर्ती दृष्टिकोण लेता है जब तक कि कोई उप-समस्या आगे विभाज्य न हो। इस स्तर पर, उप-समस्याएं प्रकृति में परमाणु बन जाती हैं लेकिन फिर भी वास्तविक समस्या के कुछ हिस्से का प्रतिनिधित्व करती हैं।
जीत / समाधान
इस चरण को हल करने के लिए बहुत छोटी उप-समस्याएं प्राप्त होती हैं। आमतौर पर, इस स्तर पर, समस्याओं को अपने आप में 'हल' माना जाता है।
मर्ज / कम्बाइन
जब छोटी उप-समस्याएं हल हो जाती हैं, तो यह चरण उन्हें पुन: संयोजित करता है जब तक कि वे मूल समस्या का समाधान तैयार नहीं करते। यह एल्गोरिथमिक दृष्टिकोण पुनरावर्ती रूप से काम करता है और जीतता है और मर्ज किए गए कदम इतने करीब आते हैं कि वे एक के रूप में दिखाई देते हैं।
उदाहरण
निम्नलिखित कार्यक्रम इसका एक उदाहरण है divide-and-conquer प्रोग्रामिंग दृष्टिकोण जहां बाइनरी खोज को अजगर का उपयोग करके कार्यान्वित किया जाता है।
बाइनरी खोज कार्यान्वयन
बाइनरी खोज में हम तत्वों की एक क्रमबद्ध सूची लेते हैं और सूची के मध्य में एक तत्व की तलाश शुरू करते हैं। यदि सूची में मध्य मान के साथ खोज मूल्य मेल खाता है तो हम खोज को पूरा करते हैं। अन्यथा हम खोजे गए आइटम के मूल्य के आधार पर सूची के दाएं या बाएं आधे हिस्से के साथ भविष्यवाणी करने के लिए चुनकर तत्वों की सूची का आधा हिस्सा निर्धारित करते हैं। यह संभव है क्योंकि सूची को क्रमबद्ध किया गया है और यह रैखिक खोज की तुलना में बहुत तेज है। यहां हम दी गई सूची को विभाजित करते हैं और सूची के उचित आधे को चुनकर जीतते हैं। हम इस दृष्टिकोण को तब तक दोहराते हैं जब तक हम तत्व को नहीं खोज लेते हैं या सूची में अनुपस्थिति के बारे में निष्कर्ष निकाल लेते हैं।
def bsearch(list, val):
list_size = len(list) - 1
idx0 = 0
idxn = list_size
# Find the middle most value
while idx0 <= idxn:
midval = (idx0 + idxn)// 2
if list[midval] == val:
return midval
# Compare the value the middle most value
if val > list[midval]:
idx0 = midval + 1
else:
idxn = midval - 1
if idx0 > idxn:
return None
# Initialize the sorted list
list = [2,7,19,34,53,72]
# Print the search result
print(bsearch(list,72))
print(bsearch(list,11))जब उपरोक्त कोड निष्पादित होता है, तो यह निम्नलिखित परिणाम उत्पन्न करता है:
5
None