कम्प्यूटेशनल रेखांकन
बैकप्रॉपैगमेंट को कम्प्यूटेशनल ग्राफ़ का उपयोग करके, गहन शिक्षण ढांचे जैसे कि टेंसोरफ़्लो, टॉर्च, थीनो आदि में लागू किया जाता है। अधिक महत्वपूर्ण रूप से, कम्प्यूटेशनल रेखांकन पर वापस प्रसार को समझना कई अलग-अलग एल्गोरिदम और इसके भिन्नरूपों को जोड़ता है जैसे कि समय के माध्यम से बैकप्रॉप और साझा भार के साथ बैकप्रॉप। एक बार जब सब कुछ एक कम्प्यूटेशनल ग्राफ में बदल जाता है, तो वे अभी भी एक ही एल्गोरिथ्म हैं - कम्प्यूटेशनल ग्राफ़ पर बस वापस प्रचार।
कम्प्यूटेशनल ग्राफ क्या है
एक कम्प्यूटेशनल ग्राफ को एक निर्देशित ग्राफ के रूप में परिभाषित किया जाता है जहां नोड्स गणितीय कार्यों के अनुरूप होते हैं। कम्प्यूटेशनल रेखांकन एक गणितीय अभिव्यक्ति को व्यक्त करने और मूल्यांकन करने का एक तरीका है।
उदाहरण के लिए, यहाँ एक सरल गणितीय समीकरण है -
$ $ p = x + y $$
हम उपरोक्त समीकरण के एक कम्प्यूटेशनल ग्राफ को निम्नानुसार आकर्षित कर सकते हैं।
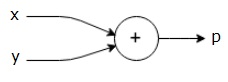
उपरोक्त कम्प्यूटेशनल ग्राफ में दो इनपुट चर x और y और एक आउटपुट q के साथ एक अतिरिक्त नोड ("+" चिह्न के साथ नोड) है।
हम एक और उदाहरण लेते हैं, थोड़ा और जटिल। हमारे पास निम्नलिखित समीकरण हैं।
$ $ g = \ left (x + y \ right) \ ast z $ $
उपरोक्त समीकरण को निम्नलिखित कम्प्यूटेशनल ग्राफ द्वारा दर्शाया गया है।
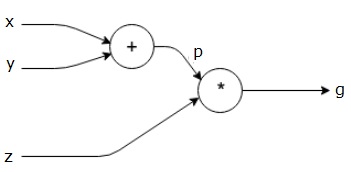
कम्प्यूटेशनल रेखांकन और Backpropagation
कम्प्यूटेशनल रेखांकन और बैकप्रोपैजेशन, दोनों तंत्रिका नेटवर्क के प्रशिक्षण के लिए गहन सीखने में महत्वपूर्ण मुख्य अवधारणाएं हैं।
अग्रवर्ती पारण
फॉरवर्ड पास कम्प्यूटेशनल रेखांकन द्वारा दर्शाए गए गणितीय अभिव्यक्ति के मूल्य का मूल्यांकन करने की प्रक्रिया है। फॉरवर्ड पास करने का मतलब है कि हम वेरिएबल्स से वैल्यू को लेफ्ट (इनपुट) से फॉरवर्ड दिशा में दाईं ओर पास कर रहे हैं जहां आउटपुट है।
आइए हम सभी इनपुट्स के लिए कुछ मूल्य देकर एक उदाहरण पर विचार करें। मान लीजिए, सभी इनपुट के लिए निम्न मान दिए गए हैं।
$ $ x = 1, y = 3, z = $3 $$
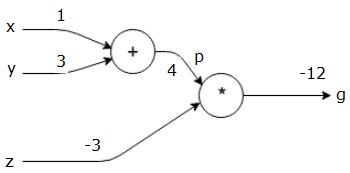
इनपुट्स को ये मान देकर, हम फॉरवर्ड पास का प्रदर्शन कर सकते हैं और प्रत्येक नोड पर आउटपुट के लिए निम्न मान प्राप्त कर सकते हैं।
सबसे पहले, हम p = 4 प्राप्त करने के लिए x = 1 और y = 3 के मान का उपयोग करते हैं।

फिर हम g = -12 प्राप्त करने के लिए p = 4 और z = -3 का उपयोग करते हैं। हम बाएं से दाएं, आगे की ओर जाते हैं।
बैकवर्ड पास के उद्देश्य
बैकवर्ड पास में, हमारा उद्देश्य अंतिम आउटपुट के संबंध में प्रत्येक इनपुट के लिए ग्रेडिएंट्स की गणना करना है। ये ग्रेडिएंट ग्रेडिएंट डिसेंट का उपयोग करके तंत्रिका नेटवर्क के प्रशिक्षण के लिए आवश्यक हैं।
उदाहरण के लिए, हम निम्नलिखित ढ़ाल की इच्छा रखते हैं।
वांछित ग्रेडिएंट्स
$$ \ frac {\ आंशिक x} {\ आंशिक f}, \ frac {\ आंशिक y} {\ आंशिक f}, \ frac {\ आंशिक z} {\ आंशिक f} $ $
बैकवर्ड पास (बैकप्रॉपैजेशन)
हम अंतिम आउटपुट के व्युत्पन्न को अंतिम आउटपुट (स्वयं!) के संबंध में खोजकर पिछड़ा पास शुरू करते हैं। इस प्रकार, यह पहचान व्युत्पत्ति में परिणाम देगा और मूल्य एक के बराबर है।
$ $ \ frac {\ आंशिक जी} {\ आंशिक जी} = 1 $ $
हमारा कम्प्यूटेशनल ग्राफ अब नीचे दिखाया गया है -
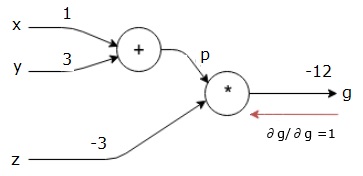
अगला, हम पिछड़े पास को "*" ऑपरेशन से करेंगे। हम p और z पर ग्रेडिएंट्स की गणना करेंगे। चूंकि g = p * z, हम जानते हैं कि -
$ $ \ frac {\ आंशिक जी} {\ आंशिक z} = पी $$
$ $ \ frac {\ आंशिक जी} {\ आंशिक पी} = जेड $ $
हम आगे पास से z और p के मूल्यों को पहले से ही जानते हैं। इसलिए, हम प्राप्त करते हैं -
$$ \ frac {\ आंशिक जी} {\ आंशिक z} = p = 4 $ $
तथा
$ $ \ frac {\ आंशिक जी} {\ आंशिक p} = z = -3 $ $
हम x और y पर ग्रेडिएंट की गणना करना चाहते हैं -
$$ \ frac {\ आंशिक जी} {\ आंशिक x}, \ frac {\ आंशिक जी} {{आंशिक y} $ $
हालाँकि, हम इसे कुशलतापूर्वक करना चाहते हैं (हालाँकि x और g इस ग्राफ में केवल दो हॉप्स हैं, कल्पना करें कि वे वास्तव में एक दूसरे से बहुत दूर हैं)। इन मूल्यों की कुशलता से गणना करने के लिए, हम भेदभाव के श्रृंखला नियम का उपयोग करेंगे। चेन शासन से, हमारे पास है -
$$ \ frac {\ आंशिक g} {\ आंशिक x} = \ frac {\ आंशिक g} {\ आंशिक p} \ ast \ frac {\ आंशिक p} {\ आंशिक x} $ $
$$ \ frac {\ आंशिक g} {\ आंशिक y} = \ frac {\ आंशिक g} {\ आंशिक p} \ ast \ frac {\ आंशिक p} {\ आंशिक y} $$
लेकिन हम पहले से ही जानते हैं कि dg / dp = -3, dp / dx और dp / dy आसान है क्योंकि p सीधे x और y पर निर्भर करता है। हमारे पास है -
$ $ p = x + y \ Rightarrow \ frac {\ आंशिक x} {\ आंशिक p} = 1, \ frac {\ आंशिक y} {\ आंशिक p} = 1 $ $
इसलिए, हम प्राप्त करते हैं -
$$ \ frac {\ आंशिक g} {\ आंशिक f} = \ frac {\ आंशिक g} {\ आंशिक p} \ ast \ frac {\ आंशिक p} {\ आंशिक x} = \ बाएँ (-3 \ दाएँ) .1 = -3 $ $
इसके अलावा, इनपुट y के लिए -
$$ \ frac {\ आंशिक g} {\ आंशिक y} = \ frac {\ आंशिक g} {\ आंशिक p} \ ast \ frac {\ आंशिक p} {\ आंशिक y} = \ बाएँ (-3 \ सही) .1 = -3 $ $
इसे पीछे करने का मुख्य कारण यह है कि जब हमें एक्स पर ग्रेडिएंट की गणना करनी थी, तो हमने केवल पहले से ही गणना किए गए मानों का उपयोग किया, और dq / dx (समान नोड के इनपुट के संबंध में नोड आउटपुट का व्युत्पन्न)। हमने वैश्विक मूल्य की गणना करने के लिए स्थानीय जानकारी का उपयोग किया।
एक तंत्रिका नेटवर्क के प्रशिक्षण के लिए कदम
तंत्रिका नेटवर्क को प्रशिक्षित करने के लिए इन चरणों का पालन करें -
डेटा पॉइंट x के लिए डेटासेट में, हम इनपुट के रूप में x के साथ फॉरवर्ड पास करते हैं, और आउटपुट के रूप में लागत c की गणना करते हैं।
हम सी पर शुरू होने वाले बैकवर्ड पास करते हैं, और ग्राफ में सभी नोड्स के लिए ग्रेडिएंट्स की गणना करते हैं। इसमें नोड्स शामिल हैं जो तंत्रिका नेटवर्क भार का प्रतिनिधित्व करते हैं।
हम फिर W = W - लर्निंग रेट * ग्रेडिएंट्स करके वेट अपडेट करते हैं।
हम इस प्रक्रिया को तब तक दोहराते हैं जब तक स्टॉप मापदंड पूरा नहीं हो जाता।