PyTorch - रैखिक प्रतिगमन
इस अध्याय में, हम TensorFlow का उपयोग करके रैखिक प्रतिगमन कार्यान्वयन के मूल उदाहरण पर ध्यान केंद्रित करेंगे। लॉजिस्टिक रिग्रेशन या लीनियर रिग्रेशन ऑर्डर डिसक्रीट श्रेणियों के वर्गीकरण के लिए एक पर्यवेक्षित मशीन लर्निंग अप्रोच है। इस अध्याय में हमारा लक्ष्य एक मॉडल का निर्माण करना है जिसके द्वारा एक उपयोगकर्ता भविष्यवक्ता चर और एक या अधिक स्वतंत्र चर के बीच संबंधों की भविष्यवाणी कर सकता है।
इन दो चर के बीच संबंध को रैखिक माना जाता है अर्थात, यदि y आश्रित चर है और x को स्वतंत्र चर माना जाता है, तो दो चर के रैखिक प्रतिगमन संबंध उस समीकरण की तरह दिखाई देंगे जिसका उल्लेख नीचे दिया गया है -
Y = Ax+bअगला, हम रैखिक प्रतिगमन के लिए एक एल्गोरिथ्म डिजाइन करेंगे जो हमें नीचे दिए गए दो महत्वपूर्ण अवधारणाओं को समझने की अनुमति देता है -
- लागत कार्य
- ग्रेडिएंट डिसेंट अल्गोरिथम
रैखिक प्रतिगमन का योजनाबद्ध प्रतिनिधित्व नीचे वर्णित है
परिणाम की व्याख्या करना
$$ वाई = ax + b $$
का मूल्य a ढलान है।
का मूल्य b है y − intercept।
r है correlation coefficient।
r2 है correlation coefficient।
रेखीय प्रतिगमन के समीकरण का ग्राफिकल दृश्य नीचे उल्लिखित है -

निम्नलिखित चरणों का उपयोग PyTorch का उपयोग करके रैखिक प्रतिगमन को लागू करने के लिए किया जाता है -
चरण 1
नीचे दिए गए कोड का उपयोग करके PyTorch में एक रेखीय प्रतिगमन बनाने के लिए आवश्यक संकुल आयात करें -
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
import seaborn as sns
import pandas as pd
%matplotlib inline
sns.set_style(style = 'whitegrid')
plt.rcParams["patch.force_edgecolor"] = Trueचरण 2
नीचे दिखाए गए अनुसार उपलब्ध डेटा सेट के साथ एकल प्रशिक्षण सेट बनाएं -
m = 2 # slope
c = 3 # interceptm = 2 # slope
c = 3 # intercept
x = np.random.rand(256)
noise = np.random.randn(256) / 4
y = x * m + c + noise
df = pd.DataFrame()
df['x'] = x
df['y'] = y
sns.lmplot(x ='x', y ='y', data = df)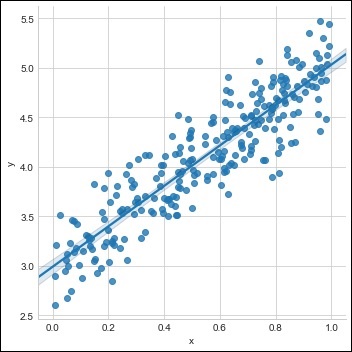
चरण 3
नीचे वर्णित के रूप में PyTorch पुस्तकालयों के साथ रैखिक प्रतिगमन को लागू करें -
import torch
import torch.nn as nn
from torch.autograd import Variable
x_train = x.reshape(-1, 1).astype('float32')
y_train = y.reshape(-1, 1).astype('float32')
class LinearRegressionModel(nn.Module):
def __init__(self, input_dim, output_dim):
super(LinearRegressionModel, self).__init__()
self.linear = nn.Linear(input_dim, output_dim)
def forward(self, x):
out = self.linear(x)
return out
input_dim = x_train.shape[1]
output_dim = y_train.shape[1]
input_dim, output_dim(1, 1)
model = LinearRegressionModel(input_dim, output_dim)
criterion = nn.MSELoss()
[w, b] = model.parameters()
def get_param_values():
return w.data[0][0], b.data[0]
def plot_current_fit(title = ""):
plt.figure(figsize = (12,4))
plt.title(title)
plt.scatter(x, y, s = 8)
w1 = w.data[0][0]
b1 = b.data[0]
x1 = np.array([0., 1.])
y1 = x1 * w1 + b1
plt.plot(x1, y1, 'r', label = 'Current Fit ({:.3f}, {:.3f})'.format(w1, b1))
plt.xlabel('x (input)')
plt.ylabel('y (target)')
plt.legend()
plt.show()
plot_current_fit('Before training')उत्पन्न की गई साजिश इस प्रकार है -
