आर - नॉनलाइनियर लेस्टर स्क्वायर
जब प्रतिगमन विश्लेषण के लिए वास्तविक विश्व डेटा मॉडलिंग करते हैं, तो हम मानते हैं कि यह शायद ही कभी ऐसा होता है कि मॉडल का समीकरण एक रेखीय समीकरण है जो एक रेखीय ग्राफ देता है। अधिकांश समय, वास्तविक विश्व डेटा के मॉडल के समीकरण में उच्च डिग्री के गणितीय कार्य शामिल होते हैं जैसे 3 या एक पाप फ़ंक्शन के घातांक। ऐसे में मॉडल का प्लॉट लाइन के बजाय कर्व देता है। रैखिक और गैर-रेखीय दोनों प्रतिगमन का लक्ष्य मॉडल के मापदंडों के मूल्यों को समायोजित करने के लिए है जो आपके डेटा के करीब आने वाली रेखा या वक्र को खोजने के लिए है। इन मूल्यों को खोजने पर हम अच्छी सटीकता के साथ प्रतिक्रिया चर का अनुमान लगाने में सक्षम होंगे।
कम से कम वर्ग स्क्वायर प्रतिगमन में, हम एक प्रतिगमन मॉडल स्थापित करते हैं जिसमें प्रतिगमन वक्र से विभिन्न बिंदुओं के ऊर्ध्वाधर दूरी के वर्गों का योग कम से कम किया जाता है। हम आम तौर पर एक परिभाषित मॉडल के साथ शुरू करते हैं और गुणांक के लिए कुछ मूल्यों को मानते हैं। हम फिर आवेदन करते हैंnls() विश्वास अंतराल के साथ अधिक सटीक मान प्राप्त करने के लिए R का कार्य।
वाक्य - विन्यास
R में एक नॉनलाइनियर कम से कम वर्ग परीक्षण बनाने का मूल सिंटैक्स है -
nls(formula, data, start)निम्नलिखित मापदंडों का वर्णन है -
formula एक गैर-मॉडल मॉडल है जिसमें चर और पैरामीटर शामिल हैं।
data सूत्र में चर का मूल्यांकन करने के लिए उपयोग किया जाने वाला डेटा फ़्रेम है।
start अनुमानित नामों की एक सूची या नामांकित वेक्टर वेक्टर है।
उदाहरण
हम अपने गुणांक के प्रारंभिक मूल्यों की धारणा के साथ एक nonlinear मॉडल पर विचार करेंगे। आगे हम देखेंगे कि इन ग्रहण किए गए मूल्यों का आत्मविश्वास अंतराल क्या है ताकि हम यह अनुमान लगा सकें कि ये मूल्य मॉडल में कितना अच्छा है।
तो आइए इस उद्देश्य के लिए नीचे दिए गए समीकरण पर विचार करें -
a = b1*x^2+b2आइए प्रारंभिक गुणांक को 1 और 3 मानें और इन मानों को nls () फ़ंक्शन में फिट करें।
xvalues <- c(1.6,2.1,2,2.23,3.71,3.25,3.4,3.86,1.19,2.21)
yvalues <- c(5.19,7.43,6.94,8.11,18.75,14.88,16.06,19.12,3.21,7.58)
# Give the chart file a name.
png(file = "nls.png")
# Plot these values.
plot(xvalues,yvalues)
# Take the assumed values and fit into the model.
model <- nls(yvalues ~ b1*xvalues^2+b2,start = list(b1 = 1,b2 = 3))
# Plot the chart with new data by fitting it to a prediction from 100 data points.
new.data <- data.frame(xvalues = seq(min(xvalues),max(xvalues),len = 100))
lines(new.data$xvalues,predict(model,newdata = new.data))
# Save the file.
dev.off()
# Get the sum of the squared residuals.
print(sum(resid(model)^2))
# Get the confidence intervals on the chosen values of the coefficients.
print(confint(model))जब हम उपरोक्त कोड निष्पादित करते हैं, तो यह निम्नलिखित परिणाम उत्पन्न करता है -
[1] 1.081935
Waiting for profiling to be done...
2.5% 97.5%
b1 1.137708 1.253135
b2 1.497364 2.496484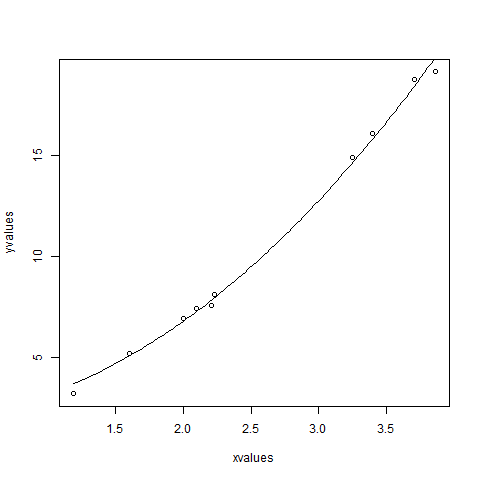
हम यह निष्कर्ष निकाल सकते हैं कि b1 का मान 1 के अधिक निकट है जबकि b2 का मान 2 के अधिक निकट है और 3 नहीं है।