उपग्रह संचार - कक्षीय यांत्रिकी
हम जानते हैं कि पृथ्वी के चारों ओर घूमने वाले उपग्रह का मार्ग किसके रूप में जाना जाता है orbit। इस पथ को गणितीय संकेतन के साथ दर्शाया जा सकता है। ऑर्बिटल मैकेनिक्स उन उपग्रहों की गति का अध्ययन है जो कक्षाओं में मौजूद हैं। इसलिए, हम कक्षीय गति के ज्ञान के साथ अंतरिक्ष संचालन को आसानी से समझ सकते हैं।
कक्षीय तत्व
कक्षीय तत्व पैरामीटर हैं, जो उपग्रहों की कक्षीय गति का वर्णन करने के लिए सहायक हैं। निम्नलिखित हैंorbital elements।
- सेमीमेजर एक्सिस
- Eccentricity
- मतलब विसंगति
- पेरिगी का तर्क
- Inclination
- आरोही नोड का दाहिना भाग
उपरोक्त छह कक्षीय तत्व पृथ्वी के उपग्रहों की कक्षा को परिभाषित करते हैं। इसलिए, कक्षीय तत्वों के मूल्यों के आधार पर अन्य उपग्रहों में से एक उपग्रह को भेदभाव करना आसान है।
सेमीमेजर एक्सिस
इसकी लंबाई Semi-major axis (a)उपग्रह की कक्षा के आकार को परिभाषित करता है। यह प्रमुख अक्ष का आधा है। यह केंद्र से फोकस के किनारे तक चलता है। तो, यह कक्षा के दो सबसे दूर बिंदुओं पर एक कक्षा की त्रिज्या है।
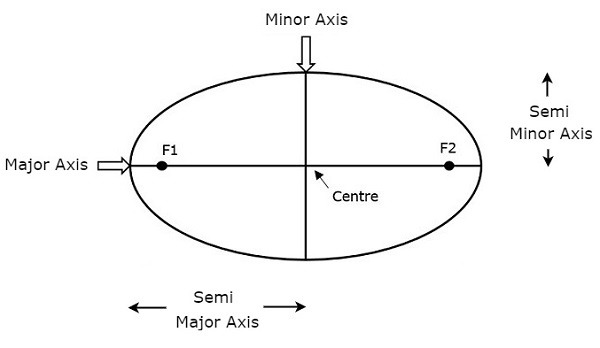
उपरी आकृति में अर्ध प्रमुख अक्ष और अर्ध लघु अक्ष दोनों का प्रतिनिधित्व किया जाता है। सेमी की लंबाईmajor axis (a) न केवल उपग्रह की कक्षा का आकार, बल्कि क्रांति की समय अवधि भी निर्धारित करता है।
यदि वृत्ताकार कक्षा को एक विशेष स्थिति के रूप में माना जाता है, तो अर्ध-प्रमुख अक्ष की लंबाई के बराबर होगी radius उस वृत्ताकार कक्षा की।
सनक
का मूल्य Eccentricity (e)उपग्रह की कक्षा के आकार को ठीक करता है। यह पैरामीटर एक सही सर्कल से कक्षा की आकृति के विचलन को इंगित करता है।
यदि अण्डाकार कक्षा के अर्ध प्रमुख अक्ष और अर्ध लघु अक्ष की लंबाई एक & b है, तो गणितीय अभिव्यक्ति के लिए eccentricity (e) होगा
$$ e = \ frac {\ sqrt {a 2 - b ^ 2}} {a} $ $
एक वृत्ताकार कक्षा की विलक्षणता का मूल्य है zero, चूँकि दोनों a & b बराबर हैं। जबकि, अण्डाकार कक्षा की विलक्षणता का मूल्य शून्य और एक के बीच है।
निम्नलिखित figure विभिन्न सनकी (ई) मूल्यों के लिए विभिन्न उपग्रह कक्षाओं को दर्शाता है
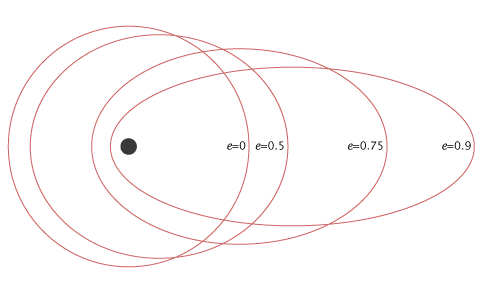
उपरोक्त आकृति में, शून्य की मानदण्ड (e) मूल्य के अनुरूप उपग्रह कक्षा एक गोलाकार कक्षा है। और, शेष तीन उपग्रह कक्षा विलक्षणता (ई) मान 0.5, 0.75 और 0.9 के अनुरूप अण्डाकार के हैं।
मतलब अनोमली
एक उपग्रह के लिए, वह बिंदु जो पृथ्वी से निकटतम है, पेरिगी के रूप में जाना जाता है। Mean anomaly (एम) पेरिगी के संदर्भ में उपग्रह की कोणीय स्थिति का औसत मूल्य देता है।
यदि कक्षा गोलाकार है, तो मीन विसंगति कक्षा में उपग्रह की कोणीय स्थिति देती है। लेकिन, यदि कक्षा अण्डाकार है, तो सटीक स्थिति की गणना बहुत मुश्किल है। उस समय, माध्य विसंगति का उपयोग एक मध्यवर्ती कदम के रूप में किया जाता है।
पेरीगी का तर्क
उपग्रह कक्षा दो स्थानों पर भूमध्यरेखा को काटता है। पहले बिंदु के रूप में कहा जाता हैdescending node, जहां उपग्रह उत्तरी गोलार्ध से दक्षिणी गोलार्ध तक जाता है। दूसरा बिंदु के रूप में कहा जाता हैascending node, जहां उपग्रह दक्षिणी गोलार्ध से उत्तरी गोलार्ध तक जाता है।
Argument of perigee (ω)आरोही नोड और पेरिगी के बीच का कोण है। यदि पेरिगी और आरोही नोड दोनों एक ही बिंदु पर मौजूद हैं, तो पेरिगी का तर्क शून्य डिग्री होगा
उपग्रह गति की दिशा में पृथ्वी के केंद्र में कक्षीय विमान से आघात की माप की जाती है।
झुकाव
कक्षीय समतल और पृथ्वी के भूमध्य रेखा के बीच के कोण को कहा जाता है inclination (i)। यह उत्तर से पूर्व की ओर होने के साथ आरोही नोड पर मापा जाता है। तो, झुकाव पृथ्वी के भूमध्य रेखा को संदर्भ के रूप में मानकर कक्षा के उन्मुखीकरण को परिभाषित करता है।

झुकाव के कोण के आधार पर चार प्रकार की कक्षाएँ हैं।
Equatorial orbit - झुकाव का कोण या तो शून्य डिग्री या 180 डिग्री है।
Polar orbit - झुकाव का कोण 90 डिग्री है।
Prograde orbit - झुकाव का कोण शून्य और 90 डिग्री के बीच होता है।
Retrograde orbit - झुकाव का कोण 90 और 180 डिग्री के बीच होता है।
आरोही नोड का सही उदगम
हम जानते हैं कि ascending node वह बिंदु है, जहां दक्षिणी गोलार्ध से उत्तरी गोलार्ध में जाने के दौरान उपग्रह भूमध्यरेखा को पार करता है।
आरोही नोड का सही उदगम (Ω)भूमध्य रेखा में पूर्व दिशा की ओर मेष और आरोही नोड की रेखा के बीच का कोण है। मेष राशि को वैवाहिक और विषुव भी कहा जाता है।
उपग्रह की ground trackपृथ्वी की सतह पर पथ है, जो अपनी कक्षा के बिल्कुल नीचे स्थित है। उपग्रह का ग्राउंड ट्रैक कक्षीय तत्वों के मूल्यों के आधार पर कई अलग-अलग रूप ले सकता है।
कक्षीय समीकरण
इस खंड में, हम उन समीकरणों के बारे में चर्चा करते हैं जो कक्षीय गति से संबंधित हैं।
उपग्रह पर अभिनय करने वाले बल
एक उपग्रह, जब यह पृथ्वी के चारों ओर घूमता है, तो यह पृथ्वी के गुरुत्वाकर्षण बल के कारण पृथ्वी से एक पुलिंग बल से गुजरता है। इस बल के रूप में जाना जाता हैCentripetal force(F 1 ) क्योंकि यह बल उपग्रह को अपनी ओर खींचता है।
गणितीय रूप से, द Centripetal force(एफ 1 ) पृथ्वी के कारण उपग्रह पर अभिनय के रूप में लिखा जा सकता है
$ $ F_ {1} = \ frac {GMm} {R ^ 2} $ $
कहाँ पे,
Gसार्वभौमिक गुरुत्वाकर्षण स्थिरांक है और यह 6.673 x 10 -11 N rav m 2 / kg 2 के बराबर है ।
Mपृथ्वी का द्रव्यमान है और यह 5.98 x 10 24 किलोग्राम के बराबर है ।
m उपग्रह का द्रव्यमान है।
R पृथ्वी के केंद्र से उपग्रह की दूरी है।
एक उपग्रह, जब यह पृथ्वी के चारों ओर घूमता है, तो यह अपने गुरुत्वाकर्षण बलों के कारण सूर्य और चंद्रमा से एक पुलिंग बल से गुजरता है। इस बल के रूप में जाना जाता हैCentrifugal force(F 2 ) क्योंकि यह बल उपग्रह को पृथ्वी से दूर ले जाता है।
गणितीय रूप से, द Centrifugal force(F 2 ) उपग्रह पर अभिनय के रूप में लिखा जा सकता है
$ $ F_ {2} = \ frac {mv ^ 2} {R} $ $
कहाँ पे, v उपग्रह का कक्षीय वेग है।
कक्षीय वेग
उपग्रह का कक्षीय वेग वह वेग है जिस पर उपग्रह पृथ्वी के चारों ओर घूमता है। उपग्रह अपनी कक्षा से विचलन नहीं करता है और उस कक्षा में कुछ वेग के साथ गति करता है, जब दोनों केंद्र और केन्द्रापसारक बल होते हैंbalance एक दूसरे।
इसलिए, equateCentripetal Force (F 1 ) और Centrifugal Force (F 2 )।
$$ \ frac {GMm} {R ^ 2} = \ frac {mv ^ 2} {R} $ $
$ $ => \ frac {GM} {R} = v ^ 2 $ $
$ $ => v = \ sqrt {\ frac {GM} {R}} $ $
इसलिए orbital velocity उपग्रह का है
$ $ v = \ sqrt {\ frac {GM} {R}} $ $
कहाँ पे,
Gगुरुत्वाकर्षण स्थिरांक है और यह 6.673 x 10 -11 N it m 2 / kg 2 के बराबर है ।
Mपृथ्वी का द्रव्यमान है और यह 5.98 x 10 24 किलोग्राम के बराबर है ।
R पृथ्वी के केंद्र से उपग्रह की दूरी है।
तो, मुख्य रूप से कक्षीय वेग depends पृथ्वी से उपग्रह के केंद्र (R) की दूरी पर, चूंकि G & M स्थिरांक हैं।