TensorFlow - गणितीय नींव
TensorFlow में मूल एप्लिकेशन बनाने से पहले TensorFlow के लिए आवश्यक गणितीय अवधारणाओं को समझना महत्वपूर्ण है। गणित को किसी भी मशीन लर्निंग एल्गोरिदम का दिल माना जाता है। यह गणित की मुख्य अवधारणाओं की मदद से है, विशिष्ट मशीन लर्निंग एल्गोरिदम के लिए एक समाधान परिभाषित किया गया है।
वेक्टर
संख्याओं की एक सरणी, जो या तो निरंतर या असतत होती है, को वेक्टर के रूप में परिभाषित किया जाता है। बेहतर लर्निंग आउटपुट के लिए मशीन लर्निंग एल्गोरिदम तय लंबाई वाले वैक्टर से निपटते हैं।
मशीन लर्निंग एल्गोरिदम बहुआयामी डेटा से निपटते हैं इसलिए वैक्टर एक महत्वपूर्ण भूमिका निभाते हैं।

वेक्टर मॉडल का सचित्र प्रतिनिधित्व नीचे दिखाया गया है -
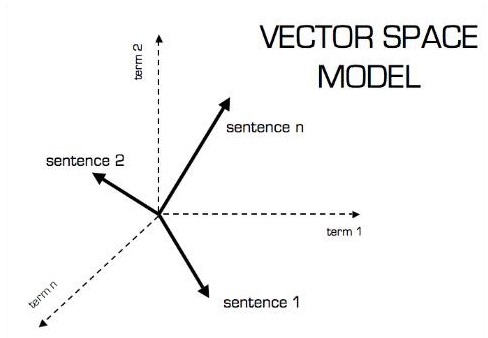
अदिश
स्केलर को एक आयामी वेक्टर के रूप में परिभाषित किया जा सकता है। स्केलर वे होते हैं, जिनमें केवल परिमाण और कोई दिशा नहीं होती है। स्केलर के साथ, हम केवल परिमाण के साथ चिंतित हैं।
स्केलर के उदाहरणों में बच्चों का वजन और ऊंचाई पैरामीटर शामिल हैं।
आव्यूह
मैट्रिक्स को बहुआयामी सरणियों के रूप में परिभाषित किया जा सकता है, जिन्हें पंक्तियों और स्तंभों के प्रारूप में व्यवस्थित किया जाता है। मैट्रिक्स का आकार पंक्ति की लंबाई और स्तंभ की लंबाई से परिभाषित होता है। निम्नलिखित आंकड़ा किसी भी निर्दिष्ट मैट्रिक्स का प्रतिनिधित्व दर्शाता है।
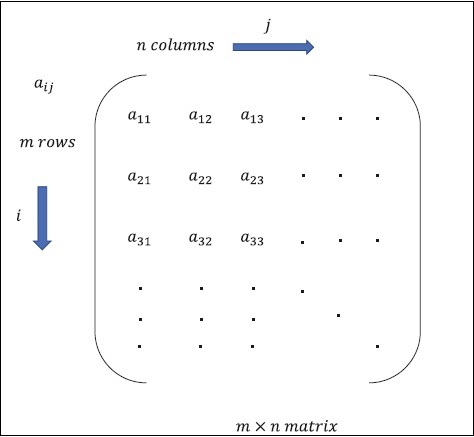
मैट्रिक्स का उल्लेख "m" पंक्तियों और "n" कॉलम के साथ करें जैसा कि ऊपर उल्लेख किया गया है, मैट्रिक्स प्रतिनिधित्व "m * n मैट्रिक्स" के रूप में निर्दिष्ट किया जाएगा जो मैट्रिक्स की लंबाई को भी परिभाषित करता है।
गणितीय संगणना
इस खंड में, हम TensorFlow में विभिन्न गणितीय संगणनाओं के बारे में जानेंगे।
मेट्रिसेस का जोड़
दो या अधिक मेट्रिसेस का जुड़ाव संभव है अगर मैट्रिस एक ही आयाम के हों। इसके अलावा दिए गए स्थान के अनुसार प्रत्येक तत्व का जोड़ शामिल है।
मैट्रिस कैसे काम करता है, यह समझने के लिए निम्नलिखित उदाहरण पर विचार करें -
$$ उदाहरण: A = \ start {bmatrix} 1 & 2 \\ 3 & 4 \ end {bmatrix} B = \ start {bmatrix} 5 और 6 \\ 7 & 8 \ अंत {bmatrix} \: फिर \ _ A + B = \ start {bmatrix} 1 + 5 & 2 + 6 \\ 3 + 7 और 4 + 8 \ अंत {bmatrix} = \ start {bmatrix} 6 & 8 \\ 10 & 12 \ end {bmatrix}}
मेट्रिसेस का घटाव
मेट्रिसेस का घटाव दो मैट्रिसेस के जोड़ के समान फैशन में संचालित होता है। उपयोगकर्ता दो मैट्रिक्स को घटा सकता है बशर्ते आयाम समान हों।
$$ उदाहरण: A- \ start {bmatrix} 1 & 2 \\ 3 & 4 \ end {bmatrix} B- \ start {bmatrix} 5 & 6 \\ 7 & 8 \ अंत {bmatrix} \: तत्कालीन \ _: AB - शुरू करें {bmatrix} 1-5 & 2-6 \\ 3-7 & 4-8 \ end {bmatrix} - \ start {bmatrix} -4 & -4 \\ - 4 & -4 \ end {bmatrix} $$
मैट्रिस का गुणन
दो मेट्रिसेस के लिए एक m * n और B p * q को गुणा करने के लिए, n के बराबर होना चाहिए p। परिणामी मैट्रिक्स है -
सी एम * क्यू
$$ A = \ start {bmatrix} 1 & 2 \\ 3 & 4 \ end {bmatrix} B = \ start {bmatrix} 5 और 6 \\ 7 & 8 \ अंत {bmatrix} $$
$$ c_ {11} = \ start {bmatrix} 1 & 2 \ end {bmatrix} \ start {bmatrix} 5 \\ 7 \ end {bmatrix} = 1 \ times5 + 2 \ times7 = 19 \ _ c_ {12} = \ start {bmatrix} 1 & 2 \ end {bmatrix} \ start {bmatrix} 6 \\ 8 \ अंत {bmatrix} = 1 \ times6 + 2 \ times8 = 22 $ $
$$ c_ {21} = \ start {bmatrix} 3 & 4 \ end {bmatrix} \ start {bmatrix} 5 \\ 7 \ end {bmatrix} = 3 \ times5 + 4 \ times7 = 43 \ _ c_ {22} = \ start {bmatrix} 3 & 4 \ end {bmatrix} \ start {bmatrix} 6 \\ 8 \ अंत {bmatrix} = 3 \ times6 + 4 \ times8 = 50 $ $
$ $ C = \ start {bmatrix} c_ {11} & c_ {12} \\ c_ {21} & c_ {22} \ end {bmatrix} = \ start {bmatrix} 19 & 22 \\ 43 और 50 \ अंत {} bmatrix $$
मैट्रिक्स का संक्रमण
मैट्रिक्स A, m * n का संक्रमण आमतौर पर AT (transpose) n * m द्वारा दर्शाया जाता है और स्तंभ वैक्टर को पंक्ति वैक्टर के रूप में स्थानांतरित करके प्राप्त किया जाता है।
$$ उदाहरण: A = \ start {bmatrix} 1 & 2 \\ 3 & 4 \ end {bmatrix} \: तत्पश्चात \ _ A ^ {T} \ start {bmatrix} 1 & 3 \\ 2 & 4 \ end { bmatrix} $$
वैक्टर के डॉट उत्पाद
आयाम n के किसी भी वेक्टर को मैट्रिक्स v = R ^ n * 1 के रूप में दर्शाया जा सकता है।
$$ v_ {1} = \ start {bmatrix} v_ {11} \\ v_ {12} \\ cdot \\\ cdot \\\ cdot \\ v_ {1n} \ end {bmatrix, v_ {2} = = \ start {bmatrix} v_ {21} \\ v_ {22} \\\ cdot \\\ cdot \\\ cdot \\ vdot {END 2 \ _n} \ end {bmatrix} $ $
दो वैक्टर का डॉट उत्पाद संगत घटकों के उत्पाद का योग है - समान आयाम के साथ घटक और के रूप में व्यक्त किया जा सकता है
$ $ v_ {1} \ cdot v_ {2} = v_1 ^ Tv_ {2} = v_2 ^ Tv_ {1} = v_ {11} v_ {21} + v_ {12} v_ {22 = + \ _ cdot + cdot + v_ {1n} v_ {2n} = \ displaystyle \ sum \ limit_ {k = 1} ^ n v_ {1k} v_ {2k} $ $
वैक्टर के डॉट उत्पाद का उदाहरण नीचे दिया गया है -
$$ उदाहरण: v_ {1} = \ start {bmatrix} 1 \\ 2 \\ 3 \ end {bmatrix} v_ {2} = \ start {bmatrix} 3 \\ 5 \\ - 1 \ end {bmatrix} v_ {1} \ cdot v_ {2} = v_1 ^ Tv_ {2} = 1 \ times3 + 2 \ times5-3 \ times1 = १० $