AI dengan Python - Pembelajaran yang Diawasi: Klasifikasi
Pada bab ini, kita akan fokus pada penerapan supervised learning - klasifikasi.
Teknik atau model klasifikasi berusaha mendapatkan kesimpulan dari nilai-nilai yang diamati. Dalam klasifikasi masalah, kami memiliki keluaran yang dikategorikan seperti "Hitam" atau "Putih" atau "Mengajar" dan "Non-Mengajar". Saat membangun model klasifikasi, kita perlu memiliki set data pelatihan yang berisi titik data dan label yang sesuai. Misalnya, jika kita ingin memeriksa apakah gambar itu mobil atau bukan. Untuk memeriksa ini, kita akan membuat set data pelatihan yang memiliki dua kelas yang terkait dengan "mobil" dan "tidak ada mobil". Kemudian kita perlu melatih model dengan menggunakan sampel pelatihan. Model klasifikasi terutama digunakan dalam pengenalan wajah, identifikasi spam, dll.
Langkah-langkah untuk Membangun Pengklasifikasi dengan Python
Untuk membangun pengklasifikasi dengan Python, kita akan menggunakan Python 3 dan Scikit-learn yang merupakan alat untuk pembelajaran mesin. Ikuti langkah-langkah ini untuk membuat pengklasifikasi dengan Python -
Langkah 1 - Impor Scikit-learn
Ini akan menjadi langkah pertama untuk membangun pengklasifikasi dengan Python. Pada langkah ini, kita akan menginstal paket Python bernama Scikit-learn yang merupakan salah satu modul pembelajaran mesin terbaik di Python. Perintah berikut akan membantu kami mengimpor paket -
Import SklearnLangkah 2 - Impor dataset Scikit-learn
Pada langkah ini, kita dapat mulai mengerjakan kumpulan data untuk model pembelajaran mesin kita. Di sini, kami akan menggunakanthe Database Diagnostik Kanker Payudara Wisconsin. Dataset mencakup berbagai informasi tentang tumor kanker payudara, serta label klasifikasimalignant atau benign. Dataset memiliki 569 kasus, atau data, pada 569 tumor dan mencakup informasi tentang 30 atribut, atau fitur, seperti radius tumor, tekstur, kehalusan, dan luas. Dengan bantuan perintah berikut, kita dapat mengimpor kumpulan data kanker payudara Scikit-learn -
from sklearn.datasets import load_breast_cancerSekarang, perintah berikut akan memuat dataset.
data = load_breast_cancer()Berikut adalah daftar kunci kamus penting -
- Nama label klasifikasi (target_names)
- Label sebenarnya (target)
- Nama atribut / fitur (feature_names)
- Atribut (data)
Sekarang, dengan bantuan perintah berikut, kita dapat membuat variabel baru untuk setiap kumpulan informasi penting dan menetapkan datanya. Dengan kata lain, kita dapat mengatur data dengan perintah berikut -
label_names = data['target_names']
labels = data['target']
feature_names = data['feature_names']
features = data['data']Sekarang, untuk membuatnya lebih jelas kita dapat mencetak label kelas, label contoh data pertama, nama fitur kita dan nilai fitur dengan bantuan perintah berikut -
print(label_names)Perintah di atas akan mencetak nama kelas yang masing-masing ganas dan jinak. Itu ditunjukkan sebagai output di bawah ini -
['malignant' 'benign']Sekarang, perintah di bawah ini akan menunjukkan bahwa mereka dipetakan ke nilai biner 0 dan 1. Di sini 0 mewakili kanker ganas dan 1 mewakili kanker jinak. Anda akan menerima output berikut -
print(labels[0])
0Dua perintah yang diberikan di bawah ini akan menghasilkan nama fitur dan nilai fitur.
print(feature_names[0])
mean radius
print(features[0])
[ 1.79900000e+01 1.03800000e+01 1.22800000e+02 1.00100000e+03
1.18400000e-01 2.77600000e-01 3.00100000e-01 1.47100000e-01
2.41900000e-01 7.87100000e-02 1.09500000e+00 9.05300000e-01
8.58900000e+00 1.53400000e+02 6.39900000e-03 4.90400000e-02
5.37300000e-02 1.58700000e-02 3.00300000e-02 6.19300000e-03
2.53800000e+01 1.73300000e+01 1.84600000e+02 2.01900000e+03
1.62200000e-01 6.65600000e-01 7.11900000e-01 2.65400000e-01
4.60100000e-01 1.18900000e-01]Dari keluaran di atas terlihat bahwa contoh data pertama adalah tumor ganas yang radiusnya 1.7990000e + 01.
Langkah 3 - Mengatur data menjadi beberapa set
Pada langkah ini kita akan membagi data kita menjadi dua bagian yaitu training set dan test set. Memisahkan data menjadi set ini sangat penting karena kita harus menguji model kita pada data yang tidak terlihat. Untuk membagi data menjadi beberapa set, sklearn memiliki fungsi yang disebuttrain_test_split()fungsi. Dengan bantuan perintah berikut, kita dapat membagi data dalam set ini -
from sklearn.model_selection import train_test_splitPerintah di atas akan mengimpor file train_test_splitfungsi dari sklearn dan perintah di bawah ini akan membagi data menjadi data pelatihan dan pengujian. Dalam contoh yang diberikan di bawah ini, kami menggunakan 40% data untuk pengujian dan data yang tersisa akan digunakan untuk melatih model.
train, test, train_labels, test_labels = train_test_split(features,labels,test_size = 0.40, random_state = 42)Langkah 4 - Membangun model
Pada langkah ini, kami akan membangun model kami. Kami akan menggunakan algoritma Naïve Bayes untuk membangun model. Perintah berikut dapat digunakan untuk membangun model -
from sklearn.naive_bayes import GaussianNBPerintah di atas akan mengimpor modul GaussianNB. Sekarang, perintah berikut akan membantu Anda menginisialisasi model.
gnb = GaussianNB()Kami akan melatih model dengan menyesuaikannya dengan data dengan menggunakan gnb.fit ().
model = gnb.fit(train, train_labels)Langkah 5 - Mengevaluasi model dan akurasinya
Pada langkah ini, kami akan mengevaluasi model dengan membuat prediksi pada data pengujian kami. Kemudian kita akan mengetahui akurasinya juga. Untuk membuat prediksi, kita akan menggunakan fungsi predict (). Perintah berikut akan membantu Anda melakukan ini -
preds = gnb.predict(test)
print(preds)
[1 0 0 1 1 0 0 0 1 1 1 0 1 0 1 0 1 1 1 0 1 1 0 1 1 1 1 1 1
0 1 1 1 1 1 1 0 1 0 1 1 0 1 1 1 1 1 1 1 1 0 0 1 1 1 1 1 0
0 1 1 0 0 1 1 1 0 0 1 1 0 0 1 0 1 1 1 1 1 1 0 1 1 0 0 0 0
0 1 1 1 1 1 1 1 1 0 0 1 0 0 1 0 0 1 1 1 0 1 1 0 1 1 0 0 0
1 1 1 0 0 1 1 0 1 0 0 1 1 0 0 0 1 1 1 0 1 1 0 0 1 0 1 1 0
1 0 0 1 1 1 1 1 1 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 0
1 1 0 1 1 1 1 1 1 0 0 0 1 1 0 1 0 1 1 1 1 0 1 1 0 1 1 1 0
1 0 0 1 1 1 1 1 1 1 1 0 1 1 1 1 1 0 1 0 0 1 1 0 1]Seri 0 dan 1 di atas adalah nilai prediksi untuk kelas tumor - ganas dan jinak.
Sekarang, dengan membandingkan dua array yaitu test_labels dan preds, kami dapat mengetahui keakuratan model kami. Kami akan menggunakanaccuracy_score()berfungsi untuk menentukan akurasi. Pertimbangkan perintah berikut untuk ini -
from sklearn.metrics import accuracy_score
print(accuracy_score(test_labels,preds))
0.951754385965Hasil penelitian menunjukkan bahwa pengklasifikasi NaïveBayes akurat 95.17%.
Dengan cara ini, dengan bantuan langkah-langkah di atas kita dapat membangun pengklasifikasi kita dengan Python.
Membangun Pengklasifikasi dengan Python
Di bagian ini, kita akan belajar cara membuat pengklasifikasi dengan Python.
Penggolong Naïve Bayes
Naïve Bayes adalah teknik klasifikasi yang digunakan untuk membangun pengklasifikasi menggunakan teorema Bayes. Asumsinya adalah bahwa prediktor bersifat independen. Dengan kata sederhana, ini mengasumsikan bahwa keberadaan fitur tertentu di kelas tidak terkait dengan keberadaan fitur lainnya. Untuk membuat pengklasifikasi Naïve Bayes, kita perlu menggunakan pustaka python yang disebut scikit learn. Ada tiga jenis model Naïve Bayes yang diberi namaGaussian, Multinomial and Bernoulli di bawah paket belajar scikit.
Untuk membuat model pengklasifikasi pembelajaran mesin Naïve Bayes, kita membutuhkan yang berikut & minus
Himpunan data
Kami akan menggunakan kumpulan data bernama Breast Cancer Wisconsin Diagnostic Database. Dataset mencakup berbagai informasi tentang tumor kanker payudara, serta label klasifikasimalignant atau benign. Dataset memiliki 569 kasus, atau data, pada 569 tumor dan mencakup informasi tentang 30 atribut, atau fitur, seperti radius tumor, tekstur, kehalusan, dan luas. Kami dapat mengimpor dataset ini dari paket sklearn.
Model Naïve Bayes
Untuk membuat pengklasifikasi Naïve Bayes, kita membutuhkan model Naïve Bayes. Seperti yang diceritakan sebelumnya, ada tiga jenis model Naïve Bayes yang diberi namaGaussian, Multinomial dan Bernoullidi bawah paket belajar scikit. Di sini, pada contoh berikut kita akan menggunakan model Gaussian Naïve Bayes.
Dengan menggunakan cara di atas, kita akan membuat model pembelajaran mesin Naïve Bayes untuk menggunakan informasi tumor untuk memprediksi apakah tumor itu ganas atau jinak.
Untuk memulainya, kita perlu menginstal modul sklearn. Itu dapat dilakukan dengan bantuan perintah berikut -
Import SklearnSekarang, kita perlu mengimpor dataset bernama Breast Cancer Wisconsin Diagnostic Database.
from sklearn.datasets import load_breast_cancerSekarang, perintah berikut akan memuat dataset.
data = load_breast_cancer()Data dapat diatur sebagai berikut -
label_names = data['target_names']
labels = data['target']
feature_names = data['feature_names']
features = data['data']Sekarang, untuk membuatnya lebih jelas kita dapat mencetak label kelas, label contoh data pertama, nama fitur kita dan nilai fitur dengan bantuan perintah berikut -
print(label_names)Perintah di atas akan mencetak nama kelas yang masing-masing ganas dan jinak. Itu ditunjukkan sebagai output di bawah ini -
['malignant' 'benign']Sekarang, perintah yang diberikan di bawah ini akan menunjukkan bahwa mereka dipetakan ke nilai biner 0 dan 1. Di sini 0 mewakili kanker ganas dan 1 mewakili kanker jinak. Itu ditunjukkan sebagai output di bawah ini -
print(labels[0])
0Dua perintah berikut akan menghasilkan nama fitur dan nilai fitur.
print(feature_names[0])
mean radius
print(features[0])
[ 1.79900000e+01 1.03800000e+01 1.22800000e+02 1.00100000e+03
1.18400000e-01 2.77600000e-01 3.00100000e-01 1.47100000e-01
2.41900000e-01 7.87100000e-02 1.09500000e+00 9.05300000e-01
8.58900000e+00 1.53400000e+02 6.39900000e-03 4.90400000e-02
5.37300000e-02 1.58700000e-02 3.00300000e-02 6.19300000e-03
2.53800000e+01 1.73300000e+01 1.84600000e+02 2.01900000e+03
1.62200000e-01 6.65600000e-01 7.11900000e-01 2.65400000e-01
4.60100000e-01 1.18900000e-01]Dari keluaran di atas terlihat bahwa contoh data pertama adalah tumor ganas dengan radius utama 1.7990000e + 01.
Untuk menguji model kita pada data yang tidak terlihat, kita perlu membagi data kita menjadi data pelatihan dan pengujian. Itu dapat dilakukan dengan bantuan kode berikut -
from sklearn.model_selection import train_test_splitPerintah di atas akan mengimpor file train_test_splitfungsi dari sklearn dan perintah di bawah ini akan membagi data menjadi data pelatihan dan pengujian. Dalam contoh di bawah ini, kami menggunakan 40% data untuk pengujian dan remining data akan digunakan untuk melatih model.
train, test, train_labels, test_labels =
train_test_split(features,labels,test_size = 0.40, random_state = 42)Sekarang, kami membangun model dengan perintah berikut -
from sklearn.naive_bayes import GaussianNBPerintah di atas akan mengimpor file GaussianNBmodul. Sekarang, dengan perintah yang diberikan di bawah ini, kita perlu menginisialisasi model.
gnb = GaussianNB()Kami akan melatih model dengan menyesuaikannya dengan data dengan menggunakan gnb.fit().
model = gnb.fit(train, train_labels)Sekarang evaluasi model dengan membuat prediksi pada data uji dan dapat dilakukan sebagai berikut:
preds = gnb.predict(test)
print(preds)
[1 0 0 1 1 0 0 0 1 1 1 0 1 0 1 0 1 1 1 0 1 1 0 1 1 1 1 1 1
0 1 1 1 1 1 1 0 1 0 1 1 0 1 1 1 1 1 1 1 1 0 0 1 1 1 1 1 0
0 1 1 0 0 1 1 1 0 0 1 1 0 0 1 0 1 1 1 1 1 1 0 1 1 0 0 0 0
0 1 1 1 1 1 1 1 1 0 0 1 0 0 1 0 0 1 1 1 0 1 1 0 1 1 0 0 0
1 1 1 0 0 1 1 0 1 0 0 1 1 0 0 0 1 1 1 0 1 1 0 0 1 0 1 1 0
1 0 0 1 1 1 1 1 1 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 0
1 1 0 1 1 1 1 1 1 0 0 0 1 1 0 1 0 1 1 1 1 0 1 1 0 1 1 1 0
1 0 0 1 1 1 1 1 1 1 1 0 1 1 1 1 1 0 1 0 0 1 1 0 1]Rangkaian 0s dan 1s di atas adalah nilai prediksi untuk kelas tumor yaitu ganas dan jinak.
Sekarang, dengan membandingkan dua array yaitu test_labels dan preds, kami dapat mengetahui keakuratan model kami. Kami akan menggunakanaccuracy_score()berfungsi untuk menentukan akurasi. Pertimbangkan perintah berikut -
from sklearn.metrics import accuracy_score
print(accuracy_score(test_labels,preds))
0.951754385965Hasil penelitian menunjukkan bahwa pengklasifikasi NaïveBayes akurat 95.17%.
Itu adalah pengklasifikasi pembelajaran mesin berdasarkan model Naïve Bayse Gaussian.
Mendukung Mesin Vektor (SVM)
Pada dasarnya, Support vector machine (SVM) adalah algoritma pembelajaran mesin yang diawasi yang dapat digunakan untuk regresi dan klasifikasi. Konsep utama SVM adalah memplot setiap item data sebagai titik dalam ruang berdimensi n dengan nilai setiap fitur menjadi nilai koordinat tertentu. Di sini akan menjadi fitur yang akan kami miliki. Berikut adalah representasi grafis sederhana untuk memahami konsep SVM -
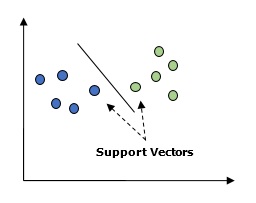
Pada diagram di atas, kami memiliki dua fitur. Oleh karena itu, pertama-tama kita perlu memplot kedua variabel ini dalam ruang dua dimensi di mana setiap titik memiliki dua koordinat, yang disebut vektor pendukung. Garis membagi data menjadi dua kelompok rahasia yang berbeda. Baris ini akan menjadi pengklasifikasi.
Di sini, kita akan membuat pengklasifikasi SVM dengan menggunakan scikit-learn dan dataset iris. Perpustakaan Scikitlearn memiliki ekstensisklearn.svmmodul dan menyediakan sklearn.svm.svc untuk klasifikasi. Pengklasifikasi SVM untuk memprediksi kelas tanaman iris berdasarkan 4 fitur ditampilkan di bawah ini.
Himpunan data
Kami akan menggunakan dataset iris yang berisi 3 kelas masing-masing 50 instance, di mana setiap kelas mengacu pada jenis tanaman iris. Setiap tanaman memiliki empat ciri yaitu panjang sepal, lebar sepal, panjang kelopak, dan lebar kelopak. Pengklasifikasi SVM untuk memprediksi kelas tanaman iris berdasarkan 4 fitur ditampilkan di bawah ini.
Inti
Ini adalah teknik yang digunakan oleh SVM. Pada dasarnya ini adalah fungsi yang mengambil ruang masukan berdimensi rendah dan mengubahnya menjadi ruang berdimensi lebih tinggi. Ini mengubah masalah yang tidak dapat dipisahkan menjadi masalah yang dapat dipisahkan. Fungsi kernel dapat berupa salah satu di antara linear, polinomial, rbf dan sigmoid. Dalam contoh ini, kami akan menggunakan kernel linier.
Mari kita sekarang mengimpor paket-paket berikut -
import pandas as pd
import numpy as np
from sklearn import svm, datasets
import matplotlib.pyplot as pltSekarang, muat data masukan -
iris = datasets.load_iris()Kami mengambil dua fitur pertama -
X = iris.data[:, :2]
y = iris.targetKami akan memplot batas mesin vektor dukungan dengan data asli. Kami membuat mesh untuk plot.
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
h = (x_max / x_min)/100
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
np.arange(y_min, y_max, h))
X_plot = np.c_[xx.ravel(), yy.ravel()]Kita perlu memberikan nilai parameter regularisasi.
C = 1.0Kita perlu membuat objek pengklasifikasi SVM.
Svc_classifier = svm_classifier.SVC(kernel='linear',
C=C, decision_function_shape = 'ovr').fit(X, y)
Z = svc_classifier.predict(X_plot)
Z = Z.reshape(xx.shape)
plt.figure(figsize = (15, 5))
plt.subplot(121)
plt.contourf(xx, yy, Z, cmap = plt.cm.tab10, alpha = 0.3)
plt.scatter(X[:, 0], X[:, 1], c = y, cmap = plt.cm.Set1)
plt.xlabel('Sepal length')
plt.ylabel('Sepal width')
plt.xlim(xx.min(), xx.max())
plt.title('SVC with linear kernel')
Regresi logistik
Pada dasarnya, model regresi logistik adalah salah satu anggota keluarga algoritma klasifikasi terbimbing. Regresi logistik mengukur hubungan antara variabel dependen dan variabel independen dengan memperkirakan probabilitas menggunakan fungsi logistik.
Di sini, jika kita berbicara tentang variabel dependen dan variabel independen maka variabel dependen adalah variabel kelas sasaran yang akan kita prediksi dan di sisi lain variabel independen adalah fitur yang akan kita gunakan untuk memprediksi kelas sasaran.
Dalam regresi logistik, mengestimasi probabilitas berarti memprediksi kemungkinan terjadinya peristiwa tersebut. Misal, pemilik toko ingin memprediksi pelanggan yang masuk ke toko akan membeli play station (misalnya) atau tidak. Akan ada banyak fitur pelanggan - jenis kelamin, usia, dll. Yang akan diamati oleh penjaga toko untuk memprediksi kemungkinan terjadinya, yaitu membeli play station atau tidak. Fungsi logistik merupakan kurva sigmoid yang digunakan untuk membangun fungsi dengan berbagai parameter.
Prasyarat
Sebelum membangun pengklasifikasi menggunakan regresi logistik, kita perlu menginstal paket Tkinter di sistem kita. Itu dapat diinstal darihttps://docs.python.org/2/library/tkinter.html.
Sekarang, dengan bantuan kode yang diberikan di bawah ini, kita dapat membuat pengklasifikasi menggunakan regresi logistik -
Pertama, kami akan mengimpor beberapa paket -
import numpy as np
from sklearn import linear_model
import matplotlib.pyplot as pltSekarang, kita perlu menentukan data sampel yang dapat dilakukan sebagai berikut -
X = np.array([[2, 4.8], [2.9, 4.7], [2.5, 5], [3.2, 5.5], [6, 5], [7.6, 4],
[3.2, 0.9], [2.9, 1.9],[2.4, 3.5], [0.5, 3.4], [1, 4], [0.9, 5.9]])
y = np.array([0, 0, 0, 1, 1, 1, 2, 2, 2, 3, 3, 3])Selanjutnya, kita perlu membuat pengklasifikasi regresi logistik, yang dapat dilakukan sebagai berikut -
Classifier_LR = linear_model.LogisticRegression(solver = 'liblinear', C = 75)Terakhir, kita perlu melatih pengklasifikasi ini -
Classifier_LR.fit(X, y)Sekarang, bagaimana kita dapat memvisualisasikan hasilnya? Itu bisa dilakukan dengan membuat fungsi bernama Logistic_visualize () -
Def Logistic_visualize(Classifier_LR, X, y):
min_x, max_x = X[:, 0].min() - 1.0, X[:, 0].max() + 1.0
min_y, max_y = X[:, 1].min() - 1.0, X[:, 1].max() + 1.0Pada baris di atas, kami mendefinisikan nilai minimum dan maksimum X dan Y untuk digunakan dalam grid mesh. Selain itu, kami akan menentukan ukuran langkah untuk memplot grid mesh.
mesh_step_size = 0.02Mari kita tentukan grid mesh dari nilai X dan Y sebagai berikut -
x_vals, y_vals = np.meshgrid(np.arange(min_x, max_x, mesh_step_size),
np.arange(min_y, max_y, mesh_step_size))Dengan bantuan kode berikut, kita dapat menjalankan pengklasifikasi pada grid mesh -
output = classifier.predict(np.c_[x_vals.ravel(), y_vals.ravel()])
output = output.reshape(x_vals.shape)
plt.figure()
plt.pcolormesh(x_vals, y_vals, output, cmap = plt.cm.gray)
plt.scatter(X[:, 0], X[:, 1], c = y, s = 75, edgecolors = 'black',
linewidth=1, cmap = plt.cm.Paired)Baris kode berikut akan menentukan batas plot
plt.xlim(x_vals.min(), x_vals.max())
plt.ylim(y_vals.min(), y_vals.max())
plt.xticks((np.arange(int(X[:, 0].min() - 1), int(X[:, 0].max() + 1), 1.0)))
plt.yticks((np.arange(int(X[:, 1].min() - 1), int(X[:, 1].max() + 1), 1.0)))
plt.show()Sekarang, setelah menjalankan kode kita akan mendapatkan keluaran berikut, pengklasifikasi regresi logistik -

Pengklasifikasi Pohon Keputusan
Pohon keputusan pada dasarnya adalah diagram alur pohon biner di mana setiap node membagi kelompok pengamatan menurut beberapa variabel fitur.
Di sini, kami sedang membangun pengklasifikasi Pohon Keputusan untuk memprediksi pria atau wanita. Kami akan mengambil kumpulan data yang sangat kecil yang memiliki 19 sampel. Sampel ini akan terdiri dari dua fitur - 'tinggi' dan 'panjang rambut'.
Prasyarat
Untuk membangun pengklasifikasi berikut, kita perlu menginstal pydotplus dan graphviz. Pada dasarnya, graphviz adalah alat untuk menggambar grafik menggunakan file titik danpydotplusadalah modul untuk bahasa Dot Graphviz. Itu dapat diinstal dengan manajer paket atau pip.
Sekarang, kita dapat membangun pengklasifikasi pohon keputusan dengan bantuan kode Python berikut -
Untuk memulainya, mari kita impor beberapa perpustakaan penting sebagai berikut -
import pydotplus
from sklearn import tree
from sklearn.datasets import load_iris
from sklearn.metrics import classification_report
from sklearn import cross_validation
import collectionsSekarang, kita perlu menyediakan dataset sebagai berikut -
X = [[165,19],[175,32],[136,35],[174,65],[141,28],[176,15],[131,32],
[166,6],[128,32],[179,10],[136,34],[186,2],[126,25],[176,28],[112,38],
[169,9],[171,36],[116,25],[196,25]]
Y = ['Man','Woman','Woman','Man','Woman','Man','Woman','Man','Woman',
'Man','Woman','Man','Woman','Woman','Woman','Man','Woman','Woman','Man']
data_feature_names = ['height','length of hair']
X_train, X_test, Y_train, Y_test = cross_validation.train_test_split
(X, Y, test_size=0.40, random_state=5)Setelah memberikan dataset, kita perlu menyesuaikan model yang dapat dilakukan sebagai berikut -
clf = tree.DecisionTreeClassifier()
clf = clf.fit(X,Y)Prediksi dapat dilakukan dengan bantuan kode Python berikut -
prediction = clf.predict([[133,37]])
print(prediction)Kita dapat memvisualisasikan pohon keputusan dengan bantuan kode Python berikut -
dot_data = tree.export_graphviz(clf,feature_names = data_feature_names,
out_file = None,filled = True,rounded = True)
graph = pydotplus.graph_from_dot_data(dot_data)
colors = ('orange', 'yellow')
edges = collections.defaultdict(list)
for edge in graph.get_edge_list():
edges[edge.get_source()].append(int(edge.get_destination()))
for edge in edges: edges[edge].sort()
for i in range(2):dest = graph.get_node(str(edges[edge][i]))[0]
dest.set_fillcolor(colors[i])
graph.write_png('Decisiontree16.png')Ini akan memberikan prediksi untuk kode di atas sebagai [‘Woman’] dan buat pohon keputusan berikut -

Kita dapat mengubah nilai fitur dalam prediksi untuk mengujinya.
Pengklasifikasi Hutan Acak
Seperti yang kita ketahui bahwa metode ensemble adalah metode yang menggabungkan model pembelajaran mesin menjadi model pembelajaran mesin yang lebih canggih. Random Forest, kumpulan pohon keputusan, adalah salah satunya. Ini lebih baik daripada pohon keputusan tunggal karena dengan tetap mempertahankan kekuatan prediksi, hal itu dapat mengurangi penyesuaian berlebih dengan membuat rata-rata hasil. Di sini, kita akan mengimplementasikan model hutan acak pada set data scikit learn kanker.
Impor paket yang diperlukan -
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_breast_cancer
cancer = load_breast_cancer()
import matplotlib.pyplot as plt
import numpy as npSekarang, kita perlu menyediakan dataset yang bisa dilakukan sebagai berikut & minus
cancer = load_breast_cancer()
X_train, X_test, y_train,
y_test = train_test_split(cancer.data, cancer.target, random_state = 0)Setelah memberikan dataset, kita perlu menyesuaikan model yang dapat dilakukan sebagai berikut -
forest = RandomForestClassifier(n_estimators = 50, random_state = 0)
forest.fit(X_train,y_train)Sekarang, dapatkan akurasi subset training dan testing: jika kita akan menambah jumlah estimator maka akurasi subset testing juga akan meningkat.
print('Accuracy on the training subset:(:.3f)',format(forest.score(X_train,y_train)))
print('Accuracy on the training subset:(:.3f)',format(forest.score(X_test,y_test)))Keluaran
Accuracy on the training subset:(:.3f) 1.0
Accuracy on the training subset:(:.3f) 0.965034965034965Sekarang, seperti pohon keputusan, hutan acak memiliki feature_importancemodul yang akan memberikan tampilan bobot fitur yang lebih baik daripada pohon keputusan. Itu dapat di plot dan divisualisasikan sebagai berikut -
n_features = cancer.data.shape[1]
plt.barh(range(n_features),forest.feature_importances_, align='center')
plt.yticks(np.arange(n_features),cancer.feature_names)
plt.xlabel('Feature Importance')
plt.ylabel('Feature')
plt.show()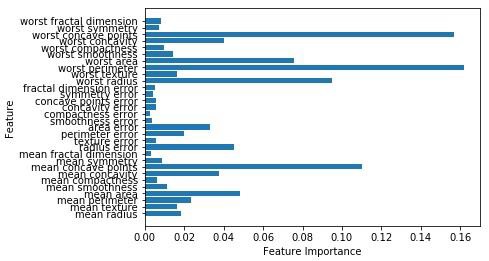
Performa pengklasifikasi
Setelah menerapkan algoritma pembelajaran mesin, kita perlu mengetahui seberapa efektif model tersebut. Kriteria untuk mengukur keefektifan dapat didasarkan pada kumpulan data dan metrik. Untuk mengevaluasi algoritme pembelajaran mesin yang berbeda, kita dapat menggunakan metrik kinerja yang berbeda. Misalnya, jika pengklasifikasi digunakan untuk membedakan gambar dari objek yang berbeda, kita dapat menggunakan metrik kinerja klasifikasi seperti akurasi rata-rata, AUC, dll. Dalam satu atau lain hal, metrik yang kita pilih untuk mengevaluasi model pembelajaran mesin kita adalah sangat penting karena pilihan metrik memengaruhi bagaimana performa algoritma pembelajaran mesin diukur dan dibandingkan. Berikut adalah beberapa metrik -
Confusion Matrix
Pada dasarnya ini digunakan untuk masalah klasifikasi dimana keluarannya bisa dari dua atau lebih jenis kelas. Ini adalah cara termudah untuk mengukur kinerja pengklasifikasi. Matriks konfusi pada dasarnya adalah tabel dengan dua dimensi yaitu “Aktual” dan “Diprediksi”. Kedua dimensi tersebut memiliki “True Positives (TP)”, “True Negatives (TN)”, “False Positives (FP)”, “False Negatives (FN)”.
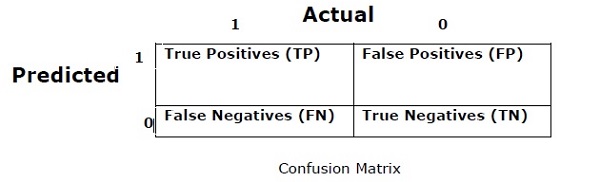
Dalam matriks konfusi di atas, 1 untuk kelas positif dan 0 untuk kelas negatif.
Berikut adalah istilah yang terkait dengan matriks Kebingungan -
True Positives − TP adalah kasus ketika kelas titik data aktual adalah 1 dan prediksi juga 1.
True Negatives − TN adalah kasus ketika kelas aktual dari titik data adalah 0 dan prediksi juga 0.
False Positives − FP adalah kasus ketika kelas sebenarnya dari titik data adalah 0 dan prediksi juga 1.
False Negatives − FN adalah kasus ketika kelas aktual dari titik data adalah 1 dan prediksi juga 0.
Ketepatan
Matriks konfusi itu sendiri bukanlah ukuran kinerja tetapi hampir semua matriks kinerja didasarkan pada matriks konfusi. Salah satunya adalah akurasi. Dalam masalah klasifikasi, ini dapat didefinisikan sebagai jumlah prediksi benar yang dibuat oleh model atas semua jenis prediksi yang dibuat. Rumus untuk menghitung akurasinya adalah sebagai berikut -
$$ Akurasi = \ frac {TP + TN} {TP + FP + FN + TN} $$
Presisi
Ini sebagian besar digunakan dalam pengambilan dokumen. Ini dapat didefinisikan sebagai berapa banyak dari dokumen yang dikembalikan benar. Berikut adalah rumus untuk menghitung presisi -
$$ Presisi = \ frac {TP} {TP + FP} $$
Ingat atau Sensitivitas
Ini dapat didefinisikan sebagai berapa banyak hal positif yang dihasilkan model. Berikut adalah rumus untuk menghitung recall / sensitivitas model -
$$ Perolehan = \ frac {TP} {TP + FN} $$
Kekhususan
Ini dapat didefinisikan sebagai berapa banyak negatif yang dikembalikan model. Ini sangat berlawanan dengan mengingat. Berikut rumus untuk menghitung kekhususan model -
$$ Kekhususan = \ frac {TN} {TN + FP} $$
Masalah Ketidakseimbangan Kelas
Ketidakseimbangan kelas adalah skenario di mana jumlah pengamatan milik satu kelas secara signifikan lebih rendah daripada yang dimiliki kelas lainnya. Misalnya, masalah ini menonjol dalam skenario di mana kita perlu mengidentifikasi penyakit langka, transaksi curang di bank, dll.
Contoh kelas yang tidak seimbang
Mari kita pertimbangkan contoh kumpulan data deteksi penipuan untuk memahami konsep kelas yang tidak seimbang -
Total observations = 5000
Fraudulent Observations = 50
Non-Fraudulent Observations = 4950
Event Rate = 1%Larutan
Balancing the classes’bertindak sebagai solusi untuk kelas yang tidak seimbang. Tujuan utama penyeimbangan kelas adalah untuk meningkatkan frekuensi kelas minoritas atau menurunkan frekuensi kelas mayoritas. Berikut adalah pendekatan untuk mengatasi masalah ketidakseimbangan kelas -
Pengambilan Sampel Ulang
Pengambilan sampel ulang adalah serangkaian metode yang digunakan untuk merekonstruksi kumpulan data sampel - baik set pelatihan maupun set pengujian. Re-sampling dilakukan untuk meningkatkan akurasi model. Berikut adalah beberapa teknik pengambilan sampel ulang -
Random Under-Sampling- Teknik ini bertujuan untuk menyeimbangkan distribusi kelas dengan menghilangkan contoh kelas mayoritas secara acak. Ini dilakukan sampai instance kelas mayoritas dan minoritas seimbang.
Total observations = 5000
Fraudulent Observations = 50
Non-Fraudulent Observations = 4950
Event Rate = 1%Dalam hal ini, kami mengambil 10% sampel tanpa penggantian dari contoh non-penipuan dan kemudian menggabungkannya dengan contoh penipuan -
Pengamatan tidak curang setelah random under sampling = 10% dari 4950 = 495
Total observasi setelah digabungkan dengan observasi curang = 50 + 495 = 545
Karenanya, rasio peristiwa untuk set data baru setelah pengambilan sampel = 9%
Keuntungan utama dari teknik ini adalah dapat mengurangi waktu pengoperasian dan meningkatkan penyimpanan. Namun di sisi lain, dapat membuang informasi yang berguna sekaligus mengurangi jumlah sampel data latih.
Random Over-Sampling - Teknik ini bertujuan untuk menyeimbangkan distribusi kelas dengan meningkatkan jumlah instance di kelas minoritas dengan mereplikasi mereka.
Total observations = 5000
Fraudulent Observations = 50
Non-Fraudulent Observations = 4950
Event Rate = 1%Jika kita mereplikasi 50 pengamatan curang sebanyak 30 kali maka pengamatan curang setelah mereplikasi pengamatan kelas minoritas akan menjadi 1500. Dan kemudian total pengamatan dalam data baru setelah oversampling akan menjadi 4950 + 1500 = 6450. Oleh karena itu tingkat kejadian untuk kumpulan data baru akan menjadi 1500/6450 = 23%.
Keuntungan utama dari metode ini adalah tidak ada kehilangan informasi yang berguna. Namun di sisi lain, kemungkinan over-fitting meningkat karena mereplikasi peristiwa kelas minoritas.
Teknik Ensemble
Metodologi ini pada dasarnya digunakan untuk memodifikasi algoritma klasifikasi yang ada agar sesuai untuk kumpulan data yang tidak seimbang. Dalam pendekatan ini kami membuat beberapa pengklasifikasi dua tahap dari data asli dan kemudian menggabungkan prediksinya. Pengklasifikasi hutan acak adalah contoh pengklasifikasi berbasis ansambel.