AI - Algoritma Pencarian Populer

Pencarian adalah teknik universal pemecahan masalah dalam AI. Ada beberapa game pemain tunggal seperti game ubin, Sudoku, teka-teki silang, dll. Algoritme pencarian membantu Anda mencari posisi tertentu dalam game tersebut.

Masalah Pathfinding Agen Tunggal

Permainan seperti 3X3 delapan ubin, 4X4 lima belas ubin, dan 5X5 dua puluh empat ubin teka-teki adalah tantangan menemukan jalur agen tunggal. Mereka terdiri dari matriks ubin dengan ubin kosong. Pemain diharuskan untuk mengatur ubin dengan menggeser ubin baik secara vertikal maupun horizontal ke dalam ruang kosong dengan tujuan mencapai beberapa tujuan.

Contoh lain dari masalah pathfinding agen tunggal adalah Travelling Salesman Problem, Rubik's Cube, dan Theorem Proving.

Istilah Pencarian

Problem Space- Ini adalah lingkungan tempat pencarian dilakukan. (Seperangkat negara bagian dan serangkaian operator untuk mengubah keadaan tersebut)
Problem Instance - Ini adalah keadaan awal + keadaan Tujuan.
Problem Space Graph- Ini mewakili keadaan masalah. Status ditunjukkan oleh node dan operator ditunjukkan oleh tepi.
Depth of a problem - Panjang jalur terpendek atau urutan terpendek operator dari Status Awal ke status tujuan.
Space Complexity - Jumlah maksimum node yang disimpan di memori.
Time Complexity - Jumlah maksimum node yang dibuat.
Admissibility - Properti algoritme untuk selalu menemukan solusi optimal.
Branching Factor - Jumlah rata-rata node anak dalam grafik ruang masalah.
Depth - Panjang jalur terpendek dari keadaan awal ke keadaan tujuan.

Strategi Pencarian Brute-Force

Mereka paling sederhana, karena mereka tidak membutuhkan pengetahuan khusus domain. Mereka bekerja dengan baik dengan sejumlah kecil kemungkinan negara bagian.

Persyaratan -

Deskripsi negara bagian
Satu set operator yang valid
Keadaan awal
Deskripsi status tujuan

Pencarian Luas-Pertama

Ini dimulai dari simpul akar, menjelajahi simpul tetangga terlebih dahulu dan bergerak menuju tetangga tingkat berikutnya. Ini menghasilkan satu pohon pada satu waktu sampai solusinya ditemukan. Ini dapat diimplementasikan menggunakan struktur data antrian FIFO. Metode ini menyediakan jalur terpendek menuju solusi.

Jika branching factor(jumlah rata-rata node anak untuk node tertentu) = b dan kedalaman = d, lalu jumlah node pada level d = b ^d .

Jumlah total node yang dibuat dalam kasus terburuk adalah b + b ² + b ³ +… + b ^d .

Disadvantage- Karena setiap tingkat node disimpan untuk membuat yang berikutnya, ini menghabiskan banyak ruang memori. Persyaratan ruang untuk menyimpan node bersifat eksponensial.

Kompleksitasnya bergantung pada jumlah node. Itu dapat memeriksa node duplikat.

Pencarian Kedalaman-Pertama

Ini diimplementasikan dalam rekursi dengan struktur data tumpukan LIFO. Ini membuat kumpulan node yang sama dengan metode Breadth-First, hanya dalam urutan yang berbeda.

Karena node pada jalur tunggal disimpan di setiap iterasi dari akar ke node daun, persyaratan ruang untuk menyimpan node adalah linier. Dengan faktor percabangan b dan kedalaman sebagai m , ruang penyimpanannya adalah bm.

Disadvantage- Algoritma ini tidak boleh berhenti dan terus berjalan tanpa batas di satu jalur. Solusi untuk masalah ini adalah memilih kedalaman potong. Jika cut-off yang ideal adalah d , dan jika cut-off yang dipilih lebih kecil dari d , maka algoritma ini mungkin gagal. Jika cut-off yang dipilih lebih dari d , maka waktu eksekusi bertambah.

Kompleksitasnya bergantung pada jumlah jalur. Itu tidak dapat memeriksa node duplikat.

Pencarian dua arah

Ini mencari maju dari keadaan awal dan mundur dari keadaan tujuan sampai keduanya bertemu untuk mengidentifikasi keadaan bersama.

Jalur dari keadaan awal digabungkan dengan jalur terbalik dari keadaan tujuan. Setiap pencarian dilakukan hanya sampai setengah dari total jalur.

Pencarian Biaya Seragam

Penyortiran dilakukan dalam meningkatkan biaya jalur ke node. Itu selalu memperluas node biaya terendah. Ini identik dengan pencarian Breadth First jika setiap transisi memiliki biaya yang sama.

Ini mengeksplorasi jalur dalam urutan peningkatan biaya.

Disadvantage- Bisa ada beberapa jalur panjang dengan biaya ≤ C *. Pencarian Uniform Cost harus mengeksplorasi semuanya.

Iterative Deepening Depth-First Search

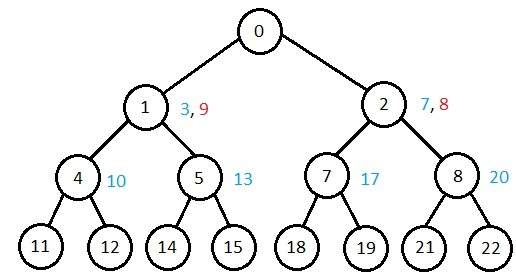
Ini melakukan pencarian kedalaman-pertama ke level 1, memulai kembali, mengeksekusi pencarian kedalaman-pertama lengkap ke level 2, dan berlanjut sedemikian rupa sampai solusi ditemukan.

Itu tidak pernah membuat node sampai semua node yang lebih rendah dibuat. Ini hanya menyimpan setumpuk node. Algoritme berakhir ketika menemukan solusi di kedalaman d . Jumlah node yang dibuat pada kedalaman d adalah b ^d dan pada kedalaman d-1 adalah b ^d-1.

Perbandingan Berbagai Kompleksitas Algoritma

Mari kita lihat performa algoritma berdasarkan berbagai kriteria -

Kriteria	Breadth First	Kedalaman Pertama	Dua arah	Biaya Seragam	Pendalaman Interaktif
Waktu	b ^d	b ^m	b ^{d / 2}	b ^d	b ^d
Ruang	b ^d	b ^m	b ^{d / 2}	b ^d	b ^d
Optimalitas	Iya	Tidak	Iya	Iya	Iya
Kelengkapan	Iya	Tidak	Iya	Iya	Iya

Strategi Pencarian Informasi (Heuristik)

Untuk memecahkan masalah besar dengan sejumlah besar kemungkinan status, pengetahuan khusus masalah perlu ditambahkan untuk meningkatkan efisiensi algoritme pencarian.

Fungsi Evaluasi Heuristik

Mereka menghitung biaya jalur optimal antara dua kondisi. Fungsi heuristik untuk permainan ubin geser dihitung dengan menghitung jumlah gerakan yang dilakukan setiap ubin dari status tujuannya dan menambahkan jumlah gerakan ini untuk semua ubin.

Pencarian Heuristik Murni

Ini memperluas node dalam urutan nilai heuristiknya. Ini membuat dua daftar, daftar tertutup untuk node yang sudah diperluas dan daftar terbuka untuk node yang dibuat tetapi tidak diperluas.

Di setiap iterasi, node dengan nilai heuristik minimum diperluas, semua node turunannya dibuat dan ditempatkan dalam daftar tertutup. Kemudian, fungsi heuristik diterapkan ke node turunan dan ditempatkan di daftar terbuka sesuai dengan nilai heuristiknya. Jalur yang lebih pendek disimpan dan yang lebih panjang dibuang.

Pencarian

Ini adalah bentuk pencarian Terbaik Pertama yang paling terkenal. Ini menghindari perluasan jalur yang sudah mahal, tetapi memperluas jalur yang paling menjanjikan terlebih dahulu.

f (n) = g (n) + h (n), di mana

g (n) biaya (sejauh ini) untuk mencapai node
h (n) perkiraan biaya untuk pergi dari node ke tujuan
f (n) perkiraan total biaya jalur melalui n ke tujuan. Ini diimplementasikan menggunakan antrian prioritas dengan meningkatkan f (n).

Pencarian Pertama Terbaik Serakah

Ini memperluas node yang diperkirakan paling dekat dengan tujuan. Ini memperluas node berdasarkan f (n) = h (n). Ini diimplementasikan menggunakan antrian prioritas.

Disadvantage- Ini bisa macet di loop. Itu tidak optimal.

Algoritma Pencarian Lokal

Mereka mulai dari solusi prospektif dan kemudian pindah ke solusi tetangga. Mereka dapat mengembalikan solusi yang valid meskipun itu terputus kapan saja sebelum berakhir.

Pencarian Mendaki Bukit

Ini adalah algoritme berulang yang dimulai dengan solusi sewenang-wenang untuk suatu masalah dan mencoba menemukan solusi yang lebih baik dengan mengubah satu elemen solusi secara bertahap. Jika perubahan menghasilkan solusi yang lebih baik, perubahan bertahap diambil sebagai solusi baru. Proses ini diulangi hingga tidak ada perbaikan lebih lanjut.

function Hill-Climbing (masalah), mengembalikan status maksimum lokal.

inputs: problem, a problem
local variables: current, a node
                 neighbor, a node
current <-Make_Node(Initial-State[problem])
loop
   do neighbor <- a highest_valued successor of current
      if Value[neighbor] ≤ Value[current] then
      return State[current]
      current <- neighbor				  
	
end

Disadvantage - Algoritma ini tidak lengkap, juga tidak optimal.

Pencarian Beam Lokal

Dalam algoritma ini, ia memegang k sejumlah negara pada waktu tertentu. Pada awalnya, status ini dibuat secara acak. Penerus status k ini dihitung dengan bantuan fungsi objektif. Jika salah satu penerus ini adalah nilai maksimum dari fungsi tujuan, algoritme berhenti.

Jika tidak, status (k awal awal dan jumlah k penerus status = 2k) status ditempatkan dalam sebuah kumpulan. Pool tersebut kemudian diurutkan secara numerik. Status k tertinggi dipilih sebagai status awal baru. Proses ini berlanjut hingga nilai maksimum tercapai.

function BeamSearch ( masalah, k ), mengembalikan status solusi.

start with k randomly generated states
loop
   generate all successors of all k states
   if any of the states = solution, then return the state
   else select the k best successors
end

Simulasi Annealing

Annealing adalah proses memanaskan dan mendinginkan logam untuk mengubah struktur internalnya untuk memodifikasi sifat fisiknya. Ketika logam mendingin, struktur barunya ditahan, dan logam tersebut mempertahankan sifat yang baru diperolehnya. Dalam proses simulasi anil, suhu dijaga tetap variabel.

Kami awalnya mengatur suhu tinggi dan kemudian membiarkannya 'mendingin' secara perlahan saat algoritme berlanjut. Ketika suhu tinggi, algoritme diizinkan untuk menerima solusi yang lebih buruk dengan frekuensi tinggi.

Mulailah

Inisialisasi k = 0; L = jumlah variabel integer;
Dari i → j, cari perbedaan performanya Δ.
Jika Δ <= 0 maka terima lagi jika exp (-Δ / T (k))> random (0,1) maka terima;
Ulangi langkah 1 dan 2 untuk langkah L (k).
k = k + 1;

Ulangi langkah 1 hingga 4 hingga kriteria terpenuhi.

Akhir

Masalah Penjual Bepergian

Dalam algoritme ini, tujuannya adalah untuk menemukan tur berbiaya rendah yang dimulai dari sebuah kota, mengunjungi semua kota dalam perjalanan tepat satu kali dan berakhir di kota awal yang sama.

Start
   Find out all (n -1)! Possible solutions, where n is the total number of cities.
   Determine the minimum cost by finding out the cost of each of these (n -1)! solutions.
   Finally, keep the one with the minimum cost.
end