Algoritma Paralel - Panduan Cepat

Sebuah algorithmmerupakan urutan langkah-langkah yang mengambil masukan dari pengguna dan setelah dilakukan beberapa komputasi menghasilkan keluaran. SEBUAHparallel algorithm adalah algoritma yang dapat menjalankan beberapa instruksi secara bersamaan pada perangkat pemrosesan yang berbeda dan kemudian menggabungkan semua keluaran individu untuk menghasilkan hasil akhir.

Pemrosesan Bersamaan

Ketersediaan komputer yang mudah seiring dengan pertumbuhan internet telah mengubah cara kita menyimpan dan memproses data. Kita hidup di zaman di mana data tersedia dengan berlimpah. Setiap hari kami berurusan dengan volume data yang sangat besar yang membutuhkan komputasi kompleks dan itu juga, dalam waktu cepat. Terkadang, kita perlu mengambil data dari peristiwa serupa atau saling terkait yang terjadi secara bersamaan. Di sinilah kita membutuhkanconcurrent processing yang dapat membagi tugas yang kompleks dan memprosesnya beberapa sistem untuk menghasilkan keluaran dalam waktu cepat.

Pemrosesan bersamaan sangat penting di mana tugas melibatkan pemrosesan sejumlah besar data kompleks. Contohnya termasuk - mengakses database besar, pengujian pesawat terbang, perhitungan astronomi, fisika atom dan nuklir, analisis biomedis, perencanaan ekonomi, pemrosesan gambar, robotika, prakiraan cuaca, layanan berbasis web, dll.

Apa itu Paralelisme?

Parallelismadalah proses memproses beberapa set instruksi secara bersamaan. Ini mengurangi total waktu komputasi. Paralelisme dapat diimplementasikan dengan menggunakanparallel computers,yaitu komputer dengan banyak prosesor. Komputer paralel membutuhkan algoritma paralel, bahasa pemrograman, kompiler dan sistem operasi yang mendukung multitasking.

Dalam tutorial ini, kita hanya akan membahas tentang parallel algorithms. Sebelum melangkah lebih jauh, mari kita bahas dulu tentang algoritma dan tipenya.

Apa itu Algoritma?

Sebuah algorithmadalah urutan instruksi yang diikuti untuk memecahkan masalah. Saat merancang suatu algoritma, kita harus mempertimbangkan arsitektur komputer tempat algoritma tersebut akan dieksekusi. Sesuai arsitekturnya, ada dua jenis komputer -

Komputer Berurutan
Komputer Paralel

Bergantung pada arsitektur komputer, kami memiliki dua jenis algoritme -

Sequential Algorithm - Algoritme di mana beberapa langkah instruksi yang berurutan dijalankan dalam urutan kronologis untuk menyelesaikan masalah.
Parallel Algorithm- Masalah dibagi menjadi sub-masalah dan dijalankan secara paralel untuk mendapatkan keluaran individu. Nanti, keluaran individu ini digabungkan bersama untuk mendapatkan keluaran akhir yang diinginkan.

Tidaklah mudah untuk membagi masalah besar menjadi sub-problems. Sub-masalah mungkin memiliki ketergantungan data di antara mereka. Oleh karena itu, para prosesor harus saling berkomunikasi untuk menyelesaikan masalah tersebut.

Ditemukan bahwa waktu yang dibutuhkan oleh prosesor dalam berkomunikasi satu sama lain lebih banyak daripada waktu pemrosesan yang sebenarnya. Jadi, saat mendesain algoritme paralel, penggunaan CPU yang tepat harus dipertimbangkan untuk mendapatkan algoritme yang efisien.

Untuk mendesain algoritma dengan benar, kita harus memiliki ide dasar yang jelas model of computation di komputer paralel.

Model Komputasi

Baik komputer sekuensial dan paralel beroperasi pada sekumpulan (aliran) instruksi yang disebut algoritma. Serangkaian instruksi (algoritme) ini menginstruksikan komputer tentang apa yang harus dilakukannya di setiap langkah.

Bergantung pada aliran instruksi dan aliran data, komputer dapat diklasifikasikan menjadi empat kategori -

Aliran instruksi tunggal, aliran data tunggal (SISD) komputer
Aliran instruksi tunggal, aliran data banyak (SIMD) komputer
Beberapa aliran Instruksi, aliran Data Tunggal (MISD) komputer
Multiple Instruction stream, Multiple Data stream (MIMD) komputer

Komputer SISD

Komputer SISD berisi one control unit, one processing unit, dan one memory unit.

Dalam jenis komputer ini, prosesor menerima aliran instruksi tunggal dari unit kontrol dan beroperasi pada aliran data tunggal dari unit memori. Selama komputasi, pada setiap langkah, prosesor menerima satu instruksi dari unit kontrol dan beroperasi pada satu data yang diterima dari unit memori.

Komputer SIMD

Komputer SIMD berisi one control unit, multiple processing units, dan shared memory or interconnection network.

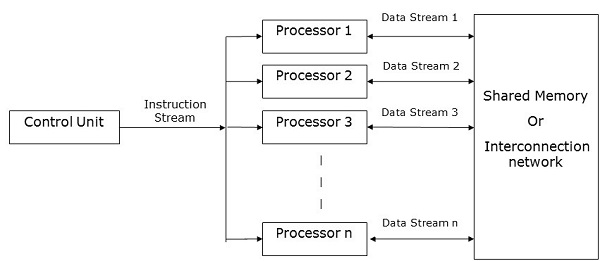
Di sini, satu unit kontrol tunggal mengirimkan instruksi ke semua unit pemrosesan. Selama komputasi, pada setiap langkah, semua prosesor menerima satu set instruksi dari unit kontrol dan beroperasi pada kumpulan data yang berbeda dari unit memori.

Setiap unit pemrosesan memiliki unit memori lokalnya sendiri untuk menyimpan data dan instruksi. Di komputer SIMD, prosesor perlu berkomunikasi di antara mereka sendiri. Ini dilakukan olehshared memory atau oleh interconnection network.

Sementara beberapa prosesor menjalankan serangkaian instruksi, prosesor yang tersisa menunggu rangkaian instruksi berikutnya. Instruksi dari unit kontrol memutuskan prosesor mana yang akan digunakanactive (jalankan instruksi) atau inactive (tunggu instruksi selanjutnya).

Komputer MISD

Seperti namanya, komputer MISD mengandung multiple control units, multiple processing units, dan one common memory unit.

Di sini, setiap prosesor memiliki unit kontrolnya sendiri dan mereka berbagi unit memori yang sama. Semua prosesor mendapatkan instruksi secara individual dari unit kontrol mereka sendiri dan mereka beroperasi pada aliran data tunggal sesuai instruksi yang mereka terima dari unit kontrol masing-masing. Prosesor ini beroperasi secara bersamaan.

Komputer MIMD

Komputer MIMD memiliki multiple control units, multiple processing units, dan a shared memory atau interconnection network.

Di sini, setiap prosesor memiliki unit kontrolnya sendiri, unit memori lokal, dan unit aritmatika dan logika. Mereka menerima set instruksi yang berbeda dari unit kontrol masing-masing dan beroperasi pada set data yang berbeda.

Catatan

Komputer MIMD yang berbagi memori yang sama dikenal sebagai multiprocessors, sedangkan yang menggunakan jaringan interkoneksi disebut multicomputers.
Berdasarkan jarak fisik prosesor, multikomputer terdiri dari dua jenis -
- Multicomputer - Ketika semua prosesor sangat dekat satu sama lain (misalnya, di ruangan yang sama).
- Distributed system - Ketika semua prosesor berada jauh dari satu sama lain (misalnya - di kota yang berbeda)

Analisis suatu algoritma membantu kita menentukan apakah algoritma tersebut berguna atau tidak. Umumnya, algoritme dianalisis berdasarkan waktu eksekusinya(Time Complexity) dan jumlah ruang (Space Complexity) itu membutuhkan.

Karena kami memiliki perangkat memori canggih yang tersedia dengan biaya yang wajar, ruang penyimpanan tidak lagi menjadi masalah. Karenanya, kompleksitas ruang tidak terlalu dianggap penting.

Algoritma paralel dirancang untuk meningkatkan kecepatan komputasi komputer. Untuk menganalisis Algoritma Paralel, kami biasanya mempertimbangkan parameter berikut -

Kompleksitas waktu (Execution Time),
Jumlah total prosesor yang digunakan, dan
Total biaya.

Kompleksitas Waktu

Alasan utama di balik pengembangan algoritma paralel adalah untuk mengurangi waktu komputasi suatu algoritma. Dengan demikian, mengevaluasi waktu eksekusi suatu algoritma sangat penting dalam menganalisis efisiensinya.

Waktu eksekusi diukur berdasarkan waktu yang dibutuhkan oleh algoritma untuk memecahkan masalah. Total waktu eksekusi dihitung dari saat algoritme mulai mengeksekusi hingga saat berhenti. Jika semua prosesor tidak memulai atau mengakhiri eksekusi pada saat bersamaan, maka total waktu eksekusi dari algoritme adalah saat prosesor pertama memulai eksekusinya hingga saat prosesor terakhir menghentikan eksekusinya.

Kompleksitas waktu dari suatu algoritma dapat diklasifikasikan menjadi tiga kategori-

Worst-case complexity - Ketika jumlah waktu yang dibutuhkan oleh algoritma untuk input yang diberikan adalah maximum.
Average-case complexity - Ketika jumlah waktu yang dibutuhkan oleh algoritma untuk input yang diberikan adalah average.
Best-case complexity - Ketika jumlah waktu yang dibutuhkan oleh algoritma untuk input yang diberikan adalah minimum.

Analisis Asymptotic

Kompleksitas atau efisiensi suatu algoritma adalah banyaknya langkah yang dijalankan oleh algoritma tersebut untuk mendapatkan keluaran yang diinginkan. Analisis asimtotik dilakukan untuk menghitung kompleksitas suatu algoritma dalam analisis teoritisnya. Dalam analisis asimtotik, panjang input yang besar digunakan untuk menghitung fungsi kompleksitas algoritme.

Note - Asymptoticadalah kondisi dimana garis cenderung bertemu dengan kurva, tetapi tidak berpotongan. Di sini garis dan kurva tidak menunjukkan gejala satu sama lain.

Notasi asimtotik adalah cara termudah untuk mendeskripsikan waktu eksekusi tercepat dan paling lambat untuk algoritme yang menggunakan batas tinggi dan batas rendah pada kecepatan. Untuk ini, kami menggunakan notasi berikut -

Notasi Big O
Notasi omega
Notasi theta

Notasi Big O

Dalam matematika, notasi Big O digunakan untuk merepresentasikan karakteristik asimtotik fungsi. Ini mewakili perilaku suatu fungsi untuk input besar dalam metode yang sederhana dan akurat. Ini adalah metode untuk mewakili batas atas waktu eksekusi algoritme. Ini mewakili jumlah waktu terlama yang diperlukan algoritme untuk menyelesaikan eksekusinya. Fungsi -

f (n) = O (g (n))

jika ada konstanta positif c dan n₀ seperti yang f(n) ≤ c * g(n) untuk semua n dimana n ≥ n₀.

Notasi omega

Notasi omega adalah metode untuk merepresentasikan batas bawah waktu eksekusi suatu algoritma. Fungsi -

f (n) = Ω (g (n))

jika ada konstanta positif c dan n₀ seperti yang f(n) ≥ c * g(n) untuk semua n dimana n ≥ n₀.

Notasi Theta

Notasi teta adalah metode yang merepresentasikan batas bawah dan batas atas dari waktu eksekusi suatu algoritma. Fungsi -

f (n) = θ (g (n))

jika ada konstanta positif c₁, c₂, dan n₀ sedemikian rupa sehingga c1 * g (n) ≤ f (n) ≤ c2 * g (n) untuk semua n dimana n ≥ n₀.

Mempercepat Algoritma

Kinerja dari algoritma paralel ditentukan dengan menghitungnya speedup. Speedup didefinisikan sebagai rasio waktu eksekusi kasus terburuk dari algoritma sekuensial tercepat yang diketahui untuk masalah tertentu dengan waktu eksekusi kasus terburuk dari algoritma paralel.

speedup =

Waktu eksekusi kasus terburuk dari sekuensial tercepat yang diketahui untuk masalah tertentu / Waktu eksekusi kasus terburuk dari algoritme paralel

Jumlah Prosesor yang Digunakan

Jumlah prosesor yang digunakan merupakan faktor penting dalam menganalisis efisiensi algoritma paralel. Biaya untuk membeli, memelihara, dan menjalankan komputer dihitung. Semakin besar jumlah prosesor yang digunakan oleh algoritme untuk menyelesaikan masalah, semakin mahal hasil yang diperoleh.

Total biaya

Biaya total dari algoritme paralel adalah produk dari kompleksitas waktu dan jumlah prosesor yang digunakan dalam algoritme tersebut.

Total Biaya = Kompleksitas waktu × Jumlah prosesor yang digunakan

Oleh karena itu, efficiency dari algoritma paralel adalah -

Efisiensi =

Waktu eksekusi kasus terburuk dari algoritma sekuensial / Waktu eksekusi kasus terburuk dari algoritma paralel

Model algoritma paralel dikembangkan dengan mempertimbangkan strategi pembagian data dan metode pengolahan serta menerapkan strategi yang sesuai untuk mengurangi interaksi. Pada bab ini, kita akan membahas Model Algoritma Paralel berikut -

Model paralel data
Model grafik tugas
Model kolam kerja
Model budak master
Konsumen produsen atau model saluran pipa
Model hibrida

Data Paralel

Dalam model paralel data, tugas diberikan ke proses dan setiap tugas melakukan jenis operasi serupa pada data yang berbeda. Data parallelism merupakan konsekuensi dari operasi tunggal yang diterapkan pada beberapa item data.

Model data-paralel dapat diterapkan pada ruang alamat bersama dan paradigma penyampaian pesan. Dalam model data-paralel, overhead interaksi dapat dikurangi dengan memilih lokalitas yang mempertahankan dekomposisi, dengan menggunakan rutinitas interaksi kolektif yang dioptimalkan, atau dengan komputasi dan interaksi yang tumpang tindih.

Karakteristik utama dari masalah model data-paralel adalah bahwa intensitas paralelisme data meningkat dengan ukuran masalah, yang pada gilirannya memungkinkan untuk menggunakan lebih banyak proses untuk memecahkan masalah yang lebih besar.

Example - Perkalian matriks padat.

Model Grafik Tugas

Dalam model grafik tugas, paralelisme dinyatakan dengan a task graph. Grafik tugas dapat berupa trivial atau nontrivial. Dalam model ini, korelasi antara tugas digunakan untuk mempromosikan lokalitas atau meminimalkan biaya interaksi. Model ini diterapkan untuk memecahkan masalah di mana kuantitas data yang terkait dengan tugas-tugas sangat besar dibandingkan dengan jumlah komputasi yang terkait dengannya. Tugas diberikan untuk membantu meningkatkan biaya perpindahan data di antara tugas-tugas tersebut.

Examples - Pengurutan cepat paralel, faktorisasi matriks renggang, dan algoritme paralel yang diturunkan melalui pendekatan divide-and-conquer.

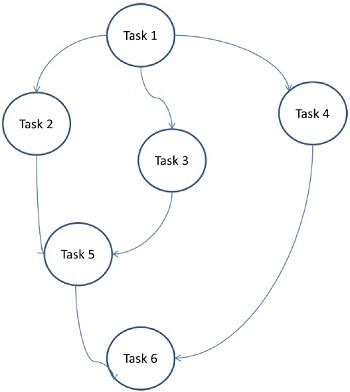
Di sini, masalah dibagi menjadi tugas atom dan diimplementasikan sebagai grafik. Setiap tugas adalah unit pekerjaan independen yang memiliki ketergantungan pada satu atau lebih tugas sebelumnya. Setelah menyelesaikan tugas, output dari tugas sebelumnya diteruskan ke tugas dependen. Sebuah tugas dengan tugas anteseden memulai eksekusi hanya ketika seluruh tugas antesedennya selesai. Hasil akhir grafik diterima saat tugas dependen terakhir diselesaikan (Tugas 6 pada gambar di atas).

Model Kolam Kerja

Dalam model kumpulan kerja, tugas ditetapkan secara dinamis ke proses untuk menyeimbangkan beban. Oleh karena itu, proses apa pun berpotensi menjalankan tugas apa pun. Model ini digunakan ketika jumlah data yang terkait dengan tugas relatif lebih kecil daripada komputasi yang terkait dengan tugas.

Tidak ada penetapan tugas yang diinginkan ke dalam proses. Penetapan tugas terpusat atau terdesentralisasi. Pointer ke tugas disimpan dalam daftar yang dibagikan secara fisik, dalam antrian prioritas, atau dalam tabel atau pohon hash, atau mereka dapat disimpan dalam struktur data yang didistribusikan secara fisik.

Tugas mungkin tersedia di awal, atau dapat dibuat secara dinamis. Jika tugas dibuat secara dinamis dan penetapan tugas yang terdesentralisasi dilakukan, maka algoritme pendeteksian penghentian diperlukan sehingga semua proses benar-benar dapat mendeteksi penyelesaian keseluruhan program dan berhenti mencari tugas lainnya.

Example - Pencarian pohon paralel

Model Master-Budak

Dalam model master-slave, satu atau lebih proses master menghasilkan tugas dan mengalokasikannya ke proses slave. Tugas dapat dialokasikan sebelumnya jika -

master dapat memperkirakan volume tugas, atau
penugasan acak dapat melakukan pekerjaan yang memuaskan untuk menyeimbangkan beban, atau
budak diberi tugas yang lebih kecil pada waktu yang berbeda.

Model ini umumnya sama-sama cocok untuk shared-address-space atau message-passing paradigms, karena interaksi secara alami ada dua cara.

Dalam beberapa kasus, tugas mungkin perlu diselesaikan secara bertahap, dan tugas di setiap tahap harus diselesaikan sebelum tugas di tahap berikutnya dapat dibuat. Model master-slave dapat digeneralisasikan menjadihierarchical atau multi-level master-slave model di mana master tingkat atas memberikan sebagian besar tugas ke master tingkat kedua, yang selanjutnya membagi tugas di antara budaknya sendiri dan dapat melakukan sebagian dari tugas itu sendiri.

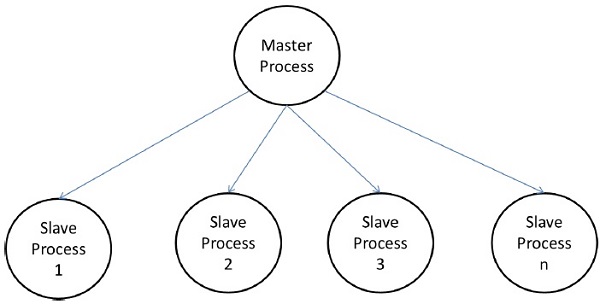
Tindakan pencegahan dalam menggunakan model master-slave

Perhatian harus diberikan untuk memastikan bahwa master tidak menjadi titik kemacetan. Ini mungkin terjadi jika tugas-tugasnya terlalu kecil atau para pekerja relatif cepat.

Tugas-tugas harus dipilih sedemikian rupa sehingga biaya pelaksanaan tugas mendominasi biaya komunikasi dan biaya sinkronisasi.

Interaksi asynchronous dapat membantu interaksi tumpang tindih dan perhitungan yang terkait dengan pembuatan pekerjaan oleh master.

Model Pipa

Itu juga dikenal sebagai producer-consumer model. Di sini sekumpulan data diteruskan melalui serangkaian proses, yang masing-masing melakukan beberapa tugas padanya. Di sini, kedatangan data baru menghasilkan eksekusi tugas baru dengan proses dalam antrian. Proses tersebut dapat membentuk antrian dalam bentuk array linier atau multidimensi, pohon, atau grafik umum dengan atau tanpa siklus.

Model ini merupakan rantai produsen dan konsumen. Setiap proses dalam antrian dapat dianggap sebagai konsumen dari urutan item data untuk proses sebelumnya dalam antrian dan sebagai penghasil data untuk proses yang mengikutinya dalam antrian. Antrian tidak harus berupa rantai linier; itu bisa menjadi grafik berarah. Teknik minimisasi interaksi yang paling umum berlaku untuk model ini adalah interaksi yang tumpang tindih dengan komputasi.

Example - Algoritma faktorisasi LU paralel.

Model Hibrida

Model algoritme hibrid diperlukan jika lebih dari satu model mungkin diperlukan untuk memecahkan masalah.

Model hybrid dapat terdiri dari beberapa model yang diterapkan secara hierarki atau beberapa model yang diterapkan secara berurutan ke fase berbeda dari algoritme paralel.

Example - Urutan cepat paralel

Parallel Random Access Machines (PRAM)adalah model, yang dianggap untuk sebagian besar algoritme paralel. Di sini, beberapa prosesor dipasang ke satu blok memori. Model PRAM berisi -

Seperangkat prosesor sejenis.
Semua prosesor berbagi unit memori yang sama. Prosesor dapat berkomunikasi di antara mereka sendiri hanya melalui memori bersama.
Unit akses memori (MAU) menghubungkan prosesor dengan satu memori bersama.

Sini, n jumlah prosesor dapat melakukan operasi independen njumlah data dalam satuan waktu tertentu. Ini dapat mengakibatkan akses simultan dari lokasi memori yang sama oleh prosesor yang berbeda.

Untuk mengatasi masalah ini, kendala berikut telah diterapkan pada model PRAM -

Exclusive Read Exclusive Write (EREW) - Di sini tidak ada dua prosesor yang diizinkan untuk membaca atau menulis ke lokasi memori yang sama pada waktu yang sama.
Exclusive Read Concurrent Write (ERCW) - Di sini tidak ada dua prosesor yang diizinkan untuk membaca dari lokasi memori yang sama pada waktu yang sama, tetapi diizinkan untuk menulis ke lokasi memori yang sama pada waktu yang sama.
Concurrent Read Exclusive Write (CREW) - Di sini semua prosesor diizinkan untuk membaca dari lokasi memori yang sama pada waktu yang sama, tetapi tidak diizinkan untuk menulis ke lokasi memori yang sama pada waktu yang sama.
Concurrent Read Concurrent Write (CRCW) - Semua prosesor diizinkan untuk membaca atau menulis ke lokasi memori yang sama pada waktu yang sama.

Ada banyak metode untuk mengimplementasikan model PRAM, tetapi yang paling menonjol adalah -

Model memori bersama
Model penyampaian pesan
Model paralel data

Model Memori Bersama

Memori bersama menekankan pada control parallelism dari pada data parallelism. Dalam model memori bersama, beberapa proses dijalankan pada prosesor yang berbeda secara independen, tetapi mereka berbagi ruang memori yang sama. Karena aktivitas prosesor apa pun, jika ada perubahan di lokasi memori mana pun, itu terlihat oleh seluruh prosesor.

Karena beberapa prosesor mengakses lokasi memori yang sama, mungkin saja terjadi pada titik waktu tertentu, lebih dari satu prosesor mengakses lokasi memori yang sama. Misalkan yang satu membaca lokasi itu dan yang lainnya sedang menulis di lokasi itu. Ini dapat menimbulkan kebingungan. Untuk menghindarinya, beberapa mekanisme kontrol, sepertilock / semaphore, diterapkan untuk memastikan saling pengecualian.

Pemrograman memori bersama telah diimplementasikan sebagai berikut -

Thread libraries- Pustaka utas memungkinkan beberapa utas kontrol yang berjalan secara bersamaan di lokasi memori yang sama. Pustaka benang menyediakan antarmuka yang mendukung multithreading melalui pustaka subrutin. Ini berisi subrutin untuk
- Membuat dan menghancurkan utas
- Menjadwalkan eksekusi utas
- melewatkan data dan pesan antar utas
- menyimpan dan memulihkan konteks utas

Contoh pustaka utas termasuk - utas SolarisTM untuk Solaris, utas POSIX seperti yang diterapkan di Linux, utas Win32 tersedia di Windows NT dan Windows 2000, dan utas JavaTM sebagai bagian dari JavaTM Development Kit (JDK) standar.

Distributed Shared Memory (DSM) Systems- Sistem DSM membuat abstraksi memori bersama pada arsitektur yang digabungkan secara longgar untuk mengimplementasikan pemrograman memori bersama tanpa dukungan perangkat keras. Mereka menerapkan pustaka standar dan menggunakan fitur manajemen memori tingkat pengguna tingkat lanjut yang ada dalam sistem operasi modern. Contohnya termasuk Tread Marks System, Munin, IVY, Shasta, Brazos, dan Cashmere.
Program Annotation Packages- Ini diimplementasikan pada arsitektur yang memiliki karakteristik akses memori yang seragam. Contoh paling terkenal dari paket anotasi program adalah OpenMP. OpenMP mengimplementasikan paralelisme fungsional. Ini terutama berfokus pada paralelisasi loop.

Konsep memori bersama menyediakan kontrol tingkat rendah dari sistem memori bersama, tetapi cenderung membosankan dan keliru. Ini lebih dapat diterapkan untuk pemrograman sistem daripada pemrograman aplikasi.

Manfaat Pemrograman Memori Bersama

Ruang alamat global memberikan pendekatan pemrograman yang mudah digunakan untuk memori.
Karena kedekatan memori dengan CPU, berbagi data antar proses menjadi cepat dan seragam.
Tidak perlu secara khusus menjelaskan komunikasi data antar proses.
Overhead proses-komunikasi dapat diabaikan.
Sangat mudah dipelajari.

Kekurangan Pemrograman Memori Bersama

Ini tidak portabel.
Mengelola lokalitas data sangat sulit.

Model Penyampaian Pesan

Pengiriman pesan adalah pendekatan pemrograman paralel yang paling umum digunakan dalam sistem memori terdistribusi. Di sini, programmer harus menentukan paralelisme. Dalam model ini, semua prosesor memiliki unit memori lokalnya sendiri dan mereka bertukar data melalui jaringan komunikasi.

Prosesor menggunakan pustaka penyampaian pesan untuk komunikasi di antara mereka sendiri. Bersama dengan data yang dikirim, pesan tersebut berisi komponen berikut -

Alamat prosesor yang mengirim pesan;
Alamat awal dari lokasi memori data di prosesor pengirim;
Jenis data dari data pengiriman;
Ukuran data dari pengiriman data;
Alamat prosesor yang menjadi tujuan pengiriman pesan;
Alamat awal dari lokasi memori untuk data di prosesor penerima.

Prosesor dapat berkomunikasi satu sama lain dengan salah satu metode berikut -

Komunikasi Point-to-Point
Komunikasi Kolektif
Antarmuka Penerusan Pesan

Komunikasi Point-to-Point

Komunikasi titik-ke-titik adalah bentuk penyampaian pesan yang paling sederhana. Di sini, pesan dapat dikirim dari prosesor pengirim ke prosesor penerima dengan salah satu mode transfer berikut -

Synchronous mode - Pesan berikutnya dikirim hanya setelah menerima konfirmasi bahwa pesan sebelumnya telah terkirim, untuk mempertahankan urutan pesan.
Asynchronous mode - Untuk mengirim pesan berikutnya, tidak diperlukan penerimaan konfirmasi pengiriman pesan sebelumnya.

Komunikasi Kolektif

Komunikasi kolektif melibatkan lebih dari dua prosesor untuk penyampaian pesan. Mode berikut memungkinkan komunikasi kolektif -

Barrier - Mode penghalang dimungkinkan jika semua prosesor yang termasuk dalam komunikasi menjalankan bock tertentu (dikenal sebagai barrier block) untuk penyampaian pesan.
Broadcast - Penyiaran terdiri dari dua jenis -
- One-to-all - Di sini, satu prosesor dengan satu operasi mengirimkan pesan yang sama ke semua prosesor lainnya.
- All-to-all - Di sini, semua prosesor mengirim pesan ke semua prosesor lainnya.

Pesan yang disiarkan mungkin terdiri dari tiga jenis -

Personalized - Pesan unik dikirim ke semua prosesor tujuan lainnya.
Non-personalized - Semua prosesor tujuan menerima pesan yang sama.
Reduction - Dalam penyiaran reduksi, satu prosesor dalam grup mengumpulkan semua pesan dari semua prosesor lain dalam grup dan menggabungkannya ke satu pesan yang dapat diakses oleh semua prosesor lain dalam grup.

Manfaat Pengiriman Pesan

Memberikan kontrol paralelisme tingkat rendah;
Ini portabel;
Lebih sedikit rawan kesalahan;
Lebih sedikit overhead dalam sinkronisasi paralel dan distribusi data.

Kekurangan Penyampaian Pesan

Dibandingkan dengan kode memori bersama paralel, kode penyampaian pesan umumnya membutuhkan lebih banyak biaya perangkat lunak.

Perpustakaan yang Melewati Pesan

Ada banyak perpustakaan penyampaian pesan. Di sini, kita akan membahas dua pustaka penyampaian pesan yang paling banyak digunakan -

Message Passing Interface (MPI)
Mesin Virtual Paralel (PVM)

Message Passing Interface (MPI)

Ini adalah standar universal untuk menyediakan komunikasi di antara semua proses bersamaan dalam sistem memori terdistribusi. Sebagian besar platform komputasi paralel yang umum digunakan menyediakan setidaknya satu implementasi antarmuka penyampaian pesan. Ini telah diimplementasikan sebagai kumpulan fungsi yang telah ditentukan sebelumnya yang disebutlibrary dan dapat dipanggil dari bahasa seperti C, C ++, Fortran, dll. MPI cepat dan portabel dibandingkan dengan pustaka penyampaian pesan lainnya.

Merits of Message Passing Interface

Berjalan hanya pada arsitektur memori bersama atau arsitektur memori terdistribusi;
Setiap prosesor memiliki variabel lokalnya sendiri;
Dibandingkan dengan komputer memori bersama yang besar, komputer memori terdistribusi lebih murah.

Demerits of Message Passing Interface

Lebih banyak perubahan pemrograman diperlukan untuk algoritma paralel;
Terkadang sulit untuk di-debug; dan
Tidak bekerja dengan baik dalam jaringan komunikasi antar node.

Mesin Virtual Paralel (PVM)

PVM adalah sistem penyampaian pesan portabel, yang dirancang untuk menghubungkan mesin host heterogen yang terpisah untuk membentuk satu mesin virtual. Ini adalah sumber daya komputasi paralel tunggal yang dapat dikelola. Masalah komputasi yang besar seperti studi superkonduktivitas, simulasi dinamika molekul, dan algoritme matriks dapat diselesaikan dengan biaya yang lebih efektif dengan menggunakan memori dan daya agregat dari banyak komputer. Ia mengatur semua perutean pesan, konversi data, penjadwalan tugas di jaringan arsitektur komputer yang tidak kompatibel.

Features of PVM

Sangat mudah dipasang dan dikonfigurasi;
Banyak pengguna dapat menggunakan PVM secara bersamaan;
Satu pengguna dapat menjalankan banyak aplikasi;
Ini paket kecil;
Mendukung C, C ++, Fortran;
Untuk menjalankan program PVM tertentu, pengguna dapat memilih grup mesin;
Ini adalah model penyampaian pesan,
Perhitungan berbasis proses;
Mendukung arsitektur heterogen.

Pemrograman Data Paralel

Fokus utama dari model pemrograman data paralel adalah melakukan operasi pada kumpulan data secara bersamaan. Kumpulan data diatur ke dalam beberapa struktur seperti array, hypercube, dll. Prosesor melakukan operasi secara kolektif pada struktur data yang sama. Setiap tugas dilakukan pada partisi berbeda dari struktur data yang sama.

Ini membatasi, karena tidak semua algoritme dapat ditentukan dalam hal paralelisme data. Inilah alasan mengapa paralelisme data tidak universal.

Bahasa paralel data membantu menentukan dekomposisi data dan pemetaan ke prosesor. Ini juga termasuk pernyataan distribusi data yang memungkinkan pemrogram untuk memiliki kendali atas data - misalnya, data mana yang akan pergi ke prosesor mana - untuk mengurangi jumlah komunikasi di dalam prosesor.

Untuk menerapkan algoritme apa pun dengan benar, Anda harus memilih struktur data yang tepat. Ini karena operasi tertentu yang dilakukan pada struktur data mungkin memerlukan lebih banyak waktu dibandingkan dengan operasi yang sama yang dilakukan pada struktur data lain.

Example- Untuk mengakses elemen ^ke- i dalam suatu himpunan dengan menggunakan larik, mungkin diperlukan waktu yang konstan tetapi dengan menggunakan daftar tertaut, waktu yang diperlukan untuk melakukan operasi yang sama dapat menjadi polinomial.

Oleh karena itu, pemilihan struktur data harus dilakukan dengan mempertimbangkan arsitektur dan jenis operasi yang akan dilakukan.

Struktur data berikut biasanya digunakan dalam pemrograman paralel -

Daftar Tertaut
Arrays
Jaringan Hypercube

Daftar Tertaut

Daftar tertaut adalah struktur data yang memiliki nol atau lebih node yang dihubungkan oleh pointer. Node mungkin atau mungkin tidak menempati lokasi memori yang berurutan. Setiap node memiliki dua atau tiga bagian - satudata part yang menyimpan data dan dua lainnya link fieldsyang menyimpan alamat node sebelumnya atau berikutnya. Alamat node pertama disimpan di pointer eksternal yang disebuthead. Node terakhir, yang dikenal sebagaitail, umumnya tidak mengandung alamat apapun.

Ada tiga jenis daftar tertaut -

Daftar Tertaut Tunggal
Daftar Tertaut Ganda
Daftar Tertaut Melingkar

Daftar Tertaut Tunggal

Sebuah node dari daftar tertaut tunggal berisi data dan alamat dari node berikutnya. Penunjuk eksternal disebuthead menyimpan alamat node pertama.

Daftar Tertaut Ganda

Node dari daftar tertaut ganda berisi data dan alamat dari node sebelumnya dan berikutnya. Penunjuk eksternal disebuthead menyimpan alamat dari node pertama dan pointer eksternal dipanggil tail menyimpan alamat node terakhir.

Daftar Tertaut Melingkar

Daftar tertaut melingkar sangat mirip dengan daftar tertaut tunggal kecuali fakta bahwa simpul terakhir menyimpan alamat simpul pertama.

Array

Array adalah struktur data tempat kita dapat menyimpan jenis data yang serupa. Ini bisa satu dimensi atau multi-dimensi. Array dapat dibuat secara statis atau dinamis.

Di statically declared arrays, dimensi dan ukuran array diketahui pada saat kompilasi.
Di dynamically declared arrays, dimensi dan ukuran larik diketahui saat runtime.

Untuk pemrograman memori bersama, array dapat digunakan sebagai memori umum dan untuk pemrograman paralel data, array dapat digunakan dengan mempartisi ke dalam sub-array.

Jaringan Hypercube

Arsitektur Hypercube sangat membantu untuk algoritma paralel tersebut di mana setiap tugas harus berkomunikasi dengan tugas lain. Topologi hypercube dapat dengan mudah menanamkan topologi lain seperti ring dan mesh. Ia juga dikenal sebagai n-kubus, di mananadalah jumlah dimensi. Hypercube dapat dibangun secara rekursif.

Memilih teknik perancangan yang tepat untuk algoritma paralel adalah tugas yang paling sulit dan penting. Sebagian besar masalah pemrograman paralel mungkin memiliki lebih dari satu solusi. Pada bab ini, kita akan membahas teknik perancangan berikut untuk algoritma paralel -

Memecah dan menaklukkan
Metode Serakah
Pemrograman Dinamis
Backtracking
Branch & Bound
Pemrograman Linear

Metode Pisahkan dan Taklukkan

Dalam pendekatan divide and conquer, masalah dibagi menjadi beberapa sub-masalah kecil. Kemudian sub masalah diselesaikan secara rekursif dan digabungkan untuk mendapatkan solusi dari masalah aslinya.

Pendekatan divide and conquer melibatkan langkah-langkah berikut di setiap level -

Divide - Masalah asli dibagi menjadi sub-sub masalah.
Conquer - Sub-masalah diselesaikan secara rekursif.
Combine - Solusi dari sub-masalah digabungkan untuk mendapatkan solusi dari masalah aslinya.

Pendekatan divide and conquer diterapkan dalam algoritma berikut -

Pencarian biner
Urutan cepat
Gabungkan urutan
Perkalian bilangan bulat
Inversi matriks
Perkalian matriks

Metode Serakah

Dalam algoritma serakah untuk mengoptimalkan solusi, solusi terbaik dipilih setiap saat. Algoritma rakus sangat mudah diterapkan pada masalah yang kompleks. Ini memutuskan langkah mana yang akan memberikan solusi paling akurat di langkah berikutnya.

Algoritma ini disebut greedykarena ketika solusi optimal untuk instance yang lebih kecil disediakan, algoritme tidak mempertimbangkan program total secara keseluruhan. Setelah solusi dipertimbangkan, algoritme rakus tidak akan pernah mempertimbangkan solusi yang sama lagi.

Algoritme rakus bekerja secara rekursif membuat sekelompok objek dari bagian komponen sekecil mungkin. Rekursi adalah prosedur untuk memecahkan masalah di mana solusi untuk masalah tertentu bergantung pada solusi dari contoh masalah yang lebih kecil.

Pemrograman Dinamis

Pemrograman dinamis adalah teknik pengoptimalan, yang membagi masalah menjadi sub-sub masalah yang lebih kecil dan setelah menyelesaikan setiap sub-masalah, pemrograman dinamis menggabungkan semua solusi untuk mendapatkan solusi akhir. Tidak seperti metode divide and conquer, pemrograman dinamis menggunakan kembali solusi untuk sub-masalah berkali-kali.

Algoritma rekursif untuk Fibonacci Series adalah contoh pemrograman dinamis.

Algoritma Mundur

Backtracking adalah teknik optimasi untuk menyelesaikan masalah kombinasional. Ini diterapkan pada masalah programatik dan kehidupan nyata. Masalah delapan ratu, teka-teki Sudoku dan melewati labirin adalah contoh populer di mana algoritma mundur digunakan.

Dalam penelusuran mundur, kami mulai dengan solusi yang memungkinkan, yang memenuhi semua kondisi yang diperlukan. Kemudian kami pindah ke tingkat berikutnya dan jika tingkat tersebut tidak menghasilkan solusi yang memuaskan, kami kembali satu tingkat ke belakang dan mulai dengan opsi baru.

Branch and Bound

Algoritma branch and bound merupakan teknik optimasi untuk mendapatkan solusi yang optimal dari masalah tersebut. Ini mencari solusi terbaik untuk masalah tertentu di seluruh ruang solusi. Batasan dalam fungsi yang akan dioptimalkan digabungkan dengan nilai solusi terbaik terbaru. Ini memungkinkan algoritme untuk menemukan bagian ruang solusi sepenuhnya.

Tujuan dari pencarian cabang dan terikat adalah untuk mempertahankan jalur biaya terendah ke sebuah target. Setelah solusi ditemukan, solusi tersebut dapat terus ditingkatkan. Pencarian bercabang dan terikat diimplementasikan dalam pencarian yang dibatasi kedalaman dan pencarian kedalaman-pertama.

Pemrograman Linear

Pemrograman linier menggambarkan kelas pekerjaan pengoptimalan yang luas di mana kriteria pengoptimalan dan batasannya adalah fungsi linier. Ini adalah teknik untuk mendapatkan hasil terbaik seperti keuntungan maksimum, jalur terpendek, atau biaya terendah.

Dalam pemrograman ini, kita memiliki seperangkat variabel dan kita harus menetapkan nilai absolut padanya untuk memenuhi seperangkat persamaan linier dan untuk memaksimalkan atau meminimalkan fungsi tujuan linier yang diberikan.

Matriks adalah sekumpulan data numerik dan non-numerik yang disusun dalam jumlah baris dan kolom yang tetap. Perkalian matriks merupakan desain perkalian yang penting dalam komputasi paralel. Di sini kita akan membahas implementasi perkalian matriks pada berbagai jaringan komunikasi seperti mesh dan hypercube. Mesh dan hypercube memiliki konektivitas jaringan yang lebih tinggi, sehingga memungkinkan algoritme yang lebih cepat daripada jaringan lain seperti jaringan ring.

Jaringan Mesh

Topologi dimana sekumpulan node membentuk grid berdimensi-p disebut topologi mesh. Di sini, semua tepi sejajar dengan sumbu kisi dan semua node yang berdekatan dapat berkomunikasi satu sama lain.

Jumlah total node = (jumlah node dalam baris) × (jumlah node dalam kolom)

Jaringan mesh dapat dievaluasi menggunakan faktor-faktor berikut -

Diameter
Lebar biseksi

Diameter - Dalam jaringan mesh, terpanjang distanceantara dua node adalah diameternya. Memiliki jaringan mesh berdimensi-pkP node memiliki diameter p(k–1).

Bisection width - Lebar biseksi adalah jumlah minimum tepi yang perlu dikeluarkan dari jaringan untuk membagi jaringan mata jaring menjadi dua bagian.

Perkalian Matriks Menggunakan Jaringan Mesh

Kami telah mempertimbangkan model SIMD jaringan mesh 2D yang memiliki koneksi sampul. Kami akan merancang algoritma untuk mengalikan dua array nxn menggunakan n ² prosesor dalam jumlah waktu tertentu.

Matriks A dan B masing-masing memiliki unsur a _ij dan b _ij . Elemen pemrosesan PE _ij mewakili a _ij dan b _ij . Susunlah matriks A dan B sedemikian rupa sehingga setiap prosesor memiliki sepasang elemen untuk dikalikan. Unsur-unsur matriks A akan bergerak ke arah kiri dan unsur-unsur matriks B akan bergerak ke arah atas. Perubahan posisi elemen dalam matriks A dan B ini menghadirkan setiap elemen pemrosesan, PE, pasangan nilai baru untuk dikalikan.

Langkah-langkah dalam Algoritma

Buat dua matriks berbeda-beda.
Hitung semua hasil kali, a _ik × b _kj
Hitung jumlah saat langkah 2 selesai.

Algoritma

Procedure MatrixMulti

Begin
   for k = 1 to n-1
	
   for all Pij; where i and j ranges from 1 to n
      ifi is greater than k then
         rotate a in left direction
      end if
		
   if j is greater than k then
      rotate b in the upward direction
   end if
	
   for all Pij ; where i and j lies between 1 and n
      compute the product of a and b and store it in c
   for k= 1 to n-1 step 1
   for all Pi;j where i and j ranges from 1 to n
      rotate a in left direction
      rotate b in the upward direction
      c=c+aXb
End

Jaringan Hypercube

Hypercube adalah konstruksi berdimensi-n yang ujung-ujungnya tegak lurus satu sama lain dan memiliki panjang yang sama. Hiperkub berdimensi-n juga dikenal sebagai kubus-n atau kubus berdimensi-n.

Fitur Hypercube dengan node 2 ^k

Diameter = k
Lebar biseksi = 2 ^{k – 1}
Jumlah tepi = k

Perkalian Matriks menggunakan Jaringan Hypercube

Spesifikasi umum jaringan Hypercube -

Membiarkan N = 2^mmenjadi jumlah prosesor. Biarkan prosesor menjadi P _0, P ₁ … ..P _N-1 .
Misalkan i dan i ^b adalah dua bilangan bulat, 0 <i, i ^b <N-1 dan representasi binernya hanya berbeda pada posisi b, 0 <b <k – 1.
Mari kita pertimbangkan dua matriks n × n, matriks A dan matriks B.
Step 1- Elemen matriks A dan matriks B ditempatkan ^pada prosesor n ³ sedemikian rupa sehingga prosesor pada posisi i, j, k akan memiliki a _ji dan b _ik .
Step 2 - Semua prosesor dalam posisi (i, j, k) menghitung produk

C (i, j, k) = A (i, j, k) × B (i, j, k)
Step 3 - Jumlah C (0, j, k) = ΣC (i, j, k) untuk 0 ≤ i ≤ n-1, dimana 0 ≤ j, k <n – 1.

Blok Matriks

Block Matrix atau matriks yang dipartisi adalah matriks yang setiap elemennya merepresentasikan matriks individu. Bagian individual ini dikenal sebagai ablock atau sub-matrix.

Contoh

Pada Gambar (a), X adalah matriks blok dimana A, B, C, D adalah matriks itu sendiri. Gambar (f) menunjukkan matriks total.

Perkalian Matriks Blok

Jika dua matriks blok adalah matriks persegi, maka matriks tersebut dikalikan seperti kita melakukan perkalian matriks sederhana. Sebagai contoh,

Sortasi adalah proses menyusun elemen-elemen dalam suatu kelompok dalam urutan tertentu, yaitu urutan menaik, urutan turun, urutan abjad, dll. Berikut ini kita akan bahas -

Urutan Pencacahan
Urutan Transposisi Genap-Ganjil
Urutan Gabungan Paralel
Urutan Cepat Hyper

Menyortir daftar elemen adalah operasi yang sangat umum. Algoritme pengurutan berurutan mungkin tidak cukup efisien ketika kita harus mengurutkan data dalam jumlah besar. Oleh karena itu, algoritma paralel digunakan dalam pengurutan.

Urutan Pencacahan

Enumeration sort adalah metode menyusun semua elemen dalam daftar dengan mencari posisi akhir setiap elemen dalam daftar yang diurutkan. Ini dilakukan dengan membandingkan setiap elemen dengan semua elemen lainnya dan menemukan jumlah elemen yang memiliki nilai lebih kecil.

Oleh karena itu, untuk dua elemen, a _i dan a _j, salah satu kasus berikut harus benar -

a _i <a _j
a _i > a _j
a _i = a _j

Algoritma

procedure ENUM_SORTING (n)

begin
   for each process P_1,j do
      C[j] := 0;
		
   for each process P_{i, j} do
	
      if (A[i] < A[j]) or A[i] = A[j] and i < j) then
         C[j] := 1;
      else
         C[j] := 0;
			
   for each process P1, j do
      A[C[j]] := A[j];
		
end ENUM_SORTING

Urutan Transposisi Genap-Ganjil

Urutan Transposisi Genap-Ganjil didasarkan pada teknik Jenis Gelembung. Ini membandingkan dua nomor yang berdekatan dan mengubahnya, jika nomor pertama lebih besar dari nomor kedua untuk mendapatkan daftar urutan naik. Kasus sebaliknya berlaku untuk rangkaian urutan turun. Jenis transposisi Genap-Ganjil beroperasi dalam dua fase -odd phase dan even phase. Dalam kedua fase tersebut, proses pertukaran nomor dengan nomor yang berdekatan di sebelah kanan.

Algoritma

procedure ODD-EVEN_PAR (n) 

begin 
   id := process's label 
	
   for i := 1 to n do 
   begin 
	
      if i is odd and id is odd then 
         compare-exchange_min(id + 1); 
      else 
         compare-exchange_max(id - 1);
			
      if i is even and id is even then 
         compare-exchange_min(id + 1); 
      else 
         compare-exchange_max(id - 1);
			
   end for
	
end ODD-EVEN_PAR

Urutan Gabungan Paralel

Gabungkan pengurutan pertama-tama membagi daftar yang tidak diurutkan menjadi sub-daftar terkecil, membandingkannya dengan daftar yang berdekatan, dan menggabungkannya dalam urutan yang diurutkan. Ini mengimplementasikan paralelisme dengan sangat baik dengan mengikuti algoritma divide and conquer.

Algoritma

procedureparallelmergesort(id, n, data, newdata)

begin
   data = sequentialmergesort(data)
	
      for dim = 1 to n
         data = parallelmerge(id, dim, data)
      endfor
		
   newdata = data
end

Urutan Cepat Hyper

Hyper quick sort adalah implementasi pengurutan cepat pada hypercube. Langkah-langkahnya adalah sebagai berikut -

Bagilah daftar yang tidak diurutkan di antara setiap node.
Urutkan setiap node secara lokal.
Dari node 0, siarkan nilai median.
Pisahkan setiap daftar secara lokal, lalu tukarkan bagiannya di dimensi tertinggi.
Ulangi langkah 3 dan 4 secara paralel hingga dimensinya mencapai 0.

Algoritma

procedure HYPERQUICKSORT (B, n)
begin

   id := process’s label;
	
   for i := 1 to d do
      begin
      x := pivot;
      partition B into B1 and B2 such that B1 ≤ x < B2;
      if ith bit is 0 then
		
      begin
         send B2 to the process along the ith communication link;
         C := subsequence received along the ith communication link;
         B := B1 U C;
      endif
      
      else
         send B1 to the process along the ith communication link;
         C := subsequence received along the ith communication link;
         B := B2 U C;
         end else
      end for
		
   sort B using sequential quicksort;
	
end HYPERQUICKSORT

Pencarian adalah salah satu operasi fundamental dalam ilmu komputer. Ini digunakan di semua aplikasi di mana kita perlu menemukan apakah suatu elemen ada dalam daftar yang diberikan atau tidak. Pada bab ini, kita akan membahas algoritma pencarian berikut -

Memecah dan menaklukkan
Penelusuran Kedalaman-Pertama
Pencarian Luas-Pertama
Pencarian Terbaik-Pertama

Memecah dan menaklukkan

Pendekatan divide and conquer melibatkan langkah-langkah berikut di setiap level -

Divide - Masalah asli dibagi menjadi sub-sub masalah.
Conquer - Sub-masalah diselesaikan secara rekursif.
Combine - Solusi dari sub masalah digabungkan untuk mendapatkan solusi dari masalah aslinya.

Pencarian biner adalah contoh algoritma divide and conquer.

Pseudocode

Binarysearch(a, b, low, high)

if low < high then
   return NOT FOUND
else
   mid ← (low+high) / 2
   if b = key(mid) then
      return key(mid)
   else if b < key(mid) then
      return BinarySearch(a, b, low, mid−1)
   else
   
      return BinarySearch(a, b, mid+1, high)

Penelusuran Kedalaman-Pertama

Depth-First Search (atau DFS) adalah algoritma untuk mencari pohon atau struktur data grafik yang tidak diarahkan. Di sini, konsepnya dimulai dari simpul awal yang dikenal sebagairootdan melintasi sejauh mungkin di cabang yang sama. Jika kita mendapatkan simpul tanpa simpul penerus, kita kembali dan melanjutkan dengan simpul, yang belum dikunjungi.

Langkah-langkah Penelusuran Mendalam-Pertama

Pertimbangkan node (root) yang tidak dikunjungi sebelumnya dan tandai sebagai dikunjungi.
Kunjungi node penerus pertama yang berdekatan dan tandai sebagai dikunjungi.
Jika semua node penerus dari node yang dipertimbangkan sudah dikunjungi atau tidak memiliki node penerus lagi, kembali ke node induknya.

Pseudocode

Membiarkan v menjadi puncak di mana pencarian dimulai pada Grafik G.

DFS(G,v)

   Stack S := {};
	
   for each vertex u, set visited[u] := false;
   push S, v;
   while (S is not empty) do
     u := pop S;
	  
      if (not visited[u]) then
         visited[u] := true;
         for each unvisited neighbour w of u
            push S, w;
      end if
		
   end while
   
END DFS()

Pencarian Luas-Pertama

Breadth-First Search (atau BFS) adalah algoritma untuk mencari pohon atau struktur data grafik yang tidak diarahkan. Di sini, kita mulai dengan sebuah node dan kemudian mengunjungi semua node yang berdekatan di tingkat yang sama dan kemudian pindah ke node penerus yang berdekatan di tingkat berikutnya. Ini juga dikenal sebagailevel-by-level search.

Langkah-Langkah Pencarian Luas-Pertama

Mulailah dengan simpul akar, tandai itu dikunjungi.
Karena node root tidak memiliki node di level yang sama, lanjutkan ke level berikutnya.
Kunjungi semua node yang berdekatan dan tandai sebagai dikunjungi.
Pergi ke tingkat berikutnya dan kunjungi semua node berdekatan yang belum dikunjungi.
Lanjutkan proses ini sampai semua node dikunjungi.

Pseudocode

Membiarkan v menjadi puncak di mana pencarian dimulai pada Grafik G.

BFS(G,v)

   Queue Q := {};
	
   for each vertex u, set visited[u] := false;
   insert Q, v;
   while (Q is not empty) do
      u := delete Q;
		
      if (not visited[u]) then
         visited[u] := true;
         for each unvisited neighbor w of u
            insert Q, w;
      end if
		
   end while
   
END BFS()

Pencarian Terbaik-Pertama

Best-First Search adalah algoritme yang melintasi grafik untuk mencapai target di jalur yang sesingkat mungkin. Tidak seperti BFS dan DFS, Best-First Search mengikuti fungsi evaluasi untuk menentukan node mana yang paling tepat untuk dilintasi berikutnya.

Langkah-Langkah Pencarian Terbaik-Pertama

Mulailah dengan simpul akar, tandai itu dikunjungi.
Temukan node yang sesuai berikutnya dan tandai sebagai dikunjungi.
Pergi ke tingkat berikutnya dan temukan node yang sesuai dan tandai sebagai dikunjungi.
Lanjutkan proses ini hingga target tercapai.

Pseudocode

BFS( m )

   Insert( m.StartNode )
   Until PriorityQueue is empty
      c ← PriorityQueue.DeleteMin
      If c is the goal
      Exit
   Else
   
      Foreach neighbor n of c
         If n "Unvisited"
            Mark n "Visited"
            Insert( n )
      Mark c "Examined"
      
End procedure

Grafik adalah notasi abstrak yang digunakan untuk merepresentasikan hubungan antar pasangan objek. Grafik terdiri dari -

Vertices- Objek yang saling berhubungan dalam grafik disebut simpul. Simpul juga dikenal sebagainodes.
Edges - Tepi adalah penghubung yang menghubungkan simpul.

Ada dua jenis grafik -

Directed graph - Pada graf berarah, sisi-sisi memiliki arah, yaitu sisi-sisi berpindah dari satu simpul ke simpul lainnya.
Undirected graph - Pada graf tidak berarah, tepi tidak memiliki arah.

Pewarnaan Grafik

Pewarnaan graf adalah metode untuk menetapkan warna pada simpul dari sebuah graf sehingga tidak ada dua simpul yang berdekatan memiliki warna yang sama. Beberapa masalah pewarnaan grafik adalah -

Vertex coloring - Cara mewarnai simpul dari grafik sehingga tidak ada dua simpul yang berdekatan memiliki warna yang sama.
Edge Coloring - Ini adalah metode pemberian warna ke setiap tepi sehingga tidak ada dua tepi yang berdekatan memiliki warna yang sama.
Face coloring - Ini memberikan warna untuk setiap permukaan atau wilayah dari grafik planar sehingga tidak ada dua permukaan yang berbagi batas yang sama memiliki warna yang sama.

Nomor Chromatic

Bilangan kromatik adalah jumlah warna minimum yang dibutuhkan untuk mewarnai grafik. Misalnya, bilangan kromatik dari grafik berikut adalah 3.

Konsep pewarnaan graf diterapkan dalam penyusunan jadwal, penetapan frekuensi radio bergerak, suduku, alokasi register, dan pewarnaan peta.

Langkah-langkah pewarnaan grafik

Tetapkan nilai awal setiap prosesor dalam larik berdimensi-n ke 1.
Sekarang untuk menetapkan warna tertentu ke simpul, tentukan apakah warna itu sudah ditetapkan ke simpul yang berdekatan atau belum.
Jika prosesor mendeteksi warna yang sama di simpul yang berdekatan, itu menetapkan nilainya dalam larik ke 0.
Setelah membuat n ² perbandingan, jika ada elemen dari array yang bernilai 1, maka itu adalah pewarnaan yang valid.

Pseudocode untuk pewarnaan grafik

begin

   create the processors P(i₀,i₁,...i_n-1) where 0_i_v < m, 0 _ v < n
   status[i0,..i_n-1] = 1
	
   for j varies from 0 to n-1 do
      begin
		
         for k varies from 0 to n-1 do
         begin
            if a_j,k=1 and i_j=i_kthen
            status[i₀,..i_n-1] =0
         end
			
      end
      ok = ΣStatus
		
   if ok > 0, then display valid coloring exists
   else
      display invalid coloring
      
end

Minimal Spanning Tree

Pohon bentang yang jumlah berat (atau panjang) semua tepinya kurang dari semua pohon bentang lain yang mungkin dari grafik G dikenal sebagai a minimal spanning tree atau minimum cost spanningpohon. Gambar berikut menunjukkan grafik terhubung berbobot.

Beberapa pohon rentang yang mungkin dari grafik di atas ditunjukkan di bawah -

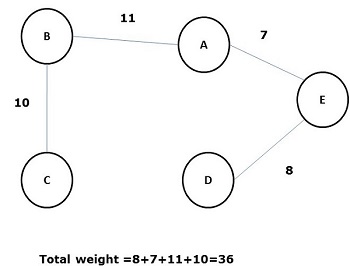
Di antara semua pohon bentang di atas, gambar (d) adalah pohon bentang minimum. Konsep pohon rentang biaya minimum diterapkan dalam masalah travelling salesman, merancang sirkuit elektronik, Merancang jaringan yang efisien, dan merancang algoritma perutean yang efisien.

Untuk mengimplementasikan pohon rentang biaya minimum, dua metode berikut digunakan -

Algoritma Prim
Algoritma Kruskal

Algoritma Prim

Algoritme Prim adalah algoritme serakah, yang membantu kita menemukan pohon rentang minimum untuk grafik tak berarah berbobot. Ia memilih sebuah simpul terlebih dahulu dan menemukan sebuah sisi dengan kejadian bobot terendah pada simpul tersebut.

Langkah-langkah Algoritma Prim

Pilih sembarang titik, ucapkan v ₁ dari Grafik G.
Pilih satu sisi, katakanlah e ₁ dari G sehingga e ₁ = v ₁ v ₂ dan v ₁ ≠ v ₂ dan e ₁ memiliki bobot minimum di antara sisi-sisi yang bersisian pada v ₁ dalam grafik G.
Sekarang, mengikuti langkah 2, pilih insiden tepi berbobot minimum pada v ₂ .
Lanjutkan ini sampai n – 1 tepi telah dipilih. Sinin adalah jumlah simpul.

Pohon rentang minimum adalah -

Algoritma Kruskal

Algoritme Kruskal adalah algoritme serakah, yang membantu kita menemukan pohon rentang minimum untuk grafik berbobot yang terhubung, menambahkan busur biaya yang meningkat di setiap langkah. Ini adalah algoritma pohon perentang minimum yang menemukan tepi dengan bobot sekecil mungkin yang menghubungkan dua pohon di hutan.

Langkah-langkah Algoritma Kruskal

Pilih tepi dengan berat minimum; katakanlah e ₁ dari Grafik G dan e ₁ bukan sebuah loop.
Pilih tepi berbobot minimum berikutnya yang terhubung ke e ₁ .
Lanjutkan ini sampai n – 1 tepi telah dipilih. Sinin adalah jumlah simpul.

Pohon rentang minimum dari grafik di atas adalah -

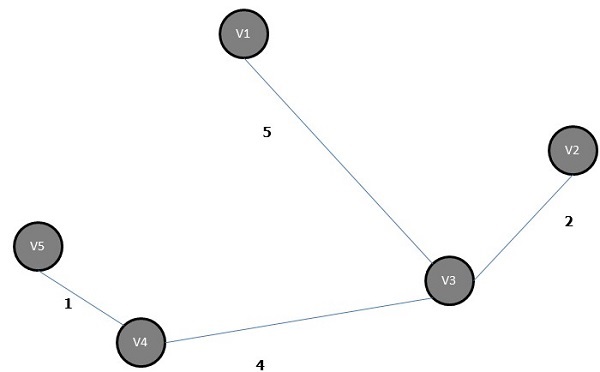
Algoritma Jalur Terpendek

Algoritma Shortest Path adalah metode untuk mencari jalur dengan biaya terkecil dari node sumber (S) ke node tujuan (D). Di sini, kita akan membahas algoritma Moore, juga dikenal sebagai Algoritma Pencarian Pertama Luas.

Algoritme Moore

Beri label simpul sumber, S dan beri label i dan set i=0.
Temukan semua simpul tak berlabel yang berdekatan dengan simpul berlabel i. Jika tidak ada simpul yang terhubung ke simpul, S, maka simpul, D, tidak terhubung ke S. Jika ada simpul terhubung ke S, beri labeli+1.
Jika D diberi label, lanjutkan ke langkah 4, jika tidak lanjutkan ke langkah 2 untuk meningkatkan i = i + 1.
Berhenti setelah panjang jalan terpendek ditemukan.

Algoritma Paralel - Panduan Cepat

Pemrosesan Bersamaan

Apa itu Paralelisme?

Apa itu Algoritma?

Model Komputasi

Komputer SISD

Komputer SIMD

Komputer MISD

Komputer MIMD

Catatan

Kompleksitas Waktu

Analisis Asymptotic

Notasi Big O

Notasi omega

Notasi Theta

Mempercepat Algoritma

Jumlah Prosesor yang Digunakan

Total biaya

Data Paralel

Model Grafik Tugas

Model Kolam Kerja

Model Master-Budak

Tindakan pencegahan dalam menggunakan model master-slave

Model Pipa

Model Hibrida

Model Memori Bersama

Manfaat Pemrograman Memori Bersama

Kekurangan Pemrograman Memori Bersama

Model Penyampaian Pesan

Komunikasi Point-to-Point

Komunikasi Kolektif

Manfaat Pengiriman Pesan

Kekurangan Penyampaian Pesan

Perpustakaan yang Melewati Pesan

Message Passing Interface (MPI)

Mesin Virtual Paralel (PVM)

Pemrograman Data Paralel

Daftar Tertaut

Daftar Tertaut Tunggal

Daftar Tertaut Ganda

Daftar Tertaut Melingkar

Array

Jaringan Hypercube

Metode Pisahkan dan Taklukkan

Metode Serakah

Pemrograman Dinamis

Algoritma Mundur

Branch and Bound

Pemrograman Linear

Jaringan Mesh

Perkalian Matriks Menggunakan Jaringan Mesh

Langkah-langkah dalam Algoritma

Algoritma

Jaringan Hypercube

Fitur Hypercube dengan node 2 k

Perkalian Matriks menggunakan Jaringan Hypercube

Blok Matriks

Contoh

Perkalian Matriks Blok

Urutan Pencacahan

Algoritma

Urutan Transposisi Genap-Ganjil

Algoritma

Urutan Gabungan Paralel

Algoritma

Urutan Cepat Hyper

Algoritma

Memecah dan menaklukkan

Pseudocode

Penelusuran Kedalaman-Pertama

Langkah-langkah Penelusuran Mendalam-Pertama

Pseudocode

Pencarian Luas-Pertama

Langkah-Langkah Pencarian Luas-Pertama

Pseudocode

Pencarian Terbaik-Pertama

Langkah-Langkah Pencarian Terbaik-Pertama

Pseudocode

Pewarnaan Grafik

Nomor Chromatic

Fitur Hypercube dengan node 2 ^k