Merencanakan bilangan rasional pada garis bilangan
Bilangan rasional adalah pecahan dan diplot pada garis bilangan sebagai berikut.
Basic rules of representing rational no. on number line
Jika bilangan rasional (pecahan) tepat maka, itu terletak di antara 0 dan 1.
Jika bilangan rasional (pecahan) tidak tepat maka, pertama-tama kita mengubahnya menjadi pecahan campuran dan kemudian jawaban rasional yang diberikan. terletak di antara bilangan bulat dan bilangan bulat berikutnya.
Kami menggunakan langkah-langkah berikut untuk merepresentasikan bilangan rasional atau pecahan misalnya, $ \ frac {5} {7} $ pada garis bilangan.
Step 1 - Kami menggambar garis bilangan.
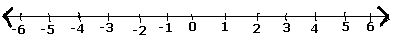
Step 2- Karena bilangan $ \ frac {5} {7} $ adalah bilangan positif, ia terletak di sisi kanan nol.
Step 3- Jadi, setelah tanda nol, kita punya $ \ frac {1} {7}, \: \ frac {2} {7}, \: \ frac {3} {7}, \: \ frac {4} {7 }, \: \ frac {5} {7}, \: \ frac {6} {7}, $ dan ( $ \ frac {7} {7} $ = 1).
Step 4- Bilangan rasional $ \ frac {5} {7} $ pada garis bilangan ditampilkan sebagai berikut.

Plot $ \ frac {1} {4} $ dan $ 1 \ frac {2} {4} $ pada baris bilangan di bawah ini
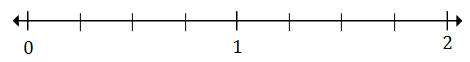
Larutan
Step 1:
$ \ frac {1} {4} $ (A) terletak di antara 0 dan 1; $ 1 \ frac {2} {4} $ (B) terletak di antara 1 dan 2
Step 2:
Setiap divisi dibagi menjadi empat bagian karena bagian bawah pecahannya adalah 4.
$ \ frac {1} {4} $ adalah tanda pertama setelah 0, oleh karena itu titik A mewakili $ \ frac {1} {4} $
$ 1 \ frac {2} {4} $ adalah tanda kedua setelah 1, jadi titik B mewakili $ 1 \ frac {2} {4} $
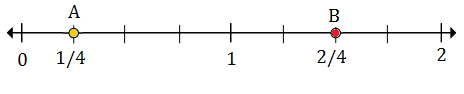
Plot $ \ frac {5} {8} $ dan $ 2 \ frac {3} {8} $ pada baris bilangan di bawah
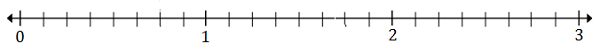
Larutan
Step 1:
$ \ frac {5} {8} $ 8 (A) terletak di antara 0 dan 1; $ 2 \ frac {3} {8} $ (B) terletak di antara 2 dan 3
Step 2:
Setiap divisi dibagi menjadi delapan bagian karena pecahan terbawah adalah 8.
$ \ frac {5} {8} $ adalah tanda kelima setelah 0, oleh karena itu titik A mewakili $ \ frac {5} {8} $
$ 2 \ frac {3} {8} $ adalah tanda ketiga setelah 2, jadi titik B mewakili $ 2 \ frac {3} {8} $
