Komunikasi Satelit - Hukum Kepler

Kita tahu bahwa satelit berputar mengelilingi bumi, yang mirip dengan bumi berputar mengelilingi matahari. Jadi, prinsip yang diterapkan pada bumi dan pergerakannya mengelilingi matahari juga berlaku untuk satelit dan pergerakannya mengelilingi bumi.

Banyak ilmuwan telah memberikan berbagai jenis teori sejak zaman awal. Tapi hanyaJohannes Kepler (1571-1630) adalah salah satu ilmuwan yang paling diterima dalam menjelaskan prinsip satelit yang bergerak mengelilingi bumi.

Kepler merumuskan tiga hukum yang mengubah teori dan observasi komunikasi satelit secara keseluruhan. Ini dikenal sebagaiKepler’s laws. Ini berguna untuk memvisualisasikan gerakan melalui ruang.

Hukum Pertama Kepler

Hukum pertama Kepler menyatakan bahwa jalur yang diikuti oleh satelit di sekitar primernya (bumi) adalah sebuah ellipse. Elips ini memiliki dua titik fokus (foci) F1 dan F2 seperti yang ditunjukkan pada gambar di bawah ini. Pusat massa bumi akan selalu berada di salah satu dari dua fokus elips.

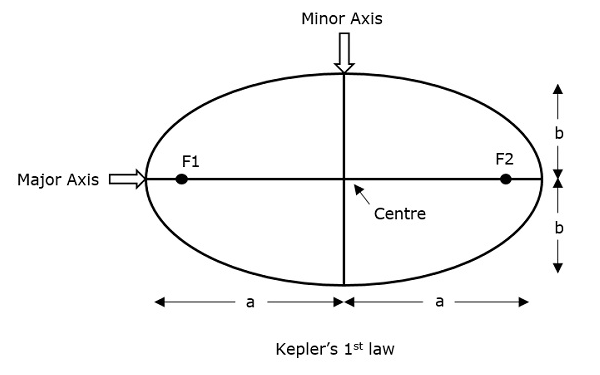
Jika jarak dari pusat benda ke titik pada jalur elipsnya diperhitungkan, maka titik terjauh sebuah elips dari pusat disebut sebagai apogee dan titik terpendek elips dari pusat disebut sebagai perigee.

Eccentricity "e" sistem ini dapat ditulis sebagai -

$$e = \frac{\sqrt{a^2 - b^2}}{a}$$

Dimana, a & b adalah panjang sumbu semi mayor dan sumbu semi minor elips.

Untuk sebuah elliptical path, nilai eksentrisitas (e) selalu berada di antara 0 dan 1, yaitu $0$ < $e$ < $1$, karena a lebih besar dari b. Misalkan nilai eksentrisitas (e) nol, maka jalur tidak lagi berbentuk elips, melainkan akan diubah menjadi bentuk lingkaran.

Hukum Kedua Kepler

Hukum kedua Kepler menyatakan bahwa untuk interval waktu yang sama, the areayang tercakup oleh satelit akan sama sehubungan dengan pusat massa bumi. Hal tersebut dapat dipahami dengan memperhatikan gambar berikut.

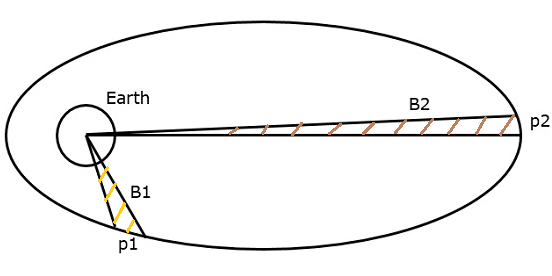
Asumsikan, satelit mencakup jarak p1 dan p2 dalam interval waktu yang sama. Kemudian, area B1 dan B2 yang dicakup oleh satelit pada kedua contoh tersebut adalah sama.

Hukum Ketiga Kepler

Hukum ketiga Kepler menyatakan bahwa, kuadrat waktu periodik orbit elips sebanding dengan pangkat tiga dari panjang sumbu semi mayornya. Mathematically, dapat ditulis sebagai berikut -

$$T^2\:\alpha\:a^3$$

$$=> T^2=\left(\frac{4\pi ^2}{\mu }\right) a^3$$

Dimana, $\frac{4\pi^2}{\mu}$ adalah konstanta proporsionalitas.

$\mu$adalah konstanta Kepler dan nilainya sama dengan 3.986005 x 10 ¹⁴ m ³ / detik ²

$$1 = \left(\frac{2\pi}{T}\right)^2\left(\frac{a^2}{\mu}\right)$$

$$1 = n^2\left(\frac{a^3}{\mu}\right)$$

$$=> a^3 = \frac{\mu}{n^2}$$

Dimana, ‘n’ adalah gerakan rata-rata satelit dalam radian per detik.

Note- Sebuah satelit, ketika berputar mengelilingi bumi, mengalami gaya tarik dari bumi, yaitu gaya gravitasi. Demikian pula, ia mengalami gaya tarikan lain dari matahari dan bulan. Oleh karena itu, satelit harus menyeimbangkan kedua gaya ini agar tetap berada di orbitnya.