TensorFlow - Fondasi Matematika
Penting untuk memahami konsep matematika yang diperlukan untuk TensorFlow sebelum membuat aplikasi dasar di TensorFlow. Matematika dianggap sebagai inti dari semua algoritme pembelajaran mesin. Dengan bantuan konsep inti Matematika, solusi untuk algoritma pembelajaran mesin tertentu ditentukan.
Vektor
Larik angka, yang kontinu atau diskrit, didefinisikan sebagai vektor. Algoritme pembelajaran mesin menangani vektor panjang tetap untuk menghasilkan keluaran yang lebih baik.
Algoritme pembelajaran mesin menangani data multidimensi sehingga vektor memainkan peran penting.

Representasi bergambar model vektor adalah sebagai berikut -
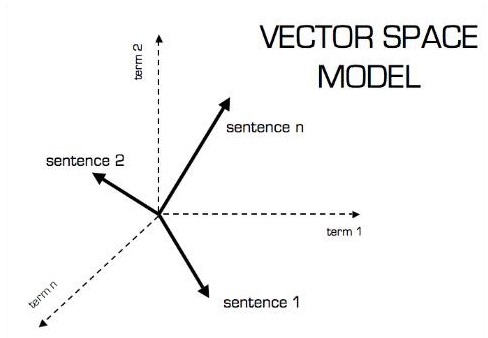
Skalar
Skalar dapat didefinisikan sebagai vektor satu dimensi. Skalar adalah skalar, yang hanya mencakup besaran dan tidak ada arah. Dengan skalar, kami hanya mementingkan besarannya.
Contoh skalar termasuk parameter berat dan tinggi badan anak.
Matriks
Matriks dapat didefinisikan sebagai larik multidimensi, yang disusun dalam format baris dan kolom. Besar kecilnya matriks ditentukan oleh panjang baris dan panjang kolom. Gambar berikut menunjukkan representasi dari matriks tertentu.
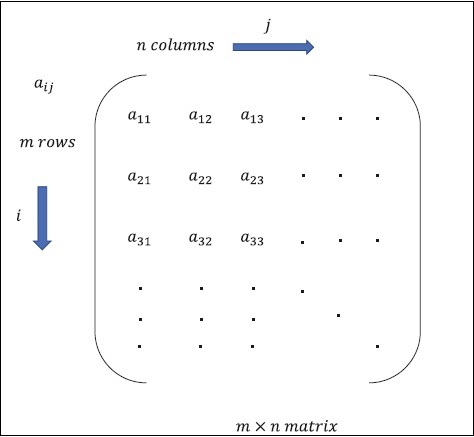
Perhatikan matriks dengan baris “m” dan kolom “n” seperti yang disebutkan di atas, representasi matriks akan ditentukan sebagai “matriks m * n” yang juga mendefinisikan panjang matriks.
Perhitungan Matematika
Pada bagian ini, kita akan mempelajari tentang Perhitungan Matematika yang berbeda di TensorFlow.
Penambahan matriks
Penambahan dua atau lebih matriks dimungkinkan jika matriks-matriks tersebut memiliki dimensi yang sama. Penambahan menyiratkan penambahan setiap elemen sesuai posisi yang diberikan.
Perhatikan contoh berikut untuk memahami cara kerja penambahan matriks -
$$ Contoh: A = \ begin {bmatrix} 1 & 2 \\ 3 & 4 \ end {bmatrix} B = \ begin {bmatrix} 5 & 6 \\ 7 & 8 \ end {bmatrix} \: kemudian \: A + B = \ begin {bmatrix} 1 + 5 & 2 + 6 \\ 3 + 7 & 4 + 8 \ end {bmatrix} = \ begin {bmatrix} 6 & 8 \\ 10 & 12 \ end {bmatrix} $$
Pengurangan matriks
Pengurangan matriks beroperasi dengan cara yang sama seperti penjumlahan dua matriks. Pengguna dapat mengurangi dua matriks asalkan dimensinya sama.
$$ Contoh: A- \ begin {bmatrix} 1 & 2 \\ 3 & 4 \ end {bmatrix} B- \ begin {bmatrix} 5 & 6 \\ 7 & 8 \ end {bmatrix} \: kemudian \: AB - \ begin {bmatrix} 1-5 & 2-6 \\ 3-7 & 4-8 \ end {bmatrix} - \ begin {bmatrix} -4 & -4 \\ - 4 & -4 \ end {bmatrix} $$
Perkalian matriks
Agar dua matriks A m * n dan B p * q dapat dikalikan, n harus sama dengan p. Matriks yang dihasilkan adalah -
C m * q
$$ A = \ begin {bmatrix} 1 & 2 \\ 3 & 4 \ end {bmatrix} B = \ begin {bmatrix} 5 & 6 \\ 7 & 8 \ end {bmatrix} $$
$$ c_ {11} = \ begin {bmatrix} 1 & 2 \ end {bmatrix} \ begin {bmatrix} 5 \\ 7 \ end {bmatrix} = 1 \ times5 + 2 \ times7 = 19 \: c_ {12} = \ begin {bmatrix} 1 & 2 \ end {bmatrix} \ begin {bmatrix} 6 \\ 8 \ end {bmatrix} = 1 \ times6 + 2 \ times8 = 22 $$
$$ c_ {21} = \ begin {bmatrix} 3 & 4 \ end {bmatrix} \ begin {bmatrix} 5 \\ 7 \ end {bmatrix} = 3 \ times5 + 4 \ times7 = 43 \: c_ {22} = \ begin {bmatrix} 3 & 4 \ end {bmatrix} \ begin {bmatrix} 6 \\ 8 \ end {bmatrix} = 3 \ times6 + 4 \ times8 = 50 $$
$$ C = \ begin {bmatrix} c_ {11} & c_ {12} \\ c_ {21} & c_ {22} \ end {bmatrix} = \ begin {bmatrix} 19 & 22 \\ 43 & 50 \ end {bmatrix} $$
Ubah urutan matriks
Transposisi matriks A, m * n umumnya diwakili oleh AT (transpos) n * m dan diperoleh dengan mentransposisi vektor kolom sebagai vektor baris.
$$ Contoh: A = \ begin {bmatrix} 1 & 2 \\ 3 & 4 \ end {bmatrix} \: kemudian \: A ^ {T} \ begin {bmatrix} 1 & 3 \\ 2 & 4 \ end { bmatrix} $$
Perkalian titik dari vektor
Setiap vektor berdimensi n dapat direpresentasikan sebagai matriks v = R ^ n * 1.
$$ v_ {1} = \ begin {bmatrix} v_ {11} \\ v_ {12} \\\ cdot \\\ cdot \\\ cdot \\ v_ {1n} \ end {bmatrix} v_ {2} = \ begin {bmatrix} v_ {21} \\ v_ {22} \\\ cdot \\\ cdot \\\ cdot \\ v_ {2n} \ end {bmatrix} $$
Perkalian titik dari dua vektor adalah jumlah dari perkalian komponen yang bersesuaian - Komponen sepanjang dimensi yang sama dan dapat dinyatakan sebagai
$$ v_ {1} \ cdot v_ {2} = v_1 ^ Tv_ {2} = v_2 ^ Tv_ {1} = v_ {11} v_ {21} + v_ {12} v_ {22} + \ cdot \ cdot + v_ {1n} v_ {2n} = \ displaystyle \ jumlah \ batas_ {k = 1} ^ n v_ {1k} v_ {2k} $$
Contoh perkalian titik dari vektor disebutkan di bawah ini -
$$ Contoh: v_ {1} = \ begin {bmatrix} 1 \\ 2 \\ 3 \ end {bmatrix} v_ {2} = \ begin {bmatrix} 3 \\ 5 \\ - 1 \ end {bmatrix} v_ {1} \ cdot v_ {2} = v_1 ^ Tv_ {2} = 1 \ times3 + 2 \ times5-3 \ times1 = 10 $$