Trasformazione del livello di grigio

Abbiamo discusso alcune delle trasformazioni di base nel nostro tutorial sulla trasformazione di base. In questo tutorial vedremo alcune delle trasformazioni di base del livello di grigio.

Miglioramento dell'immagine

Il miglioramento di un'immagine fornisce un contrasto migliore e un'immagine più dettagliata rispetto a un'immagine non migliorata. Il miglioramento dell'immagine ha molte applicazioni. Viene utilizzato per migliorare le immagini mediche, le immagini acquisite con il telerilevamento, le immagini dal satellite, ecc

La funzione di trasformazione è stata data di seguito

s = T (r)

dove r è i pixel dell'immagine in ingresso es è i pixel dell'immagine in uscita. T è una funzione di trasformazione che mappa ogni valore di r su ogni valore di s. Il miglioramento dell'immagine può essere effettuato tramite trasformazioni del livello di grigio che vengono discusse di seguito.

Trasformazione del livello di grigio

Ci sono tre trasformazioni di base del livello di grigio.

Linear
Logarithmic
Potere - legge

Il grafico generale di queste transizioni è stato mostrato di seguito.

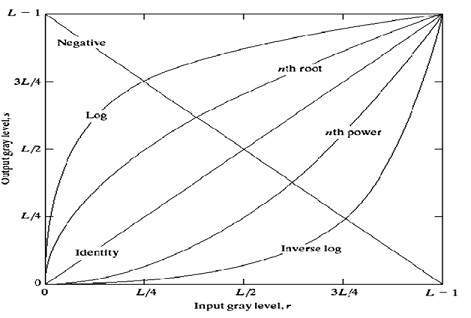
Trasformazione lineare

Per prima cosa esamineremo la trasformazione lineare. La trasformazione lineare include identità semplice e trasformazione negativa. La trasformazione dell'identità è stata discussa nel nostro tutorial sulla trasformazione dell'immagine, ma qui è stata fornita una breve descrizione di questa trasformazione.

La transizione dell'identità è indicata da una linea retta. In questa transizione, ogni valore dell'immagine di input viene mappato direttamente a ogni altro valore dell'immagine di output. Ciò si traduce nella stessa immagine di input e immagine di output. E quindi si chiama trasformazione dell'identità. È stato mostrato di seguito:

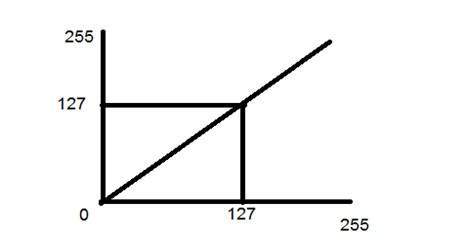
Trasformazione negativa

La seconda trasformazione lineare è la trasformazione negativa, che è invertita della trasformazione dell'identità. Nella trasformazione negativa, ogni valore dell'immagine di input viene sottratto da L-1 e mappato sull'immagine di output.

Il risultato è un po 'come questo.

Immagine in ingresso

Immagine di output

In questo caso è stata eseguita la seguente transizione.

s = (L - 1) - r

poiché l'immagine in ingresso di Einstein è un'immagine a 8 bpp, quindi il numero di livelli in questa immagine è 256. Mettendo 256 nell'equazione, otteniamo questo

s = 255 - r

Quindi ogni valore viene sottratto da 255 e l'immagine del risultato è stata mostrata sopra. Quindi quello che succede è che i pixel più chiari diventano scuri e l'immagine più scura diventa chiara. E si traduce in un'immagine negativa.

È stato mostrato nel grafico sottostante.

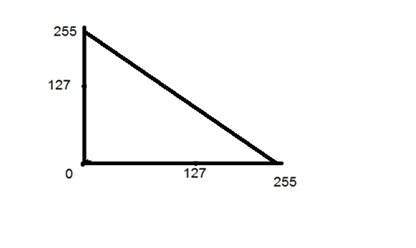
Trasformazioni logaritmiche

La trasformazione logaritmica contiene inoltre due tipi di trasformazione. Trasformazione logaritmica e trasformazione logaritmica inversa.

Trasformazione del registro

Le trasformazioni log possono essere definite da questa formula

s = c log (r + 1).

Dove se r sono i valori dei pixel dell'output e dell'immagine in ingresso ec è una costante. Il valore 1 viene aggiunto a ciascuno dei valori in pixel dell'immagine in ingresso perché se nell'immagine è presente un'intensità di pixel pari a 0, allora log (0) è uguale a infinito. Quindi viene aggiunto 1, per rendere il valore minimo almeno 1.

Durante la trasformazione del registro, i pixel scuri in un'immagine vengono espansi rispetto ai valori dei pixel più alti. I valori dei pixel più alti sono in qualche modo compressi nella trasformazione del registro. Ciò si traduce nel seguente miglioramento dell'immagine.

Il valore di c nella trasformazione del registro regola il tipo di miglioramento che stai cercando.

Immagine in ingresso

Log Tranform Image

La trasformazione logaritmica inversa è opposta alla trasformazione logaritmica.

Potere - Trasformazioni di legge

Ci sono altre due trasformazioni: trasformazioni della legge di potere, che includono l'ennesimo potere e l'ennesima trasformazione della radice. Queste trasformazioni possono essere date dall'espressione:

s = cr ^ γ

Questo simbolo γ è chiamato gamma, a causa del quale questa trasformazione è anche nota come trasformazione gamma.

La variazione del valore di γ varia il miglioramento delle immagini. Diversi dispositivi di visualizzazione / monitor hanno la propria correzione gamma, ecco perché visualizzano la loro immagine con intensità diverse.

Questo tipo di trasformazione viene utilizzato per migliorare le immagini per diversi tipi di dispositivi di visualizzazione. La gamma dei diversi dispositivi di visualizzazione è diversa. Ad esempio, la gamma di CRT è compresa tra 1,8 e 2,5, il che significa che l'immagine visualizzata su CRT è scura.