Keras - Rete neurale di convoluzione

Modifichiamo il modello da MPL a Convolution Neural Network (CNN) per il nostro precedente problema di identificazione delle cifre.

La CNN può essere rappresentata come di seguito:

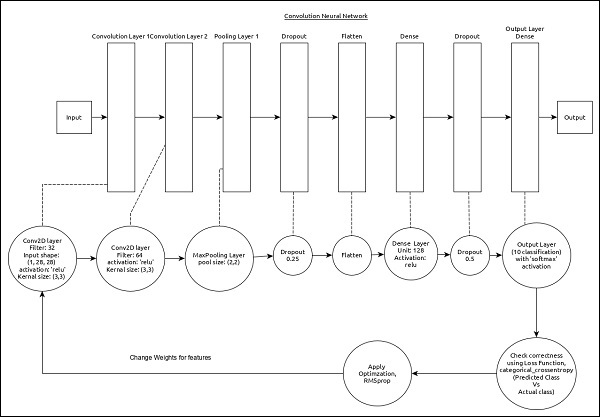
Le caratteristiche principali del modello sono le seguenti:

Il livello di input è costituito da (1, 8, 28) valori.
Primo strato, Conv2D consiste di 32 filtri e funzione di attivazione 'relu' con dimensione del kernel, (3,3).
Secondo strato, Conv2D consiste di 64 filtri e della funzione di attivazione 'relu' con dimensione del kernel, (3,3).
Terzo strato, MaxPooling ha una dimensione della piscina di (2, 2).
Quinto strato, Flatten viene utilizzato per appiattire tutto il suo input in una singola dimensione.
Sesto strato, Dense consiste di 128 neuroni e funzione di attivazione "relu".
Settimo strato, Dropout ha 0,5 come valore.
L'ottavo e ultimo strato è costituito da 10 neuroni e dalla funzione di attivazione "softmax".
Uso categorical_crossentropy come funzione di perdita.
Uso Adadelta() come ottimizzatore.
Uso accuracy come metriche.
Usa 128 come dimensione batch.
Usa 20 come epoche.

Step 1 − Import the modules

Importiamo i moduli necessari.

import keras 
from keras.datasets import mnist 
from keras.models import Sequential 
from keras.layers import Dense, Dropout, Flatten 
from keras.layers import Conv2D, MaxPooling2D 
from keras import backend as K 
import numpy as np

Step 2 − Load data

Importiamo il dataset mnist.

(x_train, y_train), (x_test, y_test) = mnist.load_data()

Step 3 − Process the data

Cambiamo il set di dati in base al nostro modello, in modo che possa essere inserito nel nostro modello.

img_rows, img_cols = 28, 28 

if K.image_data_format() == 'channels_first': 
   x_train = x_train.reshape(x_train.shape[0], 1, img_rows, img_cols) 
   x_test = x_test.reshape(x_test.shape[0], 1, img_rows, img_cols) 
   input_shape = (1, img_rows, img_cols) 
else: 
   x_train = x_train.reshape(x_train.shape[0], img_rows, img_cols, 1) 
   x_test = x_test.reshape(x_test.shape[0], img_rows, img_cols, 1) 
   input_shape = (img_rows, img_cols, 1) 
   
x_train = x_train.astype('float32') 
x_test = x_test.astype('float32') 
x_train /= 255 
x_test /= 255 

y_train = keras.utils.to_categorical(y_train, 10) 
y_test = keras.utils.to_categorical(y_test, 10)

L'elaborazione dei dati è simile al modello MPL tranne la forma dei dati di input e la configurazione del formato dell'immagine.

Step 4 − Create the model

Creiamo il modello reale.

model = Sequential() 
model.add(Conv2D(32, kernel_size = (3, 3),  
   activation = 'relu', input_shape = input_shape)) 
model.add(Conv2D(64, (3, 3), activation = 'relu')) 
model.add(MaxPooling2D(pool_size = (2, 2))) 
model.add(Dropout(0.25)) model.add(Flatten()) 
model.add(Dense(128, activation = 'relu')) 
model.add(Dropout(0.5)) 
model.add(Dense(10, activation = 'softmax'))

Step 5 − Compile the model

Compiliamo il modello utilizzando la funzione di perdita, l'ottimizzatore e le metriche selezionati.

model.compile(loss = keras.losses.categorical_crossentropy, 
   optimizer = keras.optimizers.Adadelta(), metrics = ['accuracy'])

Step 6 − Train the model

Addestriamo il modello usando fit() metodo.

model.fit(
   x_train, y_train, 
   batch_size = 128, 
   epochs = 12, 
   verbose = 1, 
   validation_data = (x_test, y_test)
)

L'esecuzione dell'applicazione produrrà le seguenti informazioni:

Train on 60000 samples, validate on 10000 samples Epoch 1/12 
60000/60000 [==============================] - 84s 1ms/step - loss: 0.2687 
- acc: 0.9173 - val_loss: 0.0549 - val_acc: 0.9827 Epoch 2/12 
60000/60000 [==============================] - 86s 1ms/step - loss: 0.0899 
- acc: 0.9737 - val_loss: 0.0452 - val_acc: 0.9845 Epoch 3/12 
60000/60000 [==============================] - 83s 1ms/step - loss: 0.0666 
- acc: 0.9804 - val_loss: 0.0362 - val_acc: 0.9879 Epoch 4/12 
60000/60000 [==============================] - 81s 1ms/step - loss: 0.0564 
- acc: 0.9830 - val_loss: 0.0336 - val_acc: 0.9890 Epoch 5/12 
60000/60000 [==============================] - 86s 1ms/step - loss: 0.0472 
- acc: 0.9861 - val_loss: 0.0312 - val_acc: 0.9901 Epoch 6/12 
60000/60000 [==============================] - 83s 1ms/step - loss: 0.0414 
- acc: 0.9877 - val_loss: 0.0306 - val_acc: 0.9902 Epoch 7/12 
60000/60000 [==============================] - 89s 1ms/step - loss: 0.0375 
-acc: 0.9883 - val_loss: 0.0281 - val_acc: 0.9906 Epoch 8/12 
60000/60000 [==============================] - 91s 2ms/step - loss: 0.0339 
- acc: 0.9893 - val_loss: 0.0280 - val_acc: 0.9912 Epoch 9/12 
60000/60000 [==============================] - 89s 1ms/step - loss: 0.0325 
- acc: 0.9901 - val_loss: 0.0260 - val_acc: 0.9909 Epoch 10/12 
60000/60000 [==============================] - 89s 1ms/step - loss: 0.0284 
- acc: 0.9910 - val_loss: 0.0250 - val_acc: 0.9919 Epoch 11/12 
60000/60000 [==============================] - 86s 1ms/step - loss: 0.0287 
- acc: 0.9907 - val_loss: 0.0264 - val_acc: 0.9916 Epoch 12/12 
60000/60000 [==============================] - 86s 1ms/step - loss: 0.0265 
- acc: 0.9920 - val_loss: 0.0249 - val_acc: 0.9922

Step 7 − Evaluate the model

Cerchiamo di valutare il modello utilizzando dati di test.

score = model.evaluate(x_test, y_test, verbose = 0) 

print('Test loss:', score[0]) 
print('Test accuracy:', score[1])

L'esecuzione del codice precedente produrrà le informazioni seguenti:

Test loss: 0.024936060590433316 
Test accuracy: 0.9922

La precisione del test è del 99,22%. Abbiamo creato un modello migliore per identificare le cifre della scrittura a mano.

Step 8 − Predict

Infine, prevedere la cifra dalle immagini come di seguito -

pred = model.predict(x_test) 
pred = np.argmax(pred, axis = 1)[:5] 
label = np.argmax(y_test,axis = 1)[:5] 

print(pred) 
print(label)

L'output dell'applicazione di cui sopra è il seguente:

[7 2 1 0 4] 
[7 2 1 0 4]

L'output di entrambi gli array è identico e indica che il nostro modello prevede correttamente le prime cinque immagini.