Algoritmo parallelo - Guida rapida

Un algorithmè una sequenza di passaggi che riceve input dall'utente e, dopo alcuni calcoli, produce un output. UNparallel algorithm è un algoritmo che può eseguire più istruzioni contemporaneamente su diversi dispositivi di elaborazione e quindi combinare tutte le singole uscite per produrre il risultato finale.

Elaborazione simultanea

La facile disponibilità di computer insieme alla crescita di Internet ha cambiato il modo in cui archiviamo ed elaboriamo i dati. Viviamo in un'epoca in cui i dati sono disponibili in abbondanza. Ogni giorno trattiamo enormi volumi di dati che richiedono elaborazioni complesse e anche questo, in tempi rapidi. A volte, abbiamo bisogno di recuperare dati da eventi simili o correlati che si verificano simultaneamente. Questo è dove abbiamo bisognoconcurrent processing che può dividere un compito complesso ed elaborarlo su più sistemi per produrre l'output in tempi rapidi.

L'elaborazione simultanea è essenziale quando l'attività comporta l'elaborazione di una massa enorme di dati complessi. Gli esempi includono: accesso a grandi database, test di aeromobili, calcoli astronomici, fisica atomica e nucleare, analisi biomedica, pianificazione economica, elaborazione delle immagini, robotica, previsioni meteorologiche, servizi basati sul web, ecc.

Cos'è il parallelismo?

Parallelismè il processo di elaborazione simultanea di più set di istruzioni. Riduce il tempo di calcolo totale. Il parallelismo può essere implementato utilizzandoparallel computers,cioè un computer con molti processori. I computer paralleli richiedono algoritmi paralleli, linguaggi di programmazione, compilatori e sistemi operativi che supportano il multitasking.

In questo tutorial, parleremo solo di parallel algorithms. Prima di andare oltre, discutiamo prima degli algoritmi e dei loro tipi.

Cos'è un algoritmo?

Un algorithmè una sequenza di istruzioni seguite per risolvere un problema. Durante la progettazione di un algoritmo, dovremmo considerare l'architettura del computer su cui verrà eseguito l'algoritmo. Secondo l'architettura, ci sono due tipi di computer:

• Computer sequenziale
• Computer parallelo

A seconda dell'architettura dei computer, abbiamo due tipi di algoritmi:

• Sequential Algorithm - Un algoritmo in cui vengono eseguiti alcuni passaggi consecutivi di istruzioni in ordine cronologico per risolvere un problema.

• Parallel Algorithm- Il problema è suddiviso in sottoproblemi e vengono eseguiti in parallelo per ottenere singoli output. Successivamente, questi singoli output vengono combinati insieme per ottenere l'output finale desiderato.

Non è facile suddividere un grosso problema in sub-problems. I problemi secondari possono avere dipendenza dai dati tra di loro. Pertanto, i processori devono comunicare tra loro per risolvere il problema.

È stato riscontrato che il tempo necessario ai processori per comunicare tra loro è maggiore del tempo di elaborazione effettivo. Quindi, durante la progettazione di un algoritmo parallelo, è necessario considerare un corretto utilizzo della CPU per ottenere un algoritmo efficiente.

Per progettare correttamente un algoritmo, dobbiamo avere un'idea chiara delle basi model of computation in un computer parallelo.

Modello di calcolo

Sia i computer sequenziali che quelli paralleli operano su un insieme (flusso) di istruzioni chiamate algoritmi. Questo insieme di istruzioni (algoritmo) istruisce il computer su ciò che deve fare in ogni passaggio.

A seconda del flusso di istruzioni e del flusso di dati, i computer possono essere classificati in quattro categorie:

• Computer con flusso di istruzioni singolo, flusso di dati singolo (SISD)
• Computer con flusso di istruzioni singolo, flusso di dati multipli (SIMD)
• Computer con più istruzioni, flusso di dati singolo (MISD)
• Flusso di istruzioni multiple, computer MIMD (Multiple Data Stream)

Computer SISD

I computer SISD contengono one control unit, one processing unit, e one memory unit.

In questo tipo di computer, il processore riceve un singolo flusso di istruzioni dall'unità di controllo e opera su un singolo flusso di dati dall'unità di memoria. Durante il calcolo, ad ogni passo, il processore riceve un'istruzione dall'unità di controllo e opera su un singolo dato ricevuto dall'unità di memoria.

Computer SIMD

I computer SIMD contengono one control unit, multiple processing units, e shared memory or interconnection network.

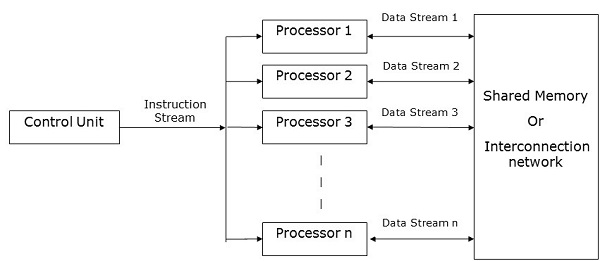
Qui, una singola unità di controllo invia istruzioni a tutte le unità di elaborazione. Durante il calcolo, ad ogni passo, tutti i processori ricevono un unico set di istruzioni dall'unità di controllo e operano su diversi set di dati dall'unità di memoria.

Ciascuna delle unità di elaborazione ha la propria unità di memoria locale per memorizzare sia i dati che le istruzioni. Nei computer SIMD, i processori devono comunicare tra loro. Questo viene fatto dashared memory o da interconnection network.

Mentre alcuni processori eseguono una serie di istruzioni, i restanti processori attendono la loro successiva serie di istruzioni. Le istruzioni dell'unità di controllo decidono quale processore saràactive (eseguire istruzioni) o inactive (attendere la prossima istruzione).

Computer MISD

Come suggerisce il nome, i computer MISD contengono multiple control units, multiple processing units, e one common memory unit.

Ogni processore ha la propria unità di controllo e condivide un'unità di memoria comune. Tutti i processori ricevono istruzioni singolarmente dalla propria unità di controllo e operano su un unico flusso di dati secondo le istruzioni che hanno ricevuto dalle rispettive unità di controllo. Questo processore funziona contemporaneamente.

Computer MIMD

I computer MIMD hanno multiple control units, multiple processing units, e a shared memory o interconnection network.

Ogni processore ha la propria unità di controllo, unità di memoria locale e unità aritmetica e logica. Ricevono diversi set di istruzioni dalle rispettive unità di controllo e operano su diversi set di dati.

Nota

• Un computer MIMD che condivide una memoria comune è noto come multiprocessors, mentre quelli che utilizzano una rete di interconnessione sono noti come multicomputers.

• In base alla distanza fisica dei processori, i multicomputer sono di due tipi:

  • Multicomputer - Quando tutti i processori sono molto vicini tra loro (es. Nella stessa stanza).

  • Distributed system - Quando tutti i processori sono lontani l'uno dall'altro (es- nelle diverse città)

L'analisi di un algoritmo ci aiuta a determinare se l'algoritmo è utile o meno. Generalmente, un algoritmo viene analizzato in base al suo tempo di esecuzione(Time Complexity) e la quantità di spazio (Space Complexity) richiede.

Poiché disponiamo di sofisticati dispositivi di memoria a un costo ragionevole, lo spazio di archiviazione non è più un problema. Quindi, alla complessità dello spazio non viene data molta importanza.

Gli algoritmi paralleli sono progettati per migliorare la velocità di calcolo di un computer. Per analizzare un algoritmo parallelo, normalmente consideriamo i seguenti parametri:

• Complessità temporale (tempo di esecuzione),
• Numero totale di processori utilizzati e
• Costo totale.

Complessità temporale

Il motivo principale alla base dello sviluppo di algoritmi paralleli era ridurre il tempo di calcolo di un algoritmo. Pertanto, la valutazione del tempo di esecuzione di un algoritmo è estremamente importante per analizzarne l'efficienza.

Il tempo di esecuzione viene misurato sulla base del tempo impiegato dall'algoritmo per risolvere un problema. Il tempo di esecuzione totale viene calcolato dal momento in cui l'algoritmo inizia l'esecuzione fino al momento in cui si ferma. Se tutti i processori non iniziano o terminano l'esecuzione nello stesso momento, il tempo di esecuzione totale dell'algoritmo è il momento in cui il primo processore ha iniziato la sua esecuzione fino al momento in cui l'ultimo processore interrompe la sua esecuzione.

La complessità temporale di un algoritmo può essere classificata in tre categorie:

• Worst-case complexity - Quando la quantità di tempo richiesta da un algoritmo per un dato input è maximum.

• Average-case complexity - Quando la quantità di tempo richiesta da un algoritmo per un dato input è average.

• Best-case complexity - Quando la quantità di tempo richiesta da un algoritmo per un dato input è minimum.

Analisi asintotica

La complessità o l'efficienza di un algoritmo è il numero di passaggi eseguiti dall'algoritmo per ottenere l'output desiderato. L'analisi asintotica viene eseguita per calcolare la complessità di un algoritmo nella sua analisi teorica. Nell'analisi asintotica, viene utilizzata una grande lunghezza di input per calcolare la funzione di complessità dell'algoritmo.

Note - Asymptoticè una condizione in cui una linea tende a incontrare una curva, ma non si intersecano. Qui la linea e la curva sono asintotiche tra loro.

La notazione asintotica è il modo più semplice per descrivere il tempo di esecuzione più veloce e più lento possibile per un algoritmo che utilizza limiti alti e limiti bassi sulla velocità. Per questo, usiamo le seguenti notazioni:

• Notazione O grande
• Notazione Omega
• Notazione Theta

Notazione O grande

In matematica, la notazione Big O viene utilizzata per rappresentare le caratteristiche asintotiche delle funzioni. Rappresenta il comportamento di una funzione per input di grandi dimensioni in un metodo semplice e accurato. È un metodo per rappresentare il limite superiore del tempo di esecuzione di un algoritmo. Rappresenta il tempo più lungo che l'algoritmo potrebbe impiegare per completare la sua esecuzione. La funzione -

f (n) = O (g (n))

se e solo se esistono costanti positive c e n₀ tale che f(n) ≤ c * g(n) per tutti n dove n ≥ n₀.

Notazione Omega

La notazione Omega è un metodo per rappresentare il limite inferiore del tempo di esecuzione di un algoritmo. La funzione -

f (n) = Ω (g (n))

se e solo se esistono costanti positive c e n₀ tale che f(n) ≥ c * g(n) per tutti n dove n ≥ n₀.

Notazione Theta

La notazione theta è un metodo per rappresentare sia il limite inferiore che il limite superiore del tempo di esecuzione di un algoritmo. La funzione -

f (n) = θ (g (n))

se e solo se esistono costanti positive c₁, c₂, e n₀ tale che c1 * g (n) ≤ f (n) ≤ c2 * g (n) per tutti n dove n ≥ n₀.

Accelerazione di un algoritmo

Le prestazioni di un algoritmo parallelo sono determinate calcolandone speedup. L'accelerazione è definita come il rapporto tra il tempo di esecuzione nel caso peggiore dell'algoritmo sequenziale più veloce noto per un particolare problema e il tempo di esecuzione nel caso peggiore dell'algoritmo parallelo.

Numero di processori utilizzati

Il numero di processori utilizzati è un fattore importante per analizzare l'efficienza di un algoritmo parallelo. Viene calcolato il costo per l'acquisto, la manutenzione e il funzionamento dei computer. Maggiore è il numero di processori utilizzati da un algoritmo per risolvere un problema, più costoso diventa il risultato ottenuto.

Costo totale

Il costo totale di un algoritmo parallelo è il prodotto della complessità temporale e del numero di processori utilizzati in quel particolare algoritmo.

Costo totale = complessità temporale × numero di processori utilizzati

quindi, il efficiency di un algoritmo parallelo è -

Il modello di un algoritmo parallelo viene sviluppato considerando una strategia per la divisione dei dati e il metodo di elaborazione e applicando una strategia adeguata per ridurre le interazioni. In questo capitolo, discuteremo i seguenti modelli di algoritmi paralleli:

• Modello parallelo dei dati
• Modello grafico attività
• Modello piscina da lavoro
• Modello master slave
• Produttore consumatore o modello di pipeline
• Modello ibrido

Dati paralleli

Nel modello parallelo di dati, le attività vengono assegnate ai processi e ciascuna attività esegue tipi simili di operazioni su dati diversi. Data parallelism è una conseguenza di singole operazioni che vengono applicate su più elementi di dati.

Il modello parallelo dei dati può essere applicato su spazi di indirizzi condivisi e paradigmi di passaggio di messaggi. Nel modello parallelo ai dati, le spese generali di interazione possono essere ridotte selezionando una località che preserva la decomposizione, utilizzando routine di interazione collettiva ottimizzate o sovrapponendo calcolo e interazione.

La caratteristica principale dei problemi del modello parallelo dei dati è che l'intensità del parallelismo dei dati aumenta con la dimensione del problema, il che a sua volta rende possibile utilizzare più processi per risolvere problemi più grandi.

Example - Moltiplicazione di matrici dense.

Modello grafico attività

Nel modello del grafico delle attività, il parallelismo è espresso da a task graph. Un grafico delle attività può essere banale o non banale. In questo modello, la correlazione tra i compiti viene utilizzata per promuovere la località o per ridurre al minimo i costi di interazione. Questo modello viene applicato per risolvere problemi in cui la quantità di dati associati alle attività è enorme rispetto al numero di calcoli ad essi associati. Le attività vengono assegnate per aiutare a migliorare il costo dello spostamento dei dati tra le attività.

Examples - Ordinamento rapido parallelo, fattorizzazione di matrici sparse e algoritmi paralleli derivati ​​tramite l'approccio divide et impera.

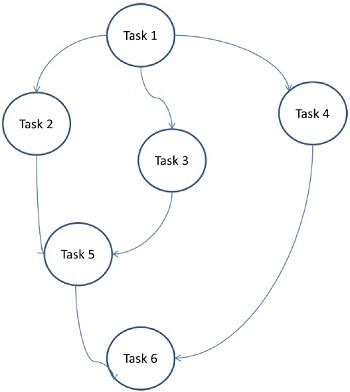
Qui, i problemi sono suddivisi in attività atomiche e implementati come un grafico. Ogni attività è un'unità di lavoro indipendente che ha dipendenze da una o più attività antecedenti. Dopo il completamento di un'attività, l'output di un'attività antecedente viene passato all'attività dipendente. Un'attività con attività antecedente avvia l'esecuzione solo quando l'intera attività antecedente è stata completata. L'output finale del grafico viene ricevuto al completamento dell'ultima attività dipendente (Attività 6 nella figura sopra).

Modello di piscina di lavoro

Nel modello del pool di lavoro, le attività vengono assegnate dinamicamente ai processi per il bilanciamento del carico. Pertanto, qualsiasi processo può potenzialmente eseguire qualsiasi attività. Questo modello viene utilizzato quando la quantità di dati associati alle attività è relativamente inferiore al calcolo associato alle attività.

Non vi è alcuna pre-assegnazione desiderata delle attività sui processi. L'assegnazione dei compiti è centralizzata o decentralizzata. I puntatori alle attività vengono salvati in un elenco condiviso fisicamente, in una coda di priorità o in una tabella hash o albero, oppure possono essere salvati in una struttura dati distribuita fisicamente.

L'attività può essere disponibile all'inizio o può essere generata dinamicamente. Se l'attività viene generata dinamicamente e viene eseguita un'assegnazione decentralizzata dell'attività, è necessario un algoritmo di rilevamento della terminazione in modo che tutti i processi possano effettivamente rilevare il completamento dell'intero programma e interrompere la ricerca di ulteriori attività.

Example - Ricerca ad albero parallelo

Modello Master-Slave

Nel modello master-slave, uno o più processi master generano l'attività e la allocano ai processi slave. I compiti possono essere assegnati in anticipo se:

• il master può stimare il volume delle attività, o
• un'assegnazione casuale può svolgere un lavoro soddisfacente di bilanciamento del carico, o
• agli schiavi vengono assegnati compiti più piccoli in momenti diversi.

Questo modello è generalmente ugualmente adatto a shared-address-space o message-passing paradigms, poiché l'interazione è naturalmente in due modi.

In alcuni casi, potrebbe essere necessario completare un'attività in fasi e l'attività in ciascuna fase deve essere completata prima di poter generare l'attività nelle fasi successive. Il modello master-slave può essere generalizzato ahierarchical o multi-level master-slave model in cui il master di livello superiore fornisce la gran parte dei compiti al master di secondo livello, che suddivide ulteriormente i compiti tra i propri schiavi e può svolgere una parte del compito stesso.

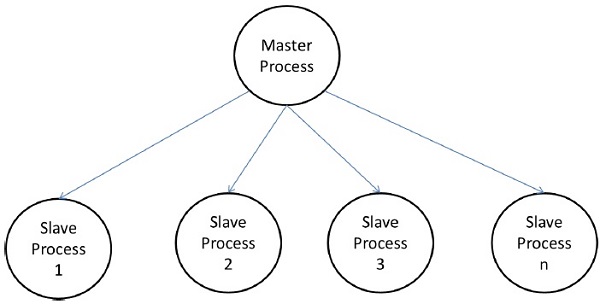
Precauzioni nell'utilizzo del modello master-slave

È necessario prestare attenzione per garantire che il master non diventi un punto di congestione. Può accadere se le attività sono troppo piccole o i lavoratori sono relativamente veloci.

Le attività dovrebbero essere selezionate in modo tale che il costo di esecuzione di un'attività domini il costo della comunicazione e il costo della sincronizzazione.

L'interazione asincrona può aiutare a sovrapporre l'interazione e il calcolo associato alla generazione di lavoro da parte del master.

Modello di pipeline

È anche conosciuto come producer-consumer model. Qui un insieme di dati viene trasmesso attraverso una serie di processi, ognuno dei quali esegue alcune attività su di esso. Qui, l'arrivo di nuovi dati genera l'esecuzione di una nuova attività da parte di un processo in coda. I processi potrebbero formare una coda sotto forma di matrici lineari o multidimensionali, alberi o grafici generali con o senza cicli.

Questo modello è una catena di produttori e consumatori. Ogni processo nella coda può essere considerato come consumatore di una sequenza di elementi di dati per il processo che lo precede nella coda e come produttore di dati per il processo che lo segue nella coda. La coda non deve essere una catena lineare; può essere un grafo diretto. La tecnica di minimizzazione dell'interazione più comune applicabile a questo modello è la sovrapposizione dell'interazione con il calcolo.

Example - Algoritmo di fattorizzazione LU parallela.

Modelli ibridi

Un modello di algoritmo ibrido è necessario quando può essere necessario più di un modello per risolvere un problema.

Un modello ibrido può essere composto da più modelli applicati gerarchicamente o da più modelli applicati sequenzialmente a diverse fasi di un algoritmo parallelo.

Example - Ordinamento rapido parallelo

Parallel Random Access Machines (PRAM)è un modello, che è considerato per la maggior parte degli algoritmi paralleli. Qui, più processori sono collegati a un singolo blocco di memoria. Un modello PRAM contiene:

• Un insieme di processori di tipo simile.

• Tutti i processori condividono un'unità di memoria comune. I processori possono comunicare tra di loro solo attraverso la memoria condivisa.

• Un'unità di accesso alla memoria (MAU) collega i processori con la singola memoria condivisa.

Qui, n numero di processori su cui è possibile eseguire operazioni indipendenti nnumero di dati in una particolare unità di tempo. Ciò può comportare l'accesso simultaneo alla stessa posizione di memoria da parte di processori diversi.

Per risolvere questo problema, i seguenti vincoli sono stati applicati al modello PRAM:

• Exclusive Read Exclusive Write (EREW) - Qui non è consentito a due processori di leggere o scrivere nella stessa posizione di memoria contemporaneamente.

• Exclusive Read Concurrent Write (ERCW) - Qui non è consentito a due processori di leggere dalla stessa posizione di memoria allo stesso tempo, ma possono scrivere nella stessa posizione di memoria allo stesso tempo.

• Concurrent Read Exclusive Write (CREW) - Qui tutti i processori possono leggere dalla stessa posizione di memoria allo stesso tempo, ma non sono autorizzati a scrivere nella stessa posizione di memoria allo stesso tempo.

• Concurrent Read Concurrent Write (CRCW) - Tutti i processori possono leggere o scrivere nella stessa posizione di memoria contemporaneamente.

Esistono molti metodi per implementare il modello PRAM, ma i più importanti sono:

• Modello di memoria condivisa
• Modello di passaggio del messaggio
• Modello parallelo dei dati

Modello di memoria condivisa

La memoria condivisa enfatizza control parallelism che su data parallelism. Nel modello di memoria condivisa, più processi vengono eseguiti su processori diversi in modo indipendente, ma condividono uno spazio di memoria comune. A causa di qualsiasi attività del processore, se c'è qualche cambiamento in una posizione di memoria, è visibile al resto dei processori.

Poiché più processori accedono alla stessa posizione di memoria, può accadere che in un determinato momento, più di un processore acceda alla stessa posizione di memoria. Supponiamo che uno stia leggendo quella posizione e l'altro stia scrivendo in quella posizione. Può creare confusione. Per evitare ciò, alcuni meccanismi di controllo, comelock / semaphore, è implementato per garantire l'esclusione reciproca.

La programmazione della memoria condivisa è stata implementata nel seguente:

• Thread libraries- La libreria di thread consente più thread di controllo che vengono eseguiti contemporaneamente nella stessa posizione di memoria. La libreria di thread fornisce un'interfaccia che supporta il multithreading tramite una libreria di subroutine. Contiene subroutine per

  • Creazione e distruzione di thread
  • Pianificazione dell'esecuzione del thread
  • passaggio di dati e messaggi tra i thread
  • salvataggio e ripristino dei contesti dei thread

Esempi di librerie di thread includono: thread SolarisTM per Solaris, thread POSIX come implementati in Linux, thread Win32 disponibili in Windows NT e Windows 2000 e thread JavaTM come parte del JavaTM Development Kit (JDK) standard.

• Distributed Shared Memory (DSM) Systems- I sistemi DSM creano un'astrazione della memoria condivisa su un'architettura debolmente accoppiata al fine di implementare la programmazione della memoria condivisa senza supporto hardware. Implementano librerie standard e utilizzano le funzionalità avanzate di gestione della memoria a livello utente presenti nei sistemi operativi moderni. Gli esempi includono Tread Marks System, Munin, IVY, Shasta, Brazos e Cashmere.

• Program Annotation Packages- Questo è implementato sulle architetture che hanno caratteristiche di accesso alla memoria uniformi. L'esempio più notevole di pacchetti di annotazioni di programmi è OpenMP. OpenMP implementa il parallelismo funzionale. Si concentra principalmente sulla parallelizzazione dei cicli.

Il concetto di memoria condivisa fornisce un controllo di basso livello del sistema di memoria condivisa, ma tende ad essere noioso ed errato. È più applicabile alla programmazione del sistema che alla programmazione dell'applicazione.

Meriti della programmazione con memoria condivisa

• Lo spazio degli indirizzi globale offre un approccio di programmazione intuitivo alla memoria.

• A causa della vicinanza della memoria alla CPU, la condivisione dei dati tra i processi è veloce e uniforme.

• Non è necessario specificare distintamente la comunicazione dei dati tra i processi.

• Il sovraccarico della comunicazione di processo è trascurabile.

• È molto facile da imparare.

Demeriti della programmazione della memoria condivisa

• Non è portatile.
• La gestione della località dei dati è molto difficile.

Modello di passaggio del messaggio

Il passaggio dei messaggi è l'approccio di programmazione parallela più comunemente utilizzato nei sistemi di memoria distribuita. Qui, il programmatore deve determinare il parallelismo. In questo modello, tutti i processori hanno una propria unità di memoria locale e scambiano dati attraverso una rete di comunicazione.

I processori utilizzano librerie di passaggio di messaggi per la comunicazione tra di loro. Insieme ai dati inviati, il messaggio contiene i seguenti componenti:

• L'indirizzo del processore da cui viene inviato il messaggio;

• Indirizzo iniziale della posizione di memoria dei dati nel processore mittente;

• Tipo di dati dei dati di invio;

• Dimensioni dei dati di invio;

• L'indirizzo del processore a cui viene inviato il messaggio;

• Indirizzo iniziale della posizione di memoria per i dati nel processore ricevente.

I processori possono comunicare tra loro tramite uno dei seguenti metodi:

• Comunicazione punto a punto
• Comunicazione collettiva
• Interfaccia di passaggio dei messaggi

Comunicazione punto a punto

La comunicazione punto a punto è la forma più semplice di trasmissione di messaggi. Qui, un messaggio può essere inviato dal processore mittente a un processore ricevente mediante una delle seguenti modalità di trasferimento:

• Synchronous mode - Il messaggio successivo viene inviato solo dopo aver ricevuto una conferma che il suo messaggio precedente è stato consegnato, per mantenere la sequenza del messaggio.

• Asynchronous mode - Per inviare il messaggio successivo, non è richiesta la ricezione della conferma di consegna del messaggio precedente.

Comunicazione collettiva

La comunicazione collettiva coinvolge più di due processori per il passaggio dei messaggi. Le seguenti modalità consentono comunicazioni collettive:

• Barrier - La modalità barriera è possibile se tutti i processori inclusi nelle comunicazioni eseguono un particolare bock (noto come barrier block) per il passaggio dei messaggi.

• Broadcast - La trasmissione è di due tipi:

  • One-to-all - Qui, un processore con una singola operazione invia lo stesso messaggio a tutti gli altri processori.

  • All-to-all - Qui, tutti i processori inviano un messaggio a tutti gli altri processori.

I messaggi trasmessi possono essere di tre tipi:

• Personalized - I messaggi univoci vengono inviati a tutti gli altri processori di destinazione.

• Non-personalized - Tutti i processori di destinazione ricevono lo stesso messaggio.

• Reduction - Nella trasmissione di riduzione, un processore del gruppo raccoglie tutti i messaggi da tutti gli altri processori del gruppo e li combina in un unico messaggio a cui possono accedere tutti gli altri processori del gruppo.

Meriti del passaggio del messaggio

• Fornisce un controllo di basso livello del parallelismo;
• È portatile;
• Meno soggetto a errori;
• Meno overhead nella sincronizzazione parallela e nella distribuzione dei dati.

Demeriti del passaggio di messaggi

• Rispetto al codice di memoria condivisa parallelo, il codice di passaggio dei messaggi generalmente richiede un sovraccarico software maggiore.

Librerie di passaggio di messaggi

Esistono molte librerie di passaggio di messaggi. Qui, discuteremo due delle librerie di passaggio di messaggi più utilizzate:

• Message Passing Interface (MPI)
• Macchina virtuale parallela (PVM)

Message Passing Interface (MPI)

È uno standard universale per fornire la comunicazione tra tutti i processi simultanei in un sistema di memoria distribuita. La maggior parte delle piattaforme di calcolo parallelo comunemente utilizzate fornisce almeno un'implementazione dell'interfaccia di passaggio dei messaggi. È stato implementato come raccolta di funzioni predefinite chiamatelibrary e possono essere richiamati da linguaggi come C, C ++, Fortran, ecc. Le MPI sono sia veloci che portatili rispetto alle altre librerie di passaggio di messaggi.

Merits of Message Passing Interface

• Funziona solo su architetture di memoria condivisa o architetture di memoria distribuita;

• Ogni processore ha le proprie variabili locali;

• Rispetto ai computer con memoria condivisa di grandi dimensioni, i computer con memoria distribuita sono meno costosi.

Demerits of Message Passing Interface

• Sono necessarie ulteriori modifiche alla programmazione per l'algoritmo parallelo;
• A volte è difficile eseguire il debug; e
• Non funziona bene nella rete di comunicazione tra i nodi.

Macchina virtuale parallela (PVM)

PVM è un sistema di trasmissione di messaggi portatile, progettato per connettere macchine host eterogenee separate per formare un'unica macchina virtuale. È una singola risorsa di calcolo parallelo gestibile. Grandi problemi computazionali come studi di superconduttività, simulazioni di dinamica molecolare e algoritmi di matrice possono essere risolti in modo più economico utilizzando la memoria e la potenza aggregata di molti computer. Gestisce tutto il routing dei messaggi, la conversione dei dati, la pianificazione delle attività nella rete di architetture di computer incompatibili.

Features of PVM

• Molto facile da installare e configurare;
• Più utenti possono utilizzare PVM contemporaneamente;
• Un utente può eseguire più applicazioni;
• È un piccolo pacchetto;
• Supporta C, C ++, Fortran;
• Per una data esecuzione di un programma PVM, gli utenti possono selezionare il gruppo di macchine;
• È un modello di trasmissione di messaggi,
• Calcolo basato sul processo;
• Supporta un'architettura eterogenea.

Programmazione parallela dei dati

L'obiettivo principale del modello di programmazione parallela dei dati è l'esecuzione simultanea di operazioni su un set di dati. Il set di dati è organizzato in una struttura come un array, un ipercubo, ecc. I processori eseguono operazioni collettivamente sulla stessa struttura di dati. Ogni attività viene eseguita su una partizione diversa della stessa struttura dati.

È restrittivo, poiché non tutti gli algoritmi possono essere specificati in termini di parallelismo dei dati. Questo è il motivo per cui il parallelismo dei dati non è universale.

I linguaggi paralleli dei dati aiutano a specificare la scomposizione dei dati e la mappatura ai processori. Include anche istruzioni di distribuzione dei dati che consentono al programmatore di avere il controllo sui dati, ad esempio quali dati andranno su quale processore, per ridurre la quantità di comunicazione all'interno dei processori.

Per applicare correttamente qualsiasi algoritmo, è molto importante selezionare una struttura dati adeguata. È perché una particolare operazione eseguita su una struttura dati può richiedere più tempo rispetto alla stessa operazione eseguita su un'altra struttura dati.

Example- Per accedere all'i- ^esimo elemento di un insieme utilizzando un array, potrebbe essere necessario un tempo costante ma utilizzando un elenco collegato, il tempo necessario per eseguire la stessa operazione potrebbe diventare un polinomio.

Pertanto, la selezione di una struttura dati deve essere fatta considerando l'architettura e il tipo di operazioni da eseguire.

Le seguenti strutture di dati sono comunemente utilizzate nella programmazione parallela:

• Lista collegata
• Arrays
• Rete Hypercube

Lista collegata

Un elenco collegato è una struttura di dati con zero o più nodi collegati da puntatori. I nodi possono o meno occupare posizioni di memoria consecutive. Ogni nodo ha due o tre parti: unadata part che memorizza i dati e gli altri due lo sono link fieldsche memorizzano l'indirizzo del nodo precedente o successivo. L'indirizzo del primo nodo è memorizzato in un puntatore esterno chiamatohead. L'ultimo nodo, noto cometail, generalmente non contiene alcun indirizzo.

Esistono tre tipi di elenchi collegati:

• Elenco collegato singolarmente
• Elenco doppiamente collegato
• Elenco collegato circolare

Elenco collegato singolarmente

Un nodo di un elenco collegato singolarmente contiene i dati e l'indirizzo del nodo successivo. Un puntatore esterno chiamatohead memorizza l'indirizzo del primo nodo.

Elenco doppiamente collegato

Un nodo di una lista doppiamente collegata contiene i dati e l'indirizzo sia del nodo precedente che di quello successivo. Un puntatore esterno chiamatohead memorizza l'indirizzo del primo nodo e il puntatore esterno chiamato tail memorizza l'indirizzo dell'ultimo nodo.

Elenco collegato circolare

Un elenco collegato circolare è molto simile all'elenco collegato singolarmente tranne per il fatto che l'ultimo nodo ha salvato l'indirizzo del primo nodo.

Array

Un array è una struttura di dati in cui possiamo memorizzare tipi di dati simili. Può essere unidimensionale o multidimensionale. Gli array possono essere creati staticamente o dinamicamente.

• In statically declared arrays, dimensione e dimensione degli array sono note al momento della compilazione.

• In dynamically declared arrays, dimensione e dimensione della matrice sono note in fase di esecuzione.

Per la programmazione della memoria condivisa, gli array possono essere utilizzati come una memoria comune e per la programmazione parallela dei dati, possono essere utilizzati partizionando in sotto-array.

Rete Hypercube

L'architettura Hypercube è utile per quegli algoritmi paralleli in cui ogni attività deve comunicare con altre attività. La topologia dell'ipercubo può facilmente incorporare altre topologie come anello e mesh. È anche noto come n-cubi, dovenè il numero di dimensioni. Un ipercubo può essere costruito ricorsivamente.

Selezionare una tecnica di progettazione adeguata per un algoritmo parallelo è il compito più difficile e importante. La maggior parte dei problemi di programmazione parallela può avere più di una soluzione. In questo capitolo, discuteremo le seguenti tecniche di progettazione per algoritmi paralleli:

• Dividere e conquistare
• Metodo goloso
• Programmazione dinamica
• Backtracking
• Branch & Bound
• Programmazione lineare

Metodo Dividi e conquista

Nell'approccio divide et impera, il problema è suddiviso in diversi piccoli sottoproblemi. Quindi i sottoproblemi vengono risolti ricorsivamente e combinati per ottenere la soluzione del problema originale.

L'approccio divide et impera prevede i seguenti passaggi ad ogni livello:

• Divide - Il problema originale è suddiviso in sottoproblemi.

• Conquer - I problemi secondari vengono risolti in modo ricorsivo.

• Combine - Le soluzioni dei sottoproblemi vengono combinate insieme per ottenere la soluzione del problema originale.

L'approccio divide et impera viene applicato nei seguenti algoritmi:

• Ricerca binaria
• Ordinamento veloce
• Unisci ordinamento
• Moltiplicazione intera
• Inversione della matrice
• Moltiplicazione di matrici

Metodo goloso

Nell'algoritmo avido di soluzione di ottimizzazione, la soluzione migliore viene scelta in qualsiasi momento. Un algoritmo avido è molto facile da applicare a problemi complessi. Decide quale passaggio fornirà la soluzione più accurata nel passaggio successivo.

Questo algoritmo è chiamato greedyperché quando viene fornita la soluzione ottimale per l'istanza più piccola, l'algoritmo non considera il programma totale nel suo complesso. Una volta presa in considerazione una soluzione, l'algoritmo greedy non considera mai più la stessa soluzione.

Un algoritmo avido funziona in modo ricorsivo creando un gruppo di oggetti dalle parti componenti più piccole possibili. La ricorsione è una procedura per risolvere un problema in cui la soluzione a un problema specifico dipende dalla soluzione dell'istanza più piccola di quel problema.

Programmazione dinamica

La programmazione dinamica è una tecnica di ottimizzazione, che divide il problema in sotto-problemi più piccoli e dopo aver risolto ogni sotto-problema, la programmazione dinamica combina tutte le soluzioni per ottenere la soluzione definitiva. A differenza del metodo divide et impera, la programmazione dinamica riutilizza molte volte la soluzione ai sottoproblemi.

L'algoritmo ricorsivo per la serie di Fibonacci è un esempio di programmazione dinamica.

Algoritmo di backtracking

Il backtracking è una tecnica di ottimizzazione per risolvere problemi combinatori. Viene applicato sia a problemi programmatici che di vita reale. Il problema delle otto regina, il puzzle di Sudoku e il passaggio in un labirinto sono esempi popolari in cui viene utilizzato l'algoritmo di backtracking.

Nel backtracking, partiamo da una possibile soluzione, che soddisfi tutte le condizioni richieste. Quindi passiamo al livello successivo e se quel livello non produce una soluzione soddisfacente, torniamo indietro di un livello e iniziamo con una nuova opzione.

Branch and Bound

Un algoritmo branch and bound è una tecnica di ottimizzazione per ottenere una soluzione ottimale al problema. Cerca la migliore soluzione per un dato problema nell'intero spazio della soluzione. I limiti nella funzione da ottimizzare vengono uniti al valore della migliore soluzione più recente. Consente all'algoritmo di trovare completamente parti dello spazio della soluzione.

Lo scopo di una ricerca branch and bound è mantenere il percorso più economico verso un target. Una volta trovata una soluzione, può continuare a migliorare la soluzione. La ricerca branch and bound viene implementata nella ricerca delimitata in profondità e nella ricerca in profondità.

Programmazione lineare

La programmazione lineare descrive un'ampia classe di lavori di ottimizzazione in cui sia il criterio di ottimizzazione che i vincoli sono funzioni lineari. È una tecnica per ottenere il miglior risultato come il massimo profitto, il percorso più breve o il costo più basso.

In questa programmazione, abbiamo un insieme di variabili a cui dobbiamo assegnare valori assoluti per soddisfare un insieme di equazioni lineari e per massimizzare o minimizzare una data funzione obiettivo lineare.

Una matrice è un insieme di dati numerici e non numerici disposti in un numero fisso di righe e colonne. La moltiplicazione di matrici è un importante progetto di moltiplicazione nel calcolo parallelo. Qui discuteremo l'implementazione della moltiplicazione di matrici su varie reti di comunicazione come mesh e hypercube. Mesh e hypercube hanno una connettività di rete più elevata, quindi consentono un algoritmo più veloce rispetto ad altre reti come la rete ad anello.

Rete Mesh

Una topologia in cui un insieme di nodi forma una griglia p-dimensionale è chiamata topologia mesh. Qui, tutti i bordi sono paralleli all'asse della griglia e tutti i nodi adiacenti possono comunicare tra loro.

Numero totale di nodi = (numero di nodi nella riga) × (numero di nodi nella colonna)

Una rete mesh può essere valutata utilizzando i seguenti fattori:

• Diameter
• Larghezza di bisezione

Diameter - In una rete mesh, la più lunga distancetra due nodi è il suo diametro. Una rete mesh p-dimensionale aventekP nodi ha un diametro di p(k–1).

Bisection width - La larghezza di bisezione è il numero minimo di bordi che devono essere rimossi da una rete per dividere la rete a maglie in due metà.

Moltiplicazione di matrici utilizzando la rete mesh

Abbiamo considerato un modello SIMD di rete mesh 2D con connessioni avvolgenti. Progetteremo un algoritmo per moltiplicare due n × n array utilizzando n ² processori in un determinato periodo di tempo.

Le matrici A e B hanno elementi a _ij e b _ij rispettivamente. L'elemento di elaborazione PE _ij rappresenta a _ij eb _ij . Disporre le matrici A e B in modo tale che ogni processore abbia una coppia di elementi da moltiplicare. Gli elementi della matrice A si sposteranno nella direzione sinistra e gli elementi della matrice B si muoveranno verso l'alto. Questi cambiamenti nella posizione degli elementi nella matrice A e B presentano ad ogni elemento di elaborazione, PE, una nuova coppia di valori da moltiplicare.

Fasi dell'algoritmo

• Sfalsa due matrici.
• Calcola tutti i prodotti, a _ik × b _kj
• Calcola le somme al termine del passaggio 2.

Algoritmo

Procedure MatrixMulti

Begin
   for k = 1 to n-1
	
   for all Pij; where i and j ranges from 1 to n
      ifi is greater than k then
         rotate a in left direction
      end if
		
   if j is greater than k then
      rotate b in the upward direction
   end if
	
   for all Pij ; where i and j lies between 1 and n
      compute the product of a and b and store it in c
   for k= 1 to n-1 step 1
   for all Pi;j where i and j ranges from 1 to n
      rotate a in left direction
      rotate b in the upward direction
      c=c+aXb
End

Rete Hypercube

Un ipercubo è un costrutto n-dimensionale in cui i bordi sono perpendicolari tra loro e hanno la stessa lunghezza. Un ipercubo n-dimensionale è anche noto come cubo n o cubo n-dimensionale.

Caratteristiche di Hypercube con 2 ^k nodi

• Diametro = k
• Larghezza di bisezione = 2 ^{k – 1}
• Numero di spigoli = k

Moltiplicazione di matrici utilizzando Hypercube Network

Specifiche generali delle reti Hypercube -

• Permettere N = 2^messere il numero totale di processori. Siano i processori P _0, P ₁ … ..P _N-1 .

• Siano i e i ^b due numeri interi, 0 <i, i ^b <N-1 e la sua rappresentazione binaria differisce solo nella posizione b, 0 <b <k – 1.

• Consideriamo due matrici n × n, matrice A e matrice B.

• Step 1- Gli elementi della matrice A e della matrice B sono assegnati agli n ³ processori in modo tale che il processore in posizione i, j, k avrà a _ji eb _ik .

• Step 2 - Tutto il processore in posizione (i, j, k) calcola il prodotto

  C (i, j, k) = A (i, j, k) × B (i, j, k)

• Step 3 - La somma C (0, j, k) = ΣC (i, j, k) per 0 ≤ i ≤ n-1, dove 0 ≤ j, k <n – 1.

Matrice a blocchi

Block Matrix o matrice partizionata è una matrice in cui ogni elemento stesso rappresenta una matrice individuale. Queste singole sezioni sono note come fileblock o sub-matrix.

Esempio

Nella Figura (a), X è una matrice a blocchi in cui A, B, C, D sono matrici stesse. La figura (f) mostra la matrice totale.

Moltiplicazione di matrici a blocchi

Quando due matrici a blocchi sono matrici quadrate, vengono moltiplicate nello stesso modo in cui eseguiamo la moltiplicazione di matrici semplice. Per esempio,

L'ordinamento è un processo di disposizione degli elementi in un gruppo in un ordine particolare, cioè, ordine crescente, ordine decrescente, ordine alfabetico, ecc. Qui discuteremo quanto segue:

• Ordinamento enumerazione
• Ordinamento di trasposizione pari-dispari
• Ordinamento unione parallela
• Ordinamento iper rapido

L'ordinamento di un elenco di elementi è un'operazione molto comune. Un algoritmo di ordinamento sequenziale potrebbe non essere abbastanza efficiente quando dobbiamo ordinare un enorme volume di dati. Pertanto, gli algoritmi paralleli vengono utilizzati nell'ordinamento.

Ordinamento enumerazione

L'ordinamento per enumerazione è un metodo per disporre tutti gli elementi in un elenco trovando la posizione finale di ogni elemento in un elenco ordinato. Viene fatto confrontando ogni elemento con tutti gli altri elementi e trovando il numero di elementi di valore inferiore.

Pertanto, per due elementi qualsiasi, a _i ea _j uno qualsiasi dei seguenti casi deve essere vero:

• a _i <a _j
• a _i > a _j
• a _i = a _j

Algoritmo

procedure ENUM_SORTING (n)

begin
   for each process P1,j do
      C[j] := 0;
		
   for each process Pi, j do
	
      if (A[i] < A[j]) or A[i] = A[j] and i < j) then
         C[j] := 1;
      else
         C[j] := 0;
			
   for each process P1, j do
      A[C[j]] := A[j];
		
end ENUM_SORTING

Ordinamento di trasposizione pari-dispari

L'ordinamento con trasposizione pari-dispari si basa sulla tecnica Bubble Sort. Confronta due numeri adiacenti e li scambia, se il primo numero è maggiore del secondo numero per ottenere un elenco in ordine crescente. Il caso opposto si applica a una serie in ordine decrescente. L'ordinamento della trasposizione pari-dispari opera in due fasi:odd phase e even phase. In entrambe le fasi, i processi scambiano numeri con il numero adiacente a destra.

Algoritmo

procedure ODD-EVEN_PAR (n) 

begin 
   id := process's label 
	
   for i := 1 to n do 
   begin 
	
      if i is odd and id is odd then 
         compare-exchange_min(id + 1); 
      else 
         compare-exchange_max(id - 1);
			
      if i is even and id is even then 
         compare-exchange_min(id + 1); 
      else 
         compare-exchange_max(id - 1);
			
   end for
	
end ODD-EVEN_PAR

Ordinamento unione parallela

Unisci prima l'ordinamento divide l'elenco non ordinato in sotto-elenchi più piccoli possibile, lo confronta con l'elenco adiacente e lo unisce in un ordine ordinato. Implementa molto bene il parallelismo seguendo l'algoritmo divide et impera.

Algoritmo

procedureparallelmergesort(id, n, data, newdata)

begin
   data = sequentialmergesort(data)
	
      for dim = 1 to n
         data = parallelmerge(id, dim, data)
      endfor
		
   newdata = data
end

Ordinamento iper rapido

L'ordinamento rapido iper è un'implementazione dell'ordinamento rapido su hypercube. I suoi passaggi sono i seguenti:

• Dividi l'elenco non ordinato tra ogni nodo.
• Ordina ogni nodo localmente.
• Dal nodo 0, trasmetti il ​​valore mediano.
• Dividi ogni elenco a livello locale, quindi scambia le due metà nella dimensione più alta.
• Ripetere i passaggi 3 e 4 in parallelo finché la dimensione non raggiunge 0.

Algoritmo

procedure HYPERQUICKSORT (B, n)
begin

   id := process’s label;
	
   for i := 1 to d do
      begin
      x := pivot;
      partition B into B1 and B2 such that B1 ≤ x < B2;
      if ith bit is 0 then
		
      begin
         send B2 to the process along the ith communication link;
         C := subsequence received along the ith communication link;
         B := B1 U C;
      endif
      
      else
         send B1 to the process along the ith communication link;
         C := subsequence received along the ith communication link;
         B := B2 U C;
         end else
      end for
		
   sort B using sequential quicksort;
	
end HYPERQUICKSORT

La ricerca è una delle operazioni fondamentali nell'informatica. Viene utilizzato in tutte le applicazioni in cui è necessario verificare se un elemento è nell'elenco fornito o meno. In questo capitolo, discuteremo i seguenti algoritmi di ricerca:

• Dividere e conquistare
• Ricerca in profondità
• Ricerca in ampiezza
• Migliore prima ricerca

Dividere e conquistare

Nell'approccio divide et impera, il problema è suddiviso in diversi piccoli problemi secondari. Quindi i sottoproblemi vengono risolti ricorsivamente e combinati per ottenere la soluzione del problema originale.

L'approccio divide et impera prevede i seguenti passaggi ad ogni livello:

• Divide - Il problema originale è suddiviso in sottoproblemi.

• Conquer - I problemi secondari vengono risolti in modo ricorsivo.

• Combine - Le soluzioni dei sottoproblemi vengono combinate per ottenere la soluzione del problema originale.

La ricerca binaria è un esempio di algoritmo divide et impera.

Pseudocodice

Binarysearch(a, b, low, high)

if low < high then
   return NOT FOUND
else
   mid ← (low+high) / 2
   if b = key(mid) then
      return key(mid)
   else if b < key(mid) then
      return BinarySearch(a, b, low, mid−1)
   else
   
      return BinarySearch(a, b, mid+1, high)

Ricerca in profondità

Depth-First Search (o DFS) è un algoritmo per la ricerca in un albero o in una struttura di dati del grafico non orientata. In questo caso, il concetto è di iniziare dal nodo di partenza noto comeroote traversa il più possibile nello stesso ramo. Se otteniamo un nodo senza nodo successore, torniamo e continuiamo con il vertice, che deve ancora essere visitato.

Fasi della ricerca in profondità

• Considera un nodo (root) che non è stato visitato in precedenza e contrassegnalo come visitato.

• Visita il primo nodo successore adiacente e contrassegnalo come visitato.

• Se tutti i nodi successori del nodo considerato sono già visitati o non ha più nodi successori, torna al suo nodo padre.

Pseudocodice

Permettere v essere il vertice in cui inizia la ricerca in Graph G.

DFS(G,v)

   Stack S := {};
	
   for each vertex u, set visited[u] := false;
   push S, v;
   while (S is not empty) do
     u := pop S;
	  
      if (not visited[u]) then
         visited[u] := true;
         for each unvisited neighbour w of u
            push S, w;
      end if
		
   end while
   
END DFS()

Ricerca in ampiezza

Breadth-First Search (o BFS) è un algoritmo per la ricerca in un albero o in una struttura di dati del grafo non orientata. Qui, iniziamo con un nodo e poi visitiamo tutti i nodi adiacenti nello stesso livello e poi ci spostiamo al nodo successore adiacente nel livello successivo. Questo è anche noto comelevel-by-level search.

Passi della ricerca in larghezza

• Inizia con il nodo radice, contrassegnalo come visitato.
• Poiché il nodo radice non ha alcun nodo allo stesso livello, passare al livello successivo.
• Visita tutti i nodi adiacenti e contrassegnali come visitati.
• Vai al livello successivo e visita tutti i nodi adiacenti non visitati.
• Continua questo processo fino a quando tutti i nodi non sono stati visitati.

Pseudocodice

Permettere v essere il vertice in cui inizia la ricerca in Graph G.

BFS(G,v)

   Queue Q := {};
	
   for each vertex u, set visited[u] := false;
   insert Q, v;
   while (Q is not empty) do
      u := delete Q;
		
      if (not visited[u]) then
         visited[u] := true;
         for each unvisited neighbor w of u
            insert Q, w;
      end if
		
   end while
   
END BFS()

Migliore prima ricerca

Best-First Search è un algoritmo che attraversa un grafico per raggiungere un obiettivo nel percorso più breve possibile. A differenza di BFS e DFS, Best-First Search segue una funzione di valutazione per determinare quale nodo è il più appropriato da attraversare successivamente.

Passaggi della ricerca migliore

• Inizia con il nodo radice, contrassegnalo come visitato.
• Trova il successivo nodo appropriato e contrassegnalo come visitato.
• Vai al livello successivo e trova il nodo appropriato e contrassegnalo come visitato.
• Continua questo processo fino a raggiungere l'obiettivo.

Pseudocodice

BFS( m )

   Insert( m.StartNode )
   Until PriorityQueue is empty
      c ← PriorityQueue.DeleteMin
      If c is the goal
      Exit
   Else
   
      Foreach neighbor n of c
         If n "Unvisited"
            Mark n "Visited"
            Insert( n )
      Mark c "Examined"
      
End procedure

Un grafico è una notazione astratta utilizzata per rappresentare la connessione tra coppie di oggetti. Un grafico è composto da:

• Vertices- Gli oggetti interconnessi in un grafo sono chiamati vertici. I vertici sono noti anche comenodes.

• Edges - I bordi sono i collegamenti che collegano i vertici.

Esistono due tipi di grafici:

• Directed graph - In un grafo orientato, gli archi hanno una direzione, cioè gli archi vanno da un vertice all'altro.

• Undirected graph - In un grafico non orientato, i bordi non hanno direzione.

Colorazione del grafico

La colorazione del grafo è un metodo per assegnare i colori ai vertici di un grafo in modo che non ci siano due vertici adiacenti dello stesso colore. Alcuni problemi di colorazione dei grafici sono:

• Vertex coloring - Un modo per colorare i vertici di un grafo in modo che non ci siano due vertici adiacenti che condividano lo stesso colore.

• Edge Coloring - È il metodo per assegnare un colore a ciascun bordo in modo che non ci siano due bordi adiacenti dello stesso colore.

• Face coloring - Assegna un colore a ciascuna faccia o regione di un grafico planare in modo che due facce che condividono un contorno comune non abbiano lo stesso colore.

Numero cromatico

Il numero cromatico è il numero minimo di colori richiesti per colorare un grafico. Ad esempio, il numero cromatico del grafico seguente è 3.

Il concetto di colorazione dei grafici viene applicato nella preparazione degli orari, nell'assegnazione delle radiofrequenze mobili, nel Suduku, nell'assegnazione dei registri e nella colorazione delle mappe.

Passaggi per la colorazione del grafico

• Imposta il valore iniziale di ogni processore nella matrice n-dimensionale su 1.

• Ora per assegnare un colore particolare a un vertice, determinare se quel colore è già assegnato ai vertici adiacenti o meno.

• Se un processore rileva lo stesso colore nei vertici adiacenti, imposta il suo valore nell'array a 0.

• Dopo aver eseguito n ² confronti, se un elemento dell'array è 1, allora è una colorazione valida.

Pseudocodice per la colorazione dei grafici

begin

   create the processors P(i0,i1,...in-1) where 0_iv < m, 0 _ v < n
   status[i0,..in-1] = 1
	
   for j varies from 0 to n-1 do
      begin
		
         for k varies from 0 to n-1 do
         begin
            if aj,k=1 and ij=ikthen
            status[i0,..in-1] =0
         end
			
      end
      ok = ΣStatus
		
   if ok > 0, then display valid coloring exists
   else
      display invalid coloring
      
end

Albero di copertura minimo

Uno spanning tree la cui somma del peso (o lunghezza) di tutti i suoi bordi è inferiore a tutti gli altri possibili spanning tree del grafo G è noto come minimal spanning tree o minimum cost spanningalbero. La figura seguente mostra un grafico connesso ponderato.

Alcuni possibili spanning tree del grafico sopra sono mostrati di seguito:

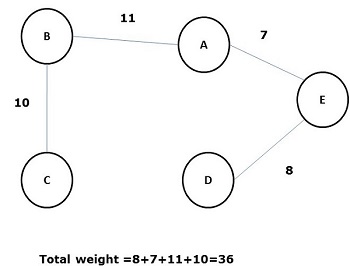
Tra tutti gli alberi di copertura di cui sopra, la figura (d) è l'albero di copertura minimo. Il concetto di albero di copertura del costo minimo viene applicato nel problema dei venditori ambulanti, nella progettazione di circuiti elettronici, nella progettazione di reti efficienti e nella progettazione di algoritmi di instradamento efficienti.

Per implementare l'albero di copertura del costo minimo, vengono utilizzati i due metodi seguenti:

• Algoritmo di Prim
• Algoritmo di Kruskal

Algoritmo di Prim

L'algoritmo di Prim è un algoritmo avido, che ci aiuta a trovare lo spanning tree minimo per un grafo non orientato ponderato. Seleziona prima un vertice e trova un bordo con il peso minore incidente su quel vertice.

Fasi dell'algoritmo di Prim

• Selezionare un vertice qualsiasi, ad esempio v ₁ del grafico G.

• Selezionare un arco, diciamo e ₁ di G tale che e ₁ = v ₁ v ₂ e v ₁ ≠ v ₂ ed e ₁ abbia un peso minimo tra gli archi incidenti su v ₁ nel grafico G.

• Ora, seguendo il passaggio 2, seleziona l'incidente del bordo ponderato minimo su v ₂ .

• Continuare finché non sono stati scelti n – 1 bordi. Quin è il numero di vertici.

Lo spanning tree minimo è -

Algoritmo di Kruskal

L'algoritmo di Kruskal è un algoritmo avido, che ci aiuta a trovare l'albero di copertura minimo per un grafo ponderato connesso, aggiungendo archi di costo crescenti ad ogni passaggio. È un algoritmo di albero di copertura minimo che trova un bordo del minor peso possibile che collega due alberi qualsiasi nella foresta.

Fasi dell'algoritmo di Kruskal

• Seleziona un bordo di peso minimo; diciamo e ₁ del grafico G ed e ₁ non è un ciclo.

• Selezionare il successivo bordo ponderato minimo collegato a e ₁ .

• Continuare finché non sono stati scelti n – 1 bordi. Quin è il numero di vertici.

Lo spanning tree minimo del grafico sopra è -

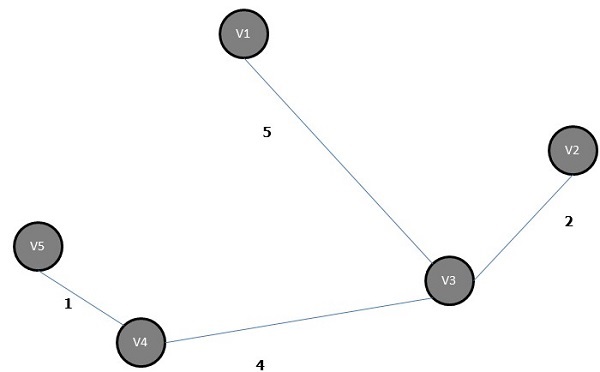
Algoritmo del percorso più breve

L'algoritmo del percorso più breve è un metodo per trovare il percorso meno costoso dal nodo di origine (S) al nodo di destinazione (D). Qui discuteremo l'algoritmo di Moore, noto anche come Breadth First Search Algorithm.

Algoritmo di Moore

• Etichetta il vertice di origine, S e etichettalo i e impostare i=0.

• Trova tutti i vertici senza etichetta adiacenti al vertice etichettato i. Se nessun vertice è connesso al vertice, S, allora il vertice, D, non è connesso a S. Se ci sono vertici collegati a S, etichettalii+1.

• Se D è etichettato, vai al passaggio 4, altrimenti vai al passaggio 2 per aumentare i = i + 1.

• Fermarsi dopo aver trovato la lunghezza del percorso più breve.