Fisica - Gravitazione
introduzione
Tutti i corpi celesti quelli trovati nell'universo si attraggono e la forza di attrazione tra questi corpi è chiamata come il gravitational force.

Legge universale di gravitazione
Ogni oggetto nell'universo ha la proprietà di attrarre ogni altro oggetto con una forza direttamente proporzionale al prodotto delle loro masse e inversamente proporzionale al quadrato della distanza tra di loro (vedi immagine sotto riportata).
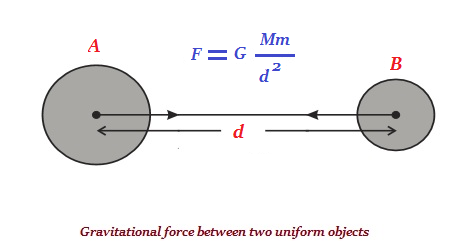
F = forza di attrazione tra due oggetti 'A' e 'B'
M = massa di 'A'
m = massa di 'B'
d2 = il quadrato della distanza tra "A" e "B"
G = è la costante di proporzionalità ed è nota come costante di gravitazione universale.
L'unità SI di G è N m2 kg–2. Si ottiene sostituendo le unità di forza, distanza e massa (come indicato nella seguente equazione -
$$ G = \ frac {Fd ^ 2} {M \ times m} $$
Henry Cavendish aveva calcolato il valore di ‘G’ come 6.673 × 10–11 N m2 kg–2.
Henry Cavendish aveva usato un equilibrio sensibile per trovare il valore di "G."
Significato della legge universale di gravitazione
Di seguito è riportato il significato saliente della Legge Universale di Gravitazione:
Spiega la forza che lega tutti gli oggetti (compresi gli esseri umani) alla terra
Descrive il movimento della luna intorno alla terra
Spiega il movimento dei pianeti attorno al Sole
Chiarisce le maree dovute alla luna e al sole
Caduta libera
Ogni volta che un oggetto cade verso la terra, comporta un'accelerazione; questa accelerazione è prodotta a causa della forza gravitazionale terrestre.

L'accelerazione, prodotta a causa della forza gravitazionale terrestre, è nota come accelerazione dovuta alla forza gravitazionale terrestre (o accelerazione dovuta alla gravità).
L'accelerazione prodotta a causa della forza gravitazionale è indicata con g.
Man mano che il raggio della terra aumenta verso l'equatore (dai poli) il valore di ‘g’ diventa maggiore ai poli che all'equatore.
Il valore di g
Il valore di g è calcolato come -
$$ g = G \ frac {M} {R ^ 2} $$
G = costante gravitazionale universale, che è = 6.7 × 10–11 N m2 kg-2
M = massa della terra, che è = 6 × 1024 kg
R = raggio della terra, che è = 6.4 × 106 m
So,
$$ g = \ frac {6.7 \: \ times 10 ^ {- 11} \: Nm ^ 2 \: kg ^ {- 2} \: \ times \: 6 \: \ times 10 ^ {24} \: kg } {(6.4 \: \ times 10 ^ 6 \: m) ^ 2} $$
$ = 9,8 \: m \: s ^ {- 2} $
Quindi, il valore dell'accelerazione dovuta alla gravità terrestre (g) è 9,8 ms -2 .