Scikit Learn - Guida rapida
In questo capitolo capiremo cos'è Scikit-Learn o Sklearn, l'origine di Scikit-Learn e alcuni altri argomenti correlati come comunità e collaboratori responsabili dello sviluppo e della manutenzione di Scikit-Learn, i suoi prerequisiti, l'installazione e le sue caratteristiche.
Cos'è Scikit-Learn (Sklearn)
Scikit-learn (Sklearn) è la libreria più utile e robusta per l'apprendimento automatico in Python. Fornisce una selezione di strumenti efficienti per l'apprendimento automatico e la modellazione statistica tra cui classificazione, regressione, clustering e riduzione della dimensionalità tramite un'interfaccia di coerenza in Python. Questa libreria, che è in gran parte scritta in Python, è costruita suNumPy, SciPy e Matplotlib.
Origine di Scikit-Learn
In origine si chiamava scikits.learn ed è stato inizialmente sviluppato da David Cournapeau come progetto Google Summer of Code nel 2007. Successivamente, nel 2010, Fabian Pedregosa, Gael Varoquaux, Alexandre Gramfort e Vincent Michel, del FIRCA (Istituto francese di ricerca in informatica e automazione), hanno questo progetto a un altro livello e ha reso la prima versione pubblica (v0.1 beta) il 1 ° febbraio 2010.
Diamo un'occhiata alla sua cronologia delle versioni:
Maggio 2019: scikit-learn 0.21.0
Marzo 2019: scikit-learn 0.20.3
Dicembre 2018: scikit-learn 0.20.2
Novembre 2018: scikit-learn 0.20.1
Settembre 2018: scikit-learn 0.20.0
Luglio 2018: scikit-learn 0.19.2
Luglio 2017: scikit-learn 0.19.0
Settembre 2016. scikit-learn 0.18.0
Novembre 2015. scikit-learn 0.17.0
Marzo 2015. scikit-learn 0.16.0
Luglio 2014. scikit-learn 0.15.0
Agosto 2013. scikit-learn 0.14
Comunità e collaboratori
Scikit-learn è uno sforzo della comunità e chiunque può contribuirvi. Questo progetto è ospitato suhttps://github.com/scikit-learn/scikit-learn. Le persone che seguono sono attualmente i principali contributori allo sviluppo e alla manutenzione di Sklearn -
Joris Van den Bossche (Data Scientist)
Thomas J Fan (Sviluppatore software)
Alexandre Gramfort (ricercatore in machine learning)
Olivier Grisel (esperto di machine learning)
Nicolas Hug (ricercatore associato)
Andreas Mueller (scienziato dell'apprendimento automatico)
Hanmin Qin (ingegnere del software)
Adrin Jalali (Sviluppatore Open Source)
Nelle Varoquaux (Data Science Researcher)
Roman Yurchak (Data Scientist)
Diverse organizzazioni come Booking.com, JP Morgan, Evernote, Inria, AWeber, Spotify e molte altre stanno utilizzando Sklearn.
Prerequisiti
Prima di iniziare a utilizzare l'ultima versione di scikit-learn, è necessario quanto segue:
Python (> = 3.5)
NumPy (> = 1.11.0)
Scipy (> = 0,17,0) li
Joblib (> = 0,11)
Matplotlib (> = 1.5.1) è richiesto per le funzionalità di plottaggio di Sklearn.
Pandas (> = 0.18.0) è richiesto per alcuni degli esempi di scikit-learn utilizzando la struttura e l'analisi dei dati.
Installazione
Se hai già installato NumPy e Scipy, di seguito sono riportati i due modi più semplici per installare scikit-learn:
Utilizzando pip
Il seguente comando può essere utilizzato per installare scikit-learn tramite pip -
pip install -U scikit-learnUtilizzando conda
Il seguente comando può essere utilizzato per installare scikit-learn tramite conda -
conda install scikit-learnD'altra parte, se NumPy e Scipy non sono ancora installati sulla tua workstation Python, puoi installarli utilizzando uno dei due pip o conda.
Un'altra opzione per usare scikit-learn è usare distribuzioni Python come Canopy e Anaconda perché entrambi forniscono l'ultima versione di scikit-learn.
Caratteristiche
Piuttosto che concentrarsi sul caricamento, la manipolazione e il riepilogo dei dati, la libreria Scikit-learn si concentra sulla modellazione dei dati. Alcuni dei gruppi di modelli più popolari forniti da Sklearn sono i seguenti:
Supervised Learning algorithms - Quasi tutti i più diffusi algoritmi di apprendimento supervisionato, come la regressione lineare, la Support Vector Machine (SVM), l'albero decisionale ecc., Fanno parte di scikit-learn.
Unsupervised Learning algorithms - D'altra parte, ha anche tutti i più diffusi algoritmi di apprendimento non supervisionato dal clustering, analisi fattoriale, PCA (Principal Component Analysis) alle reti neurali non supervisionate.
Clustering - Questo modello viene utilizzato per raggruppare i dati senza etichetta.
Cross Validation - Viene utilizzato per verificare l'accuratezza dei modelli supervisionati su dati invisibili.
Dimensionality Reduction - Viene utilizzato per ridurre il numero di attributi nei dati che possono essere ulteriormente utilizzati per il riepilogo, la visualizzazione e la selezione delle caratteristiche.
Ensemble methods - Come suggerisce il nome, viene utilizzato per combinare le previsioni di più modelli supervisionati.
Feature extraction - Viene utilizzato per estrarre le caratteristiche dai dati per definire gli attributi nei dati di immagine e testo.
Feature selection - Viene utilizzato per identificare attributi utili per creare modelli supervisionati.
Open Source - È una libreria open source e utilizzabile anche commercialmente con licenza BSD.
Questo capitolo tratta il processo di modellazione coinvolto in Sklearn. Cerchiamo di capire lo stesso in dettaglio e iniziare con il caricamento del set di dati.
Caricamento del set di dati
Una raccolta di dati è denominata set di dati. Ha i seguenti due componenti:
Features- Le variabili dei dati sono chiamate le sue caratteristiche. Sono anche noti come predittori, input o attributi.
Feature matrix - È la raccolta di funzionalità, nel caso ce ne siano più di una.
Feature Names - È l'elenco di tutti i nomi delle funzionalità.
Response- È la variabile di output che dipende fondamentalmente dalle variabili delle caratteristiche. Sono anche conosciuti come destinazione, etichetta o output.
Response Vector- Viene utilizzato per rappresentare la colonna di risposta. In genere, abbiamo solo una colonna di risposta.
Target Names - Rappresenta i possibili valori assunti da un vettore di risposta.
Scikit-learn ha pochi set di dati di esempio come iris e digits per la classificazione e il Boston house prices per la regressione.
Esempio
Di seguito è riportato un esempio da caricare iris set di dati -
from sklearn.datasets import load_iris
iris = load_iris()
X = iris.data
y = iris.target
feature_names = iris.feature_names
target_names = iris.target_names
print("Feature names:", feature_names)
print("Target names:", target_names)
print("\nFirst 10 rows of X:\n", X[:10])Produzione
Feature names: ['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']
Target names: ['setosa' 'versicolor' 'virginica']
First 10 rows of X:
[
[5.1 3.5 1.4 0.2]
[4.9 3. 1.4 0.2]
[4.7 3.2 1.3 0.2]
[4.6 3.1 1.5 0.2]
[5. 3.6 1.4 0.2]
[5.4 3.9 1.7 0.4]
[4.6 3.4 1.4 0.3]
[5. 3.4 1.5 0.2]
[4.4 2.9 1.4 0.2]
[4.9 3.1 1.5 0.1]
]Divisione del set di dati
Per verificare l'accuratezza del nostro modello, possiamo dividere il set di dati in due parti:a training set e a testing set. Utilizzare il set di addestramento per addestrare il modello e il set di test per testare il modello. Dopodiché, possiamo valutare il rendimento del nostro modello.
Esempio
Il seguente esempio suddividerà i dati in un rapporto 70:30, ovvero il 70% dei dati verrà utilizzato come dati di addestramento e il 30% verrà utilizzato come dati di test. Il set di dati è il set di dati dell'iride come nell'esempio precedente.
from sklearn.datasets import load_iris
iris = load_iris()
X = iris.data
y = iris.target
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size = 0.3, random_state = 1
)
print(X_train.shape)
print(X_test.shape)
print(y_train.shape)
print(y_test.shape)Produzione
(105, 4)
(45, 4)
(105,)
(45,)Come visto nell'esempio sopra, utilizza train_test_split()funzione di scikit-learn per dividere il set di dati. Questa funzione ha i seguenti argomenti:
X, y - Qui, X è il feature matrix e y è il response vector, che devono essere divisi.
test_size- Questo rappresenta il rapporto tra i dati del test e il totale dei dati forniti. Come nell'esempio precedente, stiamo impostandotest_data = 0.3 per 150 righe di X. Produrrà dati di test di 150 * 0,3 = 45 righe.
random_size- Viene utilizzato per garantire che la divisione sarà sempre la stessa. Ciò è utile nelle situazioni in cui si desidera ottenere risultati riproducibili.
Addestra il modello
Successivamente, possiamo utilizzare il nostro set di dati per addestrare alcuni modelli di previsione. Come discusso, scikit-learn ha un'ampia gamma di fileMachine Learning (ML) algorithms che hanno un'interfaccia coerente per l'adattamento, la previsione dell'accuratezza, il richiamo, ecc.
Esempio
Nell'esempio seguente, utilizzeremo il classificatore KNN (K vicini più vicini). Non entrare nei dettagli degli algoritmi KNN, poiché ci sarà un capitolo separato per questo. Questo esempio viene utilizzato per farti capire solo la parte di implementazione.
from sklearn.datasets import load_iris
iris = load_iris()
X = iris.data
y = iris.target
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size = 0.4, random_state=1
)
from sklearn.neighbors import KNeighborsClassifier
from sklearn import metrics
classifier_knn = KNeighborsClassifier(n_neighbors = 3)
classifier_knn.fit(X_train, y_train)
y_pred = classifier_knn.predict(X_test)
# Finding accuracy by comparing actual response values(y_test)with predicted response value(y_pred)
print("Accuracy:", metrics.accuracy_score(y_test, y_pred))
# Providing sample data and the model will make prediction out of that data
sample = [[5, 5, 3, 2], [2, 4, 3, 5]]
preds = classifier_knn.predict(sample)
pred_species = [iris.target_names[p] for p in preds] print("Predictions:", pred_species)Produzione
Accuracy: 0.9833333333333333
Predictions: ['versicolor', 'virginica']Persistenza del modello
Una volta addestrato il modello, è auspicabile che il modello sia persistente per un utilizzo futuro in modo da non doverlo riaddestrare più e più volte. Può essere fatto con l'aiuto didump e load caratteristiche di joblib pacchetto.
Considera l'esempio seguente in cui salveremo il modello addestrato sopra (classifier_knn) per un uso futuro -
from sklearn.externals import joblib
joblib.dump(classifier_knn, 'iris_classifier_knn.joblib')Il codice precedente salverà il modello nel file denominato iris_classifier_knn.joblib. Ora l'oggetto può essere ricaricato dal file con l'aiuto del seguente codice:
joblib.load('iris_classifier_knn.joblib')Pre-elaborazione dei dati
Poiché abbiamo a che fare con molti dati e quei dati sono in forma grezza, prima di inserire tali dati in algoritmi di apprendimento automatico, dobbiamo convertirli in dati significativi. Questo processo è chiamato pre-elaborazione dei dati. Scikit-learn ha il pacchetto denominatopreprocessingper questo scopo. Ilpreprocessing pacchetto ha le seguenti tecniche:
Binarizzazione
Questa tecnica di pre-elaborazione viene utilizzata quando è necessario convertire i nostri valori numerici in valori booleani.
Esempio
import numpy as np
from sklearn import preprocessing
Input_data = np.array(
[2.1, -1.9, 5.5],
[-1.5, 2.4, 3.5],
[0.5, -7.9, 5.6],
[5.9, 2.3, -5.8]]
)
data_binarized = preprocessing.Binarizer(threshold=0.5).transform(input_data)
print("\nBinarized data:\n", data_binarized)Nell'esempio sopra, abbiamo usato threshold value = 0,5 ed è per questo che tutti i valori superiori a 0,5 verrebbero convertiti in 1 e tutti i valori inferiori a 0,5 sarebbero convertiti in 0.
Produzione
Binarized data:
[
[ 1. 0. 1.]
[ 0. 1. 1.]
[ 0. 0. 1.]
[ 1. 1. 0.]
]Rimozione media
Questa tecnica viene utilizzata per eliminare la media dal vettore delle caratteristiche in modo che ogni caratteristica sia centrata sullo zero.
Esempio
import numpy as np
from sklearn import preprocessing
Input_data = np.array(
[2.1, -1.9, 5.5],
[-1.5, 2.4, 3.5],
[0.5, -7.9, 5.6],
[5.9, 2.3, -5.8]]
)
#displaying the mean and the standard deviation of the input data
print("Mean =", input_data.mean(axis=0))
print("Stddeviation = ", input_data.std(axis=0))
#Removing the mean and the standard deviation of the input data
data_scaled = preprocessing.scale(input_data)
print("Mean_removed =", data_scaled.mean(axis=0))
print("Stddeviation_removed =", data_scaled.std(axis=0))Produzione
Mean = [ 1.75 -1.275 2.2 ]
Stddeviation = [ 2.71431391 4.20022321 4.69414529]
Mean_removed = [ 1.11022302e-16 0.00000000e+00 0.00000000e+00]
Stddeviation_removed = [ 1. 1. 1.]Ridimensionamento
Usiamo questa tecnica di pre-elaborazione per ridimensionare i vettori delle caratteristiche. Il ridimensionamento dei vettori delle caratteristiche è importante, perché le caratteristiche non dovrebbero essere sinteticamente grandi o piccole.
Esempio
import numpy as np
from sklearn import preprocessing
Input_data = np.array(
[
[2.1, -1.9, 5.5],
[-1.5, 2.4, 3.5],
[0.5, -7.9, 5.6],
[5.9, 2.3, -5.8]
]
)
data_scaler_minmax = preprocessing.MinMaxScaler(feature_range=(0,1))
data_scaled_minmax = data_scaler_minmax.fit_transform(input_data)
print ("\nMin max scaled data:\n", data_scaled_minmax)Produzione
Min max scaled data:
[
[ 0.48648649 0.58252427 0.99122807]
[ 0. 1. 0.81578947]
[ 0.27027027 0. 1. ]
[ 1. 0.99029126 0. ]
]Normalizzazione
Usiamo questa tecnica di pre-elaborazione per modificare i vettori delle caratteristiche. La normalizzazione dei vettori di caratteristiche è necessaria in modo che i vettori di caratteristiche possano essere misurati su scala comune. Esistono due tipi di normalizzazione come segue:
Normalizzazione L1
È anche chiamato Deviazioni Minime Assolute. Modifica il valore in modo tale che la somma dei valori assoluti rimanga sempre fino a 1 in ogni riga. L'esempio seguente mostra l'implementazione della normalizzazione L1 sui dati di input.
Esempio
import numpy as np
from sklearn import preprocessing
Input_data = np.array(
[
[2.1, -1.9, 5.5],
[-1.5, 2.4, 3.5],
[0.5, -7.9, 5.6],
[5.9, 2.3, -5.8]
]
)
data_normalized_l1 = preprocessing.normalize(input_data, norm='l1')
print("\nL1 normalized data:\n", data_normalized_l1)Produzione
L1 normalized data:
[
[ 0.22105263 -0.2 0.57894737]
[-0.2027027 0.32432432 0.47297297]
[ 0.03571429 -0.56428571 0.4 ]
[ 0.42142857 0.16428571 -0.41428571]
]Normalizzazione L2
Chiamato anche minimi quadrati. Modifica il valore in modo tale che la somma dei quadrati rimanga sempre fino a 1 in ogni riga. L'esempio seguente mostra l'implementazione della normalizzazione L2 sui dati di input.
Esempio
import numpy as np
from sklearn import preprocessing
Input_data = np.array(
[
[2.1, -1.9, 5.5],
[-1.5, 2.4, 3.5],
[0.5, -7.9, 5.6],
[5.9, 2.3, -5.8]
]
)
data_normalized_l2 = preprocessing.normalize(input_data, norm='l2')
print("\nL1 normalized data:\n", data_normalized_l2)Produzione
L2 normalized data:
[
[ 0.33946114 -0.30713151 0.88906489]
[-0.33325106 0.53320169 0.7775858 ]
[ 0.05156558 -0.81473612 0.57753446]
[ 0.68706914 0.26784051 -0.6754239 ]
]Come sappiamo, l'apprendimento automatico sta per creare un modello dai dati. A tal fine, il computer deve prima comprendere i dati. Successivamente, discuteremo vari modi per rappresentare i dati in modo da essere compresi dal computer:
Dati come tabella
Il modo migliore per rappresentare i dati in Scikit-learn è sotto forma di tabelle. Una tabella rappresenta una griglia 2-D di dati in cui le righe rappresentano i singoli elementi del set di dati e le colonne rappresentano le quantità relative a quei singoli elementi.
Esempio
Con l'esempio fornito di seguito, possiamo scaricare iris dataset sotto forma di Pandas DataFrame con l'aiuto di python seaborn biblioteca.
import seaborn as sns
iris = sns.load_dataset('iris')
iris.head()Produzione
sepal_length sepal_width petal_length petal_width species
0 5.1 3.5 1.4 0.2 setosa
1 4.9 3.0 1.4 0.2 setosa
2 4.7 3.2 1.3 0.2 setosa
3 4.6 3.1 1.5 0.2 setosa
4 5.0 3.6 1.4 0.2 setosaDall'output sopra, possiamo vedere che ogni riga di dati rappresenta un singolo fiore osservato e il numero di righe rappresenta il numero totale di fiori nel set di dati. Generalmente, ci riferiamo alle righe della matrice come campioni.
D'altra parte, ogni colonna di dati rappresenta un'informazione quantitativa che descrive ogni campione. Generalmente, ci riferiamo alle colonne della matrice come caratteristiche.
Dati come matrice delle caratteristiche
La matrice delle caratteristiche può essere definita come il layout della tabella in cui le informazioni possono essere pensate come una matrice 2-D. È memorizzato in una variabile denominataXe si presume essere bidimensionale con forma [n_samples, n_features]. Per lo più, è contenuto in un array NumPy o in un Pandas DataFrame. Come detto in precedenza, i campioni rappresentano sempre i singoli oggetti descritti dal dataset e le caratteristiche rappresentano le distinte osservazioni che descrivono ogni campione in maniera quantitativa.
Dati come matrice di destinazione
Insieme alla matrice delle caratteristiche, indicata con X, abbiamo anche l'array di destinazione. Si chiama anche etichetta. È indicato con y. L'etichetta o l'array di destinazione è solitamente unidimensionale con lunghezza n_samples. È generalmente contenuto in NumPyarray o Panda Series. La matrice di destinazione può avere sia i valori, i valori numerici continui che i valori discreti.
In che modo l'array di destinazione differisce dalle colonne delle caratteristiche?
Possiamo distinguere sia per un punto che l'array di destinazione è solitamente la quantità che vogliamo prevedere dai dati, cioè in termini statistici è la variabile dipendente.
Esempio
Nell'esempio seguente, dal set di dati dell'iride prevediamo le specie di fiore in base alle altre misurazioni. In questo caso, la colonna Specie verrebbe considerata come l'elemento.
import seaborn as sns
iris = sns.load_dataset('iris')
%matplotlib inline
import seaborn as sns; sns.set()
sns.pairplot(iris, hue='species', height=3);Produzione
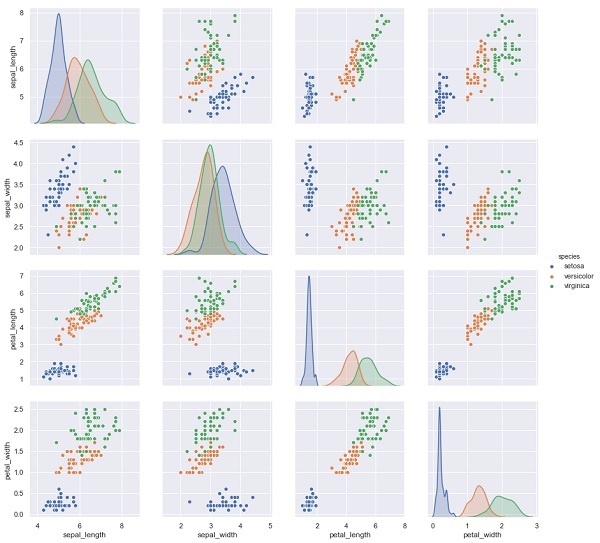
X_iris = iris.drop('species', axis=1)
X_iris.shape
y_iris = iris['species']
y_iris.shapeProduzione
(150,4)
(150,)In questo capitolo impareremo Estimator API(Interfaccia di programmazione applicazioni). Cominciamo con la comprensione di cos'è un'API di stima.
Cos'è Estimator API
È una delle principali API implementate da Scikit-learn. Fornisce un'interfaccia coerente per un'ampia gamma di applicazioni ML, ecco perché tutti gli algoritmi di apprendimento automatico in Scikit-Learn vengono implementati tramite l'API Estimator. L'oggetto che apprende dai dati (adattando i dati) è uno stimatore. Può essere utilizzato con qualsiasi algoritmo come classificazione, regressione, clustering o anche con un trasformatore, che estrae funzionalità utili dai dati grezzi.
Per l'adattamento dei dati, tutti gli oggetti dello stimatore espongono un metodo di adattamento che accetta un set di dati mostrato come segue:
estimator.fit(data)Successivamente, tutti i parametri di uno stimatore possono essere impostati, come segue, quando viene istanziato dall'attributo corrispondente.
estimator = Estimator (param1=1, param2=2)
estimator.param1L'output di quanto sopra sarebbe 1.
Una volta che i dati sono dotati di uno stimatore, i parametri vengono stimati dai dati a portata di mano. Ora, tutti i parametri stimati saranno gli attributi dell'oggetto stimatore che terminano con un trattino basso come segue:
estimator.estimated_param_Utilizzo di Estimator API
Gli usi principali degli stimatori sono i seguenti:
Stima e decodifica di un modello
L'oggetto Estimator viene utilizzato per la stima e la decodifica di un modello. Inoltre, il modello è stimato come una funzione deterministica dei seguenti:
I parametri forniti nella costruzione dell'oggetto.
Lo stato casuale globale (numpy.random) se il parametro random_state dello stimatore è impostato su nessuno.
Tutti i dati passati alla chiamata più recente a fit, fit_transform, or fit_predict.
Tutti i dati passati in una sequenza di chiamate a partial_fit.
Mappatura della rappresentazione dei dati non rettangolari in dati rettangolari
Mappa una rappresentazione di dati non rettangolari in dati rettangolari. In parole semplici, prende l'input in cui ogni campione non è rappresentato come un oggetto simile a una matrice di lunghezza fissa e produce un oggetto di caratteristiche simile a una matrice per ogni campione.
Distinzione tra campioni principali e periferici
Modella la distinzione tra campioni principali e periferici utilizzando i seguenti metodi:
fit
fit_predict se trasduttivo
prevedere se induttivo
Principi guida
Durante la progettazione dell'API Scikit-Learn, tenendo presenti i principi guida:
Consistenza
Questo principio afferma che tutti gli oggetti dovrebbero condividere un'interfaccia comune disegnata da un insieme limitato di metodi. Anche la documentazione dovrebbe essere coerente.
Gerarchia di oggetti limitata
Questo principio guida dice:
Gli algoritmi dovrebbero essere rappresentati da classi Python
I set di dati devono essere rappresentati in formato standard come array NumPy, Pandas DataFrames, matrice sparsa SciPy.
I nomi dei parametri dovrebbero usare stringhe Python standard.
Composizione
Come sappiamo, gli algoritmi ML possono essere espressi come la sequenza di molti algoritmi fondamentali. Scikit-learn fa uso di questi algoritmi fondamentali ogni volta che è necessario.
Valori predefiniti ragionevoli
Secondo questo principio, la libreria Scikit-learn definisce un valore predefinito appropriato ogni volta che i modelli ML richiedono parametri specificati dall'utente.
Ispezione
Secondo questo principio guida, ogni valore di parametro specificato viene esposto come attributi pubici.
Passaggi per l'utilizzo dell'API Estimator
Di seguito sono riportati i passaggi per l'utilizzo dell'API per la stima di Scikit-Learn -
Passaggio 1: scegli una classe di modello
In questo primo passaggio, dobbiamo scegliere una classe di modello. Può essere fatto importando la classe Estimator appropriata da Scikit-learn.
Passaggio 2: scegli gli iperparametri del modello
In questo passaggio, dobbiamo scegliere gli iperparametri del modello di classe. Può essere fatto istanziando la classe con i valori desiderati.
Passaggio 3: disposizione dei dati
Successivamente, dobbiamo organizzare i dati in matrice di caratteristiche (X) e vettore di destinazione (y).
Passaggio 4: adattamento del modello
Ora, dobbiamo adattare il modello ai tuoi dati. Può essere fatto chiamando il metodo fit () dell'istanza del modello.
Passaggio 5: applicazione del modello
Dopo aver adattato il modello, possiamo applicarlo a nuovi dati. Per l'apprendimento supervisionato, utilizzarepredict()metodo per prevedere le etichette per dati sconosciuti. Mentre per l'apprendimento senza supervisione, usapredict() o transform() per dedurre le proprietà dei dati.
Esempio di apprendimento supervisionato
Qui, come esempio di questo processo, stiamo prendendo un caso comune di adattamento di una linea a (x, y) dati, ad es simple linear regression.
Innanzitutto, dobbiamo caricare il set di dati, stiamo usando il set di dati iris -
Esempio
import seaborn as sns
iris = sns.load_dataset('iris')
X_iris = iris.drop('species', axis = 1)
X_iris.shapeProduzione
(150, 4)Esempio
y_iris = iris['species']
y_iris.shapeProduzione
(150,)Esempio
Ora, per questo esempio di regressione, utilizzeremo i seguenti dati di esempio:
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
rng = np.random.RandomState(35)
x = 10*rng.rand(40)
y = 2*x-1+rng.randn(40)
plt.scatter(x,y);Produzione
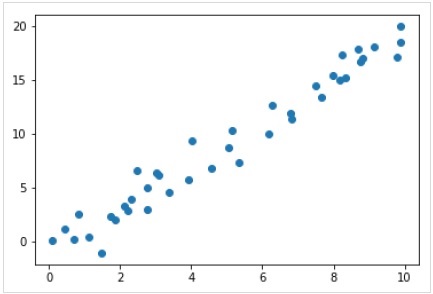
Quindi, abbiamo i dati sopra per il nostro esempio di regressione lineare.
Ora, con questi dati, possiamo applicare i passaggi sopra menzionati.
Scegli una classe di modello
Qui, per calcolare un semplice modello di regressione lineare, dobbiamo importare la classe di regressione lineare come segue:
from sklearn.linear_model import LinearRegressionScegli gli iperparametri del modello
Una volta scelta una classe di modello, dobbiamo fare alcune scelte importanti che sono spesso rappresentate come iperparametri, ovvero i parametri che devono essere impostati prima che il modello si adatti ai dati. Qui, per questo esempio di regressione lineare, vorremmo adattare l'intercetta utilizzando ilfit_intercept iperparametro come segue -
Example
model = LinearRegression(fit_intercept = True)
modelOutput
LinearRegression(copy_X = True, fit_intercept = True, n_jobs = None, normalize = False)Organizzazione dei dati
Ora, come sappiamo che la nostra variabile target y è nella forma corretta, cioè una lunghezza n_samplesmatrice di 1-D. Ma dobbiamo rimodellare la matrice delle caratteristicheX per renderlo una matrice di dimensioni [n_samples, n_features]. Può essere fatto come segue:
Example
X = x[:, np.newaxis]
X.shapeOutput
(40, 1)Modello di montaggio
Una volta sistemati i dati, è il momento di adattare il modello, ovvero di applicare il nostro modello ai dati. Questo può essere fatto con l'aiuto difit() metodo come segue -
Example
model.fit(X, y)Output
LinearRegression(copy_X = True, fit_intercept = True, n_jobs = None,normalize = False)In Scikit-learn, il fit() il processo ha alcuni trattini bassi finali.
Per questo esempio, il parametro seguente mostra la pendenza dell'adattamento lineare semplice dei dati -
Example
model.coef_Output
array([1.99839352])Il parametro seguente rappresenta l'intercetta dell'adattamento lineare semplice ai dati -
Example
model.intercept_Output
-0.9895459457775022Applicazione del modello a nuovi dati
Dopo aver addestrato il modello, possiamo applicarlo a nuovi dati. Poiché il compito principale dell'apprendimento automatico supervisionato è valutare il modello sulla base di nuovi dati che non fanno parte del set di addestramento. Può essere fatto con l'aiuto dipredict() metodo come segue -
Example
xfit = np.linspace(-1, 11)
Xfit = xfit[:, np.newaxis]
yfit = model.predict(Xfit)
plt.scatter(x, y)
plt.plot(xfit, yfit);Output
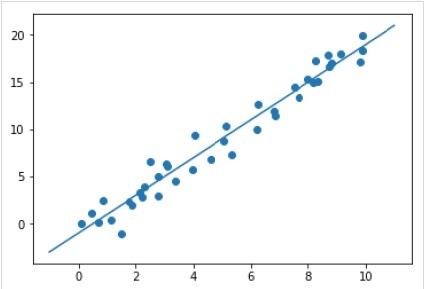
Esempio completo di lavoro / eseguibile
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
iris = sns.load_dataset('iris')
X_iris = iris.drop('species', axis = 1)
X_iris.shape
y_iris = iris['species']
y_iris.shape
rng = np.random.RandomState(35)
x = 10*rng.rand(40)
y = 2*x-1+rng.randn(40)
plt.scatter(x,y);
from sklearn.linear_model import LinearRegression
model = LinearRegression(fit_intercept=True)
model
X = x[:, np.newaxis]
X.shape
model.fit(X, y)
model.coef_
model.intercept_
xfit = np.linspace(-1, 11)
Xfit = xfit[:, np.newaxis]
yfit = model.predict(Xfit)
plt.scatter(x, y)
plt.plot(xfit, yfit);Esempio di apprendimento senza supervisione
Qui, come esempio di questo processo, stiamo prendendo un caso comune di riduzione della dimensionalità del set di dati Iris in modo da poterlo visualizzare più facilmente. Per questo esempio, utilizzeremo l'analisi delle componenti principali (PCA), una tecnica di riduzione della dimensionalità lineare veloce.
Come nell'esempio sopra riportato, possiamo caricare e tracciare i dati casuali dal set di dati iris. Dopodiché possiamo seguire i passaggi come di seguito:
Scegli una classe di modello
from sklearn.decomposition import PCAScegli gli iperparametri del modello
Example
model = PCA(n_components=2)
modelOutput
PCA(copy = True, iterated_power = 'auto', n_components = 2, random_state = None,
svd_solver = 'auto', tol = 0.0, whiten = False)Modello di montaggio
Example
model.fit(X_iris)Output
PCA(copy = True, iterated_power = 'auto', n_components = 2, random_state = None,
svd_solver = 'auto', tol = 0.0, whiten = False)Trasforma i dati in bidimensionali
Example
X_2D = model.transform(X_iris)Ora possiamo tracciare il risultato come segue:
Output
iris['PCA1'] = X_2D[:, 0]
iris['PCA2'] = X_2D[:, 1]
sns.lmplot("PCA1", "PCA2", hue = 'species', data = iris, fit_reg = False);Output
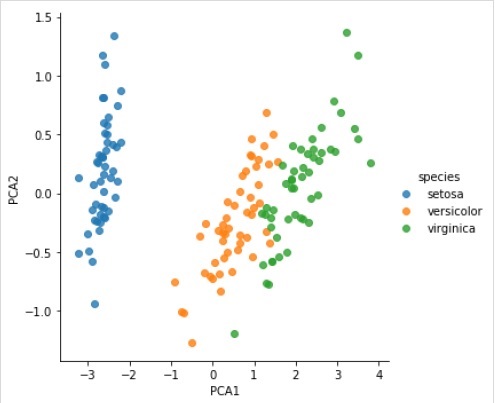
Esempio completo di lavoro / eseguibile
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
iris = sns.load_dataset('iris')
X_iris = iris.drop('species', axis = 1)
X_iris.shape
y_iris = iris['species']
y_iris.shape
rng = np.random.RandomState(35)
x = 10*rng.rand(40)
y = 2*x-1+rng.randn(40)
plt.scatter(x,y);
from sklearn.decomposition import PCA
model = PCA(n_components=2)
model
model.fit(X_iris)
X_2D = model.transform(X_iris)
iris['PCA1'] = X_2D[:, 0]
iris['PCA2'] = X_2D[:, 1]
sns.lmplot("PCA1", "PCA2", hue='species', data=iris, fit_reg=False);Gli oggetti di Scikit-learn condividono un'API di base uniforme che consiste nelle seguenti tre interfacce complementari:
Estimator interface - Serve per costruire e adattare i modelli.
Predictor interface - Serve per fare previsioni.
Transformer interface - Serve per convertire i dati.
Le API adottano convenzioni semplici e le scelte progettuali sono state guidate in modo da evitare la proliferazione del codice del framework.
Scopo delle convenzioni
Lo scopo delle convenzioni è assicurarsi che l'API si attenga ai seguenti principi generali:
Consistency - Tutti gli oggetti, siano essi di base o compositi, devono condividere un'interfaccia coerente composta ulteriormente da un insieme limitato di metodi.
Inspection - I parametri del costruttore ei valori dei parametri determinati dall'algoritmo di apprendimento devono essere archiviati ed esposti come attributi pubblici.
Non-proliferation of classes - I set di dati dovrebbero essere rappresentati come array NumPy o matrice sparsa di Scipy mentre i nomi ei valori degli iperparametri dovrebbero essere rappresentati come stringhe Python standard per evitare la proliferazione del codice del framework.
Composition - Gli algoritmi, sia che siano esprimibili come sequenze o combinazioni di trasformazioni ai dati, sia che siano naturalmente visti come meta-algoritmi parametrizzati su altri algoritmi, dovrebbero essere implementati e composti da blocchi di costruzione esistenti.
Sensible defaults- In scikit-learn ogni volta che un'operazione richiede un parametro definito dall'utente, viene definito un valore predefinito appropriato. Questo valore predefinito dovrebbe far sì che l'operazione venga eseguita in modo ragionevole, ad esempio, fornendo una soluzione di base per l'attività in corso.
Convenzioni varie
Le convenzioni disponibili in Sklearn sono spiegate di seguito:
Tipo casting
Dichiara che l'input deve essere convertito in float64. Nell'esempio seguente, in cuisklearn.random_projection modulo utilizzato per ridurre la dimensionalità dei dati, lo spiegherà -
Example
import numpy as np
from sklearn import random_projection
rannge = np.random.RandomState(0)
X = range.rand(10,2000)
X = np.array(X, dtype = 'float32')
X.dtype
Transformer_data = random_projection.GaussianRandomProjection()
X_new = transformer.fit_transform(X)
X_new.dtypeOutput
dtype('float32')
dtype('float64')Nell'esempio sopra, possiamo vedere che X è float32 a cui viene lanciato float64 di fit_transform(X).
Refitting e aggiornamento dei parametri
Gli iperparametri di uno stimatore possono essere aggiornati e rimontati dopo che è stato costruito tramite il set_params()metodo. Vediamo il seguente esempio per capirlo:
Example
import numpy as np
from sklearn.datasets import load_iris
from sklearn.svm import SVC
X, y = load_iris(return_X_y = True)
clf = SVC()
clf.set_params(kernel = 'linear').fit(X, y)
clf.predict(X[:5])Output
array([0, 0, 0, 0, 0])Una volta che lo stimatore è stato costruito, il codice sopra cambierà il kernel predefinito rbf a lineare via SVC.set_params().
Ora, il codice seguente cambierà nuovamente il kernel in rbf per rimontare lo stimatore e per fare una seconda previsione.
Example
clf.set_params(kernel = 'rbf', gamma = 'scale').fit(X, y)
clf.predict(X[:5])Output
array([0, 0, 0, 0, 0])Codice completo
Quello che segue è il programma eseguibile completo -
import numpy as np
from sklearn.datasets import load_iris
from sklearn.svm import SVC
X, y = load_iris(return_X_y = True)
clf = SVC()
clf.set_params(kernel = 'linear').fit(X, y)
clf.predict(X[:5])
clf.set_params(kernel = 'rbf', gamma = 'scale').fit(X, y)
clf.predict(X[:5])Adattamento Multiclasse e Multilabel
In caso di adattamento multiclasse, sia l'apprendimento che le attività di previsione dipendono dal formato dei dati di destinazione su cui si adattano. Il modulo utilizzato èsklearn.multiclass. Controlla l'esempio seguente, dove il classificatore multiclasse è adatto a un array 1d.
Example
from sklearn.svm import SVC
from sklearn.multiclass import OneVsRestClassifier
from sklearn.preprocessing import LabelBinarizer
X = [[1, 2], [3, 4], [4, 5], [5, 2], [1, 1]]
y = [0, 0, 1, 1, 2]
classif = OneVsRestClassifier(estimator = SVC(gamma = 'scale',random_state = 0))
classif.fit(X, y).predict(X)Output
array([0, 0, 1, 1, 2])Nell'esempio precedente, il classificatore si adatta a una matrice unidimensionale di etichette multiclasse e l'estensione predict()fornisce quindi una previsione multiclasse corrispondente. Ma d'altra parte, è anche possibile adattare una matrice bidimensionale di indicatori di etichette binarie come segue:
Example
from sklearn.svm import SVC
from sklearn.multiclass import OneVsRestClassifier
from sklearn.preprocessing import LabelBinarizer
X = [[1, 2], [3, 4], [4, 5], [5, 2], [1, 1]]
y = LabelBinarizer().fit_transform(y)
classif.fit(X, y).predict(X)Output
array(
[
[0, 0, 0],
[0, 0, 0],
[0, 1, 0],
[0, 1, 0],
[0, 0, 0]
]
)Allo stesso modo, in caso di adattamento di più etichette, a un'istanza possono essere assegnate più etichette come segue:
Example
from sklearn.preprocessing import MultiLabelBinarizer
y = [[0, 1], [0, 2], [1, 3], [0, 2, 3], [2, 4]]
y = MultiLabelBinarizer().fit_transform(y)
classif.fit(X, y).predict(X)Output
array(
[
[1, 0, 1, 0, 0],
[1, 0, 1, 0, 0],
[1, 0, 1, 1, 0],
[1, 0, 1, 1, 0],
[1, 0, 1, 0, 0]
]
)Nell'esempio sopra, sklearn.MultiLabelBinarizerviene utilizzato per binarizzare la matrice bidimensionale di multilabel su cui adattare. Questo è il motivo per cui la funzione Forecast () fornisce un array 2d come output con più etichette per ogni istanza.
Questo capitolo ti aiuterà a conoscere la modellazione lineare in Scikit-Learn. Cominciamo col comprendere cos'è la regressione lineare in Sklearn.
La seguente tabella elenca i vari modelli lineari forniti da Scikit-Learn -
| Suor n | Descrizione del Modello |
|---|---|
| 1 | Regressione lineare È uno dei migliori modelli statistici che studia la relazione tra una variabile dipendente (Y) con un dato insieme di variabili indipendenti (X). |
| 2 | Regressione logistica La regressione logistica, nonostante il nome, è un algoritmo di classificazione piuttosto che un algoritmo di regressione. Basato su un dato insieme di variabili indipendenti, viene utilizzato per stimare il valore discreto (0 o 1, sì / no, vero / falso). |
| 3 | Regressione della cresta La regressione della cresta o regolarizzazione di Tikhonov è la tecnica di regolarizzazione che esegue la regolarizzazione L2. Modifica la funzione di perdita aggiungendo la penalità (quantità di ritiro) equivalente al quadrato della grandezza dei coefficienti. |
| 4 | Regressione bayesiana della cresta La regressione bayesiana consente a un meccanismo naturale di sopravvivere a dati insufficienti o dati scarsamente distribuiti formulando la regressione lineare utilizzando distributori di probabilità piuttosto che stime puntuali. |
| 5 | LASSO LASSO è la tecnica di regolarizzazione che esegue la regolarizzazione L1. Modifica la funzione di perdita aggiungendo la penalità (quantità di ritiro) equivalente alla somma del valore assoluto dei coefficienti. |
| 6 | Multi-task LASSO Consente di adattare più problemi di regressione imponendo congiuntamente che le caratteristiche selezionate siano le stesse per tutti i problemi di regressione, chiamati anche task. Sklearn fornisce un modello lineare denominato MultiTaskLasso, addestrato con una norma mista L1, L2 per la regolarizzazione, che stima i coefficienti sparsi per più problemi di regressione congiuntamente. |
| 7 | Rete elastica Elastic-Net è un metodo di regressione regolarizzato che combina linearmente entrambe le penalità, ovvero L1 e L2 dei metodi di regressione Lazo e Ridge. È utile quando sono presenti più funzionalità correlate. |
| 8 | Rete elastica multi-task Si tratta di un modello Elastic-Net che permette di adattare più problemi di regressione congiuntamente imponendo che le caratteristiche selezionate siano le stesse per tutti i problemi di regressione, chiamati anche task |
Questo capitolo si concentra sulle caratteristiche polinomiali e sugli strumenti di pipelining in Sklearn.
Introduzione alle caratteristiche polinomiali
I modelli lineari addestrati su funzioni non lineari dei dati generalmente mantengono le prestazioni veloci dei metodi lineari. Inoltre, consente loro di adattare una gamma di dati molto più ampia. Questo è il motivo per cui nell'apprendimento automatico vengono utilizzati tali modelli lineari, addestrati su funzioni non lineari.
Uno di questi esempi è che una semplice regressione lineare può essere estesa costruendo caratteristiche polinomiali dai coefficienti.
Matematicamente, supponiamo di avere un modello di regressione lineare standard, quindi per i dati 2-D sarebbe simile a questo:
$$Y=W_{0}+W_{1}X_{1}+W_{2}X_{2}$$Ora possiamo combinare le caratteristiche in polinomi di secondo ordine e il nostro modello avrà il seguente aspetto:
$$Y=W_{0}+W_{1}X_{1}+W_{2}X_{2}+W_{3}X_{1}X_{2}+W_{4}X_1^2+W_{5}X_2^2$$Quanto sopra è ancora un modello lineare. Qui, abbiamo visto che la regressione polinomiale risultante è nella stessa classe di modelli lineari e può essere risolta in modo simile.
Per fare ciò, scikit-learn fornisce un modulo denominato PolynomialFeatures. Questo modulo trasforma una matrice di dati di input in una nuova matrice di dati di un determinato grado.
Parametri
La seguente tabella è costituita dai parametri utilizzati da PolynomialFeatures modulo
| Suor n | Parametro e descrizione |
|---|---|
| 1 | degree - intero, predefinito = 2 Rappresenta il grado delle caratteristiche polinomiali. |
| 2 | interaction_only - Booleano, predefinito = false Per impostazione predefinita, è falso, ma se impostato come vero, vengono prodotte le funzionalità che sono prodotti di funzionalità di input più distinte. Tali funzionalità sono chiamate funzionalità di interazione. |
| 3 | include_bias - Booleano, predefinito = vero Include una colonna di polarizzazione, ovvero la caratteristica in cui tutte le potenze dei polinomi sono zero. |
| 4 | order - str in {'C', 'F'}, default = 'C' Questo parametro rappresenta l'ordine della matrice di output nel caso denso. L'ordine 'F' significa più veloce da calcolare ma d'altra parte, può rallentare gli stimatori successivi. |
Attributi
La tabella seguente è costituita dagli attributi utilizzati da PolynomialFeatures modulo
| Suor n | Attributi e descrizione |
|---|---|
| 1 | powers_ - array, forma (n_output_features, n_input_features) Mostra potenze_ [i, j] è l'esponente del j-esimo input nell'i-esimo output. |
| 2 | n_input_features _ - int Come suggerisce il nome, fornisce il numero totale di funzioni di input. |
| 3 | n_output_features _ - int Come suggerisce il nome, fornisce il numero totale di funzioni di output polinomiali. |
Esempio di implementazione
Seguendo gli usi dello script Python PolynomialFeatures trasformatore per trasformare array di 8 in forma (4,2) -
from sklearn.preprocessing import PolynomialFeatures
import numpy as np
Y = np.arange(8).reshape(4, 2)
poly = PolynomialFeatures(degree=2)
poly.fit_transform(Y)Produzione
array(
[
[ 1., 0., 1., 0., 0., 1.],
[ 1., 2., 3., 4., 6., 9.],
[ 1., 4., 5., 16., 20., 25.],
[ 1., 6., 7., 36., 42., 49.]
]
)Razionalizzazione utilizzando gli strumenti della pipeline
Il tipo di pre-elaborazione di cui sopra, ovvero la trasformazione di una matrice di dati di input in una nuova matrice di dati di un determinato grado, può essere semplificato con il Pipeline strumenti, che sono fondamentalmente utilizzati per concatenare più stimatori in uno.
Esempio
Gli script Python seguenti che utilizzano gli strumenti Pipeline di Scikit-learn per semplificare la preelaborazione (si adatteranno a dati polinomiali di ordine 3).
#First, import the necessary packages.
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.pipeline import Pipeline
import numpy as np
#Next, create an object of Pipeline tool
Stream_model = Pipeline([('poly', PolynomialFeatures(degree=3)), ('linear', LinearRegression(fit_intercept=False))])
#Provide the size of array and order of polynomial data to fit the model.
x = np.arange(5)
y = 3 - 2 * x + x ** 2 - x ** 3
Stream_model = model.fit(x[:, np.newaxis], y)
#Calculate the input polynomial coefficients.
Stream_model.named_steps['linear'].coef_Produzione
array([ 3., -2., 1., -1.])L'output sopra mostra che il modello lineare addestrato sulle caratteristiche polinomiali è in grado di recuperare gli esatti coefficienti polinomiali di input.
Qui, impareremo a conoscere un algoritmo di ottimizzazione in Sklearn, definito come Stochastic Gradient Descent (SGD).
Stochastic Gradient Descent (SGD) è un algoritmo di ottimizzazione semplice ma efficiente utilizzato per trovare i valori dei parametri / coefficienti delle funzioni che minimizzano una funzione di costo. In altre parole, viene utilizzato per l'apprendimento discriminativo di classificatori lineari in funzioni di perdita convessa come SVM e regressione logistica. È stato applicato con successo a set di dati su larga scala perché l'aggiornamento dei coefficienti viene eseguito per ogni istanza di addestramento, piuttosto che alla fine delle istanze.
Classificatore SGD
Il classificatore Stochastic Gradient Descent (SGD) implementa fondamentalmente una semplice routine di apprendimento SGD che supporta varie funzioni di perdita e penalità per la classificazione. Scikit-learn fornisceSGDClassifier modulo per implementare la classificazione SGD.
Parametri
La seguente tabella è costituita dai parametri utilizzati da SGDClassifier modulo -
| Suor n | Parametro e descrizione |
|---|---|
| 1 | loss - str, default = 'hinge' Rappresenta la funzione di perdita da utilizzare durante l'implementazione. Il valore predefinito è "cerniera" che ci darà un SVM lineare. Le altre opzioni che possono essere utilizzate sono:
|
| 2 | penalty - str, "none", "l2", "l1", "elasticnet" È il termine di regolarizzazione utilizzato nel modello. Per impostazione predefinita, è L2. Possiamo usare L1 o 'elasticnet; ma entrambi potrebbero portare scarsità al modello, quindi non ottenibile con L2. |
| 3 | alpha - float, predefinito = 0.0001 Alpha, la costante che moltiplica il termine di regolarizzazione, è il parametro di tuning che decide quanto si vuole penalizzare il modello. Il valore predefinito è 0.0001. |
| 4 | l1_ratio - float, predefinito = 0,15 Questo è chiamato parametro di miscelazione ElasticNet. Il suo range è 0 <= l1_ratio <= 1. Se l1_ratio = 1, la penalità sarebbe L1. Se l1_ratio = 0, la penalità sarebbe una penalità L2. |
| 5 | fit_intercept - Booleano, impostazione predefinita = vero Questo parametro specifica che una costante (bias o intercetta) deve essere aggiunta alla funzione di decisione. Nessuna intercetta verrà utilizzata nel calcolo e i dati saranno considerati già centrati, se verrà impostato su falso. |
| 6 | tol - float o none, opzionale, default = 1.e-3 Questo parametro rappresenta il criterio di arresto per le iterazioni. Il suo valore predefinito è False ma se impostato su Nessuno, le iterazioni si interromperanno quandoloss > best_loss - tol for n_iter_no_changeepoche successive. |
| 7 | shuffle - Booleano, opzionale, predefinito = True Questo parametro indica se vogliamo che i nostri dati di addestramento vengano mescolati dopo ogni epoca o meno. |
| 8 | verbose - intero, predefinito = 0 Rappresenta il livello di verbosità. Il suo valore predefinito è 0. |
| 9 | epsilon - float, predefinito = 0,1 Questo parametro specifica la larghezza della regione insensibile. Se loss = "epsilon-insensitive", qualsiasi differenza tra la previsione corrente e l'etichetta corretta, inferiore alla soglia, verrà ignorata. |
| 10 | max_iter - int, opzionale, default = 1000 Come suggerisce il nome, rappresenta il numero massimo di passaggi nelle epoche, ovvero i dati di allenamento. |
| 11 | warm_start - bool, opzionale, predefinito = false Con questo parametro impostato su True, possiamo riutilizzare la soluzione della chiamata precedente per adattarla all'inizializzazione. Se scegliamo default cioè false, cancellerà la soluzione precedente. |
| 12 | random_state - int, istanza RandomState o None, opzionale, default = nessuno Questo parametro rappresenta il seme del numero pseudo casuale generato che viene utilizzato durante la mescolanza dei dati. Le seguenti sono le opzioni.
|
| 13 | n_jobs - int o none, opzionale, Default = None Rappresenta il numero di CPU da utilizzare nel calcolo OVA (One Versus All), per problemi multi-classe. Il valore predefinito è nessuno, che significa 1. |
| 14 | learning_rate - stringa, opzionale, default = 'ottimale'
|
| 15 | eta0 - doppio, predefinito = 0,0 Rappresenta il tasso di apprendimento iniziale per le opzioni di tasso di apprendimento sopra menzionate, ovvero "costante", "invscalling" o "adattivo". |
| 16 | power_t - idouble, default = 0,5 È l'esponente del tasso di apprendimento "crescente". |
| 17 | early_stopping - bool, predefinito = False Questo parametro rappresenta l'uso dell'arresto anticipato per terminare l'addestramento quando il punteggio di convalida non migliora. Il suo valore predefinito è false ma, se impostato su true, mette automaticamente da parte una frazione stratificata di dati di addestramento come convalida e interrompe l'addestramento quando il punteggio di convalida non migliora. |
| 18 | validation_fraction - float, predefinito = 0,1 Viene utilizzato solo quando early_stopping è vero. Rappresenta la proporzione di dati di addestramento da impostare come set di convalida per la conclusione anticipata dei dati di addestramento. |
| 19 | n_iter_no_change - int, predefinito = 5 Rappresenta il numero di iterazioni senza alcun miglioramento se l'algoritmo dovrebbe essere eseguito prima dell'arresto anticipato. |
| 20 | classs_weight - dict, {class_label: weight} o "balanced", o None, opzionale Questo parametro rappresenta i pesi associati alle classi. Se non fornito, le classi dovrebbero avere un peso 1. |
| 20 | warm_start - bool, opzionale, predefinito = false Con questo parametro impostato su True, possiamo riutilizzare la soluzione della chiamata precedente per adattarla all'inizializzazione. Se scegliamo default cioè false, cancellerà la soluzione precedente. |
| 21 | average - iBoolean o int, opzionale, predefinito = false Rappresenta il numero di CPU da utilizzare nel calcolo OVA (One Versus All), per problemi multi-classe. Il valore predefinito è nessuno, che significa 1. |
Attributi
La tabella seguente è costituita dagli attributi utilizzati da SGDClassifier modulo -
| Suor n | Attributi e descrizione |
|---|---|
| 1 | coef_ - array, shape (1, n_features) if n_classes == 2, else (n_classes, n_features) Questo attributo fornisce il peso assegnato alle caratteristiche. |
| 2 | intercept_ - array, shape (1,) if n_classes == 2, else (n_classes,) Rappresenta il termine indipendente nella funzione decisionale. |
| 3 | n_iter_ - int Fornisce il numero di iterazioni per raggiungere il criterio di arresto. |
Implementation Example
Come altri classificatori, Stochastic Gradient Descent (SGD) deve essere dotato dei seguenti due array:
Un array X contenente i campioni di addestramento. È di dimensione [n_samples, n_features].
Un array Y contenente i valori target, ovvero le etichette di classe per i campioni di addestramento. È di dimensione [n_samples].
Example
Il seguente script Python utilizza il modello lineare SGDClassifier -
import numpy as np
from sklearn import linear_model
X = np.array([[-1, -1], [-2, -1], [1, 1], [2, 1]])
Y = np.array([1, 1, 2, 2])
SGDClf = linear_model.SGDClassifier(max_iter = 1000, tol=1e-3,penalty = "elasticnet")
SGDClf.fit(X, Y)Output
SGDClassifier(
alpha = 0.0001, average = False, class_weight = None,
early_stopping = False, epsilon = 0.1, eta0 = 0.0, fit_intercept = True,
l1_ratio = 0.15, learning_rate = 'optimal', loss = 'hinge', max_iter = 1000,
n_iter = None, n_iter_no_change = 5, n_jobs = None, penalty = 'elasticnet',
power_t = 0.5, random_state = None, shuffle = True, tol = 0.001,
validation_fraction = 0.1, verbose = 0, warm_start = False
)Example
Ora, una volta adattato, il modello può prevedere nuovi valori come segue:
SGDClf.predict([[2.,2.]])Output
array([2])Example
Per l'esempio sopra, possiamo ottenere il vettore di peso con l'aiuto del seguente script python:
SGDClf.coef_Output
array([[19.54811198, 9.77200712]])Example
Allo stesso modo, possiamo ottenere il valore di intercettazione con l'aiuto del seguente script python -
SGDClf.intercept_Output
array([10.])Example
Possiamo ottenere la distanza segnata dall'iperpiano usando SGDClassifier.decision_function come usato nel seguente script python -
SGDClf.decision_function([[2., 2.]])Output
array([68.6402382])Regressore SGD
Il regressore Stochastic Gradient Descent (SGD) implementa fondamentalmente una semplice routine di apprendimento SGD che supporta varie funzioni di perdita e penalità per adattarsi ai modelli di regressione lineare. Scikit-learn fornisceSGDRegressor modulo per implementare la regressione SGD.
Parametri
Parametri utilizzati da SGDRegressorsono quasi uguali a quelli usati nel modulo SGDClassifier. La differenza sta nel parametro "perdita". PerSGDRegressor parametro di perdita dei moduli i valori positivi sono i seguenti:
squared_loss - Si riferisce all'adattamento dei minimi quadrati ordinari.
huber: SGDRegressor- correggere i valori anomali passando dalla perdita quadrata a quella lineare oltre una distanza di epsilon. Il lavoro di "huber" consiste nel modificare "squared_loss" in modo che l'algoritmo si concentri meno sulla correzione dei valori anomali.
epsilon_insensitive - In realtà, ignora gli errori meno di epsilon.
squared_epsilon_insensitive- È uguale a epsilon_insensitive. L'unica differenza è che diventa una perdita quadrata oltre una tolleranza di epsilon.
Un'altra differenza è che il parametro denominato "power_t" ha il valore predefinito di 0,25 anziché 0,5 come in SGDClassifier. Inoltre, non ha i parametri "class_weight" e "n_jobs".
Attributi
Anche gli attributi di SGDRegressor sono gli stessi del modulo SGDClassifier. Piuttosto ha tre attributi extra come segue:
average_coef_ - array, forma (n_features,)
Come suggerisce il nome, fornisce i pesi medi assegnati alle caratteristiche.
average_intercept_ - matrice, forma (1,)
Come suggerisce il nome, fornisce il termine di intercettazione media.
t_ - int
Fornisce il numero di aggiornamenti del peso eseguiti durante la fase di allenamento.
Note - gli attributi average_coef_ e average_intercept_ funzioneranno dopo aver abilitato il parametro 'average' a True.
Implementation Example
Seguendo gli usi dello script Python SGDRegressor modello lineare -
import numpy as np
from sklearn import linear_model
n_samples, n_features = 10, 5
rng = np.random.RandomState(0)
y = rng.randn(n_samples)
X = rng.randn(n_samples, n_features)
SGDReg =linear_model.SGDRegressor(
max_iter = 1000,penalty = "elasticnet",loss = 'huber',tol = 1e-3, average = True
)
SGDReg.fit(X, y)Output
SGDRegressor(
alpha = 0.0001, average = True, early_stopping = False, epsilon = 0.1,
eta0 = 0.01, fit_intercept = True, l1_ratio = 0.15,
learning_rate = 'invscaling', loss = 'huber', max_iter = 1000,
n_iter = None, n_iter_no_change = 5, penalty = 'elasticnet', power_t = 0.25,
random_state = None, shuffle = True, tol = 0.001, validation_fraction = 0.1,
verbose = 0, warm_start = False
)Example
Ora, una volta adattato, possiamo ottenere il vettore di peso con l'aiuto del seguente script python -
SGDReg.coef_Output
array([-0.00423314, 0.00362922, -0.00380136, 0.00585455, 0.00396787])Example
Allo stesso modo, possiamo ottenere il valore di intercettazione con l'aiuto del seguente script python -
SGReg.intercept_Output
SGReg.intercept_Example
Possiamo ottenere il numero di aggiornamenti di peso durante la fase di allenamento con l'aiuto del seguente script python:
SGDReg.t_Output
61.0Pro e contro di SGD
Seguendo i pro di SGD -
Stochastic Gradient Descent (SGD) è molto efficiente.
È molto facile da implementare poiché ci sono molte opportunità per l'ottimizzazione del codice.
A seguito degli svantaggi di SGD -
Stochastic Gradient Descent (SGD) richiede diversi iperparametri come i parametri di regolarizzazione.
È sensibile al ridimensionamento delle funzionalità.
Questo capitolo tratta un metodo di apprendimento automatico denominato SVM (Support Vector Machines).
introduzione
Le Support Vector Machine (SVM) sono metodi di machine learning supervisionati potenti ma flessibili utilizzati per la classificazione, la regressione e il rilevamento dei valori anomali. Gli SVM sono molto efficienti negli spazi ad alta dimensione e generalmente vengono utilizzati nei problemi di classificazione. Gli SVM sono diffusi ed efficienti in termini di memoria perché utilizzano un sottoinsieme di punti di addestramento nella funzione decisionale.
L'obiettivo principale degli SVM è dividere i set di dati in un numero di classi per trovare un file maximum marginal hyperplane (MMH) che può essere fatto nei seguenti due passaggi:
Support Vector Machines genererà prima gli iperpiani in modo iterativo che separa le classi nel modo migliore.
Dopodiché sceglierà l'iperpiano che segrega correttamente le classi.
Alcuni concetti importanti in SVM sono i seguenti:
Support Vectors- Possono essere definiti come i punti dati più vicini all'iperpiano. I vettori di supporto aiutano a decidere la linea di separazione.
Hyperplane - Il piano decisionale o lo spazio che divide un insieme di oggetti aventi classi differenti.
Margin - Il divario tra due linee sui punti dati dell'armadio di classi diverse è chiamato margine.
I seguenti diagrammi ti daranno un'idea di questi concetti SVM:
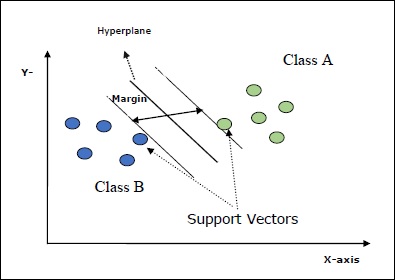
SVM in Scikit-learn supporta vettori campione sia sparsi che densi come input.
Classificazione di SVM
Scikit-learn offre tre classi, vale a dire SVC, NuSVC e LinearSVC che può eseguire la classificazione di classi multiclasse.
SVC
È la classificazione del vettore di supporto C su cui si basa l'implementazione libsvm. Il modulo utilizzato da scikit-learn èsklearn.svm.SVC. Questa classe gestisce il supporto multiclasse secondo uno schema uno contro uno.
Parametri
La seguente tabella è costituita dai parametri utilizzati da sklearn.svm.SVC classe -
| Suor n | Parametro e descrizione |
|---|---|
| 1 | C - float, opzionale, default = 1.0 È il parametro di penalità del termine di errore. |
| 2 | kernel - stringa, opzionale, default = 'rbf' Questo parametro specifica il tipo di kernel da utilizzare nell'algoritmo. possiamo scegliere uno qualsiasi tra,‘linear’, ‘poly’, ‘rbf’, ‘sigmoid’, ‘precomputed’. Il valore predefinito del kernel sarebbe‘rbf’. |
| 3 | degree - int, opzionale, default = 3 Rappresenta il grado della funzione del kernel "poly" e verrà ignorato da tutti gli altri kernel. |
| 4 | gamma - {'scale', 'auto'} o float, È il coefficiente del kernel per i kernel "rbf", "poly" e "sigmoid". |
| 5 | optinal default - = 'scala' Se scegli il valore predefinito, ad esempio gamma = 'scale', il valore di gamma che deve essere utilizzato da SVC è 1 / (_ ∗. ()). D'altra parte, se gamma = 'auto', utilizza 1 / _. |
| 6 | coef0 - float, opzionale, Default = 0.0 Un termine indipendente nella funzione kernel che è significativo solo in "poly" e "sigmoid". |
| 7 | tol - float, opzionale, default = 1.e-3 Questo parametro rappresenta il criterio di arresto per le iterazioni. |
| 8 | shrinking - Booleano, opzionale, predefinito = True Questo parametro rappresenta se vogliamo utilizzare l'euristica di riduzione o meno. |
| 9 | verbose - Booleano, predefinito: false Abilita o disabilita l'output dettagliato. Il suo valore predefinito è false. |
| 10 | probability - booleano, opzionale, predefinito = vero Questo parametro abilita o disabilita le stime di probabilità. Il valore predefinito è false, ma deve essere abilitato prima di chiamare fit. |
| 11 | max_iter - int, opzionale, default = -1 Come suggerisce il nome, rappresenta il numero massimo di iterazioni all'interno del risolutore. Il valore -1 significa che non c'è limite al numero di iterazioni. |
| 12 | cache_size - galleggiante, opzionale Questo parametro specificherà la dimensione della cache del kernel. Il valore sarà in MB (MegaByte). |
| 13 | random_state - int, istanza RandomState o None, opzionale, default = nessuno Questo parametro rappresenta il seme del numero pseudo casuale generato che viene utilizzato durante la mescolanza dei dati. Le seguenti sono le opzioni:
|
| 14 | class_weight - {dict, 'balanced'}, facoltativo Questo parametro imposterà il parametro C della classe j su _ℎ [] ∗ per SVC. Se usiamo l'opzione predefinita, significa che tutte le classi dovrebbero avere un peso. D'altra parte, se scegliclass_weight:balanced, utilizzerà i valori di y per regolare automaticamente i pesi. |
| 15 | decision_function_shape - ovo ',' ovr ', default =' ovr ' Questo parametro deciderà se l'algoritmo tornerà ‘ovr’ (uno contro riposo) funzione decisionale della forma come tutti gli altri classificatori, o l'originale ovo(uno contro uno) funzione decisionale di libsvm. |
| 16 | break_ties - booleano, opzionale, predefinito = false True - La previsione interromperà i legami in base ai valori di confidenza di decision_function False - Il pronostico restituirà la prima classe tra le classi in parità. |
Attributi
La tabella seguente è costituita dagli attributi utilizzati da sklearn.svm.SVC classe -
| Suor n | Attributi e descrizione |
|---|---|
| 1 | support_ - tipo array, forma = [n_SV] Restituisce gli indici dei vettori di supporto. |
| 2 | support_vectors_ - tipo array, forma = [n_SV, n_features] Restituisce i vettori di supporto. |
| 3 | n_support_ - tipo array, dtype = int32, shape = [n_class] Rappresenta il numero di vettori di supporto per ogni classe. |
| 4 | dual_coef_ - matrice, forma = [n_class-1, n_SV] Questi sono i coefficienti dei vettori di supporto nella funzione di decisione. |
| 5 | coef_ - array, forma = [n_class * (n_class-1) / 2, n_features] Questo attributo, disponibile solo in caso di kernel lineare, fornisce il peso assegnato alle funzionalità. |
| 6 | intercept_ - matrice, forma = [n_class * (n_class-1) / 2] Rappresenta il termine indipendente (costante) nella funzione decisionale. |
| 7 | fit_status_ - int L'uscita sarebbe 0 se è montata correttamente. L'uscita sarebbe 1 se non è inserita correttamente. |
| 8 | classes_ - matrice di forma = [n_classes] Fornisce le etichette delle classi. |
Implementation Example
Come altri classificatori, anche SVC deve essere dotato dei seguenti due array:
Un array Xtenendo i campioni di addestramento. È di dimensione [n_samples, n_features].
Un array Ytenendo i valori target, ovvero le etichette di classe per i campioni di addestramento. È di dimensione [n_samples].
Seguendo gli usi dello script Python sklearn.svm.SVC classe -
import numpy as np
X = np.array([[-1, -1], [-2, -1], [1, 1], [2, 1]])
y = np.array([1, 1, 2, 2])
from sklearn.svm import SVC
SVCClf = SVC(kernel = 'linear',gamma = 'scale', shrinking = False,)
SVCClf.fit(X, y)Output
SVC(C = 1.0, cache_size = 200, class_weight = None, coef0 = 0.0,
decision_function_shape = 'ovr', degree = 3, gamma = 'scale', kernel = 'linear',
max_iter = -1, probability = False, random_state = None, shrinking = False,
tol = 0.001, verbose = False)Example
Ora, una volta adattato, possiamo ottenere il vettore di peso con l'aiuto del seguente script python -
SVCClf.coef_Output
array([[0.5, 0.5]])Example
Allo stesso modo, possiamo ottenere il valore di altri attributi come segue:
SVCClf.predict([[-0.5,-0.8]])Output
array([1])Example
SVCClf.n_support_Output
array([1, 1])Example
SVCClf.support_vectors_Output
array(
[
[-1., -1.],
[ 1., 1.]
]
)Example
SVCClf.support_Output
array([0, 2])Example
SVCClf.intercept_Output
array([-0.])Example
SVCClf.fit_status_Output
0NuSVC
NuSVC è Nu Support Vector Classification. È un'altra classe fornita da scikit-learn che può eseguire la classificazione multi-classe. È come SVC ma NuSVC accetta set di parametri leggermente diversi. Il parametro che è diverso da SVC è il seguente:
nu - float, opzionale, default = 0,5
Rappresenta un limite superiore sulla frazione di errori di addestramento e un limite inferiore della frazione di vettori di supporto. Il suo valore dovrebbe essere compreso nell'intervallo (o, 1].
Il resto dei parametri e degli attributi sono gli stessi di SVC.
Esempio di implementazione
Possiamo implementare lo stesso esempio usando sklearn.svm.NuSVC classe anche.
import numpy as np
X = np.array([[-1, -1], [-2, -1], [1, 1], [2, 1]])
y = np.array([1, 1, 2, 2])
from sklearn.svm import NuSVC
NuSVCClf = NuSVC(kernel = 'linear',gamma = 'scale', shrinking = False,)
NuSVCClf.fit(X, y)Produzione
NuSVC(cache_size = 200, class_weight = None, coef0 = 0.0,
decision_function_shape = 'ovr', degree = 3, gamma = 'scale', kernel = 'linear',
max_iter = -1, nu = 0.5, probability = False, random_state = None,
shrinking = False, tol = 0.001, verbose = False)Possiamo ottenere gli output del resto degli attributi come nel caso di SVC.
LinearSVC
È la classificazione del vettore di supporto lineare. È simile a SVC con kernel = 'linear'. La differenza tra loro è questaLinearSVC implementato in termini di liblinear mentre SVC è implementato in libsvm. Questa è la ragioneLinearSVCha una maggiore flessibilità nella scelta delle sanzioni e delle funzioni di perdita. Inoltre si adatta meglio a un numero elevato di campioni.
Se parliamo dei suoi parametri e attributi, allora non supporta ‘kernel’ perché si presume che sia lineare e manca anche di alcuni attributi come support_, support_vectors_, n_support_, fit_status_ e, dual_coef_.
Tuttavia, supporta penalty e loss parametri come segue -
penalty − string, L1 or L2(default = ‘L2’)
Questo parametro viene utilizzato per specificare la norma (L1 o L2) utilizzata nella penalizzazione (regolarizzazione).
loss − string, hinge, squared_hinge (default = squared_hinge)
Rappresenta la funzione di perdita dove "cerniera" è la perdita SVM standard e "squared_hinge" è il quadrato della perdita di cerniera.
Esempio di implementazione
Seguendo gli usi dello script Python sklearn.svm.LinearSVC classe -
from sklearn.svm import LinearSVC
from sklearn.datasets import make_classification
X, y = make_classification(n_features = 4, random_state = 0)
LSVCClf = LinearSVC(dual = False, random_state = 0, penalty = 'l1',tol = 1e-5)
LSVCClf.fit(X, y)Produzione
LinearSVC(C = 1.0, class_weight = None, dual = False, fit_intercept = True,
intercept_scaling = 1, loss = 'squared_hinge', max_iter = 1000,
multi_class = 'ovr', penalty = 'l1', random_state = 0, tol = 1e-05, verbose = 0)Esempio
Ora, una volta adattato, il modello può prevedere nuovi valori come segue:
LSVCClf.predict([[0,0,0,0]])Produzione
[1]Esempio
Per l'esempio sopra, possiamo ottenere il vettore di peso con l'aiuto del seguente script python:
LSVCClf.coef_Produzione
[[0. 0. 0.91214955 0.22630686]]Esempio
Allo stesso modo, possiamo ottenere il valore di intercettazione con l'aiuto del seguente script python -
LSVCClf.intercept_Produzione
[0.26860518]Regressione con SVM
Come discusso in precedenza, SVM viene utilizzato sia per la classificazione che per i problemi di regressione. Il metodo di Scikit-learn di Support Vector Classification (SVC) può essere esteso anche per risolvere i problemi di regressione. Questo metodo esteso è chiamato Support Vector Regression (SVR).
Somiglianza di base tra SVM e SVR
Il modello creato da SVC dipende solo da un sottoinsieme di dati di addestramento. Perché? Perché la funzione di costo per la creazione del modello non si preoccupa dell'addestramento dei punti dati che si trovano al di fuori del margine.
Mentre il modello prodotto da SVR (Support Vector Regression) dipende anche solo da un sottoinsieme dei dati di addestramento. Perché? Perché la funzione di costo per la creazione del modello ignora qualsiasi punto di dati di addestramento vicino alla previsione del modello.
Scikit-learn offre tre classi, vale a dire SVR, NuSVR and LinearSVR come tre diverse implementazioni di SVR.
SVR
È la regressione vettoriale di supporto Epsilon su cui si basa l'implementazione libsvm. Al contrario diSVC Ci sono due parametri liberi nel modello, vale a dire ‘C’ e ‘epsilon’.
epsilon - float, opzionale, default = 0.1
Rappresenta l'epsilon nel modello epsilon-SVR e specifica il tubo epsilon entro il quale nessuna penalità è associata nella funzione di perdita di allenamento con i punti previsti entro una distanza epsilon dal valore effettivo.
Il resto dei parametri e degli attributi sono simili a quelli usati in SVC.
Esempio di implementazione
Seguendo gli usi dello script Python sklearn.svm.SVR classe -
from sklearn import svm
X = [[1, 1], [2, 2]]
y = [1, 2]
SVRReg = svm.SVR(kernel = ’linear’, gamma = ’auto’)
SVRReg.fit(X, y)Produzione
SVR(C = 1.0, cache_size = 200, coef0 = 0.0, degree = 3, epsilon = 0.1, gamma = 'auto',
kernel = 'linear', max_iter = -1, shrinking = True, tol = 0.001, verbose = False)Esempio
Ora, una volta adattato, possiamo ottenere il vettore di peso con l'aiuto del seguente script python -
SVRReg.coef_Produzione
array([[0.4, 0.4]])Esempio
Allo stesso modo, possiamo ottenere il valore di altri attributi come segue:
SVRReg.predict([[1,1]])Produzione
array([1.1])Allo stesso modo, possiamo ottenere anche i valori di altri attributi.
NuSVR
NuSVR è Nu Support Vector Regression. È come NuSVC, ma NuSVR utilizza un parametronuper controllare il numero di vettori di supporto. E inoltre, a differenza di NuSVC dovenu sostituito il parametro C, qui sostituisce epsilon.
Esempio di implementazione
Seguendo gli usi dello script Python sklearn.svm.SVR classe -
from sklearn.svm import NuSVR
import numpy as np
n_samples, n_features = 20, 15
np.random.seed(0)
y = np.random.randn(n_samples)
X = np.random.randn(n_samples, n_features)
NuSVRReg = NuSVR(kernel = 'linear', gamma = 'auto',C = 1.0, nu = 0.1)^M
NuSVRReg.fit(X, y)Produzione
NuSVR(C = 1.0, cache_size = 200, coef0 = 0.0, degree = 3, gamma = 'auto',
kernel = 'linear', max_iter = -1, nu = 0.1, shrinking = True, tol = 0.001,
verbose = False)Esempio
Ora, una volta adattato, possiamo ottenere il vettore di peso con l'aiuto del seguente script python -
NuSVRReg.coef_Produzione
array(
[
[-0.14904483, 0.04596145, 0.22605216, -0.08125403, 0.06564533,
0.01104285, 0.04068767, 0.2918337 , -0.13473211, 0.36006765,
-0.2185713 , -0.31836476, -0.03048429, 0.16102126, -0.29317051]
]
)Allo stesso modo, possiamo ottenere anche il valore di altri attributi.
LinearSVR
È la regressione vettoriale di supporto lineare. È simile a SVR con kernel = 'linear'. La differenza tra loro è questaLinearSVR implementato in termini di liblinear, mentre SVC implementato in libsvm. Questa è la ragioneLinearSVRha una maggiore flessibilità nella scelta delle sanzioni e delle funzioni di perdita. Inoltre si adatta meglio a un numero elevato di campioni.
Se parliamo dei suoi parametri e attributi, allora non supporta ‘kernel’ perché si presume che sia lineare e manca anche di alcuni attributi come support_, support_vectors_, n_support_, fit_status_ e, dual_coef_.
Tuttavia, supporta i parametri di "perdita" come segue:
loss - stringa, opzionale, predefinito = 'epsilon_insensitive'
Rappresenta la funzione di perdita dove la perdita epsilon_insensitive è la perdita L1 e la perdita al quadrato epsilon-insensibile è la perdita L2.
Esempio di implementazione
Seguendo gli usi dello script Python sklearn.svm.LinearSVR classe -
from sklearn.svm import LinearSVR
from sklearn.datasets import make_regression
X, y = make_regression(n_features = 4, random_state = 0)
LSVRReg = LinearSVR(dual = False, random_state = 0,
loss = 'squared_epsilon_insensitive',tol = 1e-5)
LSVRReg.fit(X, y)Produzione
LinearSVR(
C=1.0, dual=False, epsilon=0.0, fit_intercept=True,
intercept_scaling=1.0, loss='squared_epsilon_insensitive',
max_iter=1000, random_state=0, tol=1e-05, verbose=0
)Esempio
Ora, una volta adattato, il modello può prevedere nuovi valori come segue:
LSRReg.predict([[0,0,0,0]])Produzione
array([-0.01041416])Esempio
Per l'esempio sopra, possiamo ottenere il vettore di peso con l'aiuto del seguente script python:
LSRReg.coef_Produzione
array([20.47354746, 34.08619401, 67.23189022, 87.47017787])Esempio
Allo stesso modo, possiamo ottenere il valore di intercettazione con l'aiuto del seguente script python -
LSRReg.intercept_Produzione
array([-0.01041416])Qui impareremo cos'è il rilevamento delle anomalie in Sklearn e come viene utilizzato nell'identificazione dei punti dati.
Il rilevamento delle anomalie è una tecnica utilizzata per identificare i punti dati nel set di dati che non si adattano bene al resto dei dati. Ha molte applicazioni nel business come il rilevamento delle frodi, il rilevamento delle intrusioni, il monitoraggio dell'integrità del sistema, la sorveglianza e la manutenzione predittiva. Le anomalie, chiamate anche valori anomali, possono essere suddivise nelle seguenti tre categorie:
Point anomalies - Si verifica quando una singola istanza di dati è considerata anomala rispetto al resto dei dati.
Contextual anomalies- Questo tipo di anomalia dipende dal contesto. Si verifica se un'istanza di dati è anomala in un contesto specifico.
Collective anomalies - Si verifica quando una raccolta di istanze di dati correlate è anomala rispetto all'intero set di dati anziché ai singoli valori.
Metodi
Due metodi vale a dire outlier detection e novelty detectionpuò essere utilizzato per il rilevamento di anomalie. È necessario vedere la distinzione tra loro.
Rilevamento dei valori anomali
I dati di addestramento contengono valori anomali lontani dal resto dei dati. Tali valori anomali sono definiti come osservazioni. Questo è il motivo per cui gli stimatori del rilevamento dei valori anomali cercano sempre di adattarsi alla regione con i dati di addestramento più concentrati ignorando le osservazioni devianti. È anche noto come rilevamento delle anomalie senza supervisione.
Rilevamento di novità
Si occupa di rilevare un modello non osservato nelle nuove osservazioni che non è incluso nei dati di addestramento. Qui, i dati di allenamento non sono inquinati dai valori anomali. È anche noto come rilevamento di anomalie semi-supervisionato.
Esistono una serie di strumenti ML, forniti da scikit-learn, che possono essere utilizzati sia per il rilevamento dei valori anomali che per il rilevamento delle novità. Questi strumenti implementano prima l'apprendimento degli oggetti dai dati in modo non supervisionato utilizzando il metodo fit () come segue:
estimator.fit(X_train)Ora, le nuove osservazioni verranno ordinate come inliers (labeled 1) o outliers (labeled -1) utilizzando il metodo forecast () come segue:
estimator.fit(X_test)Lo stimatore calcolerà prima la funzione di punteggio non elaborato e quindi il metodo di previsione utilizzerà la soglia su quella funzione di punteggio non elaborato. Possiamo accedere a questa funzione di punteggio grezzo con l'aiuto discore_sample metodo e può controllare la soglia di contamination parametro.
Possiamo anche definire decision_function metodo che definisce valori anomali come valore negativo e valori anomali come valore non negativo.
estimator.decision_function(X_test)Sklearn algoritmi per il rilevamento dei valori anomali
Cominciamo col capire cos'è un involucro ellittico.
Adatto a un involucro ellittico
Questo algoritmo presume che i dati regolari provengano da una distribuzione nota come la distribuzione gaussiana. Per il rilevamento dei valori anomali, Scikit-learn fornisce un oggetto denominatocovariance.EllipticEnvelop.
Questo oggetto adatta una stima robusta di covarianza ai dati e, quindi, adatta un'ellisse ai punti dati centrali. Ignora i punti al di fuori della modalità centrale.
Parametri
La tabella seguente è composta dai parametri utilizzati da sklearn. covariance.EllipticEnvelop metodo -
| Suor n | Parametro e descrizione |
|---|---|
| 1 | store_precision - Booleano, opzionale, predefinito = True Possiamo specificarlo se viene memorizzata la precisione stimata. |
| 2 | assume_centered - Booleano, opzionale, predefinito = False Se impostiamo False, calcolerà la posizione robusta e la covarianza direttamente con l'aiuto dell'algoritmo FastMCD. D'altra parte, se impostato su True, calcolerà il supporto di posizione robusta e covariante. |
| 3 | support_fraction - float in (0., 1.), opzionale, default = Nessuno Questo parametro indica al metodo quanta proporzione di punti deve essere inclusa nel supporto delle stime MCD non elaborate. |
| 4 | contamination - float in (0., 1.), opzionale, default = 0.1 Fornisce la proporzione dei valori anomali nel set di dati. |
| 5 | random_state - int, istanza RandomState o None, opzionale, default = nessuno Questo parametro rappresenta il seme del numero pseudo casuale generato che viene utilizzato durante la mescolanza dei dati. Le seguenti sono le opzioni:
|
Attributi
La tabella seguente è costituita dagli attributi utilizzati da sklearn. covariance.EllipticEnvelop metodo -
| Suor n | Attributi e descrizione |
|---|---|
| 1 | support_ - tipo array, forma (n_samples,) Rappresenta la maschera delle osservazioni utilizzate per calcolare stime robuste di posizione e forma. |
| 2 | location_ - tipo array, forma (n_features) Restituisce la posizione robusta stimata. |
| 3 | covariance_ - tipo array, forma (n_features, n_features) Restituisce la matrice di covarianza robusta stimata. |
| 4 | precision_ - tipo array, forma (n_features, n_features) Restituisce la matrice pseudo inversa stimata. |
| 5 | offset_ - galleggiante Viene utilizzato per definire la funzione decisionale dai punteggi grezzi. decision_function = score_samples -offset_ |
Implementation Example
import numpy as np^M
from sklearn.covariance import EllipticEnvelope^M
true_cov = np.array([[.5, .6],[.6, .4]])
X = np.random.RandomState(0).multivariate_normal(mean = [0, 0], cov=true_cov,size=500)
cov = EllipticEnvelope(random_state = 0).fit(X)^M
# Now we can use predict method. It will return 1 for an inlier and -1 for an outlier.
cov.predict([[0, 0],[2, 2]])Output
array([ 1, -1])Foresta di isolamento
In caso di set di dati ad alta dimensione, un modo efficiente per il rilevamento dei valori anomali consiste nell'utilizzare foreste casuali. Lo scikit-learn fornisceensemble.IsolationForestmetodo che isola le osservazioni selezionando casualmente una caratteristica. Successivamente, seleziona in modo casuale un valore tra i valori massimo e minimo delle caratteristiche selezionate.
In questo caso, il numero di suddivisioni necessarie per isolare un campione è equivalente alla lunghezza del percorso dal nodo radice al nodo terminale.
Parametri
La seguente tabella è costituita dai parametri utilizzati da sklearn. ensemble.IsolationForest metodo -
| Suor n | Parametro e descrizione |
|---|---|
| 1 | n_estimators - int, opzionale, default = 100 Rappresenta il numero di stimatori di base nell'insieme. |
| 2 | max_samples - int o float, opzionale, default = "auto" Rappresenta il numero di campioni da estrarre da X per addestrare ogni stimatore di base. Se scegliamo int come valore, disegnerà max_samples campioni. Se scegliamo float come suo valore, disegnerà max_samples ∗ .shape [0] samples. E, se scegliamo auto come valore, disegnerà max_samples = min (256, n_samples). |
| 3 | support_fraction - float in (0., 1.), opzionale, default = Nessuno Questo parametro indica al metodo quanta proporzione di punti deve essere inclusa nel supporto delle stime MCD non elaborate. |
| 4 | contamination - auto o float, opzionale, default = auto Fornisce la proporzione dei valori anomali nel set di dati. Se lo impostiamo come predefinito, cioè auto, determinerà la soglia come nella carta originale. Se impostato su float, l'intervallo di contaminazione sarà nell'intervallo [0,0.5]. |
| 5 | random_state - int, istanza RandomState o None, opzionale, default = nessuno Questo parametro rappresenta il seme del numero pseudo casuale generato che viene utilizzato durante la mescolanza dei dati. Le seguenti sono le opzioni:
|
| 6 | max_features - int o float, opzionale (default = 1.0) Rappresenta il numero di caratteristiche da trarre da X per addestrare ogni stimatore di base. Se scegliamo int come suo valore, disegnerà max_features caratteristiche. Se scegliamo float come valore, disegnerà max_features * X.shape [] samples. |
| 7 | bootstrap - Booleano, opzionale (predefinito = False) La sua opzione predefinita è False, il che significa che il campionamento verrà eseguito senza sostituzione. E d'altra parte, se impostato su True, significa che i singoli alberi si adattano a un sottoinsieme casuale dei dati di addestramento campionati con la sostituzione. |
| 8 | n_jobs - int o None, opzionale (default = None) Rappresenta il numero di lavori per cui eseguire in parallelo fit() e predict() metodi entrambi. |
| 9 | verbose - int, opzionale (default = 0) Questo parametro controlla la verbosità del processo di creazione dell'albero. |
| 10 | warm_start - Bool, opzionale (default = False) Se warm_start = true, possiamo riutilizzare la soluzione delle chiamate precedenti per adattarla e aggiungere più stimatori all'insieme. Ma se è impostato su false, dobbiamo inserire una foresta completamente nuova. |
Attributi
La tabella seguente è costituita dagli attributi utilizzati da sklearn. ensemble.IsolationForest metodo -
| Suor n | Attributi e descrizione |
|---|---|
| 1 | estimators_ - elenco di DecisionTreeClassifier Fornire la raccolta di tutti i sub-stimatori adattati. |
| 2 | max_samples_ - intero Fornisce il numero effettivo di campioni utilizzati. |
| 3 | offset_ - galleggiante Viene utilizzato per definire la funzione decisionale dai punteggi grezzi. decision_function = score_samples -offset_ |
Implementation Example
Lo script Python di seguito utilizzerà sklearn. ensemble.IsolationForest metodo per adattare 10 alberi su dati dati
from sklearn.ensemble import IsolationForest
import numpy as np
X = np.array([[-1, -2], [-3, -3], [-3, -4], [0, 0], [-50, 60]])
OUTDClf = IsolationForest(n_estimators = 10)
OUTDclf.fit(X)Output
IsolationForest(
behaviour = 'old', bootstrap = False, contamination='legacy',
max_features = 1.0, max_samples = 'auto', n_estimators = 10, n_jobs=None,
random_state = None, verbose = 0
)Fattore anomalo locale
L'algoritmo Local Outlier Factor (LOF) è un altro algoritmo efficiente per eseguire il rilevamento dei valori anomali su dati di grandi dimensioni. Lo scikit-learn fornisceneighbors.LocalOutlierFactormetodo che calcola un punteggio, chiamato fattore di anomalia locale, che riflette il grado di anomalia delle osservazioni. La logica principale di questo algoritmo è quella di rilevare i campioni che hanno una densità sostanzialmente inferiore rispetto ai suoi vicini. Ecco perché misura la deviazione della densità locale di determinati punti dati rispetto ai loro vicini.
Parametri
La seguente tabella è costituita dai parametri utilizzati da sklearn. neighbors.LocalOutlierFactor metodo
| Suor n | Parametro e descrizione |
|---|---|
| 1 | n_neighbors - int, opzionale, predefinito = 20 Rappresenta il numero di vicini utilizzati per impostazione predefinita per la query dei vicini. Tutti i campioni sarebbero usati se. |
| 2 | algorithm - opzionale Quale algoritmo utilizzare per calcolare i vicini più vicini.
|
| 3 | leaf_size - int, opzionale, default = 30 Il valore di questo parametro può influire sulla velocità di costruzione e query. Colpisce anche la memoria richiesta per memorizzare l'albero. Questo parametro viene passato agli algoritmi BallTree o KdTree. |
| 4 | contamination - auto o float, opzionale, default = auto Fornisce la proporzione dei valori anomali nel set di dati. Se lo impostiamo come predefinito, cioè auto, determinerà la soglia come nella carta originale. Se impostato su float, l'intervallo di contaminazione sarà nell'intervallo [0,0.5]. |
| 5 | metric - stringa o richiamabile, predefinito Rappresenta la metrica utilizzata per il calcolo della distanza. |
| 6 | P - int, opzionale (default = 2) È il parametro per la metrica Minkowski. P = 1 equivale a usare manhattan_distance cioè L1, mentre P = 2 equivale a usare euclidean_distance cioè L2. |
| 7 | novelty - Booleano, (predefinito = False) Per impostazione predefinita, l'algoritmo LOF viene utilizzato per il rilevamento dei valori anomali, ma può essere utilizzato per il rilevamento delle novità se impostiamo novità = vero. |
| 8 | n_jobs - int o None, opzionale (default = None) Rappresenta il numero di lavori da eseguire in parallelo sia per i metodi fit () che per i metodi prediction (). |
Attributi
La tabella seguente è costituita dagli attributi utilizzati da sklearn.neighbors.LocalOutlierFactor metodo -
| Suor n | Attributi e descrizione |
|---|---|
| 1 | negative_outlier_factor_ - array numpy, forma (n_samples,) Fornire LOF opposto ai campioni di addestramento. |
| 2 | n_neighbors_ - intero Fornisce il numero effettivo di vicini utilizzati per le query dei vicini. |
| 3 | offset_ - galleggiante Viene utilizzato per definire le etichette binarie dai punteggi grezzi. |
Implementation Example
Lo script Python fornito di seguito utilizzerà sklearn.neighbors.LocalOutlierFactor metodo per costruire la classe NeighborsClassifier da qualsiasi array corrispondente al nostro set di dati
from sklearn.neighbors import NearestNeighbors
samples = [[0., 0., 0.], [0., .5, 0.], [1., 1., .5]]
LOFneigh = NearestNeighbors(n_neighbors = 1, algorithm = "ball_tree",p=1)
LOFneigh.fit(samples)Output
NearestNeighbors(
algorithm = 'ball_tree', leaf_size = 30, metric='minkowski',
metric_params = None, n_jobs = None, n_neighbors = 1, p = 1, radius = 1.0
)Example
Ora, possiamo chiedere a questo classificatore costruito se il punto più vicino a [0.5, 1., 1.5] usando il seguente script python -
print(neigh.kneighbors([[.5, 1., 1.5]])Output
(array([[1.7]]), array([[1]], dtype = int64))SVM di una classe
Il One-Class SVM, introdotto da Schölkopf et al., È il rilevamento dei valori anomali senza supervisione. È anche molto efficiente nei dati ad alta dimensione e stima il supporto di una distribuzione ad alta dimensione. È implementato inSupport Vector Machines modulo in Sklearn.svm.OneClassSVMoggetto. Per definire una frontiera, richiede un kernel (il più usato è RBF) e un parametro scalare.
Per una migliore comprensione adattiamo i nostri dati con svm.OneClassSVM oggetto -
Esempio
from sklearn.svm import OneClassSVM
X = [[0], [0.89], [0.90], [0.91], [1]]
OSVMclf = OneClassSVM(gamma = 'scale').fit(X)Ora possiamo ottenere score_samples per i dati di input come segue:
OSVMclf.score_samples(X)Produzione
array([1.12218594, 1.58645126, 1.58673086, 1.58645127, 1.55713767])Questo capitolo ti aiuterà a comprendere i metodi del vicino più vicino in Sklearn.
Il metodo di apprendimento basato sul vicino è di entrambi i tipi, vale a dire supervised e unsupervised. L'apprendimento basato sui vicini supervisionati può essere utilizzato sia per la classificazione che per i problemi predittivi di regressione, ma viene utilizzato principalmente per la classificazione dei problemi predittivi nell'industria.
I metodi di apprendimento basati sui vicini non hanno una fase di formazione specializzata e utilizzano tutti i dati per l'addestramento durante la classificazione. Inoltre, non presuppone nulla sui dati sottostanti. Questo è il motivo per cui sono di natura pigra e non parametrica.
Il principio principale alla base dei metodi del vicino più vicino è:
Per trovare un numero predefinito di campioni di addestramento vicino al nuovo punto dati
Prevedi l'etichetta da questo numero di campioni di addestramento.
Qui, il numero di campioni può essere una costante definita dall'utente come nell'apprendimento del vicino più prossimo K o variare in base alla densità locale del punto come nell'apprendimento del vicino basato sul raggio.
Modulo sklearn.neighbors
Scikit-learn ha sklearn.neighborsmodulo che fornisce funzionalità per metodi di apprendimento basati sui vicini sia non supervisionati che supervisionati. Come input, le classi in questo modulo possono gestire array NumPy oscipy.sparse matrici.
Tipi di algoritmi
I diversi tipi di algoritmi che possono essere utilizzati nell'implementazione dei metodi basati sui vicini sono i seguenti:
Forza bruta
Il calcolo della forza bruta delle distanze tra tutte le coppie di punti nel set di dati fornisce l'implementazione più ingenua della ricerca dei vicini. Matematicamente, per N campioni in dimensioni D, l'approccio a forza bruta scala come0[DN2]
Per piccoli campioni di dati, questo algoritmo può essere molto utile, ma diventa irrealizzabile man mano che il numero di campioni aumenta. La ricerca del vicino di forza bruta può essere abilitata scrivendo la parola chiavealgorithm=’brute’.
KD Tree
Una delle strutture di dati ad albero che sono state inventate per affrontare le inefficienze computazionali dell'approccio a forza bruta è la struttura di dati ad albero KD. Fondamentalmente, l'albero KD è una struttura ad albero binario chiamata albero K-dimensionale. Partiziona ricorsivamente lo spazio dei parametri lungo gli assi dei dati dividendolo in regioni ortografiche annidate in cui vengono riempiti i punti dati.
Vantaggi
Di seguito sono riportati alcuni vantaggi dell'algoritmo dell'albero KD:
Construction is fast - Poiché il partizionamento viene eseguito solo lungo gli assi dei dati, la costruzione dell'albero di KD è molto veloce.
Less distance computations- Questo algoritmo richiede calcoli di distanza molto inferiori per determinare il vicino più vicino di un punto di query. Ci vuole solo[ ()] calcoli della distanza.
Svantaggi
Fast for only low-dimensional neighbor searches- È molto veloce per le ricerche di vicini di bassa dimensione (D <20) ma man mano che D cresce diventa inefficiente. Poiché il partizionamento viene eseguito solo lungo gli assi dei dati,
Le ricerche nei vicini dell'albero di KD possono essere abilitate scrivendo la parola chiave algorithm=’kd_tree’.
Palla Albero
Poiché sappiamo che KD Tree è inefficiente nelle dimensioni superiori, quindi, per affrontare questa inefficienza di KD Tree, è stata sviluppata la struttura dati Ball tree. Matematicamente, divide ricorsivamente i dati, in nodi definiti da un centroide C e raggio r, in modo tale che ogni punto nel nodo si trovi all'interno dell'ipersfera definita dal centroideC e raggio r. Utilizza la disuguaglianza triangolare, indicata di seguito, che riduce il numero di punti candidati per una ricerca di vicini
$$\arrowvert X+Y\arrowvert\leq \arrowvert X\arrowvert+\arrowvert Y\arrowvert$$Vantaggi
Di seguito sono riportati alcuni vantaggi dell'algoritmo Ball Tree:
Efficient on highly structured data - Poiché l'albero della sfera divide i dati in una serie di iper-sfere di nidificazione, è efficiente su dati altamente strutturati.
Out-performs KD-tree - L'albero della palla supera l'albero KD nelle dimensioni elevate perché ha una geometria sferica dei nodi dell'albero della palla.
Svantaggi
Costly - La suddivisione dei dati in una serie di iper-sfere di nidificazione rende la sua costruzione molto costosa.
È possibile abilitare le ricerche sui vicini dell'albero della palla scrivendo la parola chiave algorithm=’ball_tree’.
Scelta dell'algoritmo dei vicini più vicini
La scelta di un algoritmo ottimale per un dato set di dati dipende dai seguenti fattori:
Numero di campioni (N) e dimensionalità (D)
Questi sono i fattori più importanti da considerare quando si sceglie l'algoritmo Nearest Neighbor. È a causa dei motivi indicati di seguito:
Il tempo di query dell'algoritmo Brute Force cresce come O [DN].
Il tempo di interrogazione dell'algoritmo Ball tree cresce come O [D log (N)].
Il tempo di interrogazione dell'algoritmo dell'albero KD cambia con D in un modo strano che è molto difficile da caratterizzare. Quando D <20, il costo è O [D log (N)] e questo algoritmo è molto efficiente. D'altra parte, è inefficiente nel caso in cui D> 20 perché il costo aumenta fino a quasi O [DN].
Struttura dati
Un altro fattore che influenza le prestazioni di questi algoritmi è la dimensionalità intrinseca dei dati o la scarsità dei dati. È perché i tempi di interrogazione degli algoritmi Ball tree e KD tree possono essere notevolmente influenzati da esso. Considerando che, il tempo di query dell'algoritmo Brute Force è invariato dalla struttura dei dati. In generale, gli algoritmi Ball tree e KD tree producono tempi di query più rapidi se impiantati su dati più scarsi con dimensionalità intrinseca più piccola.
Numero di vicini (k)
Il numero di vicini (k) richiesti per un punto di interrogazione influisce sul tempo di interrogazione degli algoritmi di Ball tree e KD tree. Il loro tempo di interrogazione diventa più lento all'aumentare del numero di vicini (k). Considerando che il tempo di query di Brute Force rimarrà inalterato dal valore di k.
Numero di punti di query
Poiché hanno bisogno di una fase di costruzione, sia gli algoritmi KD tree che Ball tree saranno efficaci se il numero di punti di interrogazione è elevato. D'altra parte, se c'è un numero inferiore di punti di query, l'algoritmo Brute Force funziona meglio degli algoritmi KD tree e Ball tree.
k-NN (k-Nearest Neighbor), uno dei più semplici algoritmi di machine learning, non è parametrico e di natura pigra. Non parametrico significa che non vi è alcuna ipotesi per la distribuzione dei dati sottostante, ovvero la struttura del modello è determinata dal set di dati. L'apprendimento lento o basato sull'istanza significa che ai fini della generazione del modello, non richiede alcun punto dati di addestramento e nella fase di test vengono utilizzati dati di addestramento completi.
L'algoritmo k-NN consiste nei seguenti due passaggi:
Passo 1
In questo passaggio, calcola e memorizza i k vicini più vicini per ogni campione nel set di addestramento.
Passo 2
In questo passaggio, per un campione senza etichetta, recupera i k vicini più vicini dal set di dati. Quindi tra questi vicini k-più vicini, predice la classe attraverso il voto (la classe con la maggioranza dei voti vince).
Il modulo, sklearn.neighbors che implementa l'algoritmo dei vicini k-più vicini, fornisce la funzionalità per unsupervised così come supervised metodi di apprendimento basati sui vicini.
I vicini più vicini senza supervisione implementano algoritmi diversi (BallTree, KDTree o Brute Force) per trovare i vicini più vicini per ogni campione. Questa versione senza supervisione è fondamentalmente solo il passaggio 1, discusso sopra, e la base di molti algoritmi (KNN e K-significa essere il famoso) che richiedono la ricerca del vicino. In parole semplici, è uno studente senza supervisione per l'implementazione delle ricerche sui vicini.
D'altra parte, l'apprendimento basato sui vicini supervisionati viene utilizzato per la classificazione e per la regressione.
Apprendimento KNN senza supervisione
Come discusso, esistono molti algoritmi come KNN e K-Means che richiedono ricerche sul vicino più vicino. Questo è il motivo per cui Scikit-learn ha deciso di implementare la parte di ricerca dei vicini come un proprio "studente". Il motivo alla base della ricerca del vicino come studente separato è che calcolare tutte le distanze a coppie per trovare un vicino più vicino non è ovviamente molto efficiente. Vediamo il modulo utilizzato da Sklearn per implementare l'apprendimento del vicino più vicino senza supervisione insieme all'esempio.
Modulo di apprendimento scikit
sklearn.neighbors.NearestNeighborsè il modulo utilizzato per implementare l'apprendimento del vicino più vicino senza supervisione. Utilizza algoritmi specifici del vicino più vicino denominati BallTree, KDTree o Brute Force. In altre parole, funge da interfaccia uniforme per questi tre algoritmi.
Parametri
La seguente tabella è costituita dai parametri utilizzati da NearestNeighbors modulo -
| Suor n | Parametro e descrizione |
|---|---|
| 1 | n_neighbors - int, opzionale Il numero di vicini da ottenere. Il valore predefinito è 5. |
| 2 | radius - galleggiante, opzionale Limita la distanza dei vicini di ritorno. Il valore predefinito è 1.0. |
| 3 | algorithm - {'auto', 'ball_tree', 'kd_tree', 'brute'}, facoltativo Questo parametro prenderà l'algoritmo (BallTree, KDTree o Brute-force) che desideri utilizzare per calcolare i vicini più vicini. Se fornisci "auto", tenterà di decidere l'algoritmo più appropriato in base ai valori passati al metodo di adattamento. |
| 4 | leaf_size - int, opzionale Può influenzare la velocità di costruzione e interrogazione, nonché la memoria richiesta per memorizzare l'albero. Viene passato a BallTree o KDTree. Sebbene il valore ottimale dipenda dalla natura del problema, il suo valore predefinito è 30. |
| 5 | metric - stringa o richiamabile È la metrica da utilizzare per il calcolo della distanza tra i punti. Possiamo passarlo come stringa o funzione richiamabile. In caso di funzione richiamabile, la metrica viene chiamata su ciascuna coppia di righe e il valore risultante viene registrato. È meno efficiente rispetto al passaggio del nome della metrica come stringa. Possiamo scegliere tra metric da scikit-learn o scipy.spatial.distance. i valori validi sono i seguenti - Scikit-learn - ["cosine", "manhattan", "Euclidean", "l1", "l2", "cityblock"] Scipy.spatial.distance - ["braycurtis", "canberra", "chebyshev", "dice", "hamming", "jaccard", "correlation", "kulsinski", "mahalanobis", "minkowski", "rogerstanimoto", "russellrao", " sokalmicheme "," sokalsneath "," seuclidean "," sqeuclidean "," yule "]. La metrica predefinita è "Minkowski". |
| 6 | P - intero, opzionale È il parametro per la metrica Minkowski. Il valore predefinito è 2, che equivale a utilizzare Euclidean_distance (l2). |
| 7 | metric_params - dict, opzionale Questi sono gli argomenti della parola chiave aggiuntivi per la funzione metrica. Il valore predefinito è Nessuno. |
| 8 | N_jobs - int o None, opzionale Ripropone il numero di lavori paralleli da eseguire per la ricerca dei vicini. Il valore predefinito è Nessuno. |
Implementation Example
L'esempio seguente troverà i vicini più vicini tra due set di dati utilizzando il sklearn.neighbors.NearestNeighbors modulo.
Per prima cosa, dobbiamo importare il modulo e i pacchetti richiesti -
from sklearn.neighbors import NearestNeighbors
import numpy as npOra, dopo aver importato i pacchetti, definisci i set di dati tra i quali vogliamo trovare i vicini più vicini -
Input_data = np.array([[-1, 1], [-2, 2], [-3, 3], [1, 2], [2, 3], [3, 4],[4, 5]])Successivamente, applica l'algoritmo di apprendimento senza supervisione, come segue:
nrst_neigh = NearestNeighbors(n_neighbors = 3, algorithm = 'ball_tree')Quindi, adattare il modello con il set di dati di input.
nrst_neigh.fit(Input_data)Ora, trova i K-vicini del set di dati. Restituirà gli indici e le distanze dei vicini di ogni punto.
distances, indices = nbrs.kneighbors(Input_data)
indicesOutput
array(
[
[0, 1, 3],
[1, 2, 0],
[2, 1, 0],
[3, 4, 0],
[4, 5, 3],
[5, 6, 4],
[6, 5, 4]
], dtype = int64
)
distancesOutput
array(
[
[0. , 1.41421356, 2.23606798],
[0. , 1.41421356, 1.41421356],
[0. , 1.41421356, 2.82842712],
[0. , 1.41421356, 2.23606798],
[0. , 1.41421356, 1.41421356],
[0. , 1.41421356, 1.41421356],
[0. , 1.41421356, 2.82842712]
]
)L'output sopra mostra che il vicino più vicino di ogni punto è il punto stesso, cioè a zero. È perché il set di query corrisponde al set di addestramento.
Example
Possiamo anche mostrare una connessione tra punti vicini producendo un grafico sparse come segue:
nrst_neigh.kneighbors_graph(Input_data).toarray()Output
array(
[
[1., 1., 0., 1., 0., 0., 0.],
[1., 1., 1., 0., 0., 0., 0.],
[1., 1., 1., 0., 0., 0., 0.],
[1., 0., 0., 1., 1., 0., 0.],
[0., 0., 0., 1., 1., 1., 0.],
[0., 0., 0., 0., 1., 1., 1.],
[0., 0., 0., 0., 1., 1., 1.]
]
)Una volta sistemati i non supervisionati NearestNeighbors model, i dati verranno memorizzati in una struttura dati basata sul valore impostato per l'argomento ‘algorithm’. Dopodiché possiamo usare questo studente senza supervisionekneighbors in un modello che richiede ricerche di vicini.
Complete working/executable program
from sklearn.neighbors import NearestNeighbors
import numpy as np
Input_data = np.array([[-1, 1], [-2, 2], [-3, 3], [1, 2], [2, 3], [3, 4],[4, 5]])
nrst_neigh = NearestNeighbors(n_neighbors = 3, algorithm='ball_tree')
nrst_neigh.fit(Input_data)
distances, indices = nbrs.kneighbors(Input_data)
indices
distances
nrst_neigh.kneighbors_graph(Input_data).toarray()Apprendimento KNN supervisionato
L'apprendimento basato sui vicini supervisionati viene utilizzato per:
- Classificazione, per i dati con etichette discrete
- Regressione, per i dati con etichette continue.
Classificatore vicino più vicino
Possiamo comprendere la classificazione basata sui vicini con l'aiuto delle seguenti due caratteristiche:
- Viene calcolato da un voto a maggioranza semplice dei vicini più prossimi di ogni punto.
- Memorizza semplicemente istanze dei dati di addestramento, ecco perché è un tipo di apprendimento non generalizzante.
Moduli di apprendimento scikit
I seguenti sono i due diversi tipi di classificatori del vicino più vicino usati da scikit-learn -
| S.No. | Classificatori e descrizione |
|---|---|
| 1. | KNeighborsClassifier La K nel nome di questo classificatore rappresenta i k vicini più vicini, dove k è un valore intero specificato dall'utente. Quindi, come suggerisce il nome, questo classificatore implementa l'apprendimento basato sui k vicini più vicini. La scelta del valore di k dipende dai dati. |
| 2. | RadiusNeighborsClassifier Il raggio nel nome di questo classificatore rappresenta i vicini più vicini all'interno di un raggio specificato r, dove r è un valore a virgola mobile specificato dall'utente. Quindi, come suggerisce il nome, questo classificatore implementa l'apprendimento in base al numero di vicini entro un raggio fisso r di ciascun punto di addestramento. |
Nearest Neighbor Regressor
Viene utilizzato nei casi in cui le etichette dei dati sono di natura continua. Le etichette dati assegnate vengono calcolate sulla base della media delle etichette dei suoi vicini più prossimi.
I seguenti sono i due diversi tipi di regressori del vicino più vicino usati da scikit-learn -
KNeighborsRegressor
La K nel nome di questo regressore rappresenta i k vicini più vicini, dove k è un integer valuespecificato dall'utente. Quindi, come suggerisce il nome, questo regressore implementa l'apprendimento basato sui k vicini più vicini. La scelta del valore di k dipende dai dati. Comprendiamolo meglio con l'aiuto di un esempio di implementazione.
I seguenti sono i due diversi tipi di regressori del vicino più vicino usati da scikit-learn -
Esempio di implementazione
In questo esempio, implementeremo KNN sul set di dati denominato Iris Flower data set utilizzando scikit-learn KNeighborsRegressor.
Innanzitutto, importa il set di dati dell'iride come segue:
from sklearn.datasets import load_iris
iris = load_iris()Ora, dobbiamo suddividere i dati in dati di addestramento e test. Useremo Sklearntrain_test_split funzione per dividere i dati nel rapporto di 70 (dati di addestramento) e 20 (dati di prova) -
X = iris.data[:, :4]
y = iris.target
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.20)Successivamente, eseguiremo il ridimensionamento dei dati con l'aiuto del modulo di pre-elaborazione Sklearn come segue:
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(X_train)
X_train = scaler.transform(X_train)
X_test = scaler.transform(X_test)Quindi, importa il file KNeighborsRegressor class da Sklearn e fornire il valore dei vicini come segue.
Esempio
import numpy as np
from sklearn.neighbors import KNeighborsRegressor
knnr = KNeighborsRegressor(n_neighbors = 8)
knnr.fit(X_train, y_train)Produzione
KNeighborsRegressor(
algorithm = 'auto', leaf_size = 30, metric = 'minkowski',
metric_params = None, n_jobs = None, n_neighbors = 8, p = 2,
weights = 'uniform'
)Esempio
Ora possiamo trovare l'MSE (Mean Squared Error) come segue:
print ("The MSE is:",format(np.power(y-knnr.predict(X),4).mean()))Produzione
The MSE is: 4.4333349609375Esempio
Ora, usalo per prevedere il valore come segue:
X = [[0], [1], [2], [3]]
y = [0, 0, 1, 1]
from sklearn.neighbors import KNeighborsRegressor
knnr = KNeighborsRegressor(n_neighbors = 3)
knnr.fit(X, y)
print(knnr.predict([[2.5]]))Produzione
[0.66666667]Completo programma funzionante / eseguibile
from sklearn.datasets import load_iris
iris = load_iris()
X = iris.data[:, :4]
y = iris.target
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.20)
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(X_train)
X_train = scaler.transform(X_train)
X_test = scaler.transform(X_test)
import numpy as np
from sklearn.neighbors import KNeighborsRegressor
knnr = KNeighborsRegressor(n_neighbors=8)
knnr.fit(X_train, y_train)
print ("The MSE is:",format(np.power(y-knnr.predict(X),4).mean()))
X = [[0], [1], [2], [3]]
y = [0, 0, 1, 1]
from sklearn.neighbors import KNeighborsRegressor
knnr = KNeighborsRegressor(n_neighbors=3)
knnr.fit(X, y)
print(knnr.predict([[2.5]]))RadiusNeighborsRegressor
Il raggio nel nome di questo regressore rappresenta i vicini più vicini all'interno di un raggio specificato r, dove r è un valore a virgola mobile specificato dall'utente. Quindi, come suggerisce il nome, questo regressore implementa l'apprendimento in base al numero di vicini entro un raggio fisso r di ciascun punto di addestramento. Capiamolo di più con l'aiuto se un esempio di implementazione -
Esempio di implementazione
In questo esempio, implementeremo KNN sul set di dati denominato Iris Flower data set utilizzando scikit-learn RadiusNeighborsRegressor -
Innanzitutto, importa il set di dati dell'iride come segue:
from sklearn.datasets import load_iris
iris = load_iris()Ora, dobbiamo suddividere i dati in dati di addestramento e test. Useremo la funzione Sklearn train_test_split per dividere i dati nel rapporto di 70 (dati di addestramento) e 20 (dati di test) -
X = iris.data[:, :4]
y = iris.target
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.20)Successivamente, eseguiremo il ridimensionamento dei dati con l'aiuto del modulo di pre-elaborazione Sklearn come segue:
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(X_train)
X_train = scaler.transform(X_train)
X_test = scaler.transform(X_test)Quindi, importa il file RadiusneighborsRegressor classe da Sklearn e fornire il valore del raggio come segue:
import numpy as np
from sklearn.neighbors import RadiusNeighborsRegressor
knnr_r = RadiusNeighborsRegressor(radius=1)
knnr_r.fit(X_train, y_train)Esempio
Ora possiamo trovare l'MSE (Mean Squared Error) come segue:
print ("The MSE is:",format(np.power(y-knnr_r.predict(X),4).mean()))Produzione
The MSE is: The MSE is: 5.666666666666667Esempio
Ora, usalo per prevedere il valore come segue:
X = [[0], [1], [2], [3]]
y = [0, 0, 1, 1]
from sklearn.neighbors import RadiusNeighborsRegressor
knnr_r = RadiusNeighborsRegressor(radius=1)
knnr_r.fit(X, y)
print(knnr_r.predict([[2.5]]))Produzione
[1.]Completo programma funzionante / eseguibile
from sklearn.datasets import load_iris
iris = load_iris()
X = iris.data[:, :4]
y = iris.target
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.20)
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(X_train)
X_train = scaler.transform(X_train)
X_test = scaler.transform(X_test)
import numpy as np
from sklearn.neighbors import RadiusNeighborsRegressor
knnr_r = RadiusNeighborsRegressor(radius = 1)
knnr_r.fit(X_train, y_train)
print ("The MSE is:",format(np.power(y-knnr_r.predict(X),4).mean()))
X = [[0], [1], [2], [3]]
y = [0, 0, 1, 1]
from sklearn.neighbors import RadiusNeighborsRegressor
knnr_r = RadiusNeighborsRegressor(radius = 1)
knnr_r.fit(X, y)
print(knnr_r.predict([[2.5]]))I metodi Naïve Bayes sono un insieme di algoritmi di apprendimento supervisionato basati sull'applicazione del teorema di Bayes con una forte assunzione che tutti i predittori siano indipendenti l'uno dall'altro, cioè la presenza di una caratteristica in una classe è indipendente dalla presenza di qualsiasi altra caratteristica nella stessa classe. Questo è un presupposto ingenuo ed è per questo che questi metodi sono chiamati metodi Naïve Bayes.
Il teorema di Bayes afferma la seguente relazione per trovare la probabilità a posteriori di classe, cioè la probabilità di un'etichetta e alcune caratteristiche osservate, $P\left(\begin{array}{c} Y\arrowvert features\end{array}\right)$.
$$P\left(\begin{array}{c} Y\arrowvert features\end{array}\right)=\left(\frac{P\lgroup Y\rgroup P\left(\begin{array}{c} features\arrowvert Y\end{array}\right)}{P\left(\begin{array}{c} features\end{array}\right)}\right)$$Qui, $P\left(\begin{array}{c} Y\arrowvert features\end{array}\right)$ è la probabilità a posteriori di classe.
$P\left(\begin{array}{c} Y\end{array}\right)$ è la probabilità a priori della classe.
$P\left(\begin{array}{c} features\arrowvert Y\end{array}\right)$ è la probabilità che è la probabilità del predittore data la classe.
$P\left(\begin{array}{c} features\end{array}\right)$ è la probabilità a priori del predittore.
Lo Scikit-learn fornisce diversi modelli di classificatori bayesiani ingenui, vale a dire Gaussiano, Multinomiale, Complemento e Bernoulli. Tutti differiscono principalmente per l'assunzione che fanno riguardo alla distribuzione di$P\left(\begin{array}{c} features\arrowvert Y\end{array}\right)$ cioè la probabilità del predittore data la classe.
| Suor n | Descrizione del Modello |
|---|---|
| 1 | Gaussian Naïve Bayes Il classificatore gaussiano Naïve Bayes presume che i dati di ciascuna etichetta siano tratti da una semplice distribuzione gaussiana. |
| 2 | Naïve Bayes multinomiale Si presume che le caratteristiche siano tratte da una semplice distribuzione multinomiale. |
| 3 | Bernoulli Naïve Bayes Il presupposto in questo modello è che le caratteristiche binarie (0 e 1) in natura. Un'applicazione della classificazione Bernoulli Naïve Bayes è la classificazione del testo con il modello "borsa di parole" |
| 4 | Complemento Naïve Bayes È stato progettato per correggere le gravi ipotesi formulate dal classificatore multinomiale Bayes. Questo tipo di classificatore NB è adatto per set di dati sbilanciati |
Building Naïve Bayes Classifier
Possiamo anche applicare il classificatore Naïve Bayes al set di dati Scikit-learn. Nell'esempio seguente, stiamo applicando GaussianNB e adattando il set di dati breast_cancer di Scikit-leran.
Esempio
Import Sklearn
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
data = load_breast_cancer()
label_names = data['target_names']
labels = data['target']
feature_names = data['feature_names']
features = data['data']
print(label_names)
print(labels[0])
print(feature_names[0])
print(features[0])
train, test, train_labels, test_labels = train_test_split(
features,labels,test_size = 0.40, random_state = 42
)
from sklearn.naive_bayes import GaussianNB
GNBclf = GaussianNB()
model = GNBclf.fit(train, train_labels)
preds = GNBclf.predict(test)
print(preds)Produzione
[
1 0 0 1 1 0 0 0 1 1 1 0 1 0 1 0 1 1 1 0 1 1 0 1 1 1 1
1 1 0 1 1 1 1 1 1 0 1 0 1 1 0 1 1 1 1 1 1 1 1 0 0 1 1
1 1 1 0 0 1 1 0 0 1 1 1 0 0 1 1 0 0 1 0 1 1 1 1 1 1 0
1 1 0 0 0 0 0 1 1 1 1 1 1 1 1 0 0 1 0 0 1 0 0 1 1 1 0
1 1 0 1 1 0 0 0 1 1 1 0 0 1 1 0 1 0 0 1 1 0 0 0 1 1 1
0 1 1 0 0 1 0 1 1 0 1 0 0 1 1 1 1 1 1 1 0 0 1 1 1 1 1
1 1 1 1 1 1 1 0 1 1 1 0 1 1 0 1 1 1 1 1 1 0 0 0 1 1 0
1 0 1 1 1 1 0 1 1 0 1 1 1 0 1 0 0 1 1 1 1 1 1 1 1 0 1
1 1 1 1 0 1 0 0 1 1 0 1
]L'output di cui sopra consiste in una serie di 0 e 1 che sono fondamentalmente i valori previsti dalle classi tumorali, vale a dire maligni e benigni.
In questo capitolo impareremo il metodo di apprendimento in Sklearn, che viene definito albero decisionale.
Decisions tress (DTs) sono il metodo di apprendimento supervisionato non parametrico più potente. Possono essere utilizzati per le attività di classificazione e regressione. L'obiettivo principale dei DT è creare un modello che preveda il valore della variabile obiettivo apprendendo semplici regole decisionali dedotte dalle caratteristiche dei dati. Gli alberi decisionali hanno due entità principali; uno è il nodo radice, dove i dati si dividono, e l'altro è il nodo decisionale o se ne va, dove abbiamo ottenuto l'output finale.
Algoritmi dell'albero decisionale
Di seguito vengono spiegati diversi algoritmi dell'albero decisionale:
ID3
È stato sviluppato da Ross Quinlan nel 1986. È anche chiamato Iterative Dichotomiser 3. L'obiettivo principale di questo algoritmo è trovare quelle caratteristiche categoriali, per ogni nodo, che produrranno il maggior guadagno di informazioni per obiettivi categoriali.
Consente all'albero di crescere fino alle dimensioni massime e quindi, per migliorare la capacità dell'albero su dati invisibili, applica una fase di potatura. L'output di questo algoritmo sarebbe un albero a più vie.
C4.5
È il successore di ID3 e definisce dinamicamente un attributo discreto che divide il valore dell'attributo continuo in un insieme discreto di intervalli. Questo è il motivo per cui ha rimosso la restrizione delle caratteristiche categoriali. Converte l'albero addestrato ID3 in set di regole "IF-THEN".
Al fine di determinare la sequenza in cui queste regole dovrebbero essere applicate, l'accuratezza di ciascuna regola verrà valutata per prima.
C5.0
Funziona in modo simile a C4.5 ma utilizza meno memoria e crea regole più piccole. È più preciso di C4.5.
CARRELLO
Si chiama algoritmo di classificazione e regressione degli alberi. Fondamentalmente genera suddivisioni binarie utilizzando le caratteristiche e la soglia che producono il maggior guadagno di informazioni su ciascun nodo (chiamato indice di Gini).
L'omogeneità dipende dall'indice di Gini, maggiore è il valore dell'indice di Gini, maggiore sarebbe l'omogeneità. È come l'algoritmo C4.5, ma la differenza è che non calcola set di regole e non supporta anche variabili target numeriche (regressione).
Classificazione con alberi decisionali
In questo caso, le variabili decisionali sono categoriche.
Sklearn Module - La libreria Scikit-learn fornisce il nome del modulo DecisionTreeClassifier per eseguire la classificazione multiclasse sul set di dati.
Parametri
La tabella seguente è composta dai parametri utilizzati da sklearn.tree.DecisionTreeClassifier modulo -
| Suor n | Parametro e descrizione |
|---|---|
| 1 | criterion - stringa, valore predefinito opzionale = "gini" Rappresenta la funzione per misurare la qualità di uno split. I criteri supportati sono "gini" e "entropia". L'impostazione predefinita è gini che è per l'impurità di Gini mentre l'entropia è per il guadagno di informazioni. |
| 2 | splitter - stringa, impostazione predefinita opzionale = "migliore" Indica al modello quale strategia tra "migliore" o "casuale" scegliere la suddivisione in ciascun nodo. |
| 3 | max_depth - int o None, valore predefinito opzionale = None Questo parametro decide la profondità massima dell'albero. Il valore predefinito è Nessuno, il che significa che i nodi si espandono fino a quando tutte le foglie sono pure o finché tutte le foglie non contengono meno di min_smaples_split campioni. |
| 4 | min_samples_split - int, float, predefinito opzionale = 2 Questo parametro fornisce il numero minimo di campioni necessari per dividere un nodo interno. |
| 5 | min_samples_leaf - int, float, predefinito opzionale = 1 Questo parametro fornisce il numero minimo di campioni necessari per trovarsi in un nodo foglia. |
| 6 | min_weight_fraction_leaf - float, impostazione predefinita opzionale = 0. Con questo parametro, il modello otterrà la frazione ponderata minima della somma dei pesi richiesti per essere in un nodo foglia. |
| 7 | max_features - int, float, string o None, valore predefinito opzionale = None Fornisce al modello il numero di caratteristiche da considerare quando si cerca la divisione migliore. |
| 8 | random_state - int, istanza RandomState o None, opzionale, default = nessuno Questo parametro rappresenta il seme del numero pseudo casuale generato che viene utilizzato durante la mescolanza dei dati. Le seguenti sono le opzioni:
|
| 9 | max_leaf_nodes - int o None, valore predefinito opzionale = None Questo parametro farà crescere un albero con max_leaf_nodes nel modo migliore per primo. L'impostazione predefinita è nessuno, il che significa che ci sarebbe un numero illimitato di nodi foglia. |
| 10 | min_impurity_decrease - float, impostazione predefinita opzionale = 0. Questo valore funziona come criterio per la divisione di un nodo perché il modello dividerà un nodo se questa divisione induce una diminuzione dell'impurità maggiore o uguale a min_impurity_decrease value. |
| 11 | min_impurity_split - float, predefinito = 1e-7 Rappresenta la soglia per l'arresto anticipato della crescita degli alberi. |
| 12 | class_weight - dict, elenco di dict, "bilanciato" o Nessuno, impostazione predefinita = Nessuno Rappresenta i pesi associati alle classi. La forma è {class_label: weight}. Se usiamo l'opzione predefinita, significa che tutte le classi dovrebbero avere un peso. D'altra parte, se scegliclass_weight: balanced, utilizzerà i valori di y per regolare automaticamente i pesi. |
| 13 | presort - bool, valore predefinito opzionale = False Indica al modello se presortare i dati per accelerare la ricerca delle migliori suddivisioni nell'adattamento. L'impostazione predefinita è false ma se impostata su true, potrebbe rallentare il processo di addestramento. |
Attributi
La tabella seguente è costituita dagli attributi utilizzati da sklearn.tree.DecisionTreeClassifier modulo -
| Suor n | Parametro e descrizione |
|---|---|
| 1 | feature_importances_ - matrice di forma = [n_features] Questo attributo restituirà l'importanza della caratteristica. |
| 2 | classes_: - array di shape = [n_classes] o un elenco di tali array Rappresenta le etichette delle classi, ovvero il problema dell'uscita singola, o un elenco di array di etichette delle classi, ovvero il problema dell'uscita multipla. |
| 3 | max_features_ - int Rappresenta il valore dedotto del parametro max_features. |
| 4 | n_classes_ - int o elenco Rappresenta il numero di classi, ovvero il problema con un singolo output, o un elenco di numero di classi per ogni output, ovvero il problema con più output. |
| 5 | n_features_ - int Fornisce il numero di features quando viene eseguito il metodo fit (). |
| 6 | n_outputs_ - int Fornisce il numero di outputs quando viene eseguito il metodo fit (). |
Metodi
La tabella seguente comprende i metodi utilizzati da sklearn.tree.DecisionTreeClassifier modulo -
| Suor n | Parametro e descrizione |
|---|---|
| 1 | apply(self, X [, check_input]) Questo metodo restituirà l'indice della foglia. |
| 2 | decision_path(self, X [, check_input]) Come suggerisce il nome, questo metodo restituirà il percorso decisionale nell'albero |
| 3 | fit(self, X, y [, sample_weight, ...]) Il metodo fit () costruirà un classificatore dell'albero decisionale da un dato set di addestramento (X, y). |
| 4 | get_depth(se stesso) Come suggerisce il nome, questo metodo restituirà la profondità dell'albero decisionale |
| 5 | get_n_leaves(se stesso) Come suggerisce il nome, questo metodo restituirà il numero di foglie dell'albero decisionale. |
| 6 | get_params(self [, deep]) Possiamo usare questo metodo per ottenere i parametri per lo stimatore. |
| 7 | predict(self, X [, check_input]) Prevede il valore della classe per X. |
| 8 | predict_log_proba(sé, X) Prevede le probabilità di log di classe dei campioni di input forniti da noi, X. |
| 9 | predict_proba(self, X [, check_input]) Prevede le probabilità di classe dei campioni di input forniti da noi, X. |
| 10 | score(self, X, y [, sample_weight]) Come suggerisce il nome, il metodo score () restituirà la precisione media sui dati e le etichette del test forniti. |
| 11 | set_params(self, \ * \ * params) Possiamo impostare i parametri dello stimatore con questo metodo. |
Esempio di implementazione
Lo script Python di seguito utilizzerà sklearn.tree.DecisionTreeClassifier modulo per costruire un classificatore per prevedere maschi o femmine dal nostro set di dati con 25 campioni e due caratteristiche, ovvero 'altezza' e 'lunghezza dei capelli' -
from sklearn import tree
from sklearn.model_selection import train_test_split
X=[[165,19],[175,32],[136,35],[174,65],[141,28],[176,15]
,[131,32],[166,6],[128,32],[179,10],[136,34],[186,2],[12
6,25],[176,28],[112,38],[169,9],[171,36],[116,25],[196,2
5], [196,38], [126,40], [197,20], [150,25], [140,32],[136,35]]
Y=['Man','Woman','Woman','Man','Woman','Man','Woman','Ma
n','Woman','Man','Woman','Man','Woman','Woman','Woman','
Man','Woman','Woman','Man', 'Woman', 'Woman', 'Man', 'Man', 'Woman', 'Woman']
data_feature_names = ['height','length of hair']
X_train, X_test, y_train, y_test = train_test_split(X, Y, test_size = 0.3, random_state = 1)
DTclf = tree.DecisionTreeClassifier()
DTclf = clf.fit(X,Y)
prediction = DTclf.predict([[135,29]])
print(prediction)Produzione
['Woman']Possiamo anche prevedere la probabilità di ogni classe utilizzando il seguente metodo python prediction_proba () come segue:
Esempio
prediction = DTclf.predict_proba([[135,29]])
print(prediction)Produzione
[[0. 1.]]Regressione con alberi decisionali
In questo caso le variabili decisionali sono continue.
Sklearn Module - La libreria Scikit-learn fornisce il nome del modulo DecisionTreeRegressor per applicare alberi decisionali su problemi di regressione.
Parametri
Parametri utilizzati da DecisionTreeRegressor sono quasi uguali a quelli usati in DecisionTreeClassifiermodulo. La differenza sta nel parametro "criterio". PerDecisionTreeRegressor moduli ‘criterion: string, optional default = "mse" 'parametri hanno i seguenti valori -
mse- Sta per errore quadratico medio. È uguale alla riduzione della varianza come criterio di selezione delle caratteristiche. Riduce al minimo la perdita di L2 utilizzando la media di ciascun nodo terminale.
freidman_mse - Utilizza anche l'errore quadratico medio ma con il punteggio di miglioramento di Friedman.
mae- Sta per l'errore medio assoluto. Riduce al minimo la perdita L1 utilizzando la mediana di ciascun nodo terminale.
Un'altra differenza è che non ha ‘class_weight’ parametro.
Attributi
Attributi di DecisionTreeRegressor sono uguali a quelle di DecisionTreeClassifiermodulo. La differenza è che non ce l'ha‘classes_’ e ‘n_classes_attributi.
Metodi
Metodi di DecisionTreeRegressor sono uguali a quelle di DecisionTreeClassifiermodulo. La differenza è che non ce l'ha‘predict_log_proba()’ e ‘predict_proba()’attributi.
Esempio di implementazione
Il metodo fit () nel modello di regressione dell'albero decisionale assumerà valori in virgola mobile di y. vediamo un semplice esempio di implementazione utilizzandoSklearn.tree.DecisionTreeRegressor -
from sklearn import tree
X = [[1, 1], [5, 5]]
y = [0.1, 1.5]
DTreg = tree.DecisionTreeRegressor()
DTreg = clf.fit(X, y)Una volta adattato, possiamo utilizzare questo modello di regressione per fare previsioni come segue:
DTreg.predict([[4, 5]])Produzione
array([1.5])Questo capitolo ti aiuterà a comprendere gli alberi decisionali casuali in Sklearn.
Algoritmi di albero decisionale randomizzato
Poiché sappiamo che un DT viene solitamente addestrato suddividendo in modo ricorsivo i dati, ma essendo inclini all'overfit, sono stati trasformati in foreste casuali addestrando molti alberi su vari sottocampioni di dati. Ilsklearn.ensemble il modulo sta avendo i seguenti due algoritmi basati su alberi decisionali randomizzati:
L'algoritmo Random Forest
Per ogni caratteristica in esame, calcola la combinazione caratteristica / suddivisione ottimale a livello locale. Nella foresta casuale, ogni albero decisionale nell'insieme è costruito da un campione estratto con sostituzione dal set di addestramento e quindi ottiene la previsione da ciascuno di essi e infine seleziona la soluzione migliore mediante il voto. Può essere utilizzato sia per la classificazione che per le attività di regressione.
Classificazione con Random Forest
Per creare un classificatore di foresta casuale, il modulo Scikit-learn fornisce sklearn.ensemble.RandomForestClassifier. Durante la creazione di classificatori di foreste casuali, i parametri principali utilizzati da questo modulo sono‘max_features’ e ‘n_estimators’.
Qui, ‘max_features’è la dimensione dei sottoinsiemi casuali di funzionalità da considerare quando si divide un nodo. Se scegliamo il valore di questo parametro su nessuno, considererà tutte le caratteristiche piuttosto che un sottoinsieme casuale. D'altra parte,n_estimatorssono il numero di alberi nella foresta. Maggiore è il numero di alberi, migliore sarà il risultato. Ma ci vorrà anche più tempo per calcolare.
Esempio di implementazione
Nell'esempio seguente, stiamo creando un classificatore di foresta casuale utilizzando sklearn.ensemble.RandomForestClassifier e verificandone l'accuratezza anche utilizzando cross_val_score modulo.
from sklearn.model_selection import cross_val_score
from sklearn.datasets import make_blobs
from sklearn.ensemble import RandomForestClassifier
X, y = make_blobs(n_samples = 10000, n_features = 10, centers = 100,random_state = 0) RFclf = RandomForestClassifier(n_estimators = 10,max_depth = None,min_samples_split = 2, random_state = 0)
scores = cross_val_score(RFclf, X, y, cv = 5)
scores.mean()Produzione
0.9997Esempio
Possiamo anche utilizzare il set di dati sklearn per creare un classificatore di foresta casuale. Come nell'esempio seguente, stiamo usando il set di dati iris. Troveremo anche il suo punteggio di accuratezza e la matrice di confusione.
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import classification_report, confusion_matrix, accuracy_score
path = "https://archive.ics.uci.edu/ml/machine-learning-database
s/iris/iris.data"
headernames = ['sepal-length', 'sepal-width', 'petal-length', 'petal-width', 'Class']
dataset = pd.read_csv(path, names = headernames)
X = dataset.iloc[:, :-1].values
y = dataset.iloc[:, 4].values
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.30)
RFclf = RandomForestClassifier(n_estimators = 50)
RFclf.fit(X_train, y_train)
y_pred = RFclf.predict(X_test)
result = confusion_matrix(y_test, y_pred)
print("Confusion Matrix:")
print(result)
result1 = classification_report(y_test, y_pred)
print("Classification Report:",)
print (result1)
result2 = accuracy_score(y_test,y_pred)
print("Accuracy:",result2)Produzione
Confusion Matrix:
[[14 0 0]
[ 0 18 1]
[ 0 0 12]]
Classification Report:
precision recall f1-score support
Iris-setosa 1.00 1.00 1.00 14
Iris-versicolor 1.00 0.95 0.97 19
Iris-virginica 0.92 1.00 0.96 12
micro avg 0.98 0.98 0.98 45
macro avg 0.97 0.98 0.98 45
weighted avg 0.98 0.98 0.98 45
Accuracy: 0.9777777777777777Regressione con foresta casuale
Per creare una regressione della foresta casuale, il modulo Scikit-learn fornisce sklearn.ensemble.RandomForestRegressor. Durante la creazione di un regressore forestale casuale, utilizzerà gli stessi parametri utilizzati dasklearn.ensemble.RandomForestClassifier.
Esempio di implementazione
Nell'esempio seguente, stiamo costruendo un regressore di foresta casuale utilizzando sklearn.ensemble.RandomForestregressor e anche prevedere nuovi valori utilizzando il metodo prediction ().
from sklearn.ensemble import RandomForestRegressor
from sklearn.datasets import make_regression
X, y = make_regression(n_features = 10, n_informative = 2,random_state = 0, shuffle = False)
RFregr = RandomForestRegressor(max_depth = 10,random_state = 0,n_estimators = 100)
RFregr.fit(X, y)Produzione
RandomForestRegressor(
bootstrap = True, criterion = 'mse', max_depth = 10,
max_features = 'auto', max_leaf_nodes = None,
min_impurity_decrease = 0.0, min_impurity_split = None,
min_samples_leaf = 1, min_samples_split = 2,
min_weight_fraction_leaf = 0.0, n_estimators = 100, n_jobs = None,
oob_score = False, random_state = 0, verbose = 0, warm_start = False
)Una volta adattato, possiamo prevedere dal modello di regressione come segue:
print(RFregr.predict([[0, 2, 3, 0, 1, 1, 1, 1, 2, 2]]))Produzione
[98.47729198]Metodi extra-albero
Per ogni caratteristica in esame, seleziona un valore casuale per la divisione. Il vantaggio di utilizzare metodi albero aggiuntivi è che consente di ridurre un po 'di più la varianza del modello. Lo svantaggio dell'utilizzo di questi metodi è che aumenta leggermente il bias.
Classificazione con metodo Extra-Tree
Per creare un classificatore utilizzando il metodo Extra-tree, il modulo Scikit-learn fornisce sklearn.ensemble.ExtraTreesClassifier. Utilizza gli stessi parametri utilizzati dasklearn.ensemble.RandomForestClassifier. L'unica differenza è nel modo in cui, discusso sopra, costruiscono gli alberi.
Esempio di implementazione
Nell'esempio seguente, stiamo creando un classificatore di foresta casuale utilizzando sklearn.ensemble.ExtraTreeClassifier e anche verificandone l'accuratezza utilizzando cross_val_score modulo.
from sklearn.model_selection import cross_val_score
from sklearn.datasets import make_blobs
from sklearn.ensemble import ExtraTreesClassifier
X, y = make_blobs(n_samples = 10000, n_features = 10, centers=100,random_state = 0)
ETclf = ExtraTreesClassifier(n_estimators = 10,max_depth = None,min_samples_split = 10, random_state = 0)
scores = cross_val_score(ETclf, X, y, cv = 5)
scores.mean()Produzione
1.0Esempio
Possiamo anche utilizzare il set di dati sklearn per creare un classificatore utilizzando il metodo Extra-Tree. Come nell'esempio seguente, stiamo utilizzando il set di dati Pima-Indian.
from pandas import read_csv
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.ensemble import ExtraTreesClassifier
path = r"C:\pima-indians-diabetes.csv"
headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=headernames)
array = data.values
X = array[:,0:8]
Y = array[:,8]
seed = 7
kfold = KFold(n_splits=10, random_state=seed)
num_trees = 150
max_features = 5
ETclf = ExtraTreesClassifier(n_estimators=num_trees, max_features=max_features)
results = cross_val_score(ETclf, X, Y, cv=kfold)
print(results.mean())Produzione
0.7551435406698566Regressione con metodo Extra-Tree
Per creare un file Extra-Tree regressione, fornisce il modulo Scikit-learn sklearn.ensemble.ExtraTreesRegressor. Durante la creazione di un regressore forestale casuale, utilizzerà gli stessi parametri utilizzati dasklearn.ensemble.ExtraTreesClassifier.
Esempio di implementazione
Nell'esempio seguente, stiamo applicando sklearn.ensemble.ExtraTreesregressore sugli stessi dati che abbiamo usato durante la creazione di un regressore forestale casuale. Vediamo la differenza nell'output
from sklearn.ensemble import ExtraTreesRegressor
from sklearn.datasets import make_regression
X, y = make_regression(n_features = 10, n_informative = 2,random_state = 0, shuffle = False)
ETregr = ExtraTreesRegressor(max_depth = 10,random_state = 0,n_estimators = 100)
ETregr.fit(X, y)Produzione
ExtraTreesRegressor(bootstrap = False, criterion = 'mse', max_depth = 10,
max_features = 'auto', max_leaf_nodes = None,
min_impurity_decrease = 0.0, min_impurity_split = None,
min_samples_leaf = 1, min_samples_split = 2,
min_weight_fraction_leaf = 0.0, n_estimators = 100, n_jobs = None,
oob_score = False, random_state = 0, verbose = 0, warm_start = False)Esempio
Una volta adattato, possiamo prevedere dal modello di regressione come segue:
print(ETregr.predict([[0, 2, 3, 0, 1, 1, 1, 1, 2, 2]]))Produzione
[85.50955817]In questo capitolo, impareremo i metodi di potenziamento in Sklearn, che consente di costruire un modello di insieme.
I metodi di potenziamento creano un modello di insieme in modo incrementale. Il principio principale è costruire il modello in modo incrementale addestrando ogni stimatore del modello di base in modo sequenziale. Per creare un insieme potente, questi metodi fondamentalmente combinano studenti di diverse settimane che vengono addestrati in sequenza su più iterazioni di dati di formazione. Il modulo sklearn.ensemble ha i seguenti due metodi di potenziamento.
AdaBoost
È uno dei metodi di potenziamento dell'insieme di maggior successo la cui chiave principale è nel modo in cui danno peso alle istanze nel set di dati. Ecco perché l'algoritmo deve prestare meno attenzione alle istanze durante la costruzione dei modelli successivi.
Classificazione con AdaBoost
Per creare un classificatore AdaBoost, il modulo Scikit-learn fornisce sklearn.ensemble.AdaBoostClassifier. Durante la creazione di questo classificatore, il parametro principale utilizzato da questo modulo èbase_estimator. In questo caso, base_estimator è il valore dibase estimatorda cui è costruito l'ensemble potenziato. Se scegliamo il valore di questo parametro su nessuno, lo stimatore di base sarebbeDecisionTreeClassifier(max_depth=1).
Esempio di implementazione
Nel seguente esempio, stiamo costruendo un classificatore AdaBoost utilizzando sklearn.ensemble.AdaBoostClassifier e anche prevedere e controllare il suo punteggio.
from sklearn.ensemble import AdaBoostClassifier
from sklearn.datasets import make_classification
X, y = make_classification(n_samples = 1000, n_features = 10,n_informative = 2, n_redundant = 0,random_state = 0, shuffle = False)
ADBclf = AdaBoostClassifier(n_estimators = 100, random_state = 0)
ADBclf.fit(X, y)Produzione
AdaBoostClassifier(algorithm = 'SAMME.R', base_estimator = None,
learning_rate = 1.0, n_estimators = 100, random_state = 0)Esempio
Una volta adattati, possiamo prevedere nuovi valori come segue:
print(ADBclf.predict([[0, 2, 3, 0, 1, 1, 1, 1, 2, 2]]))Produzione
[1]Esempio
Ora possiamo controllare il punteggio come segue:
ADBclf.score(X, y)Produzione
0.995Esempio
Possiamo anche utilizzare il set di dati sklearn per creare un classificatore utilizzando il metodo Extra-Tree. Ad esempio, in un esempio fornito di seguito, stiamo utilizzando il set di dati Pima-Indian.
from pandas import read_csv
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.ensemble import AdaBoostClassifier
path = r"C:\pima-indians-diabetes.csv"
headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names = headernames)
array = data.values
X = array[:,0:8]
Y = array[:,8]
seed = 5
kfold = KFold(n_splits = 10, random_state = seed)
num_trees = 100
max_features = 5
ADBclf = AdaBoostClassifier(n_estimators = num_trees, max_features = max_features)
results = cross_val_score(ADBclf, X, Y, cv = kfold)
print(results.mean())Produzione
0.7851435406698566Regressione con AdaBoost
Per creare un regressore con il metodo Ada Boost, la libreria Scikit-learn fornisce sklearn.ensemble.AdaBoostRegressor. Durante la creazione di regressore, utilizzerà gli stessi parametri utilizzati dasklearn.ensemble.AdaBoostClassifier.
Esempio di implementazione
Nell'esempio seguente, stiamo costruendo un regressore AdaBoost utilizzando sklearn.ensemble.AdaBoostregressor e anche prevedere nuovi valori utilizzando il metodo prediction ().
from sklearn.ensemble import AdaBoostRegressor
from sklearn.datasets import make_regression
X, y = make_regression(n_features = 10, n_informative = 2,random_state = 0, shuffle = False)
ADBregr = RandomForestRegressor(random_state = 0,n_estimators = 100)
ADBregr.fit(X, y)Produzione
AdaBoostRegressor(base_estimator = None, learning_rate = 1.0, loss = 'linear',
n_estimators = 100, random_state = 0)Esempio
Una volta adattato, possiamo prevedere dal modello di regressione come segue:
print(ADBregr.predict([[0, 2, 3, 0, 1, 1, 1, 1, 2, 2]]))Produzione
[85.50955817]Aumento gradiente dell'albero
È anche chiamato Gradient Boosted Regression Trees(GRBT). È fondamentalmente una generalizzazione del potenziamento a funzioni di perdita differenziabili arbitrarie. Produce un modello di previsione sotto forma di un insieme di modelli di previsione settimanali. Può essere utilizzato per i problemi di regressione e classificazione. Il loro vantaggio principale risiede nel fatto che gestiscono naturalmente i dati di tipo misto.
Classificazione con Gradient Tree Boost
Per creare un classificatore Gradient Tree Boost, il modulo Scikit-learn fornisce sklearn.ensemble.GradientBoostingClassifier. Durante la creazione di questo classificatore, il parametro principale utilizzato da questo modulo è "perdita". In questo caso, "perdita" è il valore della funzione di perdita da ottimizzare. Se scegliamo perdita = devianza, ci si riferisce alla devianza per la classificazione con output probabilistici.
D'altra parte, se scegliamo il valore di questo parametro su esponenziale, ripristina l'algoritmo AdaBoost. Il parametron_estimatorscontrollerà il numero di studenti settimanali. Un iperparametro denominatolearning_rate (nell'intervallo di (0,0, 1,0]) controllerà l'overfitting tramite restringimento.
Esempio di implementazione
Nell'esempio seguente, stiamo creando un classificatore di incremento gradiente utilizzando sklearn.ensemble.GradientBoostingClassifier. Stiamo adattando questo classificatore a studenti di 50 settimane.
from sklearn.datasets import make_hastie_10_2
from sklearn.ensemble import GradientBoostingClassifier
X, y = make_hastie_10_2(random_state = 0)
X_train, X_test = X[:5000], X[5000:]
y_train, y_test = y[:5000], y[5000:]
GDBclf = GradientBoostingClassifier(n_estimators = 50, learning_rate = 1.0,max_depth = 1, random_state = 0).fit(X_train, y_train)
GDBclf.score(X_test, y_test)Produzione
0.8724285714285714Esempio
Possiamo anche utilizzare il set di dati sklearn per creare un classificatore utilizzando Gradient Boosting Classifier. Come nell'esempio seguente, stiamo utilizzando il set di dati Pima-Indian.
from pandas import read_csv
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.ensemble import GradientBoostingClassifier
path = r"C:\pima-indians-diabetes.csv"
headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names = headernames)
array = data.values
X = array[:,0:8]
Y = array[:,8]
seed = 5
kfold = KFold(n_splits = 10, random_state = seed)
num_trees = 100
max_features = 5
ADBclf = GradientBoostingClassifier(n_estimators = num_trees, max_features = max_features)
results = cross_val_score(ADBclf, X, Y, cv = kfold)
print(results.mean())Produzione
0.7946582356674234Regressione con aumento gradiente dell'albero
Per creare un regressore con il metodo Gradient Tree Boost, la libreria Scikit-learn fornisce sklearn.ensemble.GradientBoostingRegressor. Può specificare la funzione di perdita per la regressione tramite la perdita del nome del parametro. Il valore predefinito per la perdita è "ls".
Esempio di implementazione
Nell'esempio seguente, stiamo costruendo un regressore con incremento gradiente utilizzando sklearn.ensemble.GradientBoostingregressor e anche trovare l'errore quadratico medio utilizzando il metodo mean_squared_error ().
import numpy as np
from sklearn.metrics import mean_squared_error
from sklearn.datasets import make_friedman1
from sklearn.ensemble import GradientBoostingRegressor
X, y = make_friedman1(n_samples = 2000, random_state = 0, noise = 1.0)
X_train, X_test = X[:1000], X[1000:]
y_train, y_test = y[:1000], y[1000:]
GDBreg = GradientBoostingRegressor(n_estimators = 80, learning_rate=0.1,
max_depth = 1, random_state = 0, loss = 'ls').fit(X_train, y_train)Una volta adattato, possiamo trovare l'errore quadratico medio come segue:
mean_squared_error(y_test, GDBreg.predict(X_test))Produzione
5.391246106657164Qui studieremo i metodi di clustering in Sklearn che aiuteranno nell'identificazione di qualsiasi somiglianza nei campioni di dati.
Metodi di clustering, uno dei metodi ML non supervisionati più utili, utilizzati per trovare modelli di somiglianza e relazione tra campioni di dati. Successivamente, raggruppano questi campioni in gruppi che hanno somiglianze in base alle caratteristiche. Il clustering determina il raggruppamento intrinseco tra i dati presenti senza etichetta, ecco perché è importante.
La libreria Scikit-learn ha sklearn.clusterper eseguire il raggruppamento di dati senza etichetta. Sotto questo modulo scikit-leran ha i seguenti metodi di clustering:
KMeans
Questo algoritmo calcola i centroidi e itera finché non trova il centroide ottimale. È necessario specificare il numero di cluster, motivo per cui si presume che siano già noti. La logica principale di questo algoritmo consiste nel raggruppare i dati che separano i campioni in un numero n di gruppi di uguali varianze riducendo al minimo i criteri noti come inerzia. Il numero di cluster identificati dall'algoritmo è rappresentato da "K.
Scikit-learn ha sklearn.cluster.KMeansmodulo per eseguire il clustering K-Means. Durante il calcolo dei centri dei cluster e del valore dell'inerzia, il parametro denominatosample_weight permette sklearn.cluster.KMeans modulo per assegnare più peso ad alcuni campioni.
Propagazione di affinità
Questo algoritmo si basa sul concetto di "passaggio di messaggi" tra diverse coppie di campioni fino alla convergenza. Non è necessario specificare il numero di cluster prima di eseguire l'algoritmo. L'algoritmo ha una complessità temporale dell'ordine (2), che è il più grande svantaggio di esso.
Scikit-learn ha sklearn.cluster.AffinityPropagation modulo per eseguire Affinity Propagation clustering.
Mean Shift
Questo algoritmo scopre principalmente blobsin una densità uniforme di campioni. Assegna iterativamente i punti dati ai cluster spostando i punti verso la densità di punti dati più alta. Invece di fare affidamento su un parametro denominatobandwidth determinando la dimensione della regione in cui cercare, imposta automaticamente il numero di cluster.
Scikit-learn ha sklearn.cluster.MeanShift modulo per eseguire il clustering Mean Shift.
Clustering spettrale
Prima del clustering, questo algoritmo utilizza fondamentalmente gli autovalori, ovvero lo spettro della matrice di similarità dei dati, per eseguire la riduzione della dimensionalità in un numero inferiore di dimensioni. L'utilizzo di questo algoritmo non è consigliabile in presenza di un numero elevato di cluster.
Scikit-learn ha sklearn.cluster.SpectralClustering modulo per eseguire il clustering spettrale.
Clustering gerarchico
Questo algoritmo crea cluster nidificati unendo o dividendo i cluster in successione. Questa gerarchia di cluster è rappresentata come un dendrogramma cioè un albero. Rientra nelle seguenti due categorie:
Agglomerative hierarchical algorithms- In questo tipo di algoritmo gerarchico, ogni punto dati viene trattato come un singolo cluster. Successivamente agglomerano le coppie di cluster. Questo utilizza l'approccio dal basso verso l'alto.
Divisive hierarchical algorithms- In questo algoritmo gerarchico, tutti i punti dati vengono trattati come un unico grande cluster. In questo il processo di clustering implica la divisione, utilizzando l'approccio top-down, l'unico grande cluster in vari piccoli cluster.
Scikit-learn ha sklearn.cluster.AgglomerativeClustering modulo per eseguire clustering gerarchico agglomerativo.
DBSCAN
Sta per “Density-based spatial clustering of applications with noise”. Questo algoritmo si basa sulla nozione intuitiva di "cluster" e "rumore" secondo cui i cluster sono regioni dense di densità inferiore nello spazio dati, separate da regioni a densità inferiore di punti dati.
Scikit-learn ha sklearn.cluster.DBSCANmodulo per eseguire il clustering DBSCAN. Ci sono due parametri importanti e cioè min_samples ed eps usati da questo algoritmo per definire denso.
Valore del parametro più alto min_samples o un valore più basso del parametro eps fornirà un'indicazione sulla maggiore densità di punti dati necessaria per formare un cluster.
OTTICA
Sta per “Ordering points to identify the clustering structure”. Questo algoritmo trova anche cluster basati sulla densità nei dati spaziali. La sua logica di funzionamento di base è come DBSCAN.
Affronta una delle principali debolezze dell'algoritmo DBSCAN, il problema di rilevare cluster significativi in dati di densità variabile, ordinando i punti del database in modo tale che i punti spazialmente più vicini diventino vicini nell'ordinamento.
Scikit-learn ha sklearn.cluster.OPTICS modulo per eseguire il clustering OTTICO.
BETULLA
È l'acronimo di riduzione iterativa bilanciata e raggruppamento mediante gerarchie. Viene utilizzato per eseguire il clustering gerarchico su set di dati di grandi dimensioni. Costruisce un albero denominatoCFT cioè Characteristics Feature Tree, per i dati forniti.
Il vantaggio di CFT è che i nodi di dati chiamati nodi CF (Characteristics Feature) contengono le informazioni necessarie per il clustering, il che impedisce ulteriormente la necessità di conservare in memoria tutti i dati di input.
Scikit-learn ha sklearn.cluster.Birch modulo per eseguire il clustering BETULLA.
Confronto tra algoritmi di clustering
La tabella seguente fornirà un confronto (basato su parametri, scalabilità e metrica) degli algoritmi di clustering in scikit-learn.
| Suor n | Nome algoritmo | Parametri | Scalabilità | Metrica utilizzata |
|---|---|---|---|---|
| 1 | K-Means | No. di cluster | N_samples molto grandi | La distanza tra i punti. |
| 2 | Propagazione di affinità | Smorzamento | Non è scalabile con n_samples | Distanza del grafico |
| 3 | Mean-Shift | Larghezza di banda | Non è scalabile con n_samples. | La distanza tra i punti. |
| 4 | Clustering spettrale | Numero di cluster | Livello medio di scalabilità con n_samples. Basso livello di scalabilità con n_clusters. | Distanza del grafico |
| 5 | Clustering gerarchico | Soglia di distanza o numero di cluster | Large n_samples Large n_clusters | La distanza tra i punti. |
| 6 | DBSCAN | Dimensioni del quartiere | N_samples molto grandi e n_clusters medi. | Distanza dal punto più vicino |
| 7 | OTTICA | Appartenenza minima al cluster | N_samples molto grandi e n_clusters di grandi dimensioni. | La distanza tra i punti. |
| 8 | BETULLA | Soglia, fattore di ramificazione | Large n_samples Large n_clusters | La distanza euclidea tra i punti. |
K-Means Clustering su Scikit-learn Digit dataset
In questo esempio, applicheremo il clustering K-means sul set di dati delle cifre. Questo algoritmo identificherà cifre simili senza utilizzare le informazioni sull'etichetta originale. L'implementazione viene eseguita sul notebook Jupyter.
%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()
import numpy as np
from sklearn.cluster import KMeans
from sklearn.datasets import load_digits
digits = load_digits()
digits.data.shapeProduzione
1797, 64)Questo output mostra che il set di dati digit contiene 1797 campioni con 64 funzioni.
Esempio
Ora, esegui il raggruppamento K-Means come segue:
kmeans = KMeans(n_clusters = 10, random_state = 0)
clusters = kmeans.fit_predict(digits.data)
kmeans.cluster_centers_.shapeProduzione
(10, 64)Questo output mostra che il clustering K-means ha creato 10 cluster con 64 funzionalità.
Esempio
fig, ax = plt.subplots(2, 5, figsize = (8, 3))
centers = kmeans.cluster_centers_.reshape(10, 8, 8)
for axi, center in zip(ax.flat, centers):
axi.set(xticks = [], yticks = [])
axi.imshow(center, interpolation = 'nearest', cmap = plt.cm.binary)Produzione
L'output seguente ha immagini che mostrano i centri dei cluster appresi da K-Means Clustering.

Successivamente, lo script Python di seguito abbinerà le etichette del cluster apprese (con K-Means) con le vere etichette trovate in esse -
from scipy.stats import mode
labels = np.zeros_like(clusters)
for i in range(10):
mask = (clusters == i)
labels[mask] = mode(digits.target[mask])[0]Possiamo anche verificare l'accuratezza con l'aiuto del comando indicato di seguito.
from sklearn.metrics import accuracy_score
accuracy_score(digits.target, labels)Produzione
0.7935447968836951Esempio di implementazione completo
%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()
import numpy as np
from sklearn.cluster import KMeans
from sklearn.datasets import load_digits
digits = load_digits()
digits.data.shape
kmeans = KMeans(n_clusters = 10, random_state = 0)
clusters = kmeans.fit_predict(digits.data)
kmeans.cluster_centers_.shape
fig, ax = plt.subplots(2, 5, figsize = (8, 3))
centers = kmeans.cluster_centers_.reshape(10, 8, 8)
for axi, center in zip(ax.flat, centers):
axi.set(xticks=[], yticks = [])
axi.imshow(center, interpolation = 'nearest', cmap = plt.cm.binary)
from scipy.stats import mode
labels = np.zeros_like(clusters)
for i in range(10):
mask = (clusters == i)
labels[mask] = mode(digits.target[mask])[0]
from sklearn.metrics import accuracy_score
accuracy_score(digits.target, labels)Esistono varie funzioni con l'aiuto delle quali possiamo valutare le prestazioni degli algoritmi di clustering.
Di seguito sono riportate alcune funzioni importanti e maggiormente utilizzate fornite da Scikit-learn per la valutazione delle prestazioni del clustering:
Indice Rand rettificato
Rand Index è una funzione che calcola una misura di somiglianza tra due raggruppamenti. Per questo calcolo, l'indice rand considera tutte le coppie di campioni e le coppie di conteggio assegnate nei cluster simili o diversi nel clustering previsto e vero. Successivamente, il punteggio dell'indice Rand grezzo viene `` aggiustato per caso '' nel punteggio dell'Indice Rand rettificato utilizzando la seguente formula:
$$Adjusted\:RI=\left(RI-Expected_{-}RI\right)/\left(max\left(RI\right)-Expected_{-}RI\right)$$Ha due parametri vale a dire labels_true, che è etichette di classe di verità di base, e labels_pred, che sono etichette di cluster da valutare.
Esempio
from sklearn.metrics.cluster import adjusted_rand_score
labels_true = [0, 0, 1, 1, 1, 1]
labels_pred = [0, 0, 2, 2, 3, 3]
adjusted_rand_score(labels_true, labels_pred)Produzione
0.4444444444444445Un'etichettatura perfetta avrebbe un punteggio 1 e un'etichettatura errata o un'etichettatura indipendente avrà un punteggio 0 o negativo.
Punteggio basato sulle informazioni reciproche
L'informazione reciproca è una funzione che calcola l'accordo dei due incarichi. Ignora le permutazioni. Sono disponibili le seguenti versioni:
Informazioni reciproche normalizzate (NMI)
Scikit impara ad avere sklearn.metrics.normalized_mutual_info_score modulo.
Esempio
from sklearn.metrics.cluster import normalized_mutual_info_score
labels_true = [0, 0, 1, 1, 1, 1]
labels_pred = [0, 0, 2, 2, 3, 3]
normalized_mutual_info_score (labels_true, labels_pred)Produzione
0.7611702597222881Informazioni reciproche modificate (AMI)
Scikit impara ad avere sklearn.metrics.adjusted_mutual_info_score modulo.
Esempio
from sklearn.metrics.cluster import adjusted_mutual_info_score
labels_true = [0, 0, 1, 1, 1, 1]
labels_pred = [0, 0, 2, 2, 3, 3]
adjusted_mutual_info_score (labels_true, labels_pred)Produzione
0.4444444444444448Punteggio Fowlkes-Mallows
La funzione Fowlkes-Mallows misura la somiglianza di due raggruppamenti di un insieme di punti. Può essere definita come la media geometrica della precisione e del richiamo a coppie.
Matematicamente,
$$FMS=\frac{TP}{\sqrt{\left(TP+FP\right)\left(TP+FN\right)}}$$Qui, TP = True Positive - numero di coppie di punti appartenenti agli stessi cluster sia nelle etichette vere che in quelle previste.
FP = False Positive - numero di coppie di punti appartenenti agli stessi cluster nelle etichette vere ma non nelle etichette previste.
FN = False Negative - numero di coppie di punti appartenenti agli stessi cluster nelle etichette previste ma non nelle etichette vere.
L'apprendimento di Scikit ha il modulo sklearn.metrics.fowlkes_mallows_score -
Esempio
from sklearn.metrics.cluster import fowlkes_mallows_score
labels_true = [0, 0, 1, 1, 1, 1]
labels_pred = [0, 0, 2, 2, 3, 3]
fowlkes_mallows__score (labels_true, labels_pred)Produzione
0.6546536707079771Coefficiente di sagoma
La funzione Silhouette calcolerà il coefficiente di sagoma medio di tutti i campioni utilizzando la distanza media intra-cluster e la distanza media del cluster più vicino per ciascun campione.
Matematicamente,
$$S=\left(b-a\right)/max\left(a,b\right)$$Qui, a è la distanza intra-cluster.
e, b è la distanza media dell'ammasso più vicino.
Lo Scikit impara ad avere sklearn.metrics.silhouette_score modulo -
Esempio
from sklearn import metrics.silhouette_score
from sklearn.metrics import pairwise_distances
from sklearn import datasets
import numpy as np
from sklearn.cluster import KMeans
dataset = datasets.load_iris()
X = dataset.data
y = dataset.target
kmeans_model = KMeans(n_clusters = 3, random_state = 1).fit(X)
labels = kmeans_model.labels_
silhouette_score(X, labels, metric = 'euclidean')Produzione
0.5528190123564091Matrice di contingenza
Questa matrice riporterà la cardinalità dell'intersezione per ogni coppia fidata di (vero, previsto). La matrice di confusione per i problemi di classificazione è una matrice di contingenza quadrata.
Lo Scikit impara ad avere sklearn.metrics.contingency_matrix modulo.
Esempio
from sklearn.metrics.cluster import contingency_matrix
x = ["a", "a", "a", "b", "b", "b"]
y = [1, 1, 2, 0, 1, 2]
contingency_matrix(x, y)Produzione
array([
[0, 2, 1],
[1, 1, 1]
])La prima riga dell'output sopra mostra che tra tre campioni il cui vero cluster è "a", nessuno di loro è in 0, due di sono in 1 e 1 è in 2. D'altra parte, la seconda riga mostra che tra tre campioni il cui vero cluster è "b", 1 è in 0, 1 è in 1 e 1 è in 2.
Riduzione della dimensionalità, un metodo di apprendimento automatico senza supervisione viene utilizzato per ridurre il numero di variabili di funzionalità per ciascun campione di dati selezionando un insieme di funzionalità principali. Principal Component Analysis (PCA) è uno degli algoritmi popolari per la riduzione della dimensionalità.
PCA esatto
Principal Component Analysis (PCA) viene utilizzato per la riduzione della dimensionalità lineare utilizzando Singular Value Decomposition(SVD) dei dati per proiettarli in uno spazio dimensionale inferiore. Durante la decomposizione mediante PCA, i dati di input vengono centrati ma non scalati per ciascuna funzione prima dell'applicazione dell'SVD.
La libreria Scikit-learn ML fornisce sklearn.decomposition.PCAmodulo implementato come un oggetto trasformatore che apprende n componenti nel suo metodo fit (). Può anche essere utilizzato su nuovi dati per proiettarli su questi componenti.
Esempio
L'esempio seguente utilizzerà il modulo sklearn.decomposition.PCA per trovare i 5 migliori componenti principali dal set di dati del diabete degli indiani Pima.
from pandas import read_csv
from sklearn.decomposition import PCA
path = r'C:\Users\Leekha\Desktop\pima-indians-diabetes.csv'
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', ‘class']
dataframe = read_csv(path, names = names)
array = dataframe.values
X = array[:,0:8]
Y = array[:,8]
pca = PCA(n_components = 5)
fit = pca.fit(X)
print(("Explained Variance: %s") % (fit.explained_variance_ratio_))
print(fit.components_)Produzione
Explained Variance: [0.88854663 0.06159078 0.02579012 0.01308614 0.00744094]
[
[-2.02176587e-03 9.78115765e-02 1.60930503e-02 6.07566861e-029.93110844e-01 1.40108085e-02 5.37167919e-04 -3.56474430e-03]
[-2.26488861e-02 -9.72210040e-01 -1.41909330e-01 5.78614699e-029.46266913e-02 -4.69729766e-02 -8.16804621e-04 -1.40168181e-01]
[-2.24649003e-02 1.43428710e-01 -9.22467192e-01 -3.07013055e-012.09773019e-02 -1.32444542e-01 -6.39983017e-04 -1.25454310e-01]
[-4.90459604e-02 1.19830016e-01 -2.62742788e-01 8.84369380e-01-6.55503615e-02 1.92801728e-01 2.69908637e-03 -3.01024330e-01]
[ 1.51612874e-01 -8.79407680e-02 -2.32165009e-01 2.59973487e-01-1.72312241e-04 2.14744823e-02 1.64080684e-03 9.20504903e-01]
]PCA incrementale
Incremental Principal Component Analysis (IPCA) viene utilizzato per affrontare la più grande limitazione dell'analisi dei componenti principali (PCA) e cioè PCA supporta solo l'elaborazione batch, significa che tutti i dati di input da elaborare devono essere contenuti nella memoria.
La libreria Scikit-learn ML fornisce sklearn.decomposition.IPCA modulo che rende possibile implementare Out-of-Core PCA sia utilizzando il suo partial_fit metodo su blocchi di dati prelevati in sequenza o abilitando l'uso di np.memmap, un file mappato in memoria, senza caricare l'intero file in memoria.
Come per la PCA, durante la decomposizione tramite IPCA, i dati di input vengono centrati ma non ridimensionati per ciascuna funzione prima dell'applicazione dell'SVD.
Esempio
L'esempio seguente userà sklearn.decomposition.IPCA modulo su Sklearn digit dataset.
from sklearn.datasets import load_digits
from sklearn.decomposition import IncrementalPCA
X, _ = load_digits(return_X_y = True)
transformer = IncrementalPCA(n_components = 10, batch_size = 100)
transformer.partial_fit(X[:100, :])
X_transformed = transformer.fit_transform(X)
X_transformed.shapeProduzione
(1797, 10)Qui, possiamo adattarci parzialmente a batch di dati più piccoli (come abbiamo fatto su 100 per batch) oppure puoi lasciare che il file fit() funzione per dividere i dati in batch.
PCA del kernel
Kernel Principal Component Analysis, un'estensione di PCA, ottiene una riduzione della dimensionalità non lineare utilizzando i kernel. Supporta entrambitransform and inverse_transform.
La libreria Scikit-learn ML fornisce sklearn.decomposition.KernelPCA modulo.
Esempio
L'esempio seguente userà sklearn.decomposition.KernelPCAmodulo su Sklearn digit dataset. Stiamo usando il kernel sigmoide.
from sklearn.datasets import load_digits
from sklearn.decomposition import KernelPCA
X, _ = load_digits(return_X_y = True)
transformer = KernelPCA(n_components = 10, kernel = 'sigmoid')
X_transformed = transformer.fit_transform(X)
X_transformed.shapeProduzione
(1797, 10)PCA utilizzando SVD randomizzato
L'analisi dei componenti principali (PCA) utilizzando SVD randomizzato viene utilizzata per proiettare i dati in uno spazio di dimensione inferiore preservando la maggior parte della varianza eliminando il vettore singolare dei componenti associati a valori singolari inferiori. Qui, ilsklearn.decomposition.PCA modulo con il parametro opzionale svd_solver=’randomized’ sarà molto utile.
Esempio
L'esempio seguente userà sklearn.decomposition.PCA modulo con il parametro opzionale svd_solver = 'randomized' per trovare i migliori 7 componenti principali dal dataset di Pima Indians Diabetes.
from pandas import read_csv
from sklearn.decomposition import PCA
path = r'C:\Users\Leekha\Desktop\pima-indians-diabetes.csv'
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
dataframe = read_csv(path, names = names)
array = dataframe.values
X = array[:,0:8]
Y = array[:,8]
pca = PCA(n_components = 7,svd_solver = 'randomized')
fit = pca.fit(X)
print(("Explained Variance: %s") % (fit.explained_variance_ratio_))
print(fit.components_)Produzione
Explained Variance: [8.88546635e-01 6.15907837e-02 2.57901189e-02 1.30861374e-027.44093864e-03 3.02614919e-03 5.12444875e-04]
[
[-2.02176587e-03 9.78115765e-02 1.60930503e-02 6.07566861e-029.93110844e-01 1.40108085e-02 5.37167919e-04 -3.56474430e-03]
[-2.26488861e-02 -9.72210040e-01 -1.41909330e-01 5.78614699e-029.46266913e-02 -4.69729766e-02 -8.16804621e-04 -1.40168181e-01]
[-2.24649003e-02 1.43428710e-01 -9.22467192e-01 -3.07013055e-012.09773019e-02 -1.32444542e-01 -6.39983017e-04 -1.25454310e-01]
[-4.90459604e-02 1.19830016e-01 -2.62742788e-01 8.84369380e-01-6.55503615e-02 1.92801728e-01 2.69908637e-03 -3.01024330e-01]
[ 1.51612874e-01 -8.79407680e-02 -2.32165009e-01 2.59973487e-01-1.72312241e-04 2.14744823e-02 1.64080684e-03 9.20504903e-01]
[-5.04730888e-03 5.07391813e-02 7.56365525e-02 2.21363068e-01-6.13326472e-03 -9.70776708e-01 -2.02903702e-03 -1.51133239e-02]
[ 9.86672995e-01 8.83426114e-04 -1.22975947e-03 -3.76444746e-041.42307394e-03 -2.73046214e-03 -6.34402965e-03 -1.62555343e-01]
]