鋭角、鈍角、直角三角形
次のように、鋭角、右角、鈍角を考えてみましょう。これらの角度の3番目の辺を閉じると、鋭角、右三角形、および鈍角の三角形が形成されます。これらの三角形には、常に少なくとも2つの鋭い三角形があります。3番目の角度は、三角形のタイプを決定します。3番目の角度が鋭角の場合、それは鋭角三角形です。3番目の角度が直角の場合、それは直角三角形です。3番目の角度が鈍角の場合、三角形は鈍角三角形です。
三角形は、最大で1つの直角と最大で1つの鈍角を持つことができます。
三角形は、常に3つの辺と3つの角度を持つポリゴンです。
三角形は、その角度に基づいて、鋭角、鈍角、直角三角形に分類できます。
アン acute triangle そのすべての角度が鋭いです。
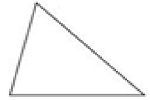
アン obtuse triangle 鈍角が1つあります。
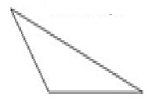
A right triangle 直角が1つあります。
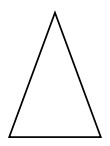
与えられた三角形を鋭角、鈍角、または直角三角形として識別します。
解決
Step 1:
与えられた三角形のすべての角度は鋭角です。
Step 2:
したがって、与えられた三角形は鋭角三角形です。
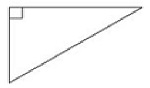
与えられた三角形を鋭角、鈍角、または直角三角形として識別します。
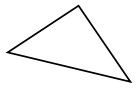
解決
Step 1:
与えられた三角形の角度の1つは直角です。
Step 2:
したがって、与えられた三角形は直角三角形です。