コンパイラ設計-クイックガイド
コンピューターは、ソフトウェアとハードウェアのバランスの取れた組み合わせです。ハードウェアは単なる機械装置であり、その機能は互換性のあるソフトウェアによって制御されています。ハードウェアは、ソフトウェアプログラミングのバイナリ言語に対応する電荷の形で命令を理解します。バイナリ言語には、0と1の2つのアルファベットしかありません。指示するには、ハードウェアコードをバイナリ形式で記述する必要があります。これは、単純に1と0のシリーズです。コンピュータープログラマーがそのようなコードを書くことは困難で面倒な作業になるでしょう。それが私たちがそのようなコードを書くためのコンパイラーを持っている理由です。
言語処理システム
私たちは、どのコンピュータシステムもハードウェアとソフトウェアでできていることを学びました。ハードウェアは、人間が理解できない言語を理解します。そのため、私たちは高水準言語でプログラムを作成します。これは、私たちが理解し、覚えやすいものです。次に、これらのプログラムは一連のツールとOSコンポーネントに送られ、マシンで使用できる目的のコードを取得します。これは言語処理システムとして知られています。
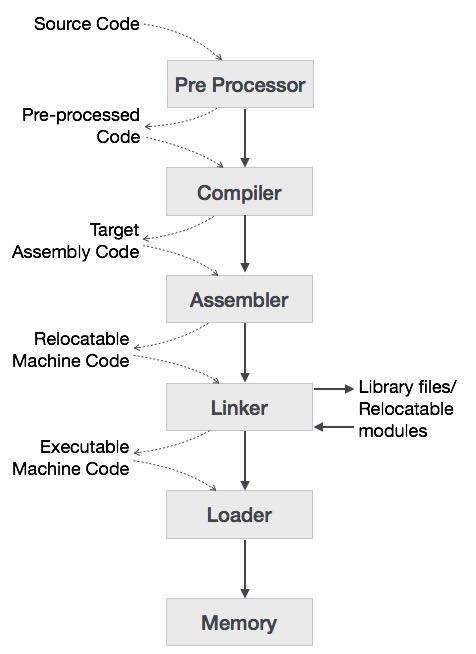
高水準言語は、さまざまな段階でバイナリ言語に変換されます。Acompilerは、高級言語をアセンブリ言語に変換するプログラムです。同様に、assembler は、アセンブリ言語をマシンレベルの言語に変換するプログラムです。
まず、Cコンパイラを使用したプログラムがホストマシンでどのように実行されるかを理解しましょう。
ユーザーはC言語(高級言語)でプログラムを作成します。
Cコンパイラは、プログラムをコンパイルして、アセンブリプログラム(低水準言語)に変換します。
次に、アセンブラはアセンブリプログラムをマシンコード(オブジェクト)に変換します。
リンカツールは、実行のためにプログラムのすべての部分をリンクするために使用されます(実行可能なマシンコード)。
ローダーがそれらすべてをメモリにロードしてから、プログラムが実行されます。
コンパイラの概念に直接飛び込む前に、コンパイラと緊密に連携する他のいくつかのツールを理解する必要があります。
プリプロセッサ
一般にコンパイラの一部と見なされるプリプロセッサは、コンパイラの入力を生成するツールです。マクロ処理、拡張、ファイルインクルード、言語拡張などを扱います。
通訳
コンパイラのようなインタプリタは、高級言語を低水準の機械語に翻訳します。違いは、ソースコードまたは入力の読み取り方法にあります。コンパイラは、ソースコード全体を一度に読み取り、トークンを作成し、セマンティクスをチェックし、中間コードを生成し、プログラム全体を実行し、多くのパスを伴う場合があります。対照的に、インタプリタは入力からステートメントを読み取り、それを中間コードに変換して実行し、次のステートメントを順番に取得します。エラーが発生した場合、インタプリタは実行を停止して報告します。一方、コンパイラは、いくつかのエラーが発生した場合でも、プログラム全体を読み取ります。
アセンブラ
アセンブラは、アセンブリ言語プログラムをマシンコードに変換します。アセンブラの出力はオブジェクトファイルと呼ばれ、マシン命令と、これらの命令をメモリに配置するために必要なデータの組み合わせが含まれています。
リンカ
リンカは、実行可能ファイルを作成するために、さまざまなオブジェクトファイルをリンクおよびマージするコンピュータプログラムです。これらのファイルはすべて、個別のアセンブラによってコンパイルされている可能性があります。リンカの主なタスクは、プログラム内で参照されるモジュール/ルーチンを検索して見つけ、これらのコードがロードされるメモリ位置を決定して、プログラム命令に絶対参照を持たせることです。
ローダ
ローダーはオペレーティングシステムの一部であり、実行可能ファイルをメモリにロードして実行する役割を果たします。プログラムのサイズ(命令とデータ)を計算し、そのためのメモリスペースを作成します。さまざまなレジスタを初期化して実行を開始します。
クロスコンパイラ
プラットフォーム(A)で実行され、プラットフォーム(B)の実行可能コードを生成できるコンパイラーは、クロスコンパイラーと呼ばれます。
ソースツーソースコンパイラ
あるプログラミング言語のソースコードを取得し、それを別のプログラミング言語のソースコードに変換するコンパイラは、ソースツーソースコンパイラと呼ばれます。
コンパイラアーキテクチャ
コンパイラーは、コンパイル方法に基づいて大きく2つのフェーズに分けることができます。
分析フェーズ
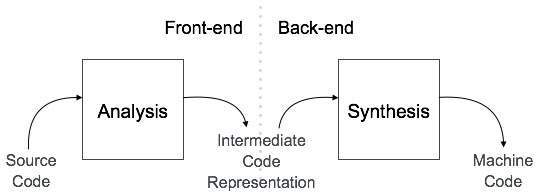
コンパイラのフロントエンドとして知られている、 analysis コンパイラのフェーズでは、ソースプログラムを読み取り、コア部分に分割してから、字句、文法、構文エラーをチェックします。分析フェーズでは、ソースプログラムとシンボルテーブルの中間表現が生成され、入力として合成フェーズに送られます。 。
合成段階
コンパイラのバックエンドとして知られている、 synthesis フェーズでは、中間ソースコード表現とシンボルテーブルを使用してターゲットプログラムを生成します。
コンパイラーには、多くのフェーズとパスがあります。
Pass :パスとは、プログラム全体をコンパイラーがトラバースすることを指します。
Phase:コンパイラのフェーズは識別可能なステージであり、前のステージからの入力を受け取り、次のステージの入力として使用できる出力を処理して生成します。パスには複数のフェーズを含めることができます。
コンパイラのフェーズ
コンパイルプロセスは、さまざまなフェーズのシーケンスです。各フェーズは、前のステージから入力を受け取り、ソースプログラムの独自の表現を持ち、その出力をコンパイラの次のフェーズにフィードします。コンパイラのフェーズを理解しましょう。
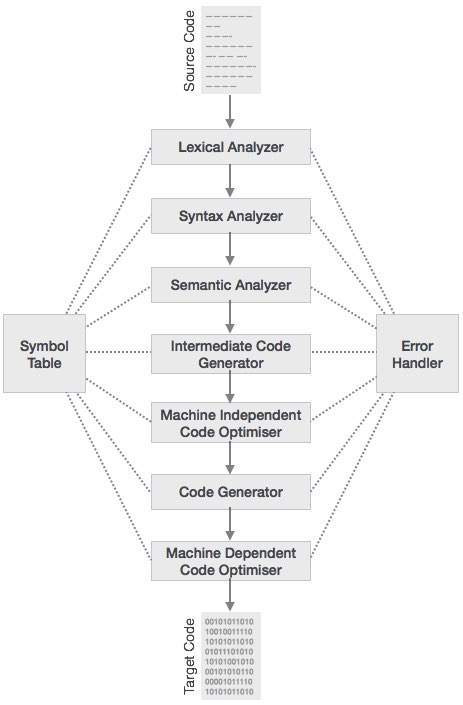
字句解析
スキャナーの最初のフェーズは、テキストスキャナーとして機能します。このフェーズでは、ソースコードを文字のストリームとしてスキャンし、意味のある語彙素に変換します。字句アナライザーは、これらの語彙素をトークンの形式で次のように表します。
<token-name, attribute-value>構文解析
次のフェーズは構文解析または parsing。字句解析によって生成されたトークンを入力として受け取り、解析ツリー(または構文ツリー)を生成します。このフェーズでは、トークンの配置がソースコードの文法に対してチェックされます。つまり、パーサーは、トークンによって作成された式が構文的に正しいかどうかをチェックします。
セマンティック分析
セマンティック分析は、構築された解析ツリーが言語の規則に従っているかどうかをチェックします。たとえば、値の割り当ては互換性のあるデータ型間で行われ、整数に文字列が追加されます。また、セマンティックアナライザーは、識別子、そのタイプ、および式を追跡します。識別子が使用前に宣言されているかどうかなど。セマンティックアナライザは、注釈付きの構文ツリーを出力として生成します。
中間コード生成
セマンティック分析の後、コンパイラはターゲットマシンのソースコードの中間コードを生成します。これは、いくつかの抽象マシンのプログラムを表します。それは高級言語と機械語の中間にあります。この中間コードは、ターゲットマシンコードへの変換が容易になるように生成する必要があります。
コードの最適化
次のフェーズでは、中間コードのコード最適化を行います。最適化は、不要なコード行を削除し、リソース(CPU、メモリ)を無駄にすることなくプログラムの実行を高速化するために、ステートメントのシーケンスを配置するものと見なすことができます。
コード生成
このフェーズでは、コードジェネレーターは中間コードの最適化された表現を取得し、それをターゲットの機械語にマップします。コードジェネレーターは、中間コードを(一般的に)再配置可能なマシンコードのシーケンスに変換します。マシンコードの一連の命令は、中間コードと同じようにタスクを実行します。
シンボルテーブル
これは、コンパイラーのすべてのフェーズを通じて維持されるデータ構造です。すべての識別子の名前とそのタイプがここに保存されます。シンボルテーブルを使用すると、コンパイラは識別子レコードをすばやく検索して取得することが容易になります。シンボルテーブルは、スコープ管理にも使用されます。
字句解析は、コンパイラーの最初のフェーズです。文の形で書かれた言語プリプロセッサから変更されたソースコードを取得します。字句解析プログラムは、ソースコード内の空白やコメントを削除することにより、これらの構文を一連のトークンに分割します。
字句解析プログラムが無効なトークンを検出すると、エラーが生成されます。字句アナライザーは構文アナライザーと緊密に連携します。ソースコードから文字ストリームを読み取り、正当なトークンをチェックし、必要に応じてデータを構文アナライザーに渡します。

トークン
語彙素は、トークン内の一連の文字(英数字)であると言われています。有効なトークンとして識別されるすべての語彙素には、いくつかの事前定義されたルールがあります。これらのルールは、パターンを使用した文法ルールによって定義されます。パターンはトークンになり得るものを説明し、これらのパターンは正規表現によって定義されます。
プログラミング言語では、キーワード、定数、識別子、文字列、数字、演算子、句読点記号をトークンと見なすことができます。
たとえば、C言語では、変数宣言行
int value = 100;トークンが含まれています:
int (keyword), value (identifier), = (operator), 100 (constant) and ; (symbol).トークンの仕様
言語理論がどのように次の用語を引き受けるかを理解しましょう。
アルファベット
シンボルの有限セット{0,1}は、バイナリアルファベットのセット{0,1,2,3,4,5,6,7,8,9、A、B、C、D、E、F}です。は16進アルファベットのセット、{az、AZ}は英語のアルファベットのセットです。
文字列
アルファベットの有限シーケンスは文字列と呼ばれます。文字列の長さは、アルファベットの合計出現回数です。たとえば、文字列の長さtutorialspointは14であり、| tutorialspoint |で示されます。= 14.アルファベットのない文字列、つまり長さがゼロの文字列は空の文字列と呼ばれ、ε(イプシロン)で表されます。
特別な記号
典型的な高級言語には、次の記号が含まれています。
| 算術記号 | 加算(+)、減算(-)、モジュロ(%)、乗算(*)、除算(/) |
| 句読点 | コンマ(、)、セミコロン(;)、ドット(。)、矢印(->) |
| 割り当て | = |
| 特別任務 | + =、/ =、* =、-= |
| 比較 | ==、!=、<、<=、>、> = |
| プリプロセッサ | # |
| 場所指定子 | & |
| 論理的 | &、&&、|、||、! |
| シフト演算子 | >>、>>>、<<、<<< |
言語
言語は、いくつかの有限のアルファベットのセットに対する有限の文字列のセットと見なされます。コンピューター言語は有限集合と見なされ、数学的に集合操作を実行できます。有限言語は正規表現で記述できます。
正規表現
字句解析プログラムは、手元の言語に属する有効な文字列/トークン/語彙素の有限セットのみをスキャンして識別する必要があります。言語ルールで定義されたパターンを検索します。
正規表現には、記号の有限文字列のパターンを定義することにより、有限言語を表現する機能があります。正規表現によって定義される文法は、regular grammar。正規文法で定義されている言語は、regular language。
正規表現は、パターンを指定するための重要な表記法です。各パターンは文字列のセットと一致するため、正規表現は文字列のセットの名前として機能します。プログラミング言語トークンは、正規言語で記述できます。正規表現の指定は、再帰的定義の一例です。正規言語は理解しやすく、効率的に実装できます。
正規表現が従う代数式は多数あり、正規表現を同等の形式に操作するために使用できます。
操作
言語に対するさまざまな操作は次のとおりです。
LとMの2つの言語の結合は次のように書かれています
LUM = {s | sはLであるか、sはMである}
2つの言語LとMの連結は次のように記述されます
LM = {st | sはLで、tはMです}
言語Lのクリーネ閉包は次のように書かれています
L * =言語Lの出現がゼロ以上。
表記法
rとsが言語L(r)とL(s)を表す正規表現である場合、
Union :(r)|(s)は、L(r)UL(s)を表す正規表現です。
Concatenation :(r)(s)は、L(r)L(s)を表す正規表現です。
Kleene closure :(r)*は(L(r))*を表す正規表現です。
(r)は、L(r)を表す正規表現です。
優先順位と結合性
- *、連結(。)、および| (パイプ記号)は結合性のままです
- *優先順位が最も高い
- 連結(。)の優先順位は2番目に高くなります。
- | (パイプ記号)は、すべての中で最も低い優先順位を持っています。
正規表現で言語の有効なトークンを表す
xが正規表現の場合、次のようになります。
x *は、xの出現が0回以上であることを意味します。
つまり、{e、x、xx、xxx、xxxx、…}を生成できます。
x +は、xが1回以上出現することを意味します。
つまり、{x、xx、xxx、xxxx…}またはxx *を生成できます。
バツ?xの最大1回の出現を意味します
つまり、{x}または{e}のいずれかを生成できます。
[az]はすべて英語の小文字のアルファベットです。
[AZ]はすべて英語の大文字のアルファベットです。
[0-9]は、数学で使用されるすべての自然な数字です。
正規表現を使用して記号の出現を表す
文字= [a –z]または[A– Z]
数字= 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9または[0-9]
記号= [+ | -]
正規表現を使用した言語トークンの表現
小数点=(符号)?(桁)+
識別子=(文字)(文字|数字)*
字句解析プログラムに残された唯一の問題は、言語のキーワードのパターンを指定する際に使用される正規表現の有効性をどのように検証するかです。広く受け入れられている解決策は、検証に有限オートマトンを使用することです。
有限オートマトン
有限オートマトンは、一連の記号を入力として受け取り、それに応じて状態を変更するステートマシンです。有限オートマトンは、正規表現の認識機能です。正規表現文字列が有限オートマトンに入力されると、リテラルごとにその状態が変更されます。入力文字列が正常に処理され、オートマトンが最終状態に達すると、受け入れられます。つまり、入力されたばかりの文字列は、手元の言語の有効なトークンであると言われます。
有限オートマトンの数学モデルは、次のもので構成されます。
- 有限の状態セット(Q)
- 入力記号の有限集合(Σ)
- 1つの開始状態(q0)
- 最終状態のセット(qf)
- 遷移関数(δ)
遷移関数(δ)は、状態の有限集合(Q)を入力記号の有限集合(Σ)にマップします。Q×Σ➔Q
有限オートマトン構築
L(r)を、ある有限オートマトン(FA)によって認識される正規言語とします。
States:FAの状態は円で表されます。州名は円の中に書かれています。
Start state:オートマトンが開始する状態は、開始状態と呼ばれます。開始状態には、その方向を指す矢印があります。
Intermediate states:すべての中間状態には、少なくとも2つの矢印があります。1つはそれらを指し、もう1つはそれらから指摘します。
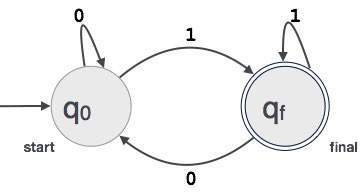
Final state:入力文字列が正常に解析された場合、オートマトンはこの状態であると予想されます。最終状態は二重円で表されます。奇数の矢印がそれを指し、偶数の矢印がそれを指している可能性があります。奇数の矢印の数は偶数より1つ多い、つまりodd = even+1。
Transition:ある状態から別の状態への遷移は、入力で目的のシンボルが見つかったときに発生します。移行時に、オートマトンは次の状態に移行するか、同じ状態を維持することができます。ある状態から別の状態への移動は、方向矢印として示され、矢印は目的の状態を指します。オートマトンが同じ状態のままである場合、状態からそれ自体を指す矢印が描画されます。
Example:FAは1桁で終わる任意の3桁の2進値を受け入れると仮定します。FA= {Q(q 0、q f)、Σ(0,1)、q 0、q f、δ}
最長一致ルール
字句解析プログラムがソースコードを読み取ると、コードを1文字ずつスキャンします。空白、演算子記号、または特殊記号が検出されると、単語が完成したと判断します。
For example:
int intvalue;'int'まで両方の語彙素をスキャンしている間、字句解析プログラムは、それがキーワードintであるか、識別子int値のイニシャルであるかを判別できません。
最長一致ルールでは、スキャンされる語彙素は、使用可能なすべてのトークンの中で最長の一致に基づいて決定する必要があると規定されています。
字句解析プログラムも次のようになります rule priorityここで、言語の予約語、たとえばキーワードは、ユーザー入力よりも優先されます。つまり、字句解析プログラムが既存の予約語と一致する語彙素を見つけた場合、エラーが生成されます。
構文解析または構文解析は、コンパイラーの第2フェーズです。この章では、パーサーの構築に使用される基本的な概念を学習します。
字句解析プログラムは、正規表現とパターンルールを使用してトークンを識別できることを確認しました。ただし、字句解析プログラムは、正規表現の制限により、特定の文の構文をチェックできません。正規表現では、括弧などのバランシングトークンをチェックできません。したがって、このフェーズでは、プッシュダウンオートマトンによって認識される文脈自由文法(CFG)を使用します。
一方、CFGは、以下に示すように、正規文法のスーパーセットです。

これは、すべての正規文法も文脈自由であることを意味しますが、正規文法の範囲を超えるいくつかの問題が存在します。CFGは、プログラミング言語の構文を記述するのに役立つツールです。
文脈自由文法
このセクションでは、最初に文脈自由文法の定義を確認し、構文解析テクノロジで使用される用語を紹介します。
文脈自由文法には4つの要素があります。
一連の non-terminals(V)。非終端記号は、文字列のセットを表す構文変数です。非終端記号は、文法によって生成される言語の定義に役立つ文字列のセットを定義します。
トークンのセット。 terminal symbols(Σ)。端子は、ストリングが形成される基本的な記号です。
一連の productions(P)。文法の生成では、終端記号と非終端記号を組み合わせて文字列を形成する方法を指定します。各作品は、non-terminal プロダクションの左側、矢印、一連のトークンおよび/または on- terminals、プロダクションの右側と呼ばれます。
非終端記号の1つは、開始記号(S)として指定されます。生産が始まるところから。
文字列は、非終端記号(最初は開始記号)をプロダクションの右側で繰り返し置き換えることにより、開始記号から派生します。
例
正規表現では記述できない回文言語の問題を取り上げます。つまり、L = {w | W = W R }正規言語ではありません。ただし、以下に示すように、CFGを使用して説明できます。
G = ( V, Σ, P, S )どこ:
V = { Q, Z, N }
Σ = { 0, 1 }
P = { Q → Z | Q → N | Q → ℇ | Z → 0Q0 | N → 1Q1 }
S = { Q }この文法は、1001、11100111、00100、1010101、11111などの回文言語を記述します。
構文アナライザー
構文アナライザーまたはパーサーは、トークンストリームの形式で字句アナライザーからの入力を受け取ります。パーサーは、ソースコード(トークンストリーム)を本番ルールと照合して分析し、コード内のエラーを検出します。このフェーズの出力はparse tree。

このようにして、パーサーは2つのタスクを実行します。つまり、コードの解析、エラーの検索、およびフェーズの出力としての解析ツリーの生成です。
プログラムにエラーが存在する場合でも、パーサーはコード全体を解析することが期待されています。パーサーはエラー回復戦略を使用します。これについては、この章の後半で学習します。
導出
派生は基本的に、入力文字列を取得するための一連の生成ルールです。構文解析中に、いくつかのセンテンス形式の入力に対して2つの決定を行います。
- 交換する非終端記号を決定します。
- 非終端記号が置き換えられるプロダクションルールを決定します。
どの非終端記号をプロダクションルールに置き換えるかを決定するには、2つのオプションがあります。
左端の派生
入力のセンテンス形式がスキャンされ、左から右に置き換えられる場合、それは左端の派生と呼ばれます。左端の派生によって導出されたセンテンス形式は、左センテンス形式と呼ばれます。
右端の派生
入力をスキャンして、右から左にプロダクションルールに置き換えると、右端からの派生と呼ばれます。右端の派生から派生したセンテンス形式は、右センテンス形式と呼ばれます。
Example
制作ルール:
E → E + E
E → E * E
E → id入力文字列:id + id * id
左端の派生は次のとおりです。
E → E * E
E → E + E * E
E → id + E * E
E → id + id * E
E → id + id * id左端の非終端記号が常に最初に処理されることに注意してください。
右端の派生は次のとおりです。
E → E + E
E → E + E * E
E → E + E * id
E → E + id * id
E → id + id * id解析ツリー
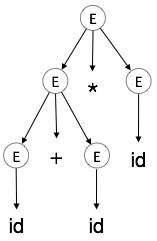
解析ツリーは、派生をグラフィカルに表現したものです。文字列が開始記号からどのように派生するかを確認すると便利です。派生の開始記号は、解析ツリーのルートになります。最後のトピックの例でこれを見てみましょう。
a + b * cの左端の導出を取ります
左端の派生は次のとおりです。
E → E * E
E → E + E * E
E → id + E * E
E → id + id * E
E → id + id * idステップ1:
| E→E * E |
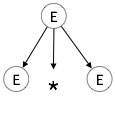
|
ステップ2:
| E→E + E * E |
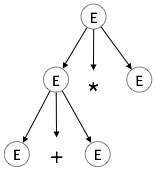
|
ステップ3:
| E→id + E * E |
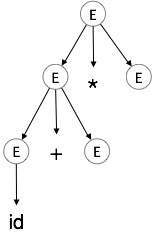
|
ステップ4:
| E→id + id * E |
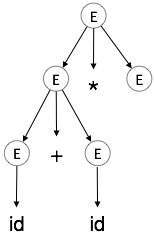
|
ステップ5:
| E→id + id * id |
|
解析ツリーの場合:
- すべてのリーフノードはターミナルです。
- すべての内部ノードは非終端記号です。
- インオーダートラバーサルは、元の入力文字列を提供します。
解析ツリーは、演算子の結合性と優先順位を示します。最も深いサブツリーが最初にトラバースされるため、そのサブツリー内の演算子は、親ノード内にある演算子よりも優先されます。
構文解析の種類
構文アナライザーは、文脈自由文法によって定義された生成規則に従います。プロダクションルールの実装方法(派生)は、解析をトップダウン解析とボトムアップ解析の2つのタイプに分けます。
トップダウン構文解析
パーサーが開始シンボルから解析ツリーの構築を開始し、開始シンボルを入力に変換しようとする場合、これはトップダウン構文解析と呼ばれます。
Recursive descent parsing:これは、トップダウン構文解析の一般的な形式です。入力を処理するために再帰的プロシージャを使用するため、再帰的と呼ばれます。再帰下降構文解析はバックトラックに悩まされます。
Backtracking:つまり、プロダクションの1つの派生が失敗した場合、構文アナライザーは同じプロダクションの異なるルールを使用してプロセスを再開します。この手法では、入力文字列を複数回処理して、適切なプロダクションを決定する場合があります。
ボトムアップ構文解析
名前が示すように、ボトムアップ解析は入力シンボルから始まり、開始シンボルまで解析ツリーを構築しようとします。
Example:
入力文字列:a + b * c
制作ルール:
S → E
E → E + T
E → E * T
E → T
T → idボトムアップ構文解析を始めましょう
a + b * c入力を読み取り、プロダクションが入力と一致するかどうかを確認します。
a + b * c
T + b * c
E + b * c
E + T * c
E * c
E * T
E
Sあいまいさ
文法Gは、少なくとも1つの文字列に対して複数の解析ツリー(左または右の派生)がある場合、あいまいであると言われます。
Example
E → E + E
E → E – E
E → id文字列id + id – idの場合、上記の文法は2つの解析ツリーを生成します。

あいまいな文法によって生成される言語は、 inherently ambiguous。文法のあいまいさは、コンパイラーの構築には適していません。あいまいさを自動的に検出して削除する方法はありませんが、あいまいさのない文法全体を書き直すか、結合性と優先順位の制約を設定して従うことで削除できます。
結合性
オペランドの両側に演算子がある場合、演算子がこのオペランドをとる側は、それらの演算子の結合性によって決定されます。演算が左結合の場合、オペランドは左演算子によって取得されます。演算が右結合の場合、右演算子がオペランドを取得します。
Example
加算、乗算、減算、除算などの演算は結合性のままです。式に次のものが含まれている場合:
id op id op id次のように評価されます。
(id op id) op idたとえば、(id + id)+ id
べき乗のような演算は正しく結合します。つまり、同じ式での評価の順序は次のようになります。
id op (id op id)たとえば、id ^(id ^ id)
優先順位
2つの異なる演算子が共通のオペランドを共有する場合、演算子の優先順位によって、どちらがオペランドを使用するかが決まります。つまり、2 + 3 * 4は、2つの異なる解析ツリーを持つことができます。1つは(2 + 3)* 4に対応し、もう1つは2 +(3 * 4)に対応します。演算子間の優先順位を設定することにより、この問題を簡単に取り除くことができます。前の例のように、数学的に*(乗算)は+(加算)よりも優先されるため、式2 + 3 * 4は常に次のように解釈されます。
2 + (3 * 4)これらの方法は、言語またはその文法のあいまいさの可能性を減らします。
左再帰
文法の派生に「A」自体が左端の記号として含まれている非終端記号「A」がある場合、文法は左再帰になります。左再帰文法は、トップダウンパーサーにとって問題のある状況であると考えられています。トップダウンパーサーは、それ自体が非終端記号である開始記号から解析を開始します。そのため、パーサーがその派生で同じ非終端記号に遭遇すると、左側の非終端記号の構文解析をいつ停止するかを判断するのが難しくなり、無限ループに入ります。
Example:
(1) A => Aα | β
(2) S => Aα | β
A => Sd(1)は、即時左再帰の例です。ここで、Aは任意の非終端記号であり、αは非終端記号の文字列を表します。
(2)は間接左再帰の例です。
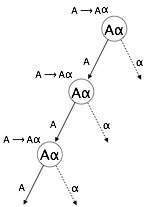
トップダウンパーサーは最初にAを解析します。これにより、A自体で構成される文字列が生成され、パーサーは永久にループに入る可能性があります。
左再帰の除去
左再帰を削除する1つの方法は、次の手法を使用することです。
生産
A => Aα | β以下の作品に変換されます
A => βA’
A => αA’ | εこれは文法から派生した文字列には影響しませんが、すぐに左再帰を削除します。
2番目の方法は、次のアルゴリズムを使用することです。これにより、すべての直接および間接の左再帰が排除されます。
Algorithm
START
Arrange non-terminals in some order like A1, A2, A3,…, An
for each i from 1 to n
{
for each j from 1 to i-1
{
replace each production of form Ai⟹Aj
with Ai ⟹ δ1 | δ2 | δ3 |…|
where Aj ⟹ δ1 | δ2|…| δn are current Aj productions
}
}
eliminate immediate left-recursion
ENDExample
プロダクションセット
S => Aα | β
A => Sd上記のアルゴリズムを適用した後、
S => Aα | β
A => Aαd | βd次に、最初の手法を使用して、すぐに左再帰を削除します。
A => βdA’
A => αdA’ | ε現在、どのプロダクションにも直接または間接の左再帰はありません。
左ファクタリング
複数の文法生成ルールに共通のプレフィックス文字列がある場合、トップダウンパーサーは、手元の文字列を解析するためにどの生成を行う必要があるかを選択できません。
Example
トップダウンパーサーが次のようなプロダクションに遭遇した場合
A ⟹ αβ | α | …次に、両方のプロダクションが同じ端末(または非端末)から開始しているため、文字列を解析するためにどのプロダクションに従うかを決定できません。この混乱を取り除くために、左因数分解と呼ばれる手法を使用します。
左因数分解は文法を変換して、トップダウンパーサーに役立つようにします。この手法では、共通のプレフィックスごとに1つのプロダクションを作成し、残りの派生は新しいプロダクションによって追加されます。
Example
上記の作品は次のように書くことができます
A => αA’
A’=> β | | …現在、パーサーにはプレフィックスごとに1つのプロダクションしかないため、決定が容易になります。
最初と次のセット
パーサーテーブル構築の重要な部分は、最初にセットを作成し、次にセットを作成することです。これらのセットは、派生における任意の端末の実際の位置を提供できます。これは、T [A、t] =αを何らかの生成ルールに置き換える決定が行われる解析テーブルを作成するために行われます。
最初のセット
このセットは、非終端記号によって最初の位置でどの終端記号が派生するかを知るために作成されます。例えば、
α → t βつまり、αは最初の位置でt(端子)を導き出します。したがって、t∈FIRST(α)。
最初のセットを計算するためのアルゴリズム
FIRST(α)セットの定義を見てください。
- αが端子の場合、FIRST(α)= {α}。
- αが非終端記号であり、α→ℇが生成である場合、FIRST(α)= {ℇ}。
- αが非終端記号であり、α→1 2 3…nであり、FIRST()にtが含まれている場合、tはFIRST(α)にあります。
最初のセットは次のように見ることができます:FIRST(α)= {t | α→ * tβ}∪{ℇ| α→ * ε}
セットに従ってください
同様に、プロダクションルールで非終端記号αの直後に続く終端記号を計算します。非終端記号が何を生成できるかは考慮しませんが、代わりに、非終端記号の生成に続く次の終端記号が何であるかを確認します。
フォローセットを計算するためのアルゴリズム:
αが開始記号の場合、FOLLOW()= $
αが非終端記号であり、生成がα→ABである場合、FIRST(B)はℇを除いてFOLLOW(A)にあります。
αが非終端記号であり、生成α→AB(Bℇ)の場合、FOLLOW(A)はFOLLOW(α)にあります。
フォローセットは次のように見ることができます:FOLLOW(α)= {t | S *αt*}
エラー回復戦略
パーサーは、プログラムのエラーを検出して報告できる必要があります。エラーが発生した場合、パーサーはそれを処理し、残りの入力の解析を続行できる必要があります。ほとんどの場合、パーサーからエラーをチェックすることが期待されますが、コンパイルプロセスのさまざまな段階でエラーが発生する可能性があります。プログラムには、さまざまな段階で次の種類のエラーが発生する可能性があります。
Lexical :誤って入力された識別子の名前
Syntactical :セミコロンの欠落または不均衡な括弧
Semantical :互換性のない値の割り当て
Logical :コードに到達できない、無限ループ
コード内のエラーを処理するためにパーサーに実装できる4つの一般的なエラー回復戦略があります。
パニックモード
パーサーがステートメントのどこかでエラーを検出すると、誤った入力からセミコロンなどの区切り文字への入力を処理しないため、ステートメントの残りの部分が無視されます。これはエラー回復の最も簡単な方法であり、パーサーが無限ループを発生するのを防ぎます。
ステートメントモード
パーサーでエラーが発生すると、ステートメントの残りの入力でパーサーが先に解析できるように、修正措置を講じようとします。たとえば、欠落しているセミコロンを挿入したり、コンマをセミコロンに置き換えたりします。1つの間違った修正により無限ループが発生する可能性があるため、パーサーの設計者はここで注意する必要があります。
エラープロダクション
コードで発生する可能性のあるいくつかの一般的なエラーは、コンパイラの設計者に知られています。さらに、設計者は、これらのエラーが発生したときに誤った構成を生成するプロダクションとして使用される拡張文法を作成できます。
グローバル修正
パーサーは、手元にあるプログラム全体を考慮し、プログラムの目的を理解しようとし、エラーのない最も近いプログラムを見つけようとします。誤った入力(ステートメント)Xが供給されると、最も近いエラーのないステートメントYの解析ツリーが作成されます。これにより、パーサーはソースコードに最小限の変更を加えることができますが、の複雑さ(時間とスペース)が原因です。この戦略は、まだ実際には実装されていません。
抽象構文木
解析ツリー表現は、実際に必要なものよりも多くの詳細が含まれているため、コンパイラで簡単に解析することはできません。例として、次の解析ツリーを取り上げます。

注意深く見ると、リーフノードのほとんどが親ノードの単一の子であることがわかります。この情報は、次のフェーズに送る前に削除できます。追加情報を非表示にすることで、次のようなツリーを取得できます。
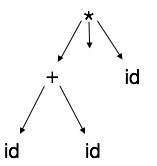
抽象ツリーは次のように表すことができます。
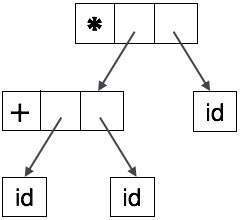
ASTは、不要な情報が最も少ないコンパイラの重要なデータ構造です。ASTは解析ツリーよりもコンパクトであり、コンパイラーで簡単に使用できます。
構文アナライザーの制限
構文アナライザーは、字句アナライザーからトークンの形式で入力を受け取ります。字句アナライザーは、構文アナライザーによって提供されるトークンの有効性に責任があります。構文アナライザーには、次の欠点があります。
- トークンが有効かどうかを判断できません。
- トークンが使用される前に宣言されているかどうかを判断することはできません。
- トークンが使用される前に初期化されているかどうかを判断できません。
- トークンタイプに対して実行された操作が有効かどうかを判断することはできません。
これらのタスクは、セマンティック分析で学習するセマンティックアナライザーによって実行されます。
構文解析フェーズで、パーサーが解析ツリーを構築する方法を学びました。そのフェーズで構築されたプレーンな解析ツリーは、ツリーの評価方法に関する情報を持たないため、通常、コンパイラーには役に立ちません。言語の規則を作る文脈自由文法の生成は、それらをどのように解釈するかに対応していません。
例えば
E → E + T上記のCFGプロダクションには、それに関連付けられたセマンティックルールがなく、プロダクションの意味を理解するのに役立ちません。
セマンティクス
言語のセマンティクスは、トークンや構文構造など、その構造に意味を提供します。セマンティクスは、記号、それらのタイプ、およびそれらの相互関係を解釈するのに役立ちます。セマンティック分析は、ソースプログラムで構築された構文構造が何らかの意味を引き出すかどうかを判断します。
CFG + semantic rules = Syntax Directed Definitions例えば:
int a = “value”;字句解析および構文解析フェーズでは、字句および構造的に正しいため、エラーを発行するべきではありませんが、割り当てのタイプが異なるため、意味エラーを生成する必要があります。これらのルールは、言語の文法によって設定され、セマンティック分析で評価されます。セマンティック分析では、次のタスクを実行する必要があります。
- スコープ解決
- 型チェック
- 配列境界チェック
セマンティックエラー
セマンティックアナライザが認識すると予想されるセマンティクスエラーのいくつかについて説明しました。
- 型の不一致
- 宣言されていない変数
- 予約済みの識別子の誤用。
- スコープ内の変数の複数の宣言。
- スコープ外の変数へのアクセス。
- 実際のパラメータと正式なパラメータの不一致。
属性文法
属性文法は、状況依存情報を提供するために、いくつかの追加情報(属性)が1つ以上の非終端記号に追加される特殊な形式の文脈自由文法です。各属性には、整数、浮動小数点数、文字、文字列、式など、明確に定義された値のドメインがあります。
属性文法は、文脈自由文法にセマンティクスを提供するための媒体であり、プログラミング言語の構文とセマンティクスを指定するのに役立ちます。属性文法(解析ツリーとして表示される場合)は、ツリーのノード間で値または情報を渡すことができます。
Example:
E → E + T { E.value = E.value + T.value }CFGの右側には、文法の解釈方法を指定するセマンティックルールが含まれています。ここでは、非終端記号EとTの値が加算され、結果が非終端記号Eにコピーされます。
セマンティック属性は、解析時にドメインから値に割り当てられ、割り当てまたは条件のときに評価される場合があります。属性が値を取得する方法に基づいて、属性は大きく2つのカテゴリに分類できます。合成属性と継承属性です。
合成された属性
これらの属性は、子ノードの属性値から値を取得します。説明のために、次のプロダクションを想定します。
S → ABCSがその子ノード(A、B、C)から値を取得している場合、ABCの値はSに合成されるため、合成された属性であると言われます。
前の例(E→E + T)のように、親ノードEはその子ノードから値を取得します。合成された属性は、親ノードまたは兄弟ノードから値を取得することはありません。
継承された属性
合成された属性とは対照的に、継承された属性は親や兄弟から値を取得できます。次のプロダクションのように、
S → ABCAはS、B、およびCから値を取得できます。BはS、A、およびCから値を取得できます。同様に、CはS、A、およびBから値を取得できます。
Expansion :文法規則に従って非終端記号が終端記号に展開される場合
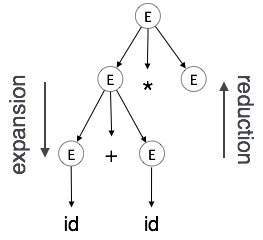
Reduction:文法規則に従って、終端記号が対応する非終端記号に縮小された場合。構文木はトップダウンで左から右に解析されます。削減が発生するたびに、対応するセマンティックルール(アクション)を適用します。
セマンティック分析では、Syntax DirectedTranslationsを使用して上記のタスクを実行します。
セマンティックアナライザーは、前の段階(構文解析)からAST(抽象構文木)を受け取ります。
セマンティックアナライザーは、属性ASTと呼ばれる属性情報をASTに添付します。
属性は2つのタプル値、<属性名、属性値>です。
例えば:
int value = 5;
<type, “integer”>
<presentvalue, “5”>すべてのプロダクションに対して、セマンティックルールを添付します。
S属性のSDT
SDTが合成された属性のみを使用する場合、それはS属性SDTと呼ばれます。これらの属性は、生成後にセマンティックアクションが記述されたS属性のSDTを使用して評価されます(右側)。
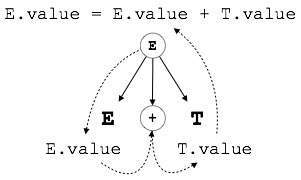
上に示したように、親ノードの値は子ノードの値に依存するため、S属性のSDTの属性はボトムアップ構文解析で評価されます。
L属性のSDT
この形式のSDTは、合成属性と継承属性の両方を使用しますが、正しい兄弟から値を取得しないという制限があります。
L属性のSDTでは、非終端記号はその親、子、および兄弟ノードから値を取得できます。次のプロダクションのように
S → ABCSは、A、B、およびC(合成)から値を取得できます。AはSからのみ値を取ることができます。BはSとAから値を取得できます。CはS、A、およびBから値を取得できます。非終端記号はその右側の兄弟から値を取得できません。
L属性SDTの属性は、深さ優先および左から右への解析方法によって評価されます。
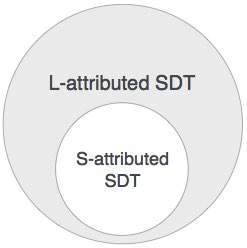
定義がS属性である場合、L属性定義はS属性定義を含むため、L属性でもあると結論付けることができます。
前の章では、構文解析に関連する基本的な概念を理解しました。この章では、利用可能なさまざまなタイプのパーサー構築方法について学習します。
解析は、解析ツリーの構築方法に基づいて、トップダウンまたはボトムアップとして定義できます。

トップダウン構文解析
前の章で、トップダウン解析手法が入力を解析し、ルートノードから徐々にリーフノードに移動する解析ツリーの構築を開始することを学びました。トップダウン構文解析のタイプを以下に示します。
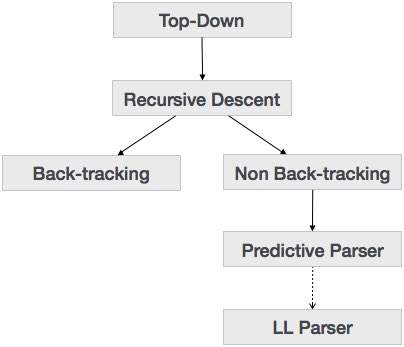
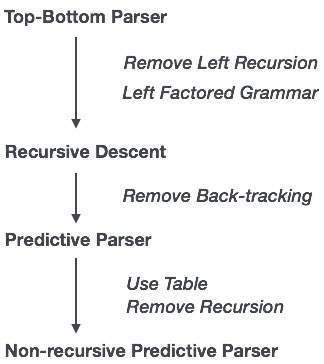
再帰下降構文解析
再帰下降は、解析ツリーを上から構築し、入力を左から右に読み取るトップダウン解析手法です。これは、すべての終端記号と非終端記号エンティティのプロシージャを使用します。この解析手法は、入力を再帰的に解析して解析ツリーを作成します。解析ツリーには、バックトラッキングが必要な場合と不要な場合があります。しかし、それに関連する文法(因数分解されていない場合)は、バックトラックを回避することはできません。バックトラッキングを必要としない再帰下降構文解析の形式は、次のように知られています。predictive parsing。
この構文解析手法は、本質的に再帰的である文脈自由文法を使用するため、再帰的と見なされます。
バックトラッキング
トップダウンパーサーはルートノード(開始記号)から開始し、入力文字列を本番ルールと照合して置き換えます(一致する場合)。これを理解するために、次のCFGの例を見てください。
S → rXd | rZd
X → oa | ea
Z → ai入力文字列の場合:トップダウンパーサーであるreadは、次のように動作します。
プロダクションルールのSで始まり、その歩留まりを入力の左端の文字、つまり「r」に一致させます。S(S→rXd)の生成そのものがそれに一致します。したがって、トップダウンパーサーは次の入力文字(つまり「e」)に進みます。パーサーは非端末「X」を展開しようとし、左からその生成をチェックします(X→oa)。次の入力記号と一致しません。したがって、トップダウンパーサーは、Xの次の生成ルール(X→ea)を取得するためにバックトラックします。
これで、パーサーはすべての入力文字を順序付けられた方法で照合します。文字列が受け入れられます。
|
|
|
|
|
予測パーサー
予測パーサーは再帰下降パーサーであり、入力文字列を置き換えるために使用されるプロダクションを予測する機能があります。予測パーサーはバックトラックの影響を受けません。
そのタスクを実行するために、予測パーサーは、次の入力シンボルを指す先読みポインターを使用します。パーサーのバックトラッキングを無料にするために、予測パーサーは文法にいくつかの制約を課し、LL(k)文法として知られる文法のクラスのみを受け入れます。
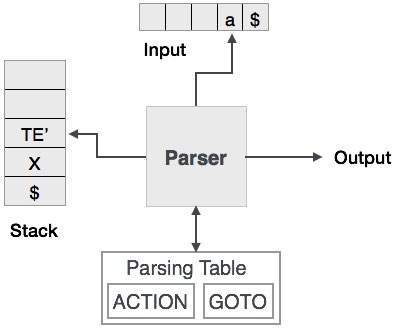
予測解析では、スタックと解析テーブルを使用して入力を解析し、解析ツリーを生成します。スタックと入力の両方に終了記号が含まれています$スタックが空で、入力が消費されていることを示します。パーサーは解析テーブルを参照して、入力要素とスタック要素の組み合わせを決定します。
再帰下降構文解析では、パーサーは入力の単一インスタンスに対して複数のプロダクションから選択できますが、予測パーサーでは、各ステップで選択できるプロダクションは最大で1つです。入力文字列に一致するプロダクションがないために、解析手順が失敗する場合があります。
LLパーサー
LLパーサーはLL文法を受け入れます。LL文法は文脈自由文法のサブセットですが、簡単な実装を実現するために、簡略化されたバージョンを取得するためのいくつかの制限があります。LL文法は、再帰下降またはテーブル駆動の両方のアルゴリズムを使用して実装できます。
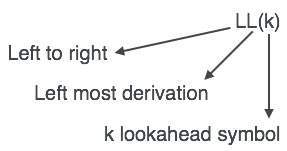
LLパーサーはLL(k)として表されます。LL(k)の最初のLは入力を左から右に解析し、LL(k)の2番目のLは左端の派生を表し、k自体は先読みの数を表します。通常、k = 1であるため、LL(k)はLL(1)と書くこともできます。
LL解析アルゴリズム
テーブルのサイズはkの値とともに指数関数的に増加するため、パーサーの説明については決定論的なLL(1)に固執する場合があります。次に、特定の文法がLL(1)でない場合、通常、特定のkについてはLL(k)ではありません。
以下に、LL(1)解析のアルゴリズムを示します。
Input:
string ω
parsing table M for grammar G
Output:
If ω is in L(G) then left-most derivation of ω,
error otherwise.
Initial State : $S on stack (with S being start symbol) ω$ in the input buffer
SET ip to point the first symbol of ω$.
repeat
let X be the top stack symbol and a the symbol pointed by ip.
if X∈ Vt or $
if X = a
POP X and advance ip.
else
error()
endif
else /* X is non-terminal */
if M[X,a] = X → Y1, Y2,... Yk
POP X
PUSH Yk, Yk-1,... Y1 /* Y1 on top */
Output the production X → Y1, Y2,... Yk
else
error()
endif
endif
until X = $ /* empty stack */A-> alpha |の場合、文法GはLL(1)です。bはGの2つの異なる作品です:
ターミナルがない場合、アルファとベータの両方がaで始まる文字列を派生させます。
アルファとベータの最大で1つが空の文字列を導出できます。
beta => tの場合、alphaはFOLLOW(A)の端末で始まる文字列を導出しません。
ボトムアップ構文解析
ボトムアップ解析は、ツリーのリーフノードから始まり、ルートノードに到達するまで上方向に機能します。ここでは、文から始めて、開始記号に到達するために逆の方法で生成ルールを適用します。以下の画像は、利用可能なボトムアップパーサーを示しています。

Shift-Reduce構文解析
Shift-reduce構文解析は、ボトムアップ構文解析に2つの固有のステップを使用します。これらのステップは、シフトステップおよびリデュースステップとして知られています。
Shift step:シフトステップとは、シフトシンボルと呼ばれる次の入力シンボルへの入力ポインタの前進を指します。このシンボルはスタックにプッシュされます。シフトされたシンボルは、解析ツリーの単一ノードとして扱われます。
Reduce step:パーサーが完全な文法規則(RHS)を見つけて、それを(LHS)に置き換える場合、それはreduce-stepとして知られています。これは、スタックの最上位にハンドルが含まれている場合に発生します。削減するために、POP関数がスタックで実行され、ハンドルが飛び出し、LHS非終端記号に置き換えられます。
LRパーサー
LRパーサーは、非再帰的なシフトリデュースのボトムアップパーサーです。幅広いクラスの文脈自由文法を使用しているため、最も効率的な構文解析手法になります。LRパーサーはLR(k)パーサーとも呼ばれ、Lは入力ストリームの左から右へのスキャンを表します。Rは逆の右端の派生の構築を表し、kは決定を行うための先読み記号の数を示します。
LRパーサーを構築するために利用できる3つの広く使用されているアルゴリズムがあります。
- SLR(1)–単純LRパーサー:
- 最小クラスの文法で動作します
- 州の数が少ないため、テーブルが非常に小さい
- シンプルで速い構造
- LR(1)– LRパーサー:
- LR(1)文法の完全なセットで動作します
- 大きなテーブルと多数の状態を生成します
- 遅い建設
- LALR(1)–先読みLRパーサー:
- 文法の中間サイズで動作します
- 状態の数はSLR(1)と同じです
LR解析アルゴリズム
ここでは、LRパーサーのスケルトンアルゴリズムについて説明します。
token = next_token()
repeat forever
s = top of stack
if action[s, token] = “shift si” then
PUSH token
PUSH si
token = next_token()
else if action[s, tpken] = “reduce A::= β“ then
POP 2 * |β| symbols
s = top of stack
PUSH A
PUSH goto[s,A]
else if action[s, token] = “accept” then
return
else
error()LL対LR
| LL | LR |
|---|---|
| 左端の派生を行います。 | 逆に右端の派生を行います。 |
| スタック上の非終端記号のルートから開始します。 | スタック上の非終端記号のルートで終了します。 |
| スタックが空になると終了します。 | 空のスタックから始まります。 |
| スタックを使用して、まだ期待されるものを指定します。 | スタックを使用して、すでに表示されているものを指定します。 |
| 解析ツリーをトップダウンで構築します。 | 解析ツリーをボトムアップで構築します。 |
| 非終端記号をスタックから継続的にポップし、対応する右側を押します。 | スタックの右側を認識しようとし、それをポップして、対応する非終端記号をプッシュします。 |
| 非終端記号を展開します。 | 非終端記号を減らします。 |
| スタックから1つポップすると、端子を読み取ります。 | 端子をスタックにプッシュしながら読み取ります。 |
| 解析ツリーのトラバーサルを事前注文します。 | 解析ツリーのポストオーダートラバーサル。 |
ソースコードとしてのプログラムは、単なるテキスト(コード、ステートメントなど)のコレクションであり、それを存続させるには、ターゲットマシンでアクションを実行する必要があります。プログラムは、命令を実行するためにメモリリソースを必要とします。プログラムには、実行時に実際のメモリ位置とのマッピングを必要とするプロシージャの名前、識別子などが含まれています。
実行時とは、実行中のプログラムを意味します。ランタイム環境は、システムで実行されているプロセスにサービスを提供するためのソフトウェアライブラリ、環境変数などを含む可能性のあるターゲットマシンの状態です。
ランタイムサポートシステムはパッケージであり、ほとんどが実行可能プログラム自体で生成され、プロセスとランタイム環境の間のプロセス通信を容易にします。プログラムの実行中にメモリの割り当てと割り当て解除を処理します。
アクティベーションツリー
プログラムは、いくつかの手順に組み合わされた一連の命令です。プロシージャ内の命令は順番に実行されます。プロシージャには開始区切り文字と終了区切り文字があり、その中のすべてがプロシージャの本体と呼ばれます。プロシージャ識別子とその中の有限命令のシーケンスは、プロシージャの本体を構成します。
プロシージャの実行は、そのアクティブ化と呼ばれます。アクティベーションレコードには、プロシージャを呼び出すために必要なすべての情報が含まれています。アクティベーションレコードには、次の単位が含まれる場合があります(使用されるソース言語によって異なります)。
| 一時的 | 式の一時値と中間値を格納します。 |
| ローカルデータ | 呼び出されたプロシージャのローカルデータを格納します。 |
| マシンステータス | プロシージャが呼び出される前に、レジスタ、プログラムカウンタなどのマシンステータスを格納します。 |
| コントロールリンク | 呼び出し元プロシージャのアクティベーションレコードのアドレスを格納します。 |
| アクセスリンク | ローカルスコープ外のデータの情報を格納します。 |
| 実際のパラメータ | 実際のパラメータ、つまり、呼び出されたプロシージャに入力を送信するために使用されるパラメータを格納します。 |
| 戻り値 | 戻り値を格納します。 |
プロシージャが実行されるたびに、そのアクティブ化レコードはスタック(制御スタックとも呼ばれます)に格納されます。プロシージャが別のプロシージャを呼び出すと、呼び出されたプロシージャが実行を終了するまで、呼び出し元の実行が一時停止されます。このとき、呼び出されたプロシージャのアクティベーションレコードはスタックに保存されます。
プログラム制御はシーケンシャルに流れ、プロシージャが呼び出されると、その制御は呼び出されたプロシージャに移されると想定しています。呼び出されたプロシージャが実行されると、制御が呼び出し元に戻ります。このタイプの制御フローにより、一連のアクティベーションをツリーの形式で簡単に表すことができます。activation tree。
この概念を理解するために、例としてコードを取り上げます。
. . .
printf(“Enter Your Name: “);
scanf(“%s”, username);
show_data(username);
printf(“Press any key to continue…”);
. . .
int show_data(char *user)
{
printf(“Your name is %s”, username);
return 0;
}
. . .以下は、与えられたコードのアクティベーションツリーです。

これで、プロシージャが深さ優先方式で実行されることがわかりました。したがって、スタック割り当ては、プロシージャのアクティブ化に最適なストレージの形式です。
ストレージの割り当て
ランタイム環境は、次のエンティティのランタイムメモリ要件を管理します。
Code:実行時に変更されないプログラムのテキスト部分として知られています。そのメモリ要件は、コンパイル時にわかっています。
Procedures:テキスト部分は静的ですが、ランダムに呼び出されます。そのため、スタックストレージは、プロシージャの呼び出しとアクティブ化を管理するために使用されます。
Variables:変数は、グローバルまたは定数でない限り、実行時にのみ認識されます。ヒープメモリ割り当てスキームは、実行時の変数のメモリの割り当てと割り当て解除を管理するために使用されます。
静的割り当て
この割り当て方式では、コンパイルデータはメモリ内の固定位置にバインドされ、プログラムの実行時に変更されません。メモリ要件と保存場所は事前にわかっているため、メモリの割り当てと割り当て解除のためのランタイムサポートパッケージは必要ありません。
スタック割り当て
プロシージャコールとそのアクティブ化は、スタックメモリ割り当てによって管理されます。これは後入れ先出し(LIFO)方式で機能し、この割り当て戦略は再帰的なプロシージャ呼び出しに非常に役立ちます。
ヒープ割り当て
プロシージャにローカルな変数は、実行時にのみ割り当ておよび割り当て解除されます。ヒープ割り当ては、メモリを変数に動的に割り当て、変数が不要になったときにそれを要求するために使用されます。
静的に割り当てられたメモリ領域を除いて、スタックメモリとヒープメモリの両方が動的かつ予期せずに拡大および縮小する可能性があります。したがって、システムに一定量のメモリを提供することはできません。
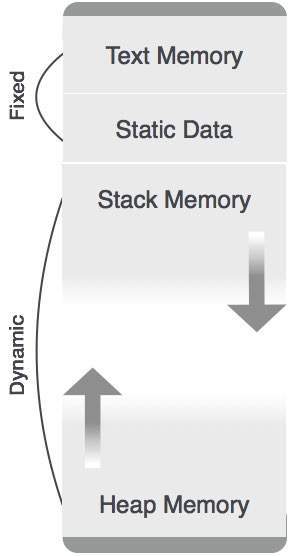
上の画像に示されているように、コードのテキスト部分には一定量のメモリが割り当てられています。スタックメモリとヒープメモリは、プログラムに割り当てられた合計メモリの両端に配置されます。両方が互いに収縮し、成長します。
パラメータの受け渡し
プロシージャ間の通信媒体は、パラメータの受け渡しとして知られています。呼び出し元のプロシージャからの変数の値は、何らかのメカニズムによって呼び出されたプロシージャに転送されます。先に進む前に、まずプログラムの値に関連するいくつかの基本的な用語を確認してください。
r値
式の値は、そのr値と呼ばれます。単一の変数に含まれる値は、代入演算子の右側に表示される場合もr値になります。r値は、いつでも他の変数に割り当てることができます。
l値
式が格納されているメモリ(アドレス)の場所は、その式のl値として知られています。常に代入演算子の左側に表示されます。
例えば:
day = 1;
week = day * 7;
month = 1;
year = month * 12;この例から、1、7、12などの定数値、および日、週、月、年などの変数はすべてr値を持っていることがわかります。変数に割り当てられたメモリ位置も表すため、変数のみにl値があります。
例えば:
7 = x + y;定数7はメモリ位置を表さないため、はl値エラーです。
仮パラメータ
呼び出し元のプロシージャによって渡された情報を受け取る変数は、仮パラメータと呼ばれます。これらの変数は、呼び出された関数の定義で宣言されています。
実際のパラメータ
呼び出されたプロシージャに値またはアドレスが渡される変数は、実パラメータと呼ばれます。これらの変数は、関数呼び出しで引数として指定されます。
Example:
fun_one()
{
int actual_parameter = 10;
call fun_two(int actual_parameter);
}
fun_two(int formal_parameter)
{
print formal_parameter;
}仮パラメーターは、使用されるパラメーター受け渡し手法に応じて、実際のパラメーターの情報を保持します。値またはアドレスの場合があります。
値渡し
値渡しメカニズムでは、呼び出し元のプロシージャーが実パラメーターのr値を渡し、コンパイラーはそれを呼び出されたプロシージャーのアクティブ化レコードに入れます。正式なパラメータは、呼び出し元のプロシージャによって渡された値を保持します。仮パラメータが保持する値が変更されても、実際のパラメータに影響はありません。
参照渡し
パスバイリファレンスメカニズムでは、実際のパラメータのl値が呼び出されたプロシージャのアクティベーションレコードにコピーされます。このようにして、呼び出されたプロシージャは実際のパラメータのアドレス(メモリ位置)を持ち、仮パラメータは同じメモリ位置を参照します。したがって、仮パラメーターが指す値が変更された場合、実際のパラメーターも同じ値を指す必要があるため、実際のパラメーターに影響が見られるはずです。
コピーで渡す-復元
このパラメーター受け渡しメカニズムは、呼び出されたプロシージャーの終了時に実際のパラメーターへの変更が行われることを除いて、「参照渡し」と同様に機能します。関数呼び出し時に、実際のパラメーターの値が、呼び出されたプロシージャーのアクティブ化レコードにコピーされます。操作された場合の仮パラメーターは、実際のパラメーターにリアルタイムの影響を与えません(l値が渡されるため)が、呼び出されたプロシージャーが終了すると、仮パラメーターのl値が実際のパラメーターのl値にコピーされます。
Example:
int y;
calling_procedure()
{
y = 10;
copy_restore(y); //l-value of y is passed
printf y; //prints 99
}
copy_restore(int x)
{
x = 99; // y still has value 10 (unaffected)
y = 0; // y is now 0
}この関数が終了すると、仮パラメーターxのl値が実際のパラメーターyにコピーされます。プロシージャが終了する前にyの値が変更された場合でも、xのl値がyのl値にコピーされ、参照による呼び出しのように動作します。
名前で渡す
Algolのような言語は、C言語のプリプロセッサのように機能する新しい種類のパラメータ受け渡しメカニズムを提供します。名前渡しメカニズムでは、呼び出されるプロシージャの名前が実際の本体に置き換えられます。名前による受け渡しは、プロシージャコール内の引数式を、プロシージャ本体内の対応するパラメータにテキストで置き換えて、参照による受け渡しのように実際のパラメータで機能できるようにします。
シンボルテーブルは、変数名、関数名、オブジェクト、クラス、インターフェイスなどのさまざまなエンティティの出現に関する情報を格納するためにコンパイラによって作成および維持される重要なデータ構造です。シンボルテーブルは、分析と合成の両方で使用されます。コンパイラの一部。
シンボルテーブルは、使用している言語に応じて、次の目的に使用できます。
すべてのエンティティの名前を構造化された形式で1か所に保存します。
変数が宣言されているかどうかを確認します。
型チェックを実装するには、ソースコード内の割り当てと式が意味的に正しいことを確認します。
名前のスコープ(スコープ解像度)を決定します。
シンボルテーブルは、線形テーブルまたはハッシュテーブルのいずれかである単純なテーブルです。次の形式で各名前のエントリを維持します。
<symbol name, type, attribute>たとえば、シンボルテーブルに次の変数宣言に関する情報を格納する必要がある場合:
static int interest;次に、次のようなエントリを保存する必要があります。
<interest, int, static>属性句には、名前に関連するエントリが含まれています。
実装
コンパイラが少量のデータを処理する場合、シンボルテーブルは順序付けられていないリストとして実装できます。これはコーディングが簡単ですが、小さなテーブルにのみ適しています。シンボルテーブルは、次のいずれかの方法で実装できます。
- 線形(ソート済みまたはソートなし)リスト
- 二分探索木
- ハッシュ表
とりわけ、シンボルテーブルは主にハッシュテーブルとして実装され、ソースコードシンボル自体がハッシュ関数のキーとして扱われ、戻り値はシンボルに関する情報です。
操作
線形またはハッシュのシンボルテーブルは、次の操作を提供する必要があります。
インサート()
この操作は、分析フェーズ、つまり、トークンが識別され、名前がテーブルに格納されるコンパイラの前半でより頻繁に使用されます。この操作は、ソースコードで発生する一意の名前に関する情報をシンボルテーブルに追加するために使用されます。名前が格納される形式または構造は、使用しているコンパイラによって異なります。
ソースコード内のシンボルの属性は、そのシンボルに関連付けられている情報です。この情報には、シンボルに関する値、状態、スコープ、およびタイプが含まれています。insert()関数は、シンボルとその属性を引数として受け取り、その情報をシンボルテーブルに格納します。
例えば:
int a;コンパイラは次のように処理する必要があります。
insert(a, int);調べる()
lookup()操作を使用して、シンボルテーブル内の名前を検索し、以下を判別します。
- シンボルがテーブルに存在する場合。
- 使用される前に宣言されている場合。
- 名前がスコープで使用されている場合。
- シンボルが初期化されている場合。
- シンボルが複数回宣言された場合。
lookup()関数の形式は、プログラミング言語によって異なります。基本的な形式は次のように一致する必要があります。
lookup(symbol)シンボルがシンボルテーブルに存在しない場合、このメソッドは0(ゼロ)を返します。シンボルがシンボルテーブルに存在する場合、テーブルに格納されている属性を返します。
スコープ管理
コンパイラは、次の2種類のシンボルテーブルを維持します。 global symbol table すべての手順でアクセスでき、 scope symbol tables プログラム内のスコープごとに作成されます。
名前のスコープを決定するために、シンボルテーブルは次の例に示すように階層構造で配置されます。
. . .
int value=10;
void pro_one()
{
int one_1;
int one_2;
{ \
int one_3; |_ inner scope 1
int one_4; |
} /
int one_5;
{ \
int one_6; |_ inner scope 2
int one_7; |
} /
}
void pro_two()
{
int two_1;
int two_2;
{ \
int two_3; |_ inner scope 3
int two_4; |
} /
int two_5;
}
. . .上記のプログラムは、シンボルテーブルの階層構造で表すことができます。

グローバルシンボルテーブルには、1つのグローバル変数(int値)の名前と2つのプロシージャ名が含まれています。これらは、上記のすべての子ノードで使用できる必要があります。pro_oneシンボルテーブル(およびそのすべての子テーブル)に記載されている名前は、pro_twoシンボルおよびその子テーブルでは使用できません。
このシンボルテーブルのデータ構造階層はセマンティックアナライザに格納され、シンボルテーブルで名前を検索する必要がある場合は常に、次のアルゴリズムを使用して検索されます。
最初に、シンボルが現在のスコープ、つまり現在のシンボルテーブルで検索されます。
名前が見つかった場合は検索が完了します。それ以外の場合は、次のようになるまで親シンボルテーブルで検索されます。
名前が見つかったか、グローバルシンボルテーブルで名前が検索されました。
ソースコードをターゲットマシンコードに直接変換できるのに、なぜソースコードを中間コードに変換してからターゲットコードに変換する必要があるのでしょうか。中間コードが必要な理由を見てみましょう。
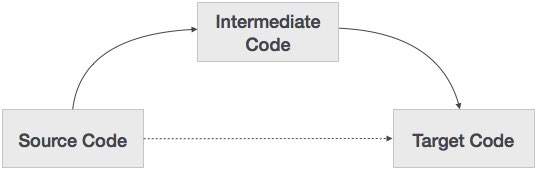
コンパイラが中間コードを生成するオプションを持たずにソース言語をターゲットマシン言語に翻訳する場合、新しいマシンごとに、完全なネイティブコンパイラが必要です。
中間コードは、すべてのコンパイラーで分析部分を同じに保つことにより、すべての固有のマシンに新しい完全なコンパイラーの必要性を排除します。
コンパイラの2番目の部分である合成は、ターゲットマシンに応じて変更されます。
中間コードにコード最適化手法を適用することで、ソースコードの変更を適用してコードのパフォーマンスを向上させることが容易になります。
中間表現
中間コードはさまざまな方法で表すことができ、それぞれに利点があります。
High Level IR-高レベルの中間コード表現は、ソース言語自体に非常に近いものです。これらはソースコードから簡単に生成でき、コードの変更を簡単に適用してパフォーマンスを向上させることができます。ただし、ターゲットマシンの最適化には、あまり好ましくありません。
Low Level IR -これはターゲットマシンに近いため、レジスタとメモリの割り当て、命令セットの選択などに適しています。マシンに依存する最適化に適しています。
中間コードは、言語固有(Javaのバイトコードなど)または言語非依存(3番地コード)のいずれかです。
3番地コード
中間コードジェネレーターは、その前のフェーズであるセマンティックアナライザーから、注釈付きの構文ツリーの形式で入力を受け取ります。次に、その構文木を線形表現、たとえば後置表記に変換できます。中間コードは、マシンに依存しないコードになる傾向があります。したがって、コードジェネレータは、コードを生成するためのメモリストレージ(レジスタ)の数に制限がないことを前提としています。
例えば:
a = b + c * d;中間コードジェネレーターは、この式を部分式に分割してから、対応するコードを生成しようとします。
r1 = c * d;
r2 = b + r1;
a = r2rはターゲットプログラムのレジスタとして使用されます。
3番地コードには、式を計算するための最大3つのアドレス位置があります。3番地コードは、4倍と3倍の2つの形式で表すことができます。
4倍
4重表示の各命令は、演算子、arg1、arg2、および結果の4つのフィールドに分割されます。上記の例は、以下の4つの形式で表されています。
| Op | 引数1 | 引数2 | 結果 |
| * | c | d | r1 |
| + | b | r1 | r2 |
| + | r2 | r1 | r3 |
| = | r3 | a |
トリプル
トリプル表示の各命令には、op、arg1、およびarg2の3つのフィールドがあります。それぞれの部分式の結果は、式の位置で示されます。トリプルは、DAGおよび構文ツリーとの類似性を表します。式を表す場合、これらはDAGと同等です。
| Op | 引数1 | 引数2 |
| * | c | d |
| + | b | (0) |
| + | (1) | (0) |
| = | (2) |
トリプルは、結果が定位置であり、式の順序または位置を変更すると問題が発生する可能性があるため、最適化中にコードが移動できないという問題に直面します。
間接トリプル
この表現は、トリプル表現を拡張したものです。結果を格納するために、位置の代わりにポインタを使用します。これにより、オプティマイザは部分式を自由に再配置して、最適化されたコードを生成できます。
宣言
変数またはプロシージャは、使用する前に宣言する必要があります。宣言には、メモリ内のスペースの割り当てと、シンボルテーブルへのタイプと名前の入力が含まれます。プログラムは、ターゲットマシンの構造を念頭に置いてコーディングおよび設計できますが、ソースコードをターゲット言語に正確に変換できるとは限りません。
プログラム全体をプロシージャとサブプロシージャのコレクションとして使用すると、プロシージャに対してローカルなすべての名前を宣言することが可能になります。メモリの割り当ては連続して行われ、名前はプログラムで宣言された順序でメモリに割り当てられます。オフセット変数を使用して、ベースアドレスを示すゼロ{offset = 0}に設定します。
ソースプログラミング言語とターゲットマシンアーキテクチャは、名前の保存方法が異なる場合があるため、相対アドレス指定が使用されます。名にはメモリ位置0 {offset = 0}からメモリが割り当てられますが、後で宣言される次の名前には、最初の名前の隣にメモリを割り当てる必要があります。
Example:
整数変数に2バイトのメモリが割り当てられ、浮動変数に4バイトのメモリが割り当てられているCプログラミング言語の例を取り上げます。
int a;
float b;
Allocation process:
{offset = 0}
int a;
id.type = int
id.width = 2
offset = offset + id.width
{offset = 2}
float b;
id.type = float
id.width = 4
offset = offset + id.width
{offset = 6}この詳細をシンボルテーブルに入力するには、プロシージャenterを使用できます。このメソッドの構造は次のとおりです。
enter(name, type, offset)このプロシージャは、変数名のシンボルテーブルにエントリを作成し、そのタイプをタイプに設定し、データ領域に相対アドレスオフセットを設定する必要があります。
コード生成は、コンパイルの最終段階と見なすことができます。ポストコード生成を通じて、最適化プロセスをコードに適用できますが、それはコード生成フェーズ自体の一部と見なすことができます。コンパイラによって生成されるコードは、アセンブリ言語などの低レベルプログラミング言語のオブジェクトコードです。高水準言語で記述されたソースコードが低水準言語に変換され、その結果、次の最小プロパティを持つ低水準オブジェクトコードが生成されることを確認しました。
- ソースコードの正確な意味を伝える必要があります。
- CPU使用率とメモリ管理の点で効率的である必要があります。
ここで、中間コードがターゲットオブジェクトコード(この場合はアセンブリコード)にどのように変換されるかを確認します。
有向非巡回グラフ
有向非巡回グラフ(DAG)は、基本ブロックの構造を示し、基本ブロック間を流れる値の流れを確認するのに役立ち、最適化も提供するツールです。DAGは、基本ブロックでの簡単な変換を提供します。DAGはここで理解できます:
リーフノードは、識別子、名前、または定数を表します。
内部ノードは演算子を表します。
内部ノードは、式の結果、または値が格納または割り当てられる識別子/名前も表します。
Example:
t0 = a + b
t1 = t0 + c
d = t0 + t1

[t 0 = a + b] |
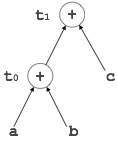
[t 1 = t 0 + c] |
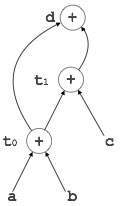
[d = t 0 + t 1 ] |
のぞき穴最適化
この最適化手法は、ソースコードに対してローカルで機能し、ソースコードを最適化されたコードに変換します。ローカルとは、手元にあるコードブロックのごく一部を意味します。これらのメソッドは、ターゲットコードだけでなく中間コードにも適用できます。一連のステートメントが分析され、次の可能な最適化についてチェックされます。
冗長な命令の排除
ソースコードレベルでは、ユーザーは次のことを実行できます。
|
|
|
|
コンパイルレベルでは、コンパイラは本質的に冗長な命令を検索します。命令の複数のロードと保存は、それらの一部が削除された場合でも同じ意味を持つ場合があります。例えば:
- MOV x、R0
- MOV R0、R1
最初の命令を削除して、次のように文を書き直すことができます。
MOV x, R1到達不能なコード
到達不能コードは、プログラミング構造のためにアクセスされることのないプログラムコードの一部です。プログラマーが、到達できないコードを誤って記述した可能性があります。
Example:
void add_ten(int x)
{
return x + 10;
printf(“value of x is %d”, x);
}このコードセグメントでは、 printf プログラムコントロールが実行可能になる前に戻るため、ステートメントは実行されません。 printf 削除することができます。
制御最適化の流れ
プログラムコントロールが重要なタスクを実行せずに前後にジャンプするコード内のインスタンスがあります。これらのジャンプは削除できます。次のコードのチャンクについて考えてみます。
...
MOV R1, R2
GOTO L1
...
L1 : GOTO L2
L2 : INC R1このコードでは、ラベルL1は、制御をL2に渡すときに削除できます。したがって、以下に示すように、L1にジャンプしてからL2にジャンプする代わりに、コントロールはL2に直接到達できます。
...
MOV R1, R2
GOTO L2
...
L2 : INC R1代数式の簡略化
代数式を簡単にできる場合があります。たとえば、式a = a + 0 に置き換えることができます a それ自体と式a = a + 1は、単にINCaに置き換えることができます。
強度低下
より多くの時間とスペースを消費する操作があります。それらの「強度」は、時間とスペースをあまり消費しない他の操作に置き換えることで減らすことができますが、同じ結果が得られます。
例えば、 x * 2 に置き換えることができます x << 1、これには1つの左シフトのみが含まれます。* aと2の出力は同じですが、2の方がはるかに効率的に実装できます。
機械の指示へのアクセス
ターゲットマシンは、特定の操作を非常に効率的に実行する機能を持つことができる、より高度な命令を展開できます。ターゲットコードがこれらの命令に直接対応できる場合、コードの品質が向上するだけでなく、より効率的な結果が得られます。
コードジェネレーター
コードジェネレーターは、ターゲットマシンのランタイム環境とその命令セットを理解している必要があります。コードジェネレーターは、コードを生成するために次のことを考慮に入れる必要があります。
Target language:コードジェネレーターは、コードが変換されるターゲット言語の性質を認識している必要があります。その言語は、コンパイラがより便利な方法でコードを生成するのを助けるために、いくつかのマシン固有の命令を容易にするかもしれません。ターゲットマシンは、CISCまたはRISCプロセッサアーキテクチャのいずれかを持つことができます。
IR Type:中間表現にはさまざまな形式があります。抽象構文木(AST)構造、逆ポーランド記法、または3番地コードにすることができます。
Selection of instruction:コードジェネレーターは、中間表現を入力として受け取り、それをターゲットマシンの命令セットに変換(マップ)します。1つの表現には、それを変換するための多くの方法(命令)があります。そのため、適切な命令を賢く選択するのはコードジェネレーターの責任になります。
Register allocation:プログラムには、実行中に維持される値がいくつかあります。ターゲットマシンのアーキテクチャでは、すべての値をCPUメモリまたはレジスタに保持できない場合があります。コードジェネレータは、レジスタに保持する値を決定します。また、これらの値を保持するために使用するレジスタを決定します。
Ordering of instructions:最後に、コードジェネレーターが命令の実行順序を決定します。それらを実行するための命令のスケジュールを作成します。
記述子
コードジェネレーターは、コードの生成中にレジスター(可用性のため)とアドレス(値の場所)の両方を追跡する必要があります。どちらの場合も、次の2つの記述子が使用されます。
Register descriptor:レジスタ記述子は、レジスタの可用性についてコードジェネレータに通知するために使用されます。レジスタ記述子は、各レジスタに格納されている値を追跡します。コード生成中に新しいレジスタが必要になると、レジスタの可用性についてこの記述子が参照されます。
Address descriptor:プログラムで使用される名前(識別子)の値は、実行中に異なる場所に保存される場合があります。アドレス記述子は、識別子の値が格納されているメモリ位置を追跡するために使用されます。これらの場所には、CPUレジスタ、ヒープ、スタック、メモリ、または上記の場所の組み合わせが含まれる場合があります。
コードジェネレーターは、両方の記述子をリアルタイムで更新し続けます。loadステートメントの場合、LD R1、x、コードジェネレーター:
- xの値を持つRegisterDescriptorR1を更新します。
- アドレス記述子(x)を更新して、xの1つのインスタンスがR1にあることを示します。
コード生成
基本ブロックは、一連の3アドレス命令で構成されます。コードジェネレーターは、これらの一連の命令を入力として受け取ります。
Note:名前の値が複数の場所(レジスタ、キャッシュ、またはメモリ)で見つかった場合、レジスタの値がキャッシュおよびメインメモリよりも優先されます。同様に、キャッシュの値はメインメモリよりも優先されます。メインメモリはほとんど優先されません。
getReg:コードジェネレーターはgetReg関数を使用して、使用可能なレジスターのステータスと名前値の場所を判別します。getRegは次のように機能します。
変数YがすでにレジスタRにある場合は、そのレジスタを使用します。
それ以外の場合、レジスタRが使用可能な場合は、そのレジスタを使用します。
それ以外の場合、上記の両方のオプションが不可能な場合は、最小限のロードおよびストア命令を必要とするレジスタを選択します。
命令x = y OP zの場合、コードジェネレータは次のアクションを実行できます。LがyOP zの出力が保存される場所(できればレジスター)であると仮定します。
関数getRegを呼び出して、Lの場所を決定します。
の現在の場所(レジスタまたはメモリ)を決定します y のアドレス記述子を参照して y。場合y 現在登録されていません L、次に次の命令を生成して、の値をコピーします。 y に L:
MOV y '、L
どこ y’ のコピーされた値を表します y。
の現在の場所を決定します z 手順2で使用したのと同じ方法を使用して y 次の命令を生成します。
OP z '、L
どこ z’ のコピーされた値を表します z。
ここで、Lにはy OP zの値が含まれています。これは、に割り当てられることを目的としています。 x。したがって、Lがレジスタである場合は、記述子を更新して、次の値が含まれていることを示します。x。の記述子を更新しますx 場所に保存されていることを示す L。
yとzがそれ以上使用されない場合は、システムに戻すことができます。
ループや条件文などの他のコード構造は、一般的なアセンブリ方法でアセンブリ言語に変換されます。
最適化は、コードがより少ないリソース(つまり、CPU、メモリ)を消費し、高速を提供することによってコードを改善しようとするプログラム変換手法です。
最適化では、高レベルの一般的なプログラミング構造が非常に効率的な低レベルのプログラミングコードに置き換えられます。コード最適化プロセスは、以下の3つのルールに従う必要があります。
出力コードは、プログラムの意味を変更してはなりません。
最適化によりプログラムの速度が向上し、可能であれば、プログラムが必要とするリソースの数を減らす必要があります。
最適化自体は高速であり、コンパイルプロセス全体を遅らせるべきではありません。
最適化されたコードの取り組みは、プロセスのコンパイルのさまざまなレベルで行うことができます。
最初に、ユーザーはコードを変更/再配置したり、より優れたアルゴリズムを使用してコードを記述したりできます。
中間コードを生成した後、コンパイラはアドレス計算とループの改善によって中間コードを変更できます。
コンパイラは、ターゲットマシンコードを生成するときに、メモリ階層とCPUレジスタを利用できます。
最適化は、マシンに依存しないタイプとマシンに依存するタイプの2つのタイプに大きく分類できます。
マシンに依存しない最適化
この最適化では、コンパイラは中間コードを取り込み、CPUレジスタや絶対メモリ位置を含まないコードの一部を変換します。例えば:
do
{
item = 10;
value = value + item;
}while(value<100);このコードには、識別子アイテムの繰り返しの割り当てが含まれます。このようにすると、次のようになります。
Item = 10;
do
{
value = value + item;
} while(value<100);CPUサイクルを節約するだけでなく、どのプロセッサでも使用できます。
機械依存の最適化
マシン依存の最適化は、ターゲットコードが生成された後、ターゲットマシンアーキテクチャに従ってコードが変換されたときに実行されます。これにはCPUレジスタが含まれ、相対参照ではなく絶対メモリ参照がある場合があります。マシン依存のオプティマイザは、メモリ階層を最大限に活用するように努めています。
基本ブロック
ソースコードには通常、いくつかの命令があり、それらは常に順番に実行され、コードの基本ブロックと見なされます。これらの基本ブロックにはジャンプステートメントがありません。つまり、最初の命令が実行されると、同じ基本ブロック内のすべての命令が、プログラムのフロー制御を失うことなく、出現順に実行されます。
プログラムは、IF-THEN-ELSE、SWITCH-CASE条件ステートメント、DO-WHILE、FOR、REPEAT-UNTILなどのループなどの基本ブロックとしてさまざまな構造を持つことができます。
基本ブロックの識別
次のアルゴリズムを使用して、プログラム内の基本ブロックを見つけることができます。
基本ブロックが開始するすべての基本ブロックのヘッダーステートメントを検索します。
- プログラムの最初のステートメント。
- 任意のブランチのターゲットとなるステートメント(条件付き/無条件)。
- 分岐ステートメントに続くステートメント。
ヘッダーステートメントとそれに続くステートメントは、基本ブロックを形成します。
基本ブロックには、他の基本ブロックのヘッダーステートメントは含まれていません。
基本ブロックは、コード生成と最適化の両方の観点から重要な概念です。
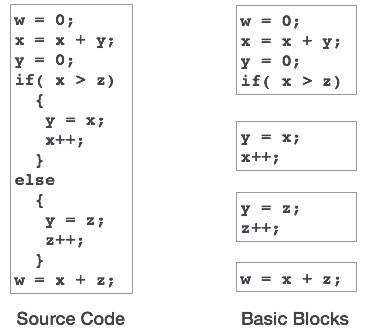
基本ブロックは、単一の基本ブロックで複数回使用されている変数を識別する際に重要な役割を果たします。いずれかの変数が複数回使用されている場合、ブロックの実行が終了しない限り、その変数に割り当てられているレジスタメモリを空にする必要はありません。
制御フローグラフ
プログラムの基本ブロックは、制御フローグラフを使用して表すことができます。制御フローグラフは、プログラム制御がブロック間でどのように渡されるかを示しています。これは、プログラム内の不要なループを見つけるのに役立つ最適化に役立つ便利なツールです。
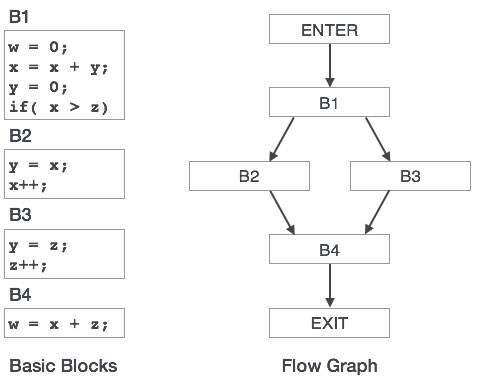
ループ最適化
ほとんどのプログラムは、システム内でループとして実行されます。CPUサイクルとメモリを節約するために、ループを最適化する必要があります。ループは、次の手法で最適化できます。
Invariant code:ループ内に存在し、各反復で同じ値を計算するコードのフラグメントは、ループ不変コードと呼ばれます。このコードは、反復ごとではなく1回だけ計算されるように保存することで、ループの外に移動できます。
Induction analysis :変数の値がループ内でループ不変値によって変更される場合、その変数は帰納変数と呼ばれます。
Strength reduction:より多くのCPUサイクル、時間、およびメモリを消費する式があります。これらの式は、式の出力を損なうことなく、より安価な式に置き換える必要があります。たとえば、乗算(x * 2)はCPUサイクルの点で(x << 1)よりもコストがかかり、同じ結果が得られます。
デッドコードの除去
デッドコードは、次の1つまたは複数のコードステートメントです。
- 実行されなかったか、到達不能のいずれか、
- または、実行された場合、それらの出力は使用されません。
したがって、デッドコードはどのプログラム操作でも何の役割も果たさないため、簡単に排除できます。
部分的にデッドコード
計算値が特定の状況でのみ使用されるコードステートメントがいくつかあります。つまり、値が使用される場合と使用されない場合があります。このようなコードは、部分的なデッドコードとして知られています。
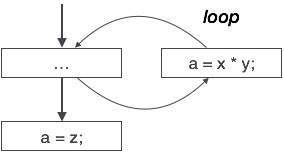
上記の制御フローグラフは、変数「a」を使用して式「x * y」の出力を割り当てるプログラムのチャンクを示しています。'a'に割り当てられた値がループ内で使用されることはないと仮定します。コントロールがループを離れた直後に、 'a'には変数 'z'の値が割り当てられ、プログラムの後半で使用されます。ここで、「a」の割り当てコードはどこでも使用されないため、削除する資格があると結論付けます。
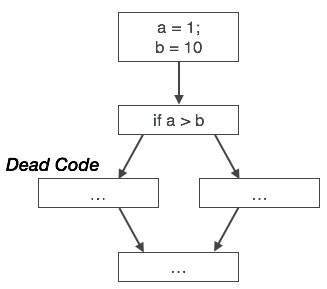
同様に、上の図は、条件ステートメントが常にfalseであることを示しています。これは、真の場合に記述されたコードが実行されることはないため、削除できることを意味します。
部分的な冗長性
冗長式は、オペランドを変更せずに並列パスで複数回計算されますが、部分冗長式は、オペランドを変更せずにパスで複数回計算されます。例えば、
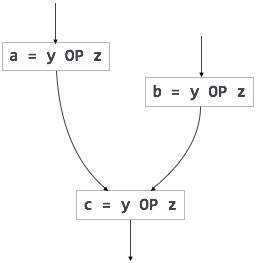
【冗長表現】 |
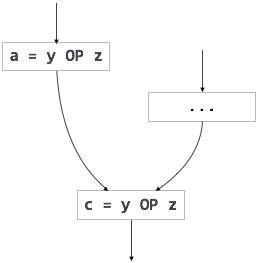
【部分的に冗長な表現】 |
ループ不変コードは部分的に冗長であり、コードモーション手法を使用することで排除できます。
部分的に冗長なコードの別の例は次のとおりです。
If (condition)
{
a = y OP z;
}
else
{
...
}
c = y OP z;オペランドの値(y そして z)変数の割り当てから変更されません a 変数に c。ここで、条件ステートメントが真の場合、y OP zは2回計算され、それ以外の場合は1回計算されます。以下に示すように、コードモーションを使用して、この冗長性を排除できます。
If (condition)
{
...
tmp = y OP z;
a = tmp;
...
}
else
{
...
tmp = y OP z;
}
c = tmp;ここで、条件が真か偽か。y OPzは1回だけ計算する必要があります。