公開鍵暗号化

公開鍵暗号

対称鍵暗号とは異なり、公開鍵暗号の歴史的な使用法はありません。これは比較的新しい概念です。

対称暗号化は、政府、軍隊、大手金融会社などの組織が分類された通信に関与する場合に非常に適していました。

過去数十年でより安全でないコンピュータネットワークが普及したため、暗号化をより大規模に使用することが真に必要であると感じられました。対称鍵は、鍵管理で直面した課題のため、実用的ではないことがわかりました。これにより、公開鍵暗号システムが生まれました。

暗号化と復号化のプロセスを次の図に示します-

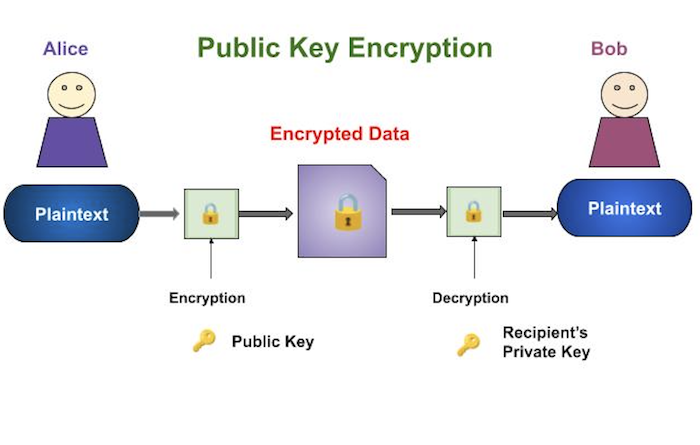
公開鍵暗号化スキームの最も重要なプロパティは次のとおりです。

暗号化と復号化には異なるキーが使用されます。これは、このスキームを対称暗号化スキームとは異なるものに設定するプロパティです。
各受信者は、一般に秘密鍵と呼ばれる一意の復号化鍵を持っています。
受信者は、公開鍵と呼ばれる暗号化鍵を公開する必要があります。
このスキームでは、受信者としての攻撃者によるなりすましを回避するために、公開鍵の信頼性をある程度保証する必要があります。一般に、このタイプの暗号システムには、特定の公開鍵が特定の個人またはエンティティのみに属することを証明する信頼できるサードパーティが含まれます。
暗号化アルゴリズムは、攻撃者が暗号文と暗号化（公開）鍵から平文を推測することを防ぐのに十分複雑です。
秘密鍵と公開鍵は数学的に関連していますが、公開鍵から秘密鍵を計算することはできません。実際、公開鍵暗号システムのインテリジェントな部分は、2つの鍵間の関係を設計することです。

公開鍵暗号化スキームには3つのタイプがあります。次のセクションでそれらについて説明します-

RSA暗号システム

この暗号システムは初期システムの1つです。それは今日でも最も採用されている暗号システムのままです。このシステムは3人の学者によって発明されましたRon Rivest, Adi Shamir, そして Len Adleman したがって、RSA暗号システムと呼ばれます。

RSA暗号システムの2つの側面、1つ目は鍵ペアの生成、2つ目は暗号化-復号化アルゴリズムについて説明します。

RSAキーペアの生成

暗号化を使用した通信への参加を希望する各個人または当事者は、公開鍵と秘密鍵のペアの鍵を生成する必要があります。キーの生成に続くプロセスを以下に説明します-

Generate the RSA modulus (n)
- 2つの大きな素数pとqを選択します。
- n = p * qを計算します。強力な解読不能な暗号化の場合、nを大きな数、通常は最小512ビットとします。
Find Derived Number (e)
- 数 e 1より大きく（p − 1）（q − 1）未満である必要があります。
- eと（p − 1）（q − 1）には、1を除いて共通の因子があってはなりません。言い換えると、2つの数eと（p – 1）（q – 1）は互いに素です。
Form the public key
- 数字のペア（n、e）はRSA公開鍵を形成し、公開されます。
- 興味深いことに、nは公開鍵の一部ですが、大きな素数を因数分解するのが難しいため、攻撃者はnを取得するために使用される2つの素数（pとq）を有限時間で見つけることができません。これがRSAの強みです。
Generate the private key
- 秘密鍵dは、p、q、およびeから計算されます。与えられたnとeに対して、一意の番号dがあります。
- 数dは、eを法とする（p --1）（q – 1）の逆数です。これは、dが（p-1）（q-1）より小さい数であり、eを掛けると、（p-1）（q-1）を法として1に等しくなることを意味します。
- この関係は数学的に次のように書かれています-

ed = 1 mod (p − 1)(q − 1)

拡張ユークリッドアルゴリズムは、p、q、およびeを入力として受け取り、dを出力として与えます。

例

RSAキーペアの生成例を以下に示します。（理解を容易にするために、ここで使用される素数pとqは小さい値です。実際には、これらの値は非常に高くなっています）。

2つの素数をp = 7およびq = 13とします。したがって、モジュラスn = pq = 7 x 13 = 91です。
e = 5を選択します。これは、1を除いて、5の公約数および（p − 1）（q − 1）= 6×12 = 72である数がないため、有効な選択です。
数字のペア（n、e）=（91、5）は公開鍵を形成し、暗号化されたメッセージを送信できるようにしたいすべての人が利用できるようにすることができます。
拡張ユークリッドアルゴリズムにp = 7、q = 13、e = 5を入力します。出力はd = 29になります。
−を計算して、計算されたdが正しいことを確認します。

de = 29 × 5 = 145 = 1 mod 72

したがって、公開鍵は（91、5）であり、秘密鍵は（91、29）です。

暗号化と復号化

キーペアが生成されると、暗号化と復号化のプロセスは比較的簡単で、計算が簡単になります。

興味深いことに、RSAは、対称鍵暗号化の場合のようにビットの文字列を直接操作しません。これは、nを法とする数値で動作します。したがって、平文をn未満の一連の数として表す必要があります。

RSA暗号化

送信者が、公開鍵が（n、e）である誰かにテキストメッセージを送信したいとします。
次に、送信者は平文をn未満の一連の数値として表します。
nを法とする数である最初の平文Pを暗号化すること。暗号化プロセスは、次のような単純な数学的ステップです。

C = P^e mod n

言い換えると、暗号文Cは、平文Pにそれ自体をe回乗算し、nを法として縮小したものに等しくなります。これは、Cもn未満の数であることを意味します。
平文P = 10の鍵生成の例に戻ると、暗号文C −が得られます。

C = 10⁵ mod 91

RSA復号化

RSAの復号化プロセスも非常に簡単です。公開鍵ペア（n、e）の受信者が暗号文Cを受信したとします。
受信者はCを自分の秘密鍵の累乗に上げますd。nを法とする結果は、平文Pになります。

Plaintext = C^d mod n

再び数値例に戻ると、暗号文C = 82は、秘密鍵29 −を使用して番号10に復号化されます。

Plaintext = 82²⁹ mod 91 = 10

RSA分析

RSAのセキュリティは、2つの別個の機能の長所に依存します。RSA暗号システムは、最も人気のある公開鍵暗号システムの強みであり、非常に大きな数を因数分解することの実際的な難しさに基づいています。

Encryption Function −平文を暗号文に変換する一方向性関数と見なされ、秘密鍵の知識がなければ元に戻すことができません。
Key Generation− RSA公開鍵から秘密鍵を決定することの難しさは、モジュラスnを因数分解することと同じです。したがって、攻撃者は、nを因数分解できない限り、RSA公開鍵の知識を使用してRSA秘密鍵を決定することはできません。これは一方向性関数でもあり、p＆q値からモジュラスnに移行するのは簡単ですが、逆にすることはできません。

これらの2つの機能のいずれかが一方向ではないことが証明された場合、RSAは機能しなくなります。実際、効率的に因数分解する手法が開発された場合、RSAは安全ではなくなります。

数pとqが大きな素数でない場合、および/または選択された公開鍵eが小さい数である場合、RSA暗号化の強度は攻撃に対して大幅に低下します。

ElGamal暗号システム

RSAに加えて、他の公開鍵暗号システムが提案されています。それらの多くは、離散対数問題のさまざまなバージョンに基づいています。

楕円曲線バリアントと呼ばれるElGamal暗号システムは、離散対数問題に基づいています。これは、与えられた数の実際の時間枠で離散対数を見つけることができないという仮定から強度を導き出しますが、累乗の逆演算は効率的に計算できます。

pを法とする数で動作するElGamalの単純なバージョンを見てみましょう。楕円曲線の変形の場合、それはまったく異なる数体系に基づいています。

ElGamalキーペアの生成

ElGamal暗号システムの各ユーザーは、次の方法でキーペアを生成します。

Choosing a large prime p. 一般に、1024〜2048ビット長の素数が選択されます。
Choosing a generator element g.
- この数は1からp− 1の間でなければなりませんが、任意の数にすることはできません。
- これは、pを法とする整数の乗法群の生成元です。これは、pと互いに素な整数mごとに、g ^k = a modnとなる整数kが存在することを意味します。
  
  たとえば、3はグループ5の生成元です（Z ₅ = {1、2、3、4}）。

N	3 ⁿ	3 ⁿ mod 5
1	3	3
2	9	4
3	27	2
4	81	1

Choosing the private key. 秘密鍵xは、1より大きくp-1より小さい任意の数です。
Computing part of the public key. 値yは、パラメータp、gおよび秘密鍵xから次のように計算されます。

y = g^x mod p

Obtaining Public key. ElGamal公開鍵は、3つのパラメーター（p、g、y）で構成されています。

たとえば、p = 17およびg = 6であると仮定します（6が群Z _17の生成元であることが確認できます）。秘密鍵xは、1より大きく71より小さい任意の数にすることができるため、x = 5を選択します。値yは、次のように計算されます。

y = 6⁵ mod 17 = 7

したがって、秘密鍵は62で、公開鍵は（17、6、7）です。

暗号化と復号化

ElGamalキーペアの生成は、RSAの同等のプロセスよりも比較的簡単です。ただし、暗号化と復号化はRSAよりも少し複雑です。

ElGamal暗号化

送信者がElGamal公開鍵が（p、g、y）である誰かに平文を送信したいとします。

送信者は、平文をpを法とする一連の数値として表します。
pを法とする数として表される最初の平文Pを暗号化すること。暗号文Cを取得するための暗号化プロセスは次のとおりです。
- 数kをランダムに生成します。
- 2つの値C1とC2を計算します。ここで-

C1 = g^k mod p
C2 = (P^*y^k) mod p

一緒に送信された2つの別々の値（C1、C2）で構成される暗号文Cを送信します。
上記のElGamal鍵生成の例を参照すると、平文P = 13は次のように暗号化されます。
- ランダムに数値を生成します。たとえば、k = 10
- 2つの値C1とC2を計算します。ここで-

C1 = 6¹⁰ mod 17
C2 = (13^*7¹⁰) mod 17 = 9

暗号文C =（C1、C2）=（15、9）を送信します。

ElGamal復号化

秘密鍵xを使用して暗号文（C1、C2）を復号化するには、次の2つの手順を実行します。
- （C1）^x modulo pのモジュラ逆数を計算します。これは（C1）^-xであり、一般に復号化係数と呼ばれます。
- 次の式を使用して平文を取得します-

C2 × (C1)^-x mod p = Plaintext

この例では、秘密鍵x = 5を使用して暗号文C =（C1、C2）=（15、9）を復号化するために、復号化係数は次のようになります。

15^-5 mod 17 = 9

平文を抽出するP =（9×9）mod 17 = 13。

ElGamal分析

ElGamalシステムでは、各ユーザーは秘密鍵xを持っています。と持っていますthree components 公開鍵の prime modulus p, generator g, and public Y = g^x mod p。ElGamalの強さは、離散対数問題の難しさに基づいています。

セキュアキーのサイズは通常> 1024ビットです。今日では、2048ビット長のキーも使用されています。処理速度の面では、Elgamalは非常に遅く、主にキー認証プロトコルに使用されます。処理効率が高いため、ElGamalの楕円曲線バリアントはますます人気が高まっています。

楕円曲線暗号（ECC）

Elliptic Curve Cryptography（ECC）は、離散対数問題の特別なバージョンに基づいてセキュリティが確保される一連の暗号化ツールとプロトコルを説明するために使用される用語です。pを法とする数値は使用しません。

ECCは、楕円曲線と呼ばれる数学的オブジェクトに関連付けられた一連の数値に基づいています。pを法とする数の場合と同様に、これらの数の倍数を加算および計算するための規則があります。

ECCには、ElGamal暗号化やデジタル署名アルゴリズムなどのモジュラー番号用に最初に設計された多くの暗号化スキームのバリエーションが含まれています。

離散対数問題は、楕円曲線上の点に適用するとはるかに難しいと考えられています。これにより、pを法とする数値から楕円曲線上の点への切り替えが促されます。また、楕円曲線ベースのバリアントを使用すると、短いキーで同等のセキュリティレベルを取得できます。

キーが短いと、2つの利点があります-

キー管理のしやすさ
効率的な計算

これらの利点により、暗号化スキームの楕円曲線ベースのバリアントは、コンピューティングリソースが制約されているアプリケーションにとって非常に魅力的です。

RSAおよびElGamalスキーム–比較

さまざまな側面でRSAスキームとElGamalスキームを簡単に比較してみましょう。

RSA	ElGamal
暗号化の方が効率的です。	復号化にはより効率的です。
復号化の効率は低くなります。	復号化にはより効率的です。
特定のセキュリティレベルでは、RSAで長いキーが必要です。	同じレベルのセキュリティを実現するには、非常に短いキーが必要です。
広く受け入れられ、使用されています。	それは新しく、市場ではあまり人気がありません。