遺伝的アルゴリズム-クイックガイド
遺伝的アルゴリズム(GA)は、次の原則に基づく検索ベースの最適化手法です。 Genetics and Natural Selection。これは、解決に一生かかる困難な問題に対する最適またはほぼ最適な解決策を見つけるために頻繁に使用されます。最適化問題の解決、研究、機械学習で頻繁に使用されます。
最適化の概要
最適化はのプロセスです making something better。どのプロセスでも、次の図に示すように、入力のセットと出力のセットがあります。

最適化とは、「最良の」出力値が得られるような方法で入力の値を見つけることです。「最良」の定義は問題ごとに異なりますが、数学的には、入力パラメーターを変更することにより、1つ以上の目的関数を最大化または最小化することを指します。
入力が取ることができるすべての可能なソリューションまたは値のセットは、検索スペースを構成します。この探索空間には、最適解を与える点または点のセットがあります。最適化の目的は、検索空間でそのポイントまたはポイントのセットを見つけることです。
遺伝的アルゴリズムとは何ですか?
自然は常にすべての人類にとって素晴らしいインスピレーションの源でした。遺伝的アルゴリズム(GA)は、自然淘汰と遺伝学の概念に基づく検索ベースのアルゴリズムです。GAは、次のように知られるはるかに大きな計算ブランチのサブセットです。Evolutionary Computation。
GAは、ミシガン大学のJohn Hollandと彼の学生および同僚、特にDavid E. Goldbergによって開発され、それ以来、さまざまな最適化問題で試行され、高い成功を収めています。
GAには、 pool or a population of possible solutions与えられた問題に。次に、これらのソリューションは(自然遺伝学のように)組換えと突然変異を受け、新しい子供を生み出し、このプロセスはさまざまな世代にわたって繰り返されます。各個体(または候補解)には(その目的関数値に基づいて)適応度値が割り当てられ、より適切な個体には、より多くの「より適切な」個体を交配して産出する可能性が高くなります。これは、ダーウィンの「適者生存」の理論と一致しています。
このようにして、私たちは停止基準に達するまで、世代を超えてより良い個人またはソリューションを「進化」させ続けます。
遺伝的アルゴリズムは本質的に十分にランダム化されていますが、履歴情報も活用するため、ランダムローカル検索(さまざまなランダムソリューションを試し、これまでの最良のものを追跡する)よりもはるかに優れたパフォーマンスを発揮します。
GAの利点
GAにはさまざまな利点があり、非常に人気があります。これらには以下が含まれます-
派生情報は必要ありません(多くの実際の問題では利用できない場合があります)。
従来の方法と比較して、より高速で効率的です。
非常に優れた並列機能を備えています。
連続関数と離散関数の両方、および多目的問題を最適化します。
単一のソリューションだけでなく、「優れた」ソリューションのリストを提供します。
問題に対する答えは常に得られますが、時間の経過とともに改善されます。
検索スペースが非常に大きく、関連するパラメーターが多数ある場合に役立ちます。
GAの制限
他の手法と同様に、GAにもいくつかの制限があります。これらには以下が含まれます-
GAは、すべての問題、特に単純で派生情報が利用可能な問題に適しているわけではありません。
適応度の値は繰り返し計算されますが、問題によっては計算コストが高くなる可能性があります。
確率論的であるため、ソリューションの最適性や品質は保証されません。
適切に実装されていない場合、GAは最適解に収束しない可能性があります。
GA –動機
遺伝的アルゴリズムには、「十分な」ソリューションを「十分な速さ」で提供する機能があります。これにより、遺伝的アルゴリズムは最適化問題の解決に使用するのに魅力的です。GAが必要な理由は次のとおりです。
難しい問題の解決
コンピュータサイエンスには、さまざまな問題があります。 NP-Hard。これが本質的に意味することは、最も強力なコンピューティングシステムでさえ、その問題を解決するのに非常に長い時間(さらには数年!)かかるということです。このようなシナリオでは、GAは提供するための効率的なツールであることが証明されていますusable near-optimal solutions 短時間で。
グラジエントベースのメソッドの失敗
従来の微積分ベースの方法は、ランダムなポイントから開始し、丘の頂上に到達するまで勾配の方向に移動することによって機能します。この手法は効率的であり、線形回帰のコスト関数などの単一ピークの目的関数に非常に適しています。しかし、ほとんどの現実の状況では、ランドスケープと呼ばれる非常に複雑な問題があります。ランドスケープは、多くの山と谷で構成されており、局所的な最適点にとらわれるという固有の傾向に悩まされているため、このような方法は失敗します。次の図に示すように。

優れたソリューションを迅速に入手
巡回セールスマン問題(TSP)のようないくつかの難しい問題には、経路探索やVLSI設計などの実際のアプリケーションがあります。ここで、GPSナビゲーションシステムを使用していて、送信元から宛先までの「最適な」パスを計算するのに数分(または数時間)かかると想像してください。このような実際のアプリケーションでの遅延は許容できないため、「高速」で提供される「十分な」ソリューションが必要です。
このセクションでは、GAを理解するために必要な基本的な用語を紹介します。また、GAの一般的な構造は両方で提示されますpseudo-code and graphical forms。読者は、このセクションで紹介されているすべての概念を正しく理解し、このチュートリアルの他のセクションも読むときにそれらを覚えておくことをお勧めします。
基本的な用語
遺伝的アルゴリズムの説明を始める前に、このチュートリアル全体で使用されるいくつかの基本的な用語に精通していることが不可欠です。
Population−これは、特定の問題に対して考えられるすべての(エンコードされた)ソリューションのサブセットです。GAの母集団は、人間の代わりに人間を表す候補ソリューションがあることを除いて、人間の母集団に類似しています。
Chromosomes −染色体は、与えられた問題に対するそのような解決策の1つです。
Gene −遺伝子は染色体の1つの要素の位置です。
Allele −特定の染色体に対して遺伝子がとる値です。
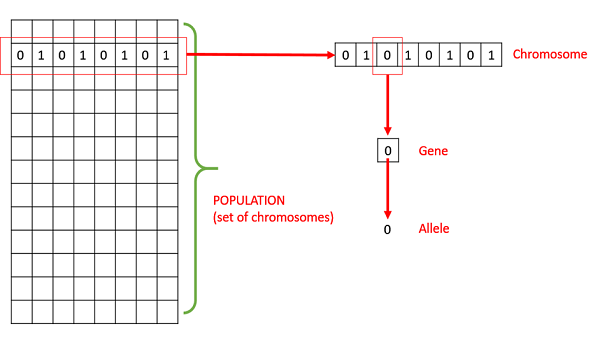
Genotype−遺伝子型は計算空間の母集団です。計算空間では、解は計算システムを使用して簡単に理解および操作できる方法で表されます。
Phenotype −表現型は、実際の現実世界の状況で表現される方法でソリューションが表現される、実際の現実世界のソリューション空間の母集団です。
Decoding and Encoding −単純な問題の場合、 phenotype and genotypeスペースは同じです。ただし、ほとんどの場合、表現型と遺伝子型のスペースは異なります。デコードは、ソリューションを遺伝子型から表現型空間に変換するプロセスであり、エンコードは、表現型から遺伝子型空間に変換するプロセスです。適応度の値の計算中にGAで繰り返し実行されるため、デコードは高速である必要があります。
たとえば、0/1ナップサック問題について考えてみます。表現型スペースは、選択するアイテムのアイテム番号のみを含むソリューションで構成されます。
ただし、遺伝子型空間では、長さnのバイナリ文字列として表すことができます(nはアイテムの数です)。A0 at position x それを表す xthアイテムが選択され、1はその逆を表します。これは、遺伝子型と表現型のスペースが異なる場合です。

Fitness Function−簡単に定義された適応度関数は、解を入力として受け取り、解の適合性を出力として生成する関数です。適応度関数と目的関数が同じである場合もあれば、問題に基づいて異なる場合もあります。
Genetic Operators−これらは子孫の遺伝的構成を変えます。これらには、クロスオーバー、突然変異、選択などが含まれます。
基本構造
GAの基本構造は次のとおりです。
最初の母集団(ランダムに生成されるか、他のヒューリスティックによってシードされる可能性があります)から始め、この母集団から親を選択して交配します。親にクロスオーバーおよび突然変異演算子を適用して、新しい子孫を生成します。そして最後に、これらの子孫が集団内の既存の個体に取って代わり、プロセスが繰り返されます。このようにして、遺伝的アルゴリズムは実際に人類の進化をある程度模倣しようとします。
次の各手順については、このチュートリアルの後半で個別の章として説明します。

GAの一般化された擬似コードは、次のプログラムで説明されています。
GA()
initialize population
find fitness of population
while (termination criteria is reached) do
parent selection
crossover with probability pc
mutation with probability pm
decode and fitness calculation
survivor selection
find best
return best遺伝的アルゴリズムを実装する際に行う最も重要な決定の1つは、ソリューションを表すために使用する表現を決定することです。不適切な表現はGAのパフォーマンスの低下につながる可能性があることが観察されています。
したがって、適切な表現を選択し、表現型と遺伝子型の空間間のマッピングを適切に定義することは、GAの成功に不可欠です。
このセクションでは、遺伝的アルゴリズムで最も一般的に使用される表現のいくつかを紹介します。ただし、表現は非常に問題に固有であり、読者は、ここで言及されている別の表現または表現の組み合わせが自分の問題により適していることに気付く場合があります。
バイナリ表現
これは、GAで最も単純で最も広く使用されている表現の1つです。このタイプの表現では、遺伝子型はビット文字列で構成されます。
解空間がブール決定変数で構成されている場合のいくつかの問題(はいまたはいいえ)では、バイナリ表現は自然です。たとえば、0/1ナップサック問題を考えてみましょう。n個のアイテムがある場合、n個の要素のバイナリ文字列でソリューションを表すことができます。x番目の要素は、アイテムxが選択されているか(1)、選択されていないか(0)を示します。

他の問題、特に数値を扱う問題については、2進表現で数値を表すことができます。この種のエンコーディングの問題は、ビットが異なれば重要性も異なるため、ミューテーションおよびクロスオーバー演算子が望ましくない結果をもたらす可能性があることです。これは、を使用することである程度解決できますGray Coding, 1ビットの変更は、ソリューションに大きな影響を与えないためです。
実数値表現
離散変数ではなく連続変数を使用して遺伝子を定義したい問題の場合、実際の値の表現が最も自然です。ただし、これらの実数値または浮動小数点数の精度はコンピューターに限定されます。

整数表現
離散値遺伝子の場合、解空間を常にバイナリの「yes」または「no」に制限できるとは限りません。たとえば、北、南、東、西の4つの距離をエンコードする場合は、次のようにエンコードできます。{0,1,2,3}。このような場合、整数表現が望ましいです。

順列表現
多くの問題では、解は要素の順序で表されます。このような場合、順列表現が最も適しています。
この表現の典型的な例は、巡回セールスマン問題(TSP)です。この場合、セールスマンはすべての都市のツアーに参加し、各都市を1回だけ訪問して、開始都市に戻る必要があります。ツアーの総距離を最小限に抑える必要があります。このTSPの解決策は、当然、すべての都市の順序付けまたは順列であるため、順列表現を使用することは、この問題に意味があります。

人口は、現世代のソリューションのサブセットです。また、染色体のセットとして定義することもできます。GA人口を扱う際に留意すべき点がいくつかあります-
人口の多様性を維持する必要があります。そうしないと、収束が早まる可能性があります。
GAの速度が低下する可能性があるため、母集団のサイズを大きく維持しないでください。一方、母集団が小さいと、適切な交配プールには不十分な場合があります。したがって、最適な個体数は試行錯誤によって決定する必要があります。
母集団は通常、–の2次元配列として定義されます。 size population, size x, chromosome size。
人口の初期化
GAで母集団を初期化するには、主に2つの方法があります。彼らは-
Random Initialization −初期母集団に完全にランダムな解を入力します。
Heuristic initialization −問題の既知のヒューリスティックを使用して初期母集団を作成します。
母集団全体がヒューリスティックを使用して初期化されるべきではないことが観察されています。これは、母集団が同様のソリューションを持ち、多様性がほとんどない可能性があるためです。ランダム解は、母集団を最適化するためのものであることが実験的に観察されています。したがって、ヒューリスティックな初期化では、母集団全体にヒューリスティックベースのソリューションを入力するのではなく、母集団にいくつかの適切なソリューションをシードし、残りをランダムなソリューションで埋めます。
ヒューリスティックな初期化は、場合によっては母集団の初期の適応度にのみ影響することも観察されていますが、最終的には、最適化につながるのはソリューションの多様性です。
人口モデル
広く使用されている2つの人口モデルがあります-
定常状態
定常状態のGAでは、各反復で1つまたは2つの子孫を生成し、それらが母集団から1つまたは2つの個体を置き換えます。定常状態のGAは、Incremental GA。
世代別
世代モデルでは、「n」個の子孫を生成します。ここで、nは母集団のサイズであり、反復の最後に母集団全体が新しいものに置き換えられます。
簡単に定義された適応度関数は、 candidate solution to the problem as input and produces as output 検討中の問題に関して、ソリューションがどの程度「適切」であるか。
フィットネス値の計算はGAで繰り返し実行されるため、十分に高速である必要があります。適合度値の計算が遅いと、GAに悪影響を及ぼし、非常に遅くなる可能性があります。
ほとんどの場合、適応度関数と目的関数は、目的が特定の目的関数を最大化または最小化することと同じです。ただし、複数の目的と制約を伴うより複雑な問題の場合、Algorithm Designer 別の適応度関数を持つことを選択するかもしれません。
適応度関数は、次の特性を備えている必要があります-
適応度関数は、計算するのに十分高速である必要があります。
特定のソリューションがどの程度適合しているか、または特定のソリューションから個人がどの程度適合しているかを定量的に測定する必要があります。
場合によっては、目前の問題に固有の複雑さのために、適応度関数を直接計算できないことがあります。このような場合、ニーズに合わせて適応度近似を行います。
次の画像は、0/1ナップザックの解の適合度の計算を示しています。これは、選択されているアイテム(1が付いている)の利益値を合計し、ナップザックがいっぱいになるまで要素を左から右にスキャンする単純な適応度関数です。

親の選択は、交配して再結合し、次世代の子孫を作成する親を選択するプロセスです。良い親は個人をより良い、より適切な解決策に駆り立てるので、親の選択はGAの収束率にとって非常に重要です。
ただし、1つの非常に適切なソリューションが数世代で母集団全体を引き継ぐことがないように注意する必要があります。これにより、ソリューションスペース内でソリューションが互いに近くなり、多様性が失われるためです。 Maintaining good diversity人口の中でGAの成功のために非常に重要です。1つの非常に適切なソリューションによる母集団全体のこの占有は、premature convergence GAでは望ましくない状態です。
フィットネスプロポーショナルセレクション
Fitness Proportionate Selectionは、親を選択する最も一般的な方法の1つです。これでは、すべての個人がその適応度に比例する確率で親になることができます。したがって、より適切な個人は、彼らの特徴を次の世代に交配させ、伝播する可能性が高くなります。したがって、そのような選択戦略は、集団内のより適切な個人に選択圧を適用し、時間の経過とともにより良い個人を進化させます。
円形のホイールを考えてみましょう。ホイールはに分かれていますn pies、ここで、nは母集団内の個体数です。各個人は、その適応度の値に比例する円の一部を取得します。
フィットネス比例選択の2つの実装が可能です-
ルーレットホイールセレクション
ルーレットホイールの選択では、円形ホイールは前述のように分割されます。図のようにホイールの円周上で固定点が選択され、ホイールが回転します。固定点の前に来るホイールの領域が親として選択されます。2番目の親についても、同じプロセスが繰り返されます。
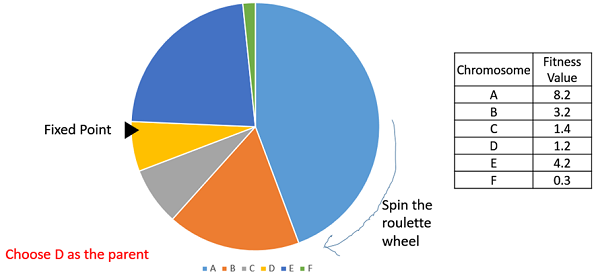
It is clear that a fitter individual has a greater pie on the wheel and therefore a greater chance of landing in front of the fixed point when the wheel is rotated. Therefore, the probability of choosing an individual depends directly on its fitness.
Implementation wise, we use the following steps −
Calculate S = the sum of a finesses.
Generate a random number between 0 and S.
Starting from the top of the population, keep adding the finesses to the partial sum P, till P<S.
The individual for which P exceeds S is the chosen individual.
Stochastic Universal Sampling (SUS)
Stochastic Universal Sampling is quite similar to Roulette wheel selection, however instead of having just one fixed point, we have multiple fixed points as shown in the following image. Therefore, all the parents are chosen in just one spin of the wheel. Also, such a setup encourages the highly fit individuals to be chosen at least once.

It is to be noted that fitness proportionate selection methods don’t work for cases where the fitness can take a negative value.
Tournament Selection
In K-Way tournament selection, we select K individuals from the population at random and select the best out of these to become a parent. The same process is repeated for selecting the next parent. Tournament Selection is also extremely popular in literature as it can even work with negative fitness values.

Rank Selection
Rank Selection also works with negative fitness values and is mostly used when the individuals in the population have very close fitness values (this happens usually at the end of the run). This leads to each individual having an almost equal share of the pie (like in case of fitness proportionate selection) as shown in the following image and hence each individual no matter how fit relative to each other has an approximately same probability of getting selected as a parent. This in turn leads to a loss in the selection pressure towards fitter individuals, making the GA to make poor parent selections in such situations.
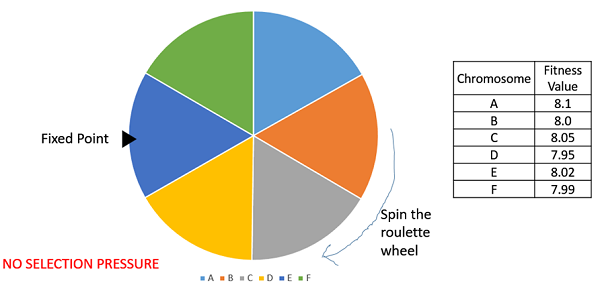
In this, we remove the concept of a fitness value while selecting a parent. However, every individual in the population is ranked according to their fitness. The selection of the parents depends on the rank of each individual and not the fitness. The higher ranked individuals are preferred more than the lower ranked ones.
| Chromosome | Fitness Value | Rank |
|---|---|---|
| A | 8.1 | 1 |
| B | 8.0 | 4 |
| C | 8.05 | 2 |
| D | 7.95 | 6 |
| E | 8.02 | 3 |
| F | 7.99 | 5 |
Random Selection
In this strategy we randomly select parents from the existing population. There is no selection pressure towards fitter individuals and therefore this strategy is usually avoided.
In this chapter, we will discuss about what a Crossover Operator is along with its other modules, their uses and benefits.
Introduction to Crossover
The crossover operator is analogous to reproduction and biological crossover. In this more than one parent is selected and one or more off-springs are produced using the genetic material of the parents. Crossover is usually applied in a GA with a high probability – pc .
Crossover Operators
In this section we will discuss some of the most popularly used crossover operators. It is to be noted that these crossover operators are very generic and the GA Designer might choose to implement a problem-specific crossover operator as well.
One Point Crossover
In this one-point crossover, a random crossover point is selected and the tails of its two parents are swapped to get new off-springs.
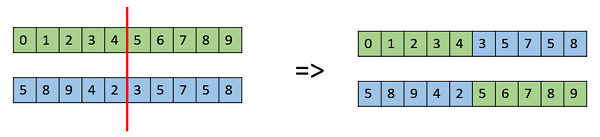
Multi Point Crossover
Multi point crossover is a generalization of the one-point crossover wherein alternating segments are swapped to get new off-springs.

Uniform Crossover
In a uniform crossover, we don’t divide the chromosome into segments, rather we treat each gene separately. In this, we essentially flip a coin for each chromosome to decide whether or not it’ll be included in the off-spring. We can also bias the coin to one parent, to have more genetic material in the child from that parent.

Whole Arithmetic Recombination
This is commonly used for integer representations and works by taking the weighted average of the two parents by using the following formulae −
- Child1 = α.x + (1-α).y
- Child2 = α.x + (1-α).y
Obviously, if α = 0.5, then both the children will be identical as shown in the following image.

Davis’ Order Crossover (OX1)
OX1 is used for permutation based crossovers with the intention of transmitting information about relative ordering to the off-springs. It works as follows −
Create two random crossover points in the parent and copy the segment between them from the first parent to the first offspring.
Now, starting from the second crossover point in the second parent, copy the remaining unused numbers from the second parent to the first child, wrapping around the list.
Repeat for the second child with the parent’s role reversed.

There exist a lot of other crossovers like Partially Mapped Crossover (PMX), Order based crossover (OX2), Shuffle Crossover, Ring Crossover, etc.
Introduction to Mutation
In simple terms, mutation may be defined as a small random tweak in the chromosome, to get a new solution. It is used to maintain and introduce diversity in the genetic population and is usually applied with a low probability – pm. If the probability is very high, the GA gets reduced to a random search.
Mutation is the part of the GA which is related to the “exploration” of the search space. It has been observed that mutation is essential to the convergence of the GA while crossover is not.
Mutation Operators
In this section, we describe some of the most commonly used mutation operators. Like the crossover operators, this is not an exhaustive list and the GA designer might find a combination of these approaches or a problem-specific mutation operator more useful.
Bit Flip Mutation
In this bit flip mutation, we select one or more random bits and flip them. This is used for binary encoded GAs.

Random Resetting
Random Resetting is an extension of the bit flip for the integer representation. In this, a random value from the set of permissible values is assigned to a randomly chosen gene.
Swap Mutation
In swap mutation, we select two positions on the chromosome at random, and interchange the values. This is common in permutation based encodings.

Scramble Mutation
Scramble mutation is also popular with permutation representations. In this, from the entire chromosome, a subset of genes is chosen and their values are scrambled or shuffled randomly.

Inversion Mutation
In inversion mutation, we select a subset of genes like in scramble mutation, but instead of shuffling the subset, we merely invert the entire string in the subset.

The Survivor Selection Policy determines which individuals are to be kicked out and which are to be kept in the next generation. It is crucial as it should ensure that the fitter individuals are not kicked out of the population, while at the same time diversity should be maintained in the population.
Some GAs employ Elitism. In simple terms, it means the current fittest member of the population is always propagated to the next generation. Therefore, under no circumstance can the fittest member of the current population be replaced.
The easiest policy is to kick random members out of the population, but such an approach frequently has convergence issues, therefore the following strategies are widely used.
Age Based Selection
In Age-Based Selection, we don’t have a notion of a fitness. It is based on the premise that each individual is allowed in the population for a finite generation where it is allowed to reproduce, after that, it is kicked out of the population no matter how good its fitness is.
For instance, in the following example, the age is the number of generations for which the individual has been in the population. The oldest members of the population i.e. P4 and P7 are kicked out of the population and the ages of the rest of the members are incremented by one.

Fitness Based Selection
In this fitness based selection, the children tend to replace the least fit individuals in the population. The selection of the least fit individuals may be done using a variation of any of the selection policies described before – tournament selection, fitness proportionate selection, etc.
For example, in the following image, the children replace the least fit individuals P1 and P10 of the population. It is to be noted that since P1 and P9 have the same fitness value, the decision to remove which individual from the population is arbitrary.

The termination condition of a Genetic Algorithm is important in determining when a GA run will end. It has been observed that initially, the GA progresses very fast with better solutions coming in every few iterations, but this tends to saturate in the later stages where the improvements are very small. We usually want a termination condition such that our solution is close to the optimal, at the end of the run.
Usually, we keep one of the following termination conditions −
- When there has been no improvement in the population for X iterations.
- When we reach an absolute number of generations.
- When the objective function value has reached a certain pre-defined value.
For example, in a genetic algorithm we keep a counter which keeps track of the generations for which there has been no improvement in the population. Initially, we set this counter to zero. Each time we don’t generate off-springs which are better than the individuals in the population, we increment the counter.
However, if the fitness any of the off-springs is better, then we reset the counter to zero. The algorithm terminates when the counter reaches a predetermined value.
Like other parameters of a GA, the termination condition is also highly problem specific and the GA designer should try out various options to see what suits his particular problem the best.
Till now in this tutorial, whatever we have discussed corresponds to the Darwinian model of evolution – natural selection and genetic variation through recombination and mutation. In nature, only the information contained in the individual’s genotype can be transmitted to the next generation. This is the approach which we have been following in the tutorial so far.
However, other models of lifetime adaptation – Lamarckian Model and Baldwinian Model also do exist. It is to be noted that whichever model is the best, is open for debate and the results obtained by researchers show that the choice of lifetime adaptation is highly problem specific.
Often, we hybridize a GA with local search – like in Memetic Algorithms. In such cases, one might choose do go with either Lamarckian or Baldwinian Model to decide what to do with individuals generated after the local search.
Lamarckian Model
The Lamarckian Model essentially says that the traits which an individual acquires in his/her lifetime can be passed on to its offspring. It is named after French biologist Jean-Baptiste Lamarck.
Even though, natural biology has completely disregarded Lamarckism as we all know that only the information in the genotype can be transmitted. However, from a computation view point, it has been shown that adopting the Lamarckian model gives good results for some of the problems.
In the Lamarckian model, a local search operator examines the neighborhood (acquiring new traits), and if a better chromosome is found, it becomes the offspring.
Baldwinian Model
The Baldwinian model is an intermediate idea named after James Mark Baldwin (1896). In the Baldwin model, the chromosomes can encode a tendency of learning beneficial behaviors. This means, that unlike the Lamarckian model, we don’t transmit the acquired traits to the next generation, and neither do we completely ignore the acquired traits like in the Darwinian Model.
The Baldwin Model is in the middle of these two extremes, wherein the tendency of an individual to acquire certain traits is encoded rather than the traits themselves.
In this Baldwinian Model, a local search operator examines the neighborhood (acquiring new traits), and if a better chromosome is found, it only assigns the improved fitness to the chromosome and does not modify the chromosome itself. The change in fitness signifies the chromosomes capability to “acquire the trait”, even though it is not passed directly to the future generations.
GAs are very general in nature, and just applying them to any optimization problem wouldn’t give good results. In this section, we describe a few points which would help and assist a GA designer or GA implementer in their work.
Introduce problem-specific domain knowledge
It has been observed that the more problem-specific domain knowledge we incorporate into the GA; the better objective values we get. Adding problem specific information can be done by either using problem specific crossover or mutation operators, custom representations, etc.
The following image shows Michalewicz’s (1990) view of the EA −

Reduce Crowding
Crowding happens when a highly fit chromosome gets to reproduce a lot, and in a few generations, the entire population is filled with similar solutions having similar fitness. This reduces diversity which is a very crucial element to ensure the success of a GA. There are numerous ways to limit crowding. Some of them are −
Mutation to introduce diversity.
Switching to rank selection and tournament selection which have more selection pressure than fitness proportionate selection for individuals with similar fitness.
Fitness Sharing − In this an individual’s fitness is reduced if the population already contains similar individuals.
Randomization Helps!
It has been experimentally observed that the best solutions are driven by randomized chromosomes as they impart diversity to the population. The GA implementer should be careful to keep sufficient amount of randomization and diversity in the population for the best results.
Hybridize GA with Local Search
Local search refers to checking the solutions in the neighborhood of a given solution to look for better objective values.
It may be sometimes useful to hybridize the GA with local search. The following image shows the various places in which local search can be introduced in a GA.

Variation of parameters and techniques
In genetic algorithms, there is no “one size fits all” or a magic formula which works for all problems. Even after the initial GA is ready, it takes a lot of time and effort to play around with the parameters like population size, mutation and crossover probability etc. to find the ones which suit the particular problem.
In this section, we introduce some advanced topics in Genetic Algorithms. A reader looking for just an introduction to GAs may choose to skip this section.
Constrained Optimization Problems
Constrained Optimization Problems are those optimization problems in which we have to maximize or minimize a given objective function value that is subject to certain constraints. Therefore, not all results in the solution space are feasible, and the solution space contains feasible regions as shown in the following image.

In such a scenario, crossover and mutation operators might give us solutions which are infeasible. Therefore, additional mechanisms have to be employed in the GA when dealing with constrained Optimization Problems.
Some of the most common methods are −
Using penalty functions which reduces the fitness of infeasible solutions, preferably so that the fitness is reduced in proportion with the number of constraints violated or the distance from the feasible region.
Using repair functions which take an infeasible solution and modify it so that the violated constraints get satisfied.
Not allowing infeasible solutions to enter into the population at all.
Use a special representation or decoder functions that ensures feasibility of the solutions.
Basic Theoretical Background
In this section, we will discuss about the Schema and NFL theorem along with the building block hypothesis.
Schema Theorem
Researchers have been trying to figure out the mathematics behind the working of genetic algorithms, and Holland’s Schema Theorem is a step in that direction. Over the year’s various improvements and suggestions have been done to the Schema Theorem to make it more general.
In this section, we don’t delve into the mathematics of the Schema Theorem, rather we try to develop a basic understanding of what the Schema Theorem is. The basic terminology to know are as follows −
A Schema is a “template”. Formally, it is a string over the alphabet = {0,1,*},
where * is don’t care and can take any value.
Therefore, *10*1 could mean 01001, 01011, 11001, or 11011
Geometrically, a schema is a hyper-plane in the solution search space.
Order of a schema is the number of specified fixed positions in a gene.

Defining length is the distance between the two furthest fixed symbols in the gene.

The schema theorem states that this schema with above average fitness, short defining length and lower order is more likely to survive crossover and mutation.
Building Block Hypothesis
Building Blocks are low order, low defining length schemata with the above given average fitness. The building block hypothesis says that such building blocks serve as a foundation for the GAs success and adaptation in GAs as it progresses by successively identifying and recombining such “building blocks”.
No Free Lunch (NFL) Theorem
Wolpert and Macready in 1997 published a paper titled "No Free Lunch Theorems for Optimization." It essentially states that if we average over the space of all possible problems, then all non-revisiting black box algorithms will exhibit the same performance.
It means that the more we understand a problem, our GA becomes more problem specific and gives better performance, but it makes up for that by performing poorly for other problems.
GA Based Machine Learning
Genetic Algorithms also find application in Machine Learning. Classifier systems are a form of genetics-based machine learning (GBML) system that are frequently used in the field of machine learning. GBML methods are a niche approach to machine learning.
There are two categories of GBML systems −
The Pittsburg Approach − In this approach, one chromosome encoded one solution, and so fitness is assigned to solutions.
The Michigan Approach − one solution is typically represented by many chromosomes and so fitness is assigned to partial solutions.
It should be kept in mind that the standard issue like crossover, mutation, Lamarckian or Darwinian, etc. are also present in the GBML systems.
Genetic Algorithms are primarily used in optimization problems of various kinds, but they are frequently used in other application areas as well.
In this section, we list some of the areas in which Genetic Algorithms are frequently used. These are −
Optimization − Genetic Algorithms are most commonly used in optimization problems wherein we have to maximize or minimize a given objective function value under a given set of constraints. The approach to solve Optimization problems has been highlighted throughout the tutorial.
Economics − GAs are also used to characterize various economic models like the cobweb model, game theory equilibrium resolution, asset pricing, etc.
Neural Networks − GAs are also used to train neural networks, particularly recurrent neural networks.
Parallelization − GAs also have very good parallel capabilities, and prove to be very effective means in solving certain problems, and also provide a good area for research.
Image Processing − GAs are used for various digital image processing (DIP) tasks as well like dense pixel matching.
Vehicle routing problems − With multiple soft time windows, multiple depots and a heterogeneous fleet.
Scheduling applications − GAs are used to solve various scheduling problems as well, particularly the time tabling problem.
Machine Learning − as already discussed, genetics based machine learning (GBML) is a niche area in machine learning.
Robot Trajectory Generation − GAs have been used to plan the path which a robot arm takes by moving from one point to another.
Parametric Design of Aircraft − GAs have been used to design aircrafts by varying the parameters and evolving better solutions.
DNA Analysis − GAs have been used to determine the structure of DNA using spectrometric data about the sample.
Multimodal Optimization − GAs are obviously very good approaches for multimodal optimization in which we have to find multiple optimum solutions.
Traveling salesman problem and its applications − GAs have been used to solve the TSP, which is a well-known combinatorial problem using novel crossover and packing strategies.
The following books can be referred to further enhance the reader’s knowledge of Genetic Algorithms, and Evolutionary Computation in general −
Genetic Algorithms in Search, Optimization and Machine Learning by David E. Goldberg.
Genetic Algorithms + Data Structures = Evolutionary Programs by Zbigniew Michalewicz.
Practical Genetic Algorithms by Randy L. Haupt and Sue Ellen Haupt.
Multi Objective Optimization using Evolutionary Algorithms by Kalyanmoy Deb.