안테나 이론-포인팅 벡터
안테나는 정보를 전송하거나 수신하기 위해 전자기 에너지를 방출합니다. 따라서 용어Energy 과 Power이 전자기파와 관련이 있으며 우리는 그것들을 논의해야합니다. 전자기파는 전기장과 자기장을 모두 가지고 있습니다.
두 벡터에서 볼 수있는 파동을 고려하십시오. 다음 그림은 전자기파의 전기장 및 자기장 구성 요소를 보여줍니다.
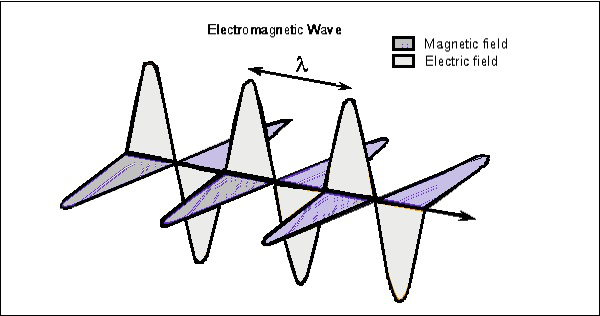
전파는 EM 파의 전파에 수직으로 존재하고 자기 파는 수평으로 위치합니다. 두 필드는 서로 직각을 이룹니다.
포인팅 벡터
포인팅 벡터는 주어진 시간에 단위 면적당 단위 시간당 EM 파의 에너지를 나타냅니다. John Henry Poynting 이 벡터는 1884 년에 처음으로 파생되었으므로 그 이름을 따서 명명되었습니다.
Definition − "Poynting vector는 단위 면적당 에너지 전달률을 나타냅니다."
또는
"파동이 단위 면적당 단위 시간당 운반하는 에너지는 Poynting 벡터에 의해 제공됩니다."
포인팅 벡터는 다음과 같이 표현됩니다. Ŝ.
단위
Poynting 벡터의 SI 단위는 W/m2.
수학적 표현
전자파와 관련된 전력을 설명하는 데 사용되는 양은 순간적입니다. Poynting vector, 이는 다음과 같이 정의됩니다.
$$ \ hat {S} = \ hat {E} \ times \ hat {H} $$어디
$ \ hat {S} $는 순간 포인팅 벡터입니다. (W/m2).
$ \ hat {E} $는 순간 전계 강도입니다. (V/m).
$ \ hat {H} $는 순간 자기장 강도입니다. (A/m).
여기서 주목해야 할 중요한 점은 E의 크기가 EM 파 내에서 H보다 크다는 것입니다. 그러나 둘 다 같은 양의 에너지를 제공합니다. Ŝ는 방향과 크기가 모두있는 벡터입니다. Ŝ의 방향은 파도의 속도와 같습니다. 그 크기는 E와 H에 따라 다릅니다.
포인팅 벡터 유도
Poynting 벡터에 대한 명확한 아이디어를 얻기 위해 단계별 프로세스에서이 Poynting 벡터의 유도를 살펴 보겠습니다.
EM 파동이 파동이 이동하는 X 축에 수직 인 영역 (A)을 통과한다고 상상해 보겠습니다. A를 통과하는 동안 극소 시간 (dt)에서 파동은 거리 (dx)를 이동합니다.
$$ dx = C \ dt $$어디
$$ C = 속도 \ of \ 빛 = 3 \ times 10 ^ {8} m / s $$ $$ volume, dv = Adx = AC \ dt $$ $$ d \ mu = \ mu \ dv = (\ epsilon_ {0} E ^ {2}) (AC \ dt) $$ $$ = \ epsilon_ {0} AC \ E ^ {2} \ dt $$따라서 면적 (A) 당 시간 (dt)으로 전달되는 에너지는-
$$ S = \ frac {에너지} {시간 \ times 면적} = \ frac {dW} {dt \ A} = \ frac {\ epsilon_ {0} ACE ^ {2} \ dt} {dt \ A} = \ 엡실론 _ {0} C \ : E ^ {2} $$이후
$$ \ frac {E} {H} = \ sqrt {\ frac {\ mu_ {0}} {\ epsilon_ {0}}} \ then \ S = \ frac {CB ^ {2}} {\ mu_ {0 }} $$이후
$$ C = \ frac {E} {H} \ 다음 \ S = \ frac {EB} {\ mu_ {0}} $$ $$ = \ hat {S} = \ frac {1} {\ mu_ {0 }} (\ hat {E} \ hat {H}) $$Ŝ Poynting 벡터를 나타냅니다.
위의 방정식은 주어진 시간에 단위 면적당 단위 시간당 에너지를 제공합니다. Poynting vector.