문맥없는 문법 소개
Definition − 유한 한 문법 규칙 집합으로 구성된 CFG (Context-free grammar)는 4 배입니다. (N, T, P, S) 어디
N 비 터미널 기호 세트입니다.
T 터미널 세트입니다. N ∩ T = NULL.
P 일련의 규칙입니다. P: N → (N ∪ T)*즉, 생산 규칙의 왼쪽 P 오른쪽 컨텍스트 또는 왼쪽 컨텍스트가 있습니다.
S 시작 기호입니다.
Example
- 문법 ({A}, {a, b, c}, P, A), P : A → aA, A → abc.
- 문법 ({S, a, b}, {a, b}, P, S), P : S → aSa, S → bSb, S → ε
- 문법 ({S, F}, {0, 1}, P, S), P : S → 00S | 11F, F → 00F | ε
파생 트리 생성
파생 트리 또는 구문 분석 트리는 컨텍스트 프리 문법에서 파생 된 문자열의 의미 정보를 그래픽으로 나타내는 정렬 된 루트 트리입니다.
표현 기법
Root vertex − 시작 기호로 레이블을 지정해야합니다.
Vertex − 비 터미널 기호로 레이블이 지정됩니다.
Leaves − 터미널 기호 또는 ε으로 표시됩니다.
S → x 1 x 2 …… x n 이 CFG의 생산 규칙이면 파스 트리 / 유도 트리는 다음과 같습니다.

파생 트리를 그리는 방법에는 두 가지가 있습니다.
Top-down Approach −
시작 기호로 시작 S
프로덕션을 사용하여 나무 잎으로 내려갑니다.
Bottom-up Approach −
나무 잎에서 시작
시작 기호 인 루트까지 위쪽으로 진행합니다. S
나무의 파생 또는 수확
파스 트리의 파생 또는 산출은 Null을 무시하고 트리 잎의 레이블을 왼쪽에서 오른쪽으로 연결하여 얻은 최종 문자열입니다. 그러나 모든 잎이 Null이면 파생은 Null입니다.
Example
CFG {N, T, P, S}를
N = {S}, T = {a, b}, 시작 기호 = S, P = S → SS | aSb | ε
위의 CFG에서 파생 된 하나는 "abaabb"입니다.
S → SS → aSbS → abS → abaSb → abaaSbb → abaabb

문장 양식 및 부분 파생 트리
부분 파생 트리는 파생 트리 / 구문 분석 트리의 하위 트리로 모든 하위 트리에 하위 트리에 있거나 하위 트리에 아무것도 없습니다.
Example
CFG에서 제작물이-
S → AB, A → aaA | ε, B → Bb | ε
부분 파생 트리는 다음과 같습니다.
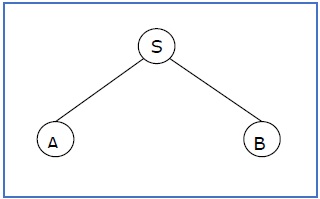
부분 파생 트리에 루트 S가 포함 된 경우이를 sentential form. 위의 하위 트리도 감각적 형식입니다.
문자열의 맨 왼쪽 및 맨 오른쪽 파생
Leftmost derivation − 각 단계에서 가장 왼쪽의 변수에 생산을 적용하여 가장 왼쪽의 도출을 얻습니다.
Rightmost derivation − 각 단계에서 가장 오른쪽 변수에 생산을 적용하여 가장 오른쪽에 파생 된 값을 얻습니다.
Example
CFG의 모든 생산 규칙 세트를
X → X + X | X * X | X | ㅏ
알파벳 {a} 이상.
문자열의 가장 왼쪽 파생 "a+a*a" 아마도-
X → X + X → a + X → a + X * X → a + a * X → a + a * a
위 문자열의 단계적 파생은 다음과 같습니다.

위의 문자열에 대한 가장 오른쪽 파생 "a+a*a" 아마도-
X → X * X → X * a → X + X * a → X + a * a → a + a * a
위 문자열의 단계적 파생은 다음과 같습니다.

왼쪽 및 오른쪽 재귀 문법
문맥없는 문법 G, 형태로 제작이있는 경우 X → Xa 어디 X 비 터미널이고 ‘a’ 터미널의 문자열이며, left recursive production. 왼쪽 재귀 생성을 갖는 문법을left recursive grammar.
그리고 문맥없는 문법에서 G, 생산이있는 경우 형태로 X → aX 어디 X 비 터미널이고 ‘a’ 터미널의 문자열이며, right recursive production. 올바른 재귀 생성을 갖는 문법을right recursive grammar.