공개 키 암호화
공개 키 암호화
대칭 키 암호화와 달리 공개 키 암호화의 과거 사용을 찾을 수 없습니다. 비교적 새로운 개념입니다.
대칭 암호화는 정부, 군대 및 대기업과 같은 조직에 매우 적합했으며 기밀 통신에 참여한 대기업이있었습니다.
지난 수십 년 동안 더 안전하지 않은 컴퓨터 네트워크가 확산됨에 따라 더 큰 규모로 암호화를 사용해야하는 진정한 필요성이 느껴졌습니다. 대칭 키는 키 관리에 직면 한 문제로 인해 실용적이지 않은 것으로 확인되었습니다. 이것은 공개 키 암호 시스템을 발생 시켰습니다.
암호화 및 해독 과정은 다음 그림에 나와 있습니다.
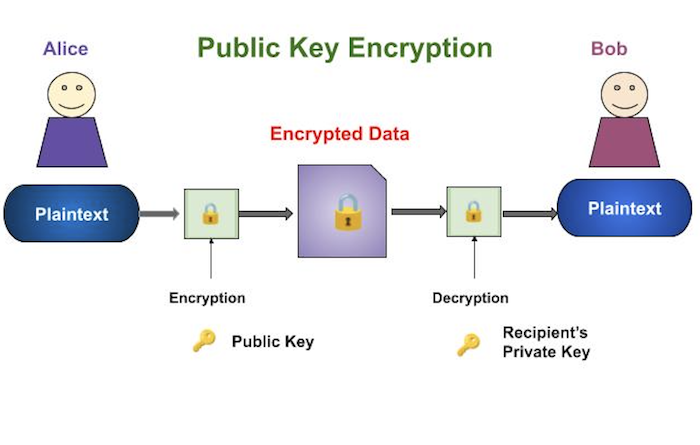
공개 키 암호화 체계의 가장 중요한 속성은 다음과 같습니다.
암호화 및 암호 해독에 다른 키가 사용됩니다. 대칭 암호화 방식과 다른 방식을 설정하는 속성입니다.
각 수신자는 일반적으로 개인 키라고하는 고유 한 암호 해독 키를 가지고 있습니다.
수신자는 공개 키라고하는 암호화 키를 게시해야합니다.
이 체계에서는 수신자로서의 적의 스푸핑을 방지하기 위해 공개 키의 신뢰성에 대한 어느 정도의 보증이 필요합니다. 일반적으로 이러한 유형의 암호화 시스템에는 특정 공개 키가 특정 개인 또는 엔티티에만 속함을 인증하는 신뢰할 수있는 제 3자가 포함됩니다.
암호화 알고리즘은 공격자가 암호문과 암호화 (공개) 키에서 일반 텍스트를 추론하지 못하도록 충분히 복잡합니다.
개인 키와 공개 키는 수학적으로 관련되어 있지만 공개 키에서 개인 키를 계산하는 것은 불가능합니다. 실제로 공개 키 암호화 시스템의 지능적인 부분은 두 키 간의 관계를 설계하는 데 있습니다.
공개 키 암호화 체계에는 세 가지 유형이 있습니다. 다음 섹션에서 논의합니다.
RSA 암호화 시스템
이 암호 시스템은 초기 시스템 중 하나입니다. 오늘날에도 가장 많이 사용되는 암호화 시스템입니다. 이 시스템은 세 학자에 의해 발명되었습니다.Ron Rivest, Adi Shamir, 과 Len Adleman 따라서 RSA 암호 시스템이라고합니다.
우리는 RSA 암호화 시스템의 두 가지 측면, 즉 키 쌍의 첫 번째 생성과 두 번째 암호화-복호화 알고리즘을 볼 것입니다.
RSA 키 쌍 생성
암호화를 사용하여 통신에 참여하려는 각 개인 또는 당사자는 한 쌍의 키, 즉 공개 키와 개인 키를 생성해야합니다. 키 생성 과정은 다음과 같습니다.
Generate the RSA modulus (n)
두 개의 큰 소수, p와 q를 선택합니다.
n = p * q를 계산합니다. 강력한 깨지지 않는 암호화의 경우 n을 큰 수 (일반적으로 최소 512 비트)로 지정합니다.
Find Derived Number (e)
번호 e 1보다 크고 (p − 1) (q − 1)보다 작아야합니다.
1을 제외하고 e와 (p-1) (q-1)에 대한 공약수는 없어야합니다. 즉, 두 개의 숫자 e와 (p-1) (q-1)은 coprime입니다.
Form the public key
숫자 쌍 (n, e)은 RSA 공개 키를 형성하고 공개됩니다.
흥미롭게도 n은 공개 키의 일부이지만 큰 소수를 분해하기 어렵 기 때문에 공격자가 n을 얻는 데 사용 된 두 소수 (p & q)를 유한 한 시간 내에 찾을 수 없습니다. 이것이 RSA의 강점입니다.
Generate the private key
개인 키 d는 p, q 및 e에서 계산됩니다. n과 e가 주어지면 고유 번호 d가 있습니다.
숫자 d는 e 모듈로 (p-1) (q-1)의 역입니다. 즉, d는 (p-1) (q-1)보다 작은 숫자이므로 e를 곱하면 1 모듈로 (p-1) (q-1)와 같습니다.
이 관계는 다음과 같이 수학적으로 작성됩니다.
ed = 1 mod (p − 1)(q − 1)확장 유클리드 알고리즘은 p, q, e를 입력으로 사용하고 d를 출력으로 제공합니다.
예
RSA 키 쌍을 생성하는 예는 다음과 같습니다. (이해의 편의를 위해 여기에서 취한 소수 p & q는 작은 값입니다. 실제로이 값은 매우 높습니다).
두 개의 소수를 p = 7과 q = 13이라고합시다. 따라서 계수 n = pq = 7 x 13 = 91입니다.
e = 5를 선택합니다. 이는 1을 제외하고 5의 공약수 및 (p − 1) (q − 1) = 6 × 12 = 72 인 숫자가 없기 때문에 유효한 선택입니다.
숫자 쌍 (n, e) = (91, 5)는 공개 키를 형성하며 암호화 된 메시지를 보내길 원하는 모든 사람이 사용할 수 있습니다.
확장 유클리드 알고리즘에 p = 7, q = 13 및 e = 5를 입력합니다. 출력은 d = 29입니다.
계산 된 d가 올바른지 확인하십시오-
de = 29 × 5 = 145 = 1 mod 72따라서 공개 키는 (91, 5)이고 개인 키는 (91, 29)입니다.
암호화 및 복호화
키 쌍이 생성되면 암호화 및 복호화 프로세스가 상대적으로 간단하고 계산적으로 쉽습니다.
흥미롭게도 RSA는 대칭 키 암호화의 경우와 같이 비트 문자열에서 직접 작동하지 않습니다. n 모듈로 숫자에서 작동합니다. 따라서 일반 텍스트를 n보다 작은 일련의 숫자로 표현해야합니다.
RSA 암호화
보낸 사람이 공개 키가 (n, e) 인 사람에게 문자 메시지를 보내려고한다고 가정합니다.
그런 다음 보낸 사람은 일반 텍스트를 n보다 작은 일련의 숫자로 나타냅니다.
n 모듈로 숫자 인 첫 번째 일반 텍스트 P를 암호화합니다. 암호화 프로세스는 다음과 같이 간단한 수학적 단계입니다.
C = Pe mod n즉, 암호문 C는 일반 텍스트 P에 e를 곱한 다음 모듈로 n을 줄인 것과 같습니다. 이것은 C도 n보다 작은 숫자임을 의미합니다.
일반 텍스트 P = 10 인 키 생성 예제로 돌아가서 암호문 C를 얻습니다.
C = 105 mod 91RSA 복호화
RSA의 암호 해독 프로세스도 매우 간단합니다. 공개 키 쌍 (n, e)의 수신자가 암호문 C를 수신했다고 가정합니다.
수신자는 C를 개인 키의 힘으로 올립니다. d. 결과 모듈로 n은 일반 텍스트 P가됩니다.
Plaintext = Cd mod n다시 숫자 예제로 돌아 가면 암호문 C = 82는 개인 키 29를 사용하여 숫자 10으로 해독됩니다.
Plaintext = 8229 mod 91 = 10RSA 분석
RSA의 보안은 두 가지 개별 기능의 강점에 따라 달라집니다. RSA 암호화 시스템은 가장 많이 사용되는 공개 키 암호화 시스템의 강점으로 매우 많은 수를 고려하는 실질적인 어려움을 기반으로합니다.
Encryption Function − 평문을 암호문으로 변환하는 단방향 기능으로 간주되며 개인 키 d를 알고 있어야만 되돌릴 수 있습니다.
Key Generation− RSA 공개 키에서 개인 키를 결정하는 것은 계수 n을 인수 분해하는 것과 같습니다. 따라서 공격자는 n을 인수 할 수없는 경우 RSA 공개 키에 대한 지식을 사용하여 RSA 개인 키를 결정할 수 없습니다. 또한 단방향 함수이며 p & q 값에서 계수 n으로 이동하는 것은 쉽지만 역방향은 불가능합니다.
이 두 기능 중 하나가 단방향이 아닌 것으로 판명되면 RSA가 중단됩니다. 사실, 효율적으로 분해하는 기술이 개발되면 RSA는 더 이상 안전하지 않습니다.
RSA 암호화의 강도는 숫자 p와 q가 큰 소수가 아니고 / 또는 선택한 공개 키 e가 작은 숫자 일 경우 공격에 대해 크게 떨어집니다.
ElGamal 암호화 시스템
RSA와 함께 제안 된 다른 공개 키 암호화 시스템이 있습니다. 그들 중 다수는 이산 로그 문제의 다른 버전을 기반으로합니다.
Elliptic Curve Variant라고하는 ElGamal 암호화 시스템은 Discrete Logarithm Problem을 기반으로합니다. 주어진 숫자에 대한 실제 시간 프레임에서 이산 로그를 찾을 수 없다는 가정에서 힘을 도출하는 반면, 거듭 제곱의 역 연산은 효율적으로 계산할 수 있습니다.
모듈로 p로 작동하는 ElGamal의 간단한 버전을 살펴 보겠습니다. 타원 곡선 변형의 경우 상당히 다른 수 체계를 기반으로합니다.
ElGamal 키 쌍 생성
ElGamal 암호 시스템의 각 사용자는 다음과 같이 키 쌍을 생성합니다.
Choosing a large prime p. 일반적으로 1024 ~ 2048 비트 길이의 소수가 선택됩니다.
Choosing a generator element g.
이 숫자는 1과 p-1 사이 여야하지만 어떤 숫자도 될 수 없습니다.
p 모듈로 정수의 곱셈 그룹 생성기입니다. 이것은 모든 정수 m co-prime에서 p까지, g k = a mod n 이되는 정수 k가 있음을 의미합니다 .
예를 들어, 3은 그룹 5의 생성자입니다 (Z 5 = {1, 2, 3, 4}).
| 엔 | 3 N | 3 N은 5 개조 |
|---|---|---|
| 1 | 삼 | 삼 |
| 2 | 9 | 4 |
| 삼 | 27 | 2 |
| 4 | 81 | 1 |
Choosing the private key. 개인 키 x는 1보다 크고 p-1보다 작은 숫자입니다.
Computing part of the public key. 값 y는 다음과 같이 매개 변수 p, g 및 개인 키 x에서 계산됩니다.
y = gx mod pObtaining Public key. ElGamal 공개 키는 세 가지 매개 변수 (p, g, y)로 구성됩니다.
예를 들어, p = 17이고 g = 6이라고 가정합니다 (6이 Z 17 그룹의 생성자임을 확인할 수 있음 ). 개인 키 x는 1보다 크고 71보다 작은 숫자 일 수 있으므로 x = 5를 선택합니다. 그러면 값 y는 다음과 같이 계산됩니다.
y = 65 mod 17 = 7따라서 개인 키는 62이고 공개 키는 (17, 6, 7)입니다.
암호화 및 복호화
ElGamal 키 쌍의 생성은 RSA의 동등한 프로세스보다 비교적 간단합니다. 그러나 암호화 및 암호 해독은 RSA보다 약간 더 복잡합니다.
ElGamal 암호화
보낸 사람이 ElGamal 공개 키가 (p, g, y) 인 사람에게 일반 텍스트를 보내길 원한다고 가정합니다.
보낸 사람은 일반 텍스트를 모듈로 p의 일련의 숫자로 나타냅니다.
모듈로 p로 표시되는 첫 번째 일반 텍스트 P를 암호화합니다. 암호문 C를 얻기위한 암호화 프로세스는 다음과 같습니다.
- 숫자 k를 무작위로 생성합니다.
- 두 값 C1과 C2를 계산합니다.
C1 = gk mod p
C2 = (P*yk) mod p두 개의 개별 값 (C1, C2)으로 구성된 암호문 C를 함께 전송합니다.
위에 주어진 ElGamal 키 생성 예제를 참조하면 일반 텍스트 P = 13은 다음과 같이 암호화됩니다.
- 무작위로 숫자 생성, 예를 들어 k = 10
- 두 값 C1과 C2를 계산합니다.
C1 = 610 mod 17
C2 = (13*710) mod 17 = 9암호문 C = (C1, C2) = (15, 9)를 보냅니다.
ElGamal 복호화
개인 키 x를 사용하여 암호문 (C1, C2)을 해독하려면 다음 두 단계를 수행합니다.
(C1) x 모듈로 p 의 모듈 형 역수를 계산합니다 . 즉 , 일반적으로 복호화 인자라고하는 (C1) -x 입니다.
다음 공식을 사용하여 일반 텍스트를 얻습니다-
C2 × (C1)-x mod p = Plaintext이 예에서 개인 키 x = 5를 사용하여 암호문 C = (C1, C2) = (15, 9)를 해독하려면 암호 해독 계수는 다음과 같습니다.
15-5 mod 17 = 9일반 텍스트 추출 P = (9 × 9) mod 17 = 13.
ElGamal 분석
ElGamal 시스템에서 각 사용자는 개인 키 x를 갖습니다. 그리고 가지고three components 공개 키- prime modulus p, generator g, and public Y = gx mod p. ElGamal의 강점은 이산 로그 문제의 난이도에 기반합니다.
보안 키 크기는 일반적으로> 1024 비트입니다. 오늘날에는 2048 비트 길이의 키도 사용됩니다. 처리 속도 측면에서 Elgamal은 매우 느리며 주로 키 인증 프로토콜에 사용됩니다. 더 높은 처리 효율성으로 인해 ElGamal의 Elliptic Curve 변형이 점점 인기를 얻고 있습니다.
ECC (타원 곡선 암호화)
ECC (Elliptic Curve Cryptography)는 보안이 이산 로그 문제의 특수 버전을 기반으로하는 암호화 도구 및 프로토콜 제품군을 설명하는 데 사용되는 용어입니다. p 모듈로 숫자를 사용하지 않습니다.
ECC는 타원 곡선이라고하는 수학적 개체와 관련된 숫자 집합을 기반으로합니다. 모듈로 p의 숫자와 마찬가지로이 숫자의 배수를 더하고 계산하는 규칙이 있습니다.
ECC에는 ElGamal 암호화 및 디지털 서명 알고리즘과 같은 모듈 식 숫자를 위해 처음 설계된 다양한 암호화 체계가 포함되어 있습니다.
이산 로그 문제는 타원 곡선의 점에 적용될 때 훨씬 더 어렵다고 믿어집니다. 그러면 모듈로 p에서 타원 곡선의 점으로 전환 할 수 있습니다. 또한 타원 곡선 기반 변형을 사용하면 더 짧은 키로 동등한 보안 수준을 얻을 수 있습니다.
키가 짧으면 두 가지 이점이 있습니다.
- 손쉬운 키 관리
- 효율적인 계산
이러한 이점은 타원 곡선 기반의 암호화 체계 변형을 컴퓨팅 리소스가 제한된 애플리케이션에 매우 매력적으로 만듭니다.
RSA 및 ElGamal 체계 – 비교
다양한 측면에서 RSA와 ElGamal 체계를 간단히 비교해 보겠습니다.
| RSA | ElGamal |
|---|---|
| 암호화에 더 효율적입니다. | 암호 해독에 더 효율적입니다. |
| 암호 해독에는 덜 효율적입니다. | 암호 해독에 더 효율적입니다. |
| 특정 보안 수준의 경우 RSA에 긴 키가 필요합니다. | 동일한 수준의 보안을 위해 매우 짧은 키가 필요합니다. |
| 널리 받아 들여지고 사용됩니다. | 새롭고 시장에서 그다지 인기가 없습니다. |