기계 학습-기술
기계 학습은 폭이 매우 넓고 여러 영역에 걸친 기술이 필요합니다. 머신 러닝 전문가가되기 위해 습득해야하는 기술은 다음과 같습니다.
- Statistics
- 확률 이론
- Calculus
- 최적화 기술
- Visualization
머신 러닝의 다양한 기술의 필요성
어떤 기술을 습득해야하는지에 대한 간략한 아이디어를 제공하기 위해 몇 가지 예를 살펴 보겠습니다.
수학적 표기법
대부분의 기계 학습 알고리즘은 수학을 기반으로합니다. 알아야 할 수학 수준은 아마도 초급 수준 일 것입니다. 중요한 것은 수학자가 방정식에서 사용하는 표기법을 읽을 수 있어야한다는 것입니다. 예를 들어, 표기법을 읽고 의미를 이해할 수 있다면 기계 학습을 배울 준비가 된 것입니다. 그렇지 않다면 수학 지식을 연마해야 할 수도 있습니다.
$$ f_ {AN} (net- \ theta) = \ begin {cases} \ gamma & if \ : net- \ theta \ geq \ epsilon \\ net- \ theta & if-\ epsilon <net- \ theta <\ 엡실론 \\-\ 감마 & if \ : net- \ theta \ leq- \ epsilon \ end {cases} $$
$$ \ displaystyle \\\ max \ limits _ {\ alpha} \ begin {bmatrix} \ displaystyle \ sum \ limits_ {i = 1} ^ m \ alpha- \ frac {1} {2} \ displaystyle \ sum \ limits_ { i, j = 1} ^ m label ^ \ left (\ begin {array} {c} i \\ \ end {array} \ right) \ cdot \ : label ^ \ left (\ begin {array} {c} j \\ \ end {array} \ right) \ cdot \ : a_ {i} \ cdot \ : a_ {j} \ langle x ^ \ left (\ begin {array} {c} i \\ \ end {array} \ 오른쪽), x ^ \ left (\ begin {array} {c} j \\ \ end {array} \ right) \ rangle \ end {bmatrix} $$
$$ f_ {AN} (net- \ theta) = \ left (\ frac {e ^ {\ lambda (net- \ theta)}-e ^ {-\ lambda (net- \ theta)}} {e ^ { \ lambda (net- \ theta)} + e ^ {-\ lambda (net- \ theta)}} \ right) \; $$
확률 이론
다음은 확률 이론에 대한 현재 지식을 테스트하는 예입니다. 조건부 확률로 분류.
$$ p (c_ {i} | x, y) \; = \ frac {p (x, y | c_ {i}) \; p (c_ {i}) \;} {p (x, y) \ ;} $$
이러한 정의를 통해 베이지안 분류 규칙을 정의 할 수 있습니다.
- P (c1 | x, y)> P (c2 | x, y)이면 클래스는 c1입니다.
- P (c1 | x, y) <P (c2 | x, y)이면 클래스는 c2입니다.
최적화 문제
다음은 최적화 기능입니다.
$$ \ displaystyle \\\ max \ limits _ {\ alpha} \ begin {bmatrix} \ displaystyle \ sum \ limits_ {i = 1} ^ m \ alpha- \ frac {1} {2} \ displaystyle \ sum \ limits_ { i, j = 1} ^ m label ^ \ left (\ begin {array} {c} i \\ \ end {array} \ right) \ cdot \ : label ^ \ left (\ begin {array} {c} j \\ \ end {array} \ right) \ cdot \ : a_ {i} \ cdot \ : a_ {j} \ langle x ^ \ left (\ begin {array} {c} i \\ \ end {array} \ 오른쪽), x ^ \ left (\ begin {array} {c} j \\ \ end {array} \ right) \ rangle \ end {bmatrix} $$
다음 제약 조건에 따라-
$$ \ alpha \ geq0, 및 \ : \ displaystyle \ sum \ limits_ {i-1} ^ m \ alpha_ {i} \ cdot \ : label ^ \ left (\ begin {array} {c} i \\ \ end {배열} \ 오른쪽) = 0 $$
위의 내용을 읽고 이해할 수 있다면 모든 준비가 완료된 것입니다.
심상
대부분의 경우 데이터 분포를 이해하고 알고리즘 출력 결과를 해석하려면 다양한 유형의 시각화 플롯을 이해해야합니다.
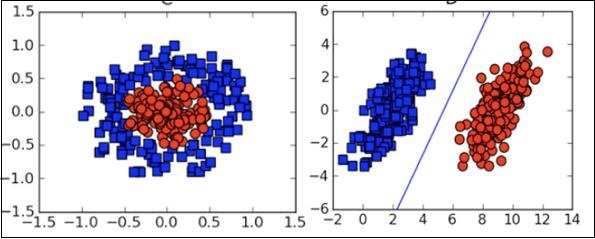
위의 기계 학습의 이론적 측면 외에도 이러한 알고리즘을 코딩하려면 좋은 프로그래밍 기술이 필요합니다.
그렇다면 ML을 구현하려면 무엇이 필요합니까? 다음 장에서 이에 대해 살펴 보겠습니다.