모델링 및 시뮬레이션-데이터베이스
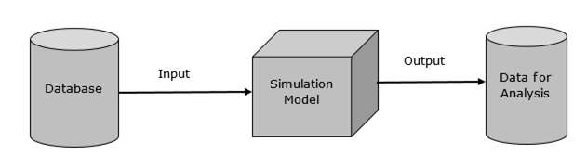
모델링 및 시뮬레이션에서 데이터베이스의 목적은 분석 및 테스트 목적으로 데이터 표현과 그 관계를 제공하는 것입니다. 첫 번째 데이터 모델은 1980 년 Edgar Codd에 의해 도입되었습니다. 다음은 모델의 두드러진 특징입니다.
데이터베이스는 정보와 그 관계를 정의하는 다양한 데이터 개체의 모음입니다.
규칙은 객체의 데이터에 대한 제약을 정의하기위한 것입니다.
정보 검색을 위해 개체에 작업을 적용 할 수 있습니다.
처음에 데이터 모델링은 엔터티가 데이터의 정보 유형이고 관계가 엔터티 간의 연결을 나타내는 엔터티 및 관계의 개념을 기반으로했습니다.
데이터 모델링의 최신 개념은 개체가 컴퓨터 프로그래밍에서 템플릿으로 사용되는 클래스로 표현되는 개체 지향 디자인입니다. 이름, 속성, 제약 조건 및 다른 클래스의 개체와의 관계를 갖는 클래스입니다.
기본 표현은 다음과 같습니다.
데이터 표현
이벤트에 대한 데이터 표현
시뮬레이션 이벤트에는 이벤트 이름 및 관련 시간 정보와 같은 속성이 있습니다. 입력 파일 매개 변수와 연관된 입력 데이터 세트를 사용하여 제공된 시뮬레이션의 실행을 나타내며 그 결과를 데이터 파일과 연관된 여러 파일에 저장된 출력 데이터 세트로 제공합니다.
입력 파일에 대한 데이터 표현
모든 시뮬레이션 프로세스에는 입력 데이터 파일에 표시되는 다른 입력 데이터 세트와 관련 매개 변수 값이 필요합니다. 입력 파일은 시뮬레이션을 처리하는 소프트웨어와 연관됩니다. 데이터 모델은 데이터 파일과의 연관으로 참조 된 파일을 나타냅니다.
출력 파일에 대한 데이터 표현
시뮬레이션 프로세스가 완료되면 다양한 출력 파일을 생성하고 각 출력 파일은 데이터 파일로 표현됩니다. 각 파일에는 이름, 설명 및 범용 요소가 있습니다. 데이터 파일은 두 개의 파일로 분류됩니다. 첫 번째 파일에는 숫자 값이 포함되고 두 번째 파일에는 숫자 파일의 내용에 대한 설명 정보가 포함됩니다.
모델링 및 시뮬레이션의 신경망
신경망은 인공 지능의 한 분야입니다. 신경망은 단위로 명명 된 많은 프로세서의 네트워크이며 각 단위는 작은 로컬 메모리를 가지고 있습니다. 각 장치는 숫자 데이터를 전달하는 연결이라는 이름의 단방향 통신 채널로 연결됩니다. 각 장치는 로컬 데이터와 연결에서 수신하는 입력에서만 작동합니다.
역사
시뮬레이션의 역사적 관점은 연대순으로 나열됩니다.
최초의 신경 모델은 1940 작성자 : McCulloch & Pitts.
에 1949, Donald Hebb는 뉴런의 개념을 지적하는 책“행동의 조직”을 썼습니다.
에 1950, 컴퓨터가 발전함에 따라 이러한 이론에 대한 모델을 만드는 것이 가능해졌습니다. IBM 연구 실험실에서 수행했습니다. 그러나 노력은 실패했고 나중에는 성공했습니다.
에 1959, Bernard Widrow 및 Marcian Hoff는 ADALINE 및 MADALINE이라는 모델을 개발했습니다. 이 모델에는 다중 ADAptive LINear 요소가 있습니다. MADALINE은 실제 문제에 적용된 최초의 신경망이었습니다.
에 1962, 퍼셉트론 모델은 Rosenblatt에 의해 개발되었으며 간단한 패턴 분류 문제를 해결할 수 있습니다.
에 1969, Minsky & Papert는 계산에서 퍼셉트론 모델의 한계에 대한 수학적 증거를 제공했습니다. 퍼셉트론 모델로는 X-OR 문제를 해결할 수 없다고합니다. 이러한 단점으로 인해 신경망이 일시적으로 감소했습니다.
에 1982, Caltech의 John Hopfield는 양방향 라인을 사용하는 기계를 만들기 위해 National Academy of Sciences에 종이에 대한 아이디어를 발표했습니다. 이전에는 단방향 선이 사용되었습니다.
상징적 방법을 포함하는 전통적인 인공 지능 기술이 실패하면 신경망을 사용해야합니다. 신경망에는 이러한 문제를 해결하는 데 필요한 컴퓨팅 성능을 제공하는 대규모 병렬 처리 기술이 있습니다.
응용 분야
신경망은 음성 합성 기계, 패턴 인식, 진단 문제 감지, 로봇 제어 보드 및 의료 장비에 사용될 수 있습니다.
모델링 및 시뮬레이션의 퍼지 세트
앞서 논의한 바와 같이 연속 시뮬레이션의 각 프로세스는 미분 방정식과 그 매개 변수 (예 : a, b, c, d> 0)에 따라 달라집니다. 일반적으로 점 추정은 모델에서 계산되고 사용됩니다. 그러나 때로는 이러한 추정치가 불확실하므로 미지의 매개 변수 추정치를 제공하는 미분 방정식에 퍼지 숫자가 필요합니다.
퍼지 세트 란 무엇입니까?
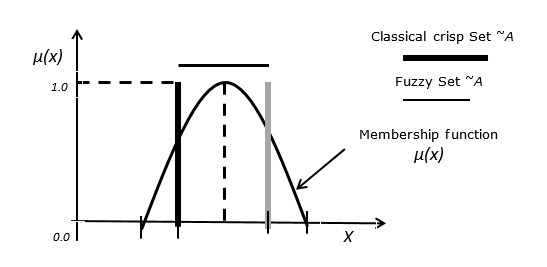
클래식 세트에서 요소는 세트의 구성원이거나 그렇지 않습니다. 퍼지 세트는 클래식 세트로 정의됩니다.X 로-
A = {(x, μA (x)) | x ∈ X}
Case 1 − 기능 μA(x) 다음과 같은 속성이 있습니다-
∀x ∈ X μA (x) ≥ 0
sup x ∈ X {μA (x)} = 1
Case 2 − 퍼지 설정 B 다음과 같이 정의되다 A = {(3, 0.3), (4, 0.7), (5, 1), (6, 0.4)}이면 표준 퍼지 표기법이 다음과 같이 작성됩니다. A = {0.3/3, 0.7/4, 1/5, 0.4/6}
회원 등급이 0 인 값은 집합의 표현식에 표시되지 않습니다.
Case 3 − 퍼지 세트와 클래식 크리스피 세트의 관계.
다음 그림은 퍼지 세트와 클래식 크리스프 세트 간의 관계를 보여줍니다.