물리학-중력
소개
우주에서 발견되는 모든 천체들은 서로를 끌어 당기 며,이 천체들 사이에서 끌어 당기는 힘을 gravitational force.

중력의 보편적 법칙
우주의 모든 물체는 질량의 곱에 정비례하고 그들 사이의 거리의 제곱에 반비례하는 힘으로 다른 모든 물체를 끌어 당기는 속성을 가지고 있습니다 (아래 주어진 이미지 참조).
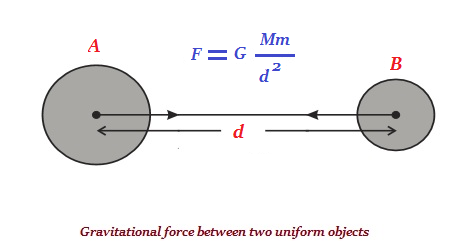
F = 두 물체 'A'와 'B'사이의 인력
M = 'A'의 질량
m = 'B'의 질량
d2 = 'A'와 'B'사이 거리의 제곱
G = 비례 상수이며 보편적 인 중력 상수로 알려져 있습니다.
G의 SI 단위는 N m2 kg–2. 힘, 거리 및 질량의 단위를 대체하여 얻습니다 (다음 방정식에 주어진 것처럼-
$$ G = \ frac {Fd ^ 2} {M \ times m} $$
Henry Cavendish는 ‘G’ 같이 6.673 × 10–11 N m2 kg–2.
Henry Cavendish는 'G'의 가치를 찾기 위해 민감한 균형을 사용했습니다.
우주 중력 법칙의 중요성
다음은 우주 중력 법칙의 현저한 의미입니다.
모든 물체 (인간 포함)를 지구에 묶는 힘을 설명합니다.
지구 주위의 달의 움직임을 설명합니다.
그것은 태양 주위의 행성들의 움직임을 설명합니다
달과 태양으로 인한 조석을 명확히
자유 낙하
물체가 지구를 향해 떨어질 때마다 가속이 필요합니다. 이 가속은 지구의 중력으로 인해 발생합니다.

지구의 중력에 의해 생성되는 가속도는 지구의 중력에 의한 가속도 (또는 중력에 의한 가속도)로 알려져 있습니다.
중력으로 인해 생성되는 가속도는 다음과 같이 표시됩니다. g.
지구의 반경이 적도 (극에서)쪽으로 증가함에 따라 ‘g’ 적도에서보다 극에서 더 커집니다.
g의 가치
g의 값은 다음과 같이 계산됩니다.
$$ g = G \ frac {M} {R ^ 2} $$
G = 보편적 인 중력 상수, 즉 = 6.7 × 10–11 N m2 kg-2
M = 지구의 질량, 즉 = 6 × 1024 kg
R = 지구 반경, 즉 = 6.4 × 106 m
So,
$$ g = \ frac {6.7 \ : \ times 10 ^ {-11} \ : Nm ^ 2 \ : kg ^ {-2} \ : \ times \ : 6 \ : \ times 10 ^ {24} \ : kg } {(6.4 \ : \ times 10 ^ 6 \ : m) ^ 2} $$
$ = 9.8 \ : m \ : s ^ {-2} $
따라서 지구의 중력에 의한 가속도 (g)는 9.8ms -2 입니다.