수직선에 유리수 그리기

정의

유리수는 분수이며 다음과 같이 수직선에 그려집니다.

Basic rules of representing rational no. on number line

유리수 (분수)가 적절하면 0과 1 사이에 있습니다.
유리수 (분수)가 부적절하면 먼저 대분수로 변환 한 다음 주어진 유리수로 변환합니다. 정수와 다음 정수 사이에 있습니다.

유리수 또는 분수를 나타 내기 위해 다음 단계를 사용합니다 (예 : 수직선 에서 $ \ frac {5} {7} $) .

Step 1 − 우리는 수직선을 그립니다.

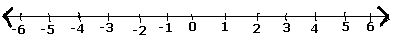
Step 2− $ \ frac {5} {7} $ 숫자는 양수이므로 0의 오른쪽에 있습니다.

Step 3− 따라서 제로 마크 뒤에는 $ \ frac {1} {7}, \ : \ frac {2} {7}, \ : \ frac {3} {7}, \ : \ frac {4} {7 }, \ : \ frac {5} {7}, \ : \ frac {6} {7}, $ 및 ( $ \ frac {7} {7} $ = 1).

Step 4− 수직선 의 유리수 $ \ frac {5} {7} $ 는 다음과 같습니다.

예 1 :

플롯 $ \ FRAC {1} {4} $ 및 $ 1 \ FRAC {2} {4} $ 아래 번호 라인

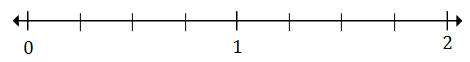
해결책

Step 1:

$ \ frac {1} {4} $ (A)는 0과 1 사이에 있습니다. $ 1 \ frac {2} {4} $ (B) 1과 2 사이에 있음

Step 2:

분수의 맨 아래가 4이므로 각 분할은 네 부분으로 나뉩니다.

$ \ frac {1} {4} $ 는 0 다음의 첫 번째 마크이므로 점 A는 $ \ frac {1} {4} $를 나타냅니다.

$ 1 \ frac {2} {4} $ 는 1 다음의 두 번째 마크이므로 점 B는 $ 1 \ frac {2} {4} $를 나타냅니다.

예 2 :

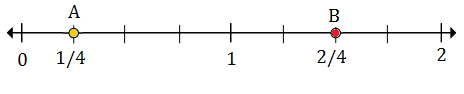
플롯 $ \ FRAC {5} {8} $ 및 $ 2 \ FRAC {3} {8} $ 아래 번호 라인

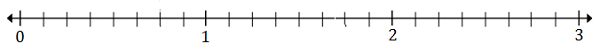
해결책

Step 1:

$ \ frac {5} {8} $ 8 (A)는 0과 1 사이에 있습니다. $ 2 \ frac {3} {8} $ (B) 2 ~ 3 개

Step 2:

분수의 하단이 8이므로 각 분할은 8 개 부분으로 나뉩니다.

$ \ frac {5} {8} $ 는 0 이후 다섯 번째 마크이므로 점 A는 $ \ frac {5} {8} $를 나타냅니다.

$ 2 \ frac {3} {8} $ 는 2 이후 세 번째 마크이므로 점 B는 $ 2 \ frac {3} {8} $를 나타냅니다.