Python-분할 및 정복

분할 및 정복 접근 방식에서는 손에 들고있는 문제가 더 작은 하위 문제로 분할 된 다음 각 문제가 독립적으로 해결됩니다. 하위 문제를 더 작은 하위 문제로 계속 나누면 결국 더 이상 분할이 불가능한 단계에 도달 할 수 있습니다. 이러한 "원자 적"가장 작은 하위 문제 (분수)가 해결됩니다. 모든 하위 문제의 해결은 원래 문제의 해결을 얻기 위해 마침내 병합됩니다.

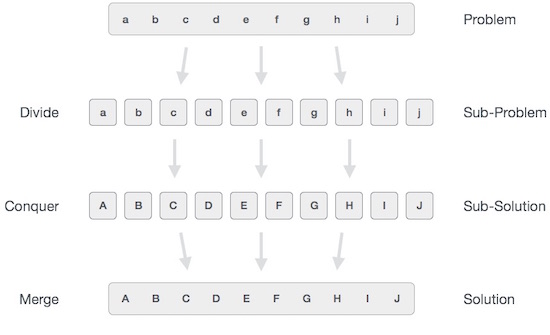
광범위하게 우리는 이해할 수 있습니다 divide-and-conquer 3 단계 프로세스로 접근합니다.

나누기 / 끊기

이 단계에는 문제를 더 작은 하위 문제로 나누는 작업이 포함됩니다. 하위 문제는 원래 문제의 일부를 나타내야합니다. 이 단계는 일반적으로 하위 문제가 더 이상 나눌 수 없을 때까지 문제를 나누기 위해 재귀 적 접근 방식을 취합니다. 이 단계에서 하위 문제는 본질적으로 원자가되지만 여전히 실제 문제의 일부를 나타냅니다.

정복 / 해결

이 단계는 해결해야 할 작은 하위 문제를 많이받습니다. 일반적으로이 수준에서 문제는 자체적으로 '해결 된'것으로 간주됩니다.

병합 / 결합

작은 하위 문제가 해결되면이 단계는 원래 문제의 솔루션을 공식화 할 때까지 반복적으로 결합합니다. 이 알고리즘 접근 방식은 재귀 적으로 작동하며 정복 및 병합 단계가 너무 가깝게 작동하여 하나로 표시됩니다.

예

다음 프로그램은 divide-and-conquer 바이너리 검색이 파이썬을 사용하여 구현되는 프로그래밍 방식.

바이너리 검색 구현

이진 검색에서 정렬 된 요소 목록을 가져와 목록 중간에있는 요소를 찾기 시작합니다. 검색 값이 목록의 중간 값과 일치하면 검색을 완료합니다. 그렇지 않으면 검색된 항목의 값에 따라 목록의 오른쪽 또는 왼쪽 절반을 처리할지 여부를 선택하여 요소 목록의 절반을 제거합니다. 목록이 정렬되어 있고 선형 검색보다 훨씬 빠르기 때문에 가능합니다. 여기서 우리는 주어진 목록을 나누고 목록의 적절한 절반을 선택하여 정복합니다. 요소를 찾거나 목록에 없다는 결론을 내릴 때까지이 approcah를 반복합니다.

def bsearch(list, val):

    list_size = len(list) - 1

    idx0 = 0
    idxn = list_size
# Find the middle most value

    while idx0 <= idxn:
        midval = (idx0 + idxn)// 2

        if list[midval] == val:
            return midval
# Compare the value the middle most value
        if val > list[midval]:
            idx0 = midval + 1
        else:
            idxn = midval - 1

    if idx0 > idxn:
        return None
# Initialize the sorted list
list = [2,7,19,34,53,72]

# Print the search result
print(bsearch(list,72))
print(bsearch(list,11))

위의 코드가 실행되면 다음과 같은 결과가 생성됩니다.

5
None