SciPy-퀵 가이드
Sigh Pi로 발음되는 SciPy는 수학, 과학 및 엔지니어링 계산을 수행하기 위해 BSD 라이센스 라이브러리 아래에 배포되는 과학 파이썬 오픈 소스입니다.
SciPy 라이브러리는 편리하고 빠른 N 차원 배열 조작을 제공하는 NumPy에 의존합니다. SciPy 라이브러리는 NumPy 배열과 함께 작동하도록 구축되었으며 수치 통합 및 최적화를위한 루틴과 같은 많은 사용자 친화적이고 효율적인 수치 사례를 제공합니다. 함께 모든 인기있는 운영 체제에서 실행되고 설치가 빠르며 무료입니다. NumPy 및 SciPy는 사용하기 쉽지만 세계 유수의 과학자 및 엔지니어가 신뢰할 수있을만큼 강력합니다.
SciPy 하위 패키지
SciPy는 다양한 과학 컴퓨팅 영역을 다루는 하위 패키지로 구성됩니다. 다음 표에 요약되어 있습니다.
| scipy.cluster | 벡터 양자화 / Kmeans |
| scipy.constants | 물리 및 수학 상수 |
| scipy.fftpack | 푸리에 변환 |
| scipy.integrate | 통합 루틴 |
| scipy.interpolate | 보간 |
| scipy.io | 데이터 입력 및 출력 |
| scipy.linalg | 선형 대수 루틴 |
| scipy.ndimage | n 차원 이미지 패키지 |
| scipy.odr | 직교 거리 회귀 |
| scipy.optimize | 최적화 |
| scipy.signal | 신호 처리 |
| scipy.sparse | 희소 행렬 |
| scipy.spatial | 공간 데이터 구조 및 알고리즘 |
| scipy.special | 특별한 수학 함수 |
| scipy.stats | 통계 |
데이터 구조
SciPy에서 사용하는 기본 데이터 구조는 NumPy 모듈에서 제공하는 다차원 배열입니다. NumPy는 선형 대수, 푸리에 변환 및 난수 생성을위한 일부 기능을 제공하지만 SciPy에서 동등한 기능의 일반성은 제공하지 않습니다.
표준 Python 배포는 SciPy 모듈과 함께 제공되지 않습니다. 가벼운 대안은 인기있는 Python 패키지 설치 프로그램을 사용하여 SciPy를 설치하는 것입니다.
pip install pandas우리가 설치하면 Anaconda Python package, Pandas는 기본적으로 설치됩니다. 다음은 다른 운영 체제에 설치하기위한 패키지 및 링크입니다.
윈도우
Anaconda (에서 https://www.continuum.io)는 SciPy 스택 용 무료 Python 배포판입니다. Linux 및 Mac에서도 사용할 수 있습니다.
Canopy (https://www.enthought.com/products/canopy/)은 무료로 제공되며 Windows, Linux 및 Mac 용 전체 SciPy 스택이 포함 된 상업용 배포 용으로도 제공됩니다.
Python (x,y)− Windows OS 용 SciPy 스택 및 Spyder IDE가 포함 된 무료 Python 배포판입니다. (에서 다운로드 가능https://python-xy.github.io/)
리눅스
각 Linux 배포판의 패키지 관리자는 SciPy 스택에 하나 이상의 패키지를 설치하는 데 사용됩니다.
우분투
다음 경로를 사용하여 Ubuntu에 Python을 설치할 수 있습니다.
sudo apt-get install python-numpy python-scipy
python-matplotlibipythonipython-notebook python-pandas python-sympy python-nose페도라
다음 경로를 사용하여 Fedora에 Python을 설치할 수 있습니다.
sudo yum install numpyscipy python-matplotlibipython python-pandas
sympy python-nose atlas-devel기본적으로 모든 NumPy 함수는 SciPy 네임 스페이스를 통해 사용할 수 있습니다. SciPy를 가져올 때 NumPy 함수를 명시 적으로 가져올 필요가 없습니다. NumPy의 주요 객체는 동종 다차원 배열입니다. 이것은 양의 정수의 튜플에 의해 인덱싱 된 동일한 유형의 요소 (일반적으로 숫자)의 테이블입니다. NumPy에서는 차원을 축이라고합니다. 개수axes 로 불린다 rank.
이제 NumPy에서 벡터와 행렬의 기본 기능을 수정하겠습니다. SciPy는 NumPy 배열 위에 구축되므로 NumPy 기본 사항에 대한 이해가 필요합니다. 선형 대수의 대부분은 행렬 만 다루기 때문에.
NumPy 벡터
벡터는 여러 가지 방법으로 만들 수 있습니다. 그들 중 일부는 아래에 설명되어 있습니다.
Python 배열과 유사한 객체를 NumPy로 변환
다음 예를 살펴 보겠습니다.
import numpy as np
list = [1,2,3,4]
arr = np.array(list)
print arr위 프로그램의 출력은 다음과 같습니다.
[1 2 3 4]내장 NumPy 배열 생성
NumPy에는 처음부터 배열을 생성하는 기능이 내장되어 있습니다. 이러한 기능 중 일부는 아래에 설명되어 있습니다.
zeros () 사용
zeros (shape) 함수는 지정된 모양으로 0 값으로 채워진 배열을 만듭니다. 기본 dtype은 float64입니다. 다음 예를 살펴 보겠습니다.
import numpy as np
print np.zeros((2, 3))위 프로그램의 출력은 다음과 같습니다.
array([[ 0., 0., 0.],
[ 0., 0., 0.]])ones () 사용
ones (shape) 함수는 1 개의 값으로 채워진 배열을 생성합니다. 다른 모든 측면에서 0과 동일합니다. 다음 예를 살펴 보겠습니다.
import numpy as np
print np.ones((2, 3))위 프로그램의 출력은 다음과 같습니다.
array([[ 1., 1., 1.],
[ 1., 1., 1.]])arange () 사용
arange () 함수는 정기적으로 증가하는 값으로 배열을 만듭니다. 다음 예를 살펴 보겠습니다.
import numpy as np
print np.arange(7)위의 프로그램은 다음과 같은 출력을 생성합니다.
array([0, 1, 2, 3, 4, 5, 6])값의 데이터 유형 정의
다음 예를 살펴 보겠습니다.
import numpy as np
arr = np.arange(2, 10, dtype = np.float)
print arr
print "Array Data Type :",arr.dtype위의 프로그램은 다음과 같은 출력을 생성합니다.
[ 2. 3. 4. 5. 6. 7. 8. 9.]
Array Data Type : float64linspace () 사용
linspace () 함수는 지정된 수의 요소로 배열을 생성하며, 지정된 시작 값과 끝 값 사이에 동일한 간격을 둡니다. 다음 예를 살펴 보겠습니다.
import numpy as np
print np.linspace(1., 4., 6)위의 프로그램은 다음과 같은 출력을 생성합니다.
array([ 1. , 1.6, 2.2, 2.8, 3.4, 4. ])매트릭스
행렬은 연산을 통해 2 차원 특성을 유지하는 특수한 2 차원 배열입니다. * (행렬 곱셈) 및 ** (행렬 전력)과 같은 특정 특수 연산자가 있습니다. 다음 예를 살펴 보겠습니다.
import numpy as np
print np.matrix('1 2; 3 4')위의 프로그램은 다음과 같은 출력을 생성합니다.
matrix([[1, 2],
[3, 4]])행렬의 켤레 전치
이 기능은 (복잡한) 켤레 전치 값을 반환합니다. self. 다음 예를 살펴 보겠습니다.
import numpy as np
mat = np.matrix('1 2; 3 4')
print mat.H위의 프로그램은 다음과 같은 출력을 생성합니다.
matrix([[1, 3],
[2, 4]])행렬 전치
이 기능은 self의 전치를 반환합니다. 다음 예를 살펴 보겠습니다.
import numpy as np
mat = np.matrix('1 2; 3 4')
mat.T위의 프로그램은 다음과 같은 출력을 생성합니다.
matrix([[1, 3],
[2, 4]])행렬을 전치 할 때 행이 원본의 열인 새 행렬을 만듭니다. 반면에 켤레 전치 (conjugate transposition)는 각 행렬 요소의 행과 열 인덱스를 교환합니다. 역행렬은 원래 행렬과 곱하면 단위 행렬이되는 행렬입니다.
K-means clustering레이블이 지정되지 않은 데이터 집합에서 군집과 군집 중심을 찾는 방법입니다. 직관적으로 우리는 클러스터를 데이터 포인트 그룹으로 구성한다고 생각할 수 있습니다. 데이터 포인트 그룹은 클러스터 외부 포인트까지의 거리에 비해 포인트 간 거리가 작습니다. K 중심의 초기 집합이 주어지면 K- 평균 알고리즘은 다음 두 단계를 반복합니다.
각 센터에 대해 다른 센터보다 더 가까운 훈련 포인트 (군집)의 하위 집합이 식별됩니다.
각 군집의 데이터 포인트에 대한 각 특징의 평균이 계산되고이 평균 벡터가 해당 군집의 새로운 중심이됩니다.
이 두 단계는 센터가 더 이상 움직이지 않거나 할당이 더 이상 변경되지 않을 때까지 반복됩니다. 그런 다음 새로운 포인트x가장 가까운 프로토 타입의 클러스터에 할당 할 수 있습니다. SciPy 라이브러리는 클러스터 패키지를 통해 K-Means 알고리즘의 좋은 구현을 제공합니다. 사용 방법을 이해합시다.
SciPy에서 K-Means 구현
SciPy에서 K-Means를 구현하는 방법을 이해할 것입니다.
K- 평균 가져 오기
가져온 각 함수의 구현 및 사용법을 살펴 보겠습니다.
from SciPy.cluster.vq import kmeans,vq,whiten데이터 생성
클러스터링을 탐색하기 위해 일부 데이터를 시뮬레이션해야합니다.
from numpy import vstack,array
from numpy.random import rand
# data generation with three features
data = vstack((rand(100,3) + array([.5,.5,.5]),rand(100,3)))이제 데이터를 확인해야합니다. 위의 프로그램은 다음과 같은 출력을 생성합니다.
array([[ 1.48598868e+00, 8.17445796e-01, 1.00834051e+00],
[ 8.45299768e-01, 1.35450732e+00, 8.66323621e-01],
[ 1.27725864e+00, 1.00622682e+00, 8.43735610e-01],
…………….기능별로 관찰 그룹을 정규화합니다. K-Means를 실행하기 전에 미백으로 관찰 세트의 각 특징 차원을 다시 조정하는 것이 좋습니다. 각 기능은 모든 관측치에 대한 표준 편차로 나누어 단위 분산을 제공합니다.
데이터를 희게
데이터를 희게하기 위해 다음 코드를 사용해야합니다.
# whitening of data
data = whiten(data)3 개의 군집으로 K- 평균 계산하기
이제 다음 코드를 사용하여 세 개의 클러스터로 K- 평균을 계산해 보겠습니다.
# computing K-Means with K = 3 (2 clusters)
centroids,_ = kmeans(data,3)위의 코드는 K 클러스터를 형성하는 관측 벡터 세트에 대해 K- 평균을 수행합니다. K-Means 알고리즘은 마지막 반복이 일부 임계 값보다 작기 때문에 충분한 진행, 즉 왜곡의 변화가 이루어질 수 없을 때까지 중심을 조정합니다. 여기에서 아래 주어진 코드를 사용하여 centroids 변수를 인쇄하여 클러스터의 중심을 관찰 할 수 있습니다.
print(centroids)위의 코드는 다음 출력을 생성합니다.
print(centroids)[ [ 2.26034702 1.43924335 1.3697022 ]
[ 2.63788572 2.81446462 2.85163854]
[ 0.73507256 1.30801855 1.44477558] ]아래에 제공된 코드를 사용하여 각 값을 클러스터에 할당합니다.
# assign each sample to a cluster
clx,_ = vq(data,centroids)그만큼 vq 함수는 'M'의 각 관측 벡터를 'N'과 비교합니다. obs중심으로 배열하고 가장 가까운 군집에 관측치를 할당합니다. 각 관측치의 군집과 왜곡을 반환합니다. 왜곡도 확인할 수 있습니다. 다음 코드를 사용하여 각 관측 값의 군집을 확인하겠습니다.
# check clusters of observation
print clx위의 코드는 다음 출력을 생성합니다.
array([1, 1, 0, 1, 1, 1, 0, 1, 0, 0, 1, 1, 1, 0, 0, 1, 1, 0, 0, 1, 0, 2, 0, 2, 0, 1, 1, 1,
0, 0, 1, 1, 0, 0, 1, 1, 0, 0, 0, 0, 1, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 0, 0, 0, 1, 1, 0, 0,
0, 1, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0,
0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 2, 1, 2, 2, 2, 2, 2, 2, 2, 2, 0, 2, 0, 2, 2, 2, 2, 2, 0, 0,
2, 2, 2, 1, 0, 2, 0, 2, 2, 2, 2, 2, 2, 2, 2, 2, 0, 2, 2, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 0, 2, 0, 2, 2, 2, 2, 2, 2, 2, 2, 2, 0, 2, 2, 2, 2, 0, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2], dtype=int32)위 배열의 고유 한 값 0, 1, 2는 클러스터를 나타냅니다.
SciPy 상수 패키지는 일반 과학 분야에서 사용되는 광범위한 상수를 제공합니다.
SciPy 상수 패키지
그만큼 scipy.constants package다양한 상수를 제공합니다. 필요한 상수를 가져 와서 요구 사항에 따라 사용해야합니다. 이러한 상수 변수를 가져오고 사용하는 방법을 살펴 보겠습니다.
먼저 다음 예제를 고려하여 'pi'값을 비교해 보겠습니다.
#Import pi constant from both the packages
from scipy.constants import pi
from math import pi
print("sciPy - pi = %.16f"%scipy.constants.pi)
print("math - pi = %.16f"%math.pi)위의 프로그램은 다음과 같은 출력을 생성합니다.
sciPy - pi = 3.1415926535897931
math - pi = 3.1415926535897931사용 가능한 상수 목록
다음 표는 다양한 상수를 간략하게 설명합니다.
수학 상수
| Sr. No. | 일정한 | 기술 |
|---|---|---|
| 1 | 파이 | 파이 |
| 2 | 황금빛 | 황금 비율 |
물리적 상수
다음 표는 가장 일반적으로 사용되는 물리 상수를 나열합니다.
| Sr. No. | 상수 및 설명 |
|---|---|
| 1 | c 진공 상태에서 빛의 속도 |
| 2 | speed_of_light 진공 상태에서 빛의 속도 |
| 삼 | h 플랑크 상수 |
| 4 | Planck 플랑크 상수 h |
| 5 | G 뉴턴의 중력 상수 |
| 6 | e 초등학교 요금 |
| 7 | R 몰 가스 상수 |
| 8 | Avogadro Avogadro 상수 |
| 9 | k 볼츠만 상수 |
| 10 | electron_mass(OR) m_e 전자 질량 |
| 11 | proton_mass (OR) m_p 양성자 질량 |
| 12 | neutron_mass(OR)m_n 중성자 질량 |
단위
다음 표에는 SI 단위 목록이 있습니다.
| Sr. No. | 단위 | 값 |
|---|---|---|
| 1 | 밀리 | 0.001 |
| 2 | 마이크로 | 1e-06 |
| 삼 | 킬로 | 1000 |
이 단위는 yotta, zetta, exa, peta, tera …… kilo, hector,… nano, pico,…에서 zepto까지 다양합니다.
기타 중요한 상수
다음 표에는 SciPy에서 사용되는 다른 중요한 상수가 나열되어 있습니다.
| Sr. No. | 단위 | 값 |
|---|---|---|
| 1 | 그램 | 0.001kg |
| 2 | 원자 질량 | 원자 질량 상수 |
| 삼 | 정도 | 라디안 단위 |
| 4 | 분 | 1 분 (초) |
| 5 | 일 | 하루 초 |
| 6 | 인치 | 1 인치 (미터) |
| 7 | 미크론 | 1 미크론 (미터) |
| 8 | 광년 | 미터 단위로 1 광년 |
| 9 | ATM | 파스칼의 표준 대기 |
| 10 | 에이커 | 평방 미터에 1 에이커 |
| 11 | 리터 | 1 리터 (입방 미터) |
| 12 | 갤런 | 입방 미터의 1 갤런 |
| 13 | kmh | 시간당 킬로미터 (초당 미터) |
| 14 | degree_Fahrenheit | 1 화씨 (켈빈) |
| 15 | eV | 줄 단위의 1 전자 볼트 |
| 16 | hp | 1 마력 (와트) |
| 17 | 딘 | 뉴턴의 한 다인 |
| 18 | lambda2nu | 파장을 광학 주파수로 변환 |
이 모든 것을 기억하는 것은 약간 어렵습니다. 어떤 키가 어떤 기능에 해당하는지 쉽게 알 수있는 방법은scipy.constants.find()방법. 다음 예를 살펴 보겠습니다.
import scipy.constants
res = scipy.constants.physical_constants["alpha particle mass"]
print res위의 프로그램은 다음과 같은 출력을 생성합니다.
[
'alpha particle mass',
'alpha particle mass energy equivalent',
'alpha particle mass energy equivalent in MeV',
'alpha particle mass in u',
'electron to alpha particle mass ratio'
]이 메서드는 키 목록을 반환하고 키워드가 일치하지 않으면 아무것도 반환하지 않습니다.
Fourier Transformation주파수 영역에서의 동작을 확인하기 위해 시간 영역 신호에서 계산됩니다. 푸리에 변환은 신호 및 노이즈 처리, 이미지 처리, 오디오 신호 처리 등과 같은 분야에서 적용됩니다. SciPy는 사용자가 빠른 푸리에 변환을 계산할 수있는 fftpack 모듈을 제공합니다.
다음은 fftpack 모듈을 사용하여 푸리에 변환을 계산하는 데 사용되는 사인 함수의 예입니다.
고속 푸리에 변환
빠른 푸리에 변환이 무엇인지 자세히 이해합시다.
1 차원 이산 푸리에 변환
길이 N 시퀀스 x [n]의 길이 N의 FFT y [k]는 fft ()에 의해 계산되고 역변환은 ifft ()를 사용하여 계산됩니다. 다음 예를 살펴 보겠습니다.
#Importing the fft and inverse fft functions from fftpackage
from scipy.fftpack import fft
#create an array with random n numbers
x = np.array([1.0, 2.0, 1.0, -1.0, 1.5])
#Applying the fft function
y = fft(x)
print y위의 프로그램은 다음과 같은 출력을 생성합니다.
[ 4.50000000+0.j 2.08155948-1.65109876j -1.83155948+1.60822041j
-1.83155948-1.60822041j 2.08155948+1.65109876j ]다른 예를 살펴 보겠습니다.
#FFT is already in the workspace, using the same workspace to for inverse transform
yinv = ifft(y)
print yinv위의 프로그램은 다음과 같은 출력을 생성합니다.
[ 1.0+0.j 2.0+0.j 1.0+0.j -1.0+0.j 1.5+0.j ]그만큼 scipy.fftpack모듈을 사용하면 빠른 푸리에 변환을 계산할 수 있습니다. 예를 들어, (노이즈가있는) 입력 신호는 다음과 같이 보일 수 있습니다.
import numpy as np
time_step = 0.02
period = 5.
time_vec = np.arange(0, 20, time_step)
sig = np.sin(2 * np.pi / period * time_vec) + 0.5 *np.random.randn(time_vec.size)
print sig.size0.02 초의 시간 단계로 신호를 생성합니다. 마지막 명령문은 신호 sig의 크기를 인쇄합니다. 출력은 다음과 같습니다.
1000우리는 신호 주파수를 모릅니다. 신호 시그널의 샘플링 시간 단계 만 알고 있습니다. 신호는 실제 함수에서 오는 것으로 가정하므로 푸리에 변환은 대칭이됩니다. 그만큼scipy.fftpack.fftfreq() 함수는 샘플링 주파수를 생성하고 scipy.fftpack.fft() 빠른 푸리에 변환을 계산합니다.
예제의 도움으로 이것을 이해합시다.
from scipy import fftpack
sample_freq = fftpack.fftfreq(sig.size, d = time_step)
sig_fft = fftpack.fft(sig)
print sig_fft위의 프로그램은 다음과 같은 출력을 생성합니다.
array([
25.45122234 +0.00000000e+00j, 6.29800973 +2.20269471e+00j,
11.52137858 -2.00515732e+01j, 1.08111300 +1.35488579e+01j,
…….])이산 코사인 변환
ㅏ Discrete Cosine Transform (DCT)서로 다른 주파수에서 진동하는 코사인 함수의 합으로 한정된 데이터 포인트 시퀀스를 표현합니다. SciPy는 DCT에 기능을 제공합니다.dct 및 기능이있는 해당 IDCT idct. 다음 예를 살펴 보겠습니다.
from scipy.fftpack import dct
print dct(np.array([4., 3., 5., 10., 5., 3.]))위의 프로그램은 다음과 같은 출력을 생성합니다.
array([ 60., -3.48476592, -13.85640646, 11.3137085, 6., -6.31319305])역 이산 코사인 변환은 이산 코사인 변환 (DCT) 계수에서 시퀀스를 재구성합니다. idct 함수는 dct 함수의 역입니다. 다음 예를 통해이를 이해해 보겠습니다.
from scipy.fftpack import dct
print idct(np.array([4., 3., 5., 10., 5., 3.]))위의 프로그램은 다음과 같은 출력을 생성합니다.
array([ 39.15085889, -20.14213562, -6.45392043, 7.13341236,
8.14213562, -3.83035081])함수를 분석적으로 통합 할 수 없거나 분석적으로 통합하기가 매우 어려운 경우 일반적으로 수치 통합 방법으로 전환합니다. SciPy에는 수치 적분을 수행하기위한 여러 루틴이 있습니다. 그들 대부분은 같은 곳에서 발견됩니다scipy.integrate도서관. 다음 표에는 일반적으로 사용되는 몇 가지 기능이 나열되어 있습니다.
| Sr 번호 | 기능 및 설명 |
|---|---|
| 1 | quad 단일 통합 |
| 2 | dblquad 이중 통합 |
| 삼 | tplquad 트리플 통합 |
| 4 | nquad n- 다중 통합 |
| 5 | fixed_quad 가우스 구적법, 차수 n |
| 6 | quadrature 공차에 대한 가우스 구적법 |
| 7 | romberg Romberg 통합 |
| 8 | trapz 사다리꼴 규칙 |
| 9 | cumtrapz 적분을 누적 계산하기위한 사다리꼴 규칙 |
| 10 | simps 심슨의 규칙 |
| 11 | romb Romberg 통합 |
| 12 | polyint 분석 다항식 통합 (NumPy) |
| 13 | poly1d 폴리 인트 (NumPy)를위한 도우미 기능 |
단일 적분
Quad 기능은 SciPy 통합 기능의 핵심입니다. 수치 적 통합은 때때로 호출됩니다.quadrature, 따라서 이름. 일반적으로 a에서 b까지 주어진 고정 범위 에 대해 함수 f (x) 의 단일 적분을 수행하기위한 기본 선택입니다 .
$$\int_{a}^{b} f(x)dx$$
쿼드의 일반적인 형태는 다음과 같습니다. scipy.integrate.quad(f, a, b), 여기서 'f'는 통합 할 함수의 이름입니다. 반면 'a'와 'b'는 각각 하한과 상한입니다. 0과 1의 범위에 통합 된 가우스 함수의 예를 살펴 보겠습니다.
먼저 함수를 정의해야합니다 → $f(x) = e^{-x^2}$ ,이 작업은 람다 식을 사용하여 수행 한 다음 해당 함수에서 quad 메서드를 호출 할 수 있습니다.
import scipy.integrate
from numpy import exp
f= lambda x:exp(-x**2)
i = scipy.integrate.quad(f, 0, 1)
print i위의 프로그램은 다음과 같은 출력을 생성합니다.
(0.7468241328124271, 8.291413475940725e-15)quad 함수는 두 값을 반환하는데, 첫 번째 숫자는 적분 값이고 두 번째 값은 적분 값의 절대 오차 추정치입니다.
Note− quad는 첫 번째 인자로 함수를 필요로하기 때문에 exp를 인자로 직접 전달할 수 없습니다. Quad 함수는 양수 및 음수 무한대를 제한으로 허용합니다. Quad 함수는 exp, sin 및 cos와 같은 단일 변수의 표준 사전 정의 NumPy 함수를 통합 할 수 있습니다.
다중 적분
이중 및 삼중 통합의 메커니즘이 함수로 요약되었습니다. dblquad, tplquad 과 nquad. 이러한 함수는 각각 4 개 또는 6 개의 인수를 통합합니다. 모든 내부 적분의 한계는 함수로 정의되어야합니다.
이중 적분
일반적인 형태 dblquadscipy.integrate.dblquad (func, a, b, gfun, hfun)입니다. 여기서 func는 통합 할 함수의 이름이고, 'a'와 'b'는 각각 x 변수의 하한 및 상한이며, gfun 및 hfun은 하한과 상한을 정의하는 함수의 이름입니다. y 변수의.
예를 들어 이중 적분 방법을 수행해 보겠습니다.
$$\int_{0}^{1/2} dy \int_{0}^{\sqrt{1-4y^2}} 16xy \:dx$$
람다 식을 사용하여 함수 f, g, h를 정의합니다. g와 h가 상수 인 경우에도 많은 경우에있을 수 있으므로 여기서 하한에 대해 수행 한 것처럼 함수로 정의해야합니다.
import scipy.integrate
from numpy import exp
from math import sqrt
f = lambda x, y : 16*x*y
g = lambda x : 0
h = lambda y : sqrt(1-4*y**2)
i = scipy.integrate.dblquad(f, 0, 0.5, g, h)
print i위의 프로그램은 다음과 같은 출력을 생성합니다.
(0.5, 1.7092350012594845e-14)위에서 설명한 루틴 외에도 scipy.integrate에는 n- 폴드 다중 통합을 수행하는 nquad와 다양한 통합 알고리즘을 구현하는 기타 루틴을 비롯한 여러 통합 루틴이 있습니다. 그러나 quad 및 dblquad는 수치 적분에 대한 대부분의 요구 사항을 충족합니다.
이 장에서는 SciPy에서 보간이 어떻게 도움이되는지 설명합니다.
보간이란 무엇입니까?
보간은 선이나 곡선에서 두 점 사이의 값을 찾는 과정입니다. 의미를 기억할 수 있도록 '인터'라는 단어의 첫 부분을 '입력'을 의미하는 것으로 생각해야합니다. 이는 원래 가지고 있던 데이터 '내부'를 보도록 상기시켜줍니다. 이 도구 인 보간은 통계에서 유용 할뿐만 아니라 과학, 비즈니스 또는 기존의 두 데이터 포인트에 속하는 값을 예측해야하는 경우에도 유용합니다.
데이터를 생성하고이 보간이 scipy.interpolate 꾸러미.
import numpy as np
from scipy import interpolate
import matplotlib.pyplot as plt
x = np.linspace(0, 4, 12)
y = np.cos(x**2/3+4)
print x,y위의 프로그램은 다음과 같은 출력을 생성합니다.
(
array([0., 0.36363636, 0.72727273, 1.09090909, 1.45454545, 1.81818182,
2.18181818, 2.54545455, 2.90909091, 3.27272727, 3.63636364, 4.]),
array([-0.65364362, -0.61966189, -0.51077021, -0.31047698, -0.00715476,
0.37976236, 0.76715099, 0.99239518, 0.85886263, 0.27994201,
-0.52586509, -0.99582185])
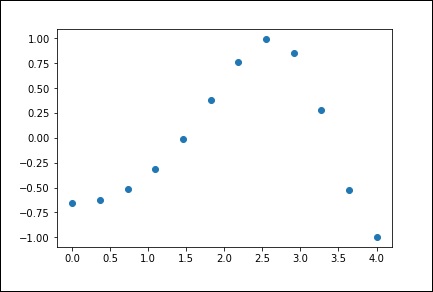
)이제 두 개의 배열이 있습니다. 이 두 배열을 공간에있는 점의 2 차원으로 가정하고 다음 프로그램을 사용하여 플로팅하고 어떻게 보이는지 살펴 보겠습니다.
plt.plot(x, y,’o’)
plt.show()위의 프로그램은 다음과 같은 출력을 생성합니다.
1 차원 보간
scipy.interpolate의 interp1d 클래스는 고정 데이터 포인트를 기반으로 함수를 생성하는 편리한 방법으로, 선형 보간을 사용하여 주어진 데이터에 의해 정의 된 도메인 내 어디에서나 평가할 수 있습니다.
위의 데이터를 사용하여 보간 함수를 만들고 새로운 보간 그래프를 그립니다.
f1 = interp1d(x, y,kind = 'linear')
f2 = interp1d(x, y, kind = 'cubic')interp1d 함수를 사용하여 두 개의 함수 f1과 f2를 만들었습니다. 이 함수는 주어진 입력 x에 대해 y를 반환합니다. 세 번째 변수 종류는 보간 기법의 유형을 나타냅니다. 'Linear', 'Nearest', 'Zero', 'Slinear', 'Quadratic', 'Cubic'은 몇 가지 보간 기법입니다.
이제 보간의 명확한 차이를 확인하기 위해 더 많은 길이의 새 입력을 생성 해 보겠습니다. 새 데이터에 이전 데이터와 동일한 기능을 사용합니다.
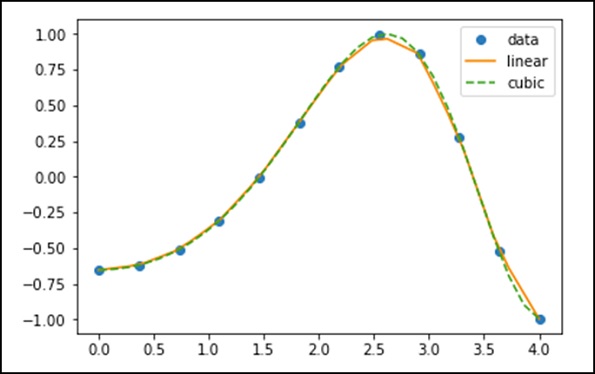
xnew = np.linspace(0, 4,30)
plt.plot(x, y, 'o', xnew, f(xnew), '-', xnew, f2(xnew), '--')
plt.legend(['data', 'linear', 'cubic','nearest'], loc = 'best')
plt.show()위의 프로그램은 다음과 같은 출력을 생성합니다.
스플라인
데이터 포인트를 통해 부드러운 곡선을 그리기 위해 제도자는 한때 기계 스플라인이라고하는 얇고 유연한 목재 스트립, 단단한 고무, 금속 또는 플라스틱을 사용했습니다. 기계식 스플라인을 사용하기 위해 디자인의 곡선을 따라 점을 신중하게 선택하여 핀을 배치 한 다음 스플라인을 구부려 각 핀에 닿았습니다.
분명히이 구성을 사용하면 스플라인이이 핀에서 곡선을 보간합니다. 다른 도면의 곡선을 재현하는 데 사용할 수 있습니다. 핀이있는 지점을 매듭이라고합니다. 매듭의 위치를 조정하여 스플라인으로 정의 된 곡선의 모양을 변경할 수 있습니다.
일 변량 스플라인
1 차원 스무딩 스플라인은 주어진 데이터 포인트 세트에 맞습니다. scipy.interpolate의 UnivariateSpline 클래스는 고정 데이터 포인트 클래스를 기반으로 함수를 생성하는 편리한 방법입니다. – scipy.interpolate.UnivariateSpline (x, y, w = None, bbox = [None, None], k = 3, s = 없음, ext = 0, check_finite = False).
Parameters − 다음은 일 변량 스플라인의 매개 변수입니다.
이것은 제공된 x, y 데이터에 k 차의 스플라인 y = spl (x)를 맞 춥니 다.
'w'-스플라인 피팅에 대한 가중치를 지정합니다. 긍정적이어야합니다. 없는 경우 (기본값) 가중치는 모두 같습니다.
's'-스무딩 조건을 지정하여 매듭 수를 지정합니다.
'k'-스무딩 스플라인의 정도. <= 5 여야합니다. 기본값은 3 차 스플라인 인 k = 3입니다.
Ext-매듭 시퀀스에 의해 정의 된 간격에없는 요소에 대한 외삽 모드를 제어합니다.
ext = 0 또는 'extrapolate'이면 외삽 된 값을 반환합니다.
ext = 1 또는 'zero'이면 0을 반환합니다.
ext = 2 또는 'raise'이면 ValueError 발생
ext = 3 of 'const'이면 경계 값을 반환합니다.
check_finite – 입력 배열에 유한 숫자 만 포함되어 있는지 확인할지 여부.
다음 예를 살펴 보겠습니다.
import matplotlib.pyplot as plt
from scipy.interpolate import UnivariateSpline
x = np.linspace(-3, 3, 50)
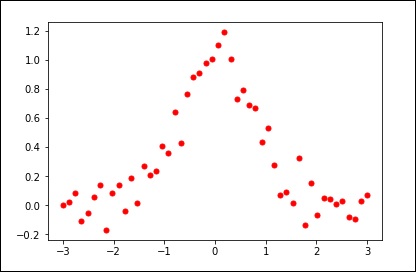
y = np.exp(-x**2) + 0.1 * np.random.randn(50)
plt.plot(x, y, 'ro', ms = 5)
plt.show()평활화 매개 변수에 기본값을 사용합니다.
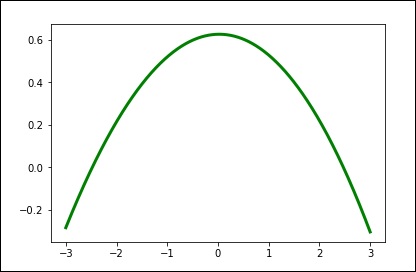
spl = UnivariateSpline(x, y)
xs = np.linspace(-3, 3, 1000)
plt.plot(xs, spl(xs), 'g', lw = 3)
plt.show()스무딩 정도를 수동으로 변경합니다.
spl.set_smoothing_factor(0.5)
plt.plot(xs, spl(xs), 'b', lw = 3)
plt.show()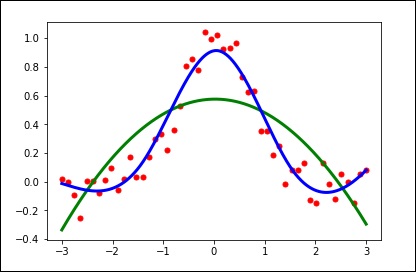
Scipy.io (입력 및 출력) 패키지는 다양한 형식의 파일을 처리 할 수있는 다양한 기능을 제공합니다. 이러한 형식 중 일부는-
- Matlab
- IDL
- 매트릭스 시장
- Wave
- Arff
- Netcdf 등
가장 일반적으로 사용되는 파일 형식에 대해 자세히 논의하겠습니다.
MATLAB
다음은 .mat 파일을로드하고 저장하는 데 사용되는 기능입니다.
| Sr. No. | 기능 및 설명 |
|---|---|
| 1 | loadmat MATLAB 파일을로드합니다. |
| 2 | savemat MATLAB 파일을 저장합니다. |
| 삼 | whosmat MATLAB 파일 내의 변수를 나열합니다. |
다음 예를 살펴 보겠습니다.
import scipy.io as sio
import numpy as np
#Save a mat file
vect = np.arange(10)
sio.savemat('array.mat', {'vect':vect})
#Now Load the File
mat_file_content = sio.loadmat(‘array.mat’)
Print mat_file_content위의 프로그램은 다음과 같은 출력을 생성합니다.
{
'vect': array([[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]]), '__version__': '1.0',
'__header__': 'MATLAB 5.0 MAT-file Platform: posix, Created on: Sat Sep 30
09:49:32 2017', '__globals__': []
}Meta 정보와 함께 배열을 볼 수 있습니다. 데이터를 메모리로 읽지 않고 MATLAB 파일의 내용을 검사하려면whosmat command 아래 그림과 같이.
import scipy.io as sio
mat_file_content = sio.whosmat(‘array.mat’)
print mat_file_content위의 프로그램은 다음과 같은 출력을 생성합니다.
[('vect', (1, 10), 'int64')]SciPy는 최적화 된 ATLAS LAPACK 과 BLAS도서관. 매우 빠른 선형 대수 기능이 있습니다. 이러한 모든 선형 대수 루틴은 2 차원 배열로 변환 될 수있는 객체를 기대합니다. 이러한 루틴의 출력도 2 차원 배열입니다.
SciPy.linalg 대 NumPy.linalg
scipy.linalg에는 numpy.linalg에있는 모든 함수가 포함됩니다. 또한 scipy.linalg에는 numpy.linalg에없는 다른 고급 기능도 있습니다. numpy.linalg에 비해 scipy.linalg를 사용하는 또 다른 장점은 항상 BLAS / LAPACK 지원으로 컴파일되는 반면 NumPy의 경우 선택 사항입니다. 따라서 NumPy가 설치된 방식에 따라 SciPy 버전이 더 빠를 수 있습니다.
선형 방정식
그만큼 scipy.linalg.solve feature는 알려지지 않은 x, y 값에 대해 선형 방정식 a * x + b * y = Z를 풉니 다.
예를 들어 다음 연립 방정식을 풀고 자한다고 가정합니다.
x + 3y + 5z = 10
2x + 5y + z = 8
2x + 3y + 8z = 3
x, y, z 값에 대한 위의 방정식을 풀기 위해 아래와 같이 역행렬을 사용하여 해 벡터를 찾을 수 있습니다.
$$\begin{bmatrix} x\\ y\\ z \end{bmatrix} = \begin{bmatrix} 1 & 3 & 5\\ 2 & 5 & 1\\ 2 & 3 & 8 \end{bmatrix}^{-1} \begin{bmatrix} 10\\ 8\\ 3 \end{bmatrix} = \frac{1}{25} \begin{bmatrix} -232\\ 129\\ 19 \end{bmatrix} = \begin{bmatrix} -9.28\\ 5.16\\ 0.76 \end{bmatrix}.$$
그러나 linalg.solve 더 빠르고 수치 적으로 안정적 일 수 있습니다.
solve 함수는 두 개의 입력 'a'와 'b'를 취하며, 여기서 'a'는 계수를 나타내고 'b'는 각각의 우변 값을 나타내고 해 배열을 반환합니다.
다음 예를 살펴 보겠습니다.
#importing the scipy and numpy packages
from scipy import linalg
import numpy as np
#Declaring the numpy arrays
a = np.array([[3, 2, 0], [1, -1, 0], [0, 5, 1]])
b = np.array([2, 4, -1])
#Passing the values to the solve function
x = linalg.solve(a, b)
#printing the result array
print x위의 프로그램은 다음과 같은 출력을 생성합니다.
array([ 2., -2., 9.])결정 인자 찾기
정사각형 행렬 A의 행렬식은 종종 | A |로 표시됩니다. 선형 대수에서 자주 사용되는 양입니다. SciPy에서 이것은det()함수. 행렬을 입력으로 사용하고 스칼라 값을 반환합니다.
다음 예를 살펴 보겠습니다.
#importing the scipy and numpy packages
from scipy import linalg
import numpy as np
#Declaring the numpy array
A = np.array([[1,2],[3,4]])
#Passing the values to the det function
x = linalg.det(A)
#printing the result
print x위의 프로그램은 다음과 같은 출력을 생성합니다.
-2.0고유 값과 고유 벡터
고유 값-고유 벡터 문제는 가장 일반적으로 사용되는 선형 대수 연산 중 하나입니다. 다음 관계를 고려하여 정사각형 행렬 (A)의 고유 값 (λ)과 해당 고유 벡터 (v)를 찾을 수 있습니다.
Av = λv
scipy.linalg.eig일반 또는 일반 고유 값 문제에서 고유 값을 계산합니다. 이 함수는 고유 값과 고유 벡터를 반환합니다.
다음 예를 살펴 보겠습니다.
#importing the scipy and numpy packages
from scipy import linalg
import numpy as np
#Declaring the numpy array
A = np.array([[1,2],[3,4]])
#Passing the values to the eig function
l, v = linalg.eig(A)
#printing the result for eigen values
print l
#printing the result for eigen vectors
print v위의 프로그램은 다음과 같은 출력을 생성합니다.
array([-0.37228132+0.j, 5.37228132+0.j]) #--Eigen Values
array([[-0.82456484, -0.41597356], #--Eigen Vectors
[ 0.56576746, -0.90937671]])특이 값 분해
SVD (특이 값 분해)는 고유 값 문제를 정사각형이 아닌 행렬로 확장 한 것으로 생각할 수 있습니다.
그만큼 scipy.linalg.svd 행렬 'a'를 두 개의 단일 행렬 'U'및 'Vh'와 a == U * S * Vh가되도록 특이 값 (실수, 음이 아님)의 1 차원 배열 's'로 분해합니다. 여기서 'S '는 주 대각선's '가있는 적절한 모양의 0 행렬입니다.
다음 예를 살펴 보겠습니다.
#importing the scipy and numpy packages
from scipy import linalg
import numpy as np
#Declaring the numpy array
a = np.random.randn(3, 2) + 1.j*np.random.randn(3, 2)
#Passing the values to the eig function
U, s, Vh = linalg.svd(a)
# printing the result
print U, Vh, s위의 프로그램은 다음과 같은 출력을 생성합니다.
(
array([
[ 0.54828424-0.23329795j, -0.38465728+0.01566714j,
-0.18764355+0.67936712j],
[-0.27123194-0.5327436j , -0.57080163-0.00266155j,
-0.39868941-0.39729416j],
[ 0.34443818+0.4110186j , -0.47972716+0.54390586j,
0.25028608-0.35186815j]
]),
array([ 3.25745379, 1.16150607]),
array([
[-0.35312444+0.j , 0.32400401+0.87768134j],
[-0.93557636+0.j , -0.12229224-0.33127251j]
])
)SciPy ndimage 서브 모듈은 이미지 처리 전용입니다. 여기서 ndimage는 n 차원 이미지를 의미합니다.
이미지 처리에서 가장 일반적인 작업 중 일부는 다음과 같습니다. & miuns;
- 입력 / 출력, 이미지 표시
- 기본 조작-자르기, 뒤집기, 회전 등
- 이미지 필터링-노이즈 제거, 선명 화 등
- 이미지 분할-다른 객체에 해당하는 레이블링 픽셀
- Classification
- 특징 추출
- Registration
SciPy를 사용하여 이들 중 일부를 달성 할 수있는 방법에 대해 논의하겠습니다.
이미지 파일 열기 및 쓰기
그만큼 misc packageSciPy에는 일부 이미지가 함께 제공됩니다. 이러한 이미지를 사용하여 이미지 조작을 학습합니다. 다음 예를 살펴 보겠습니다.
from scipy import misc
f = misc.face()
misc.imsave('face.png', f) # uses the Image module (PIL)
import matplotlib.pyplot as plt
plt.imshow(f)
plt.show()위의 프로그램은 다음과 같은 출력을 생성합니다.

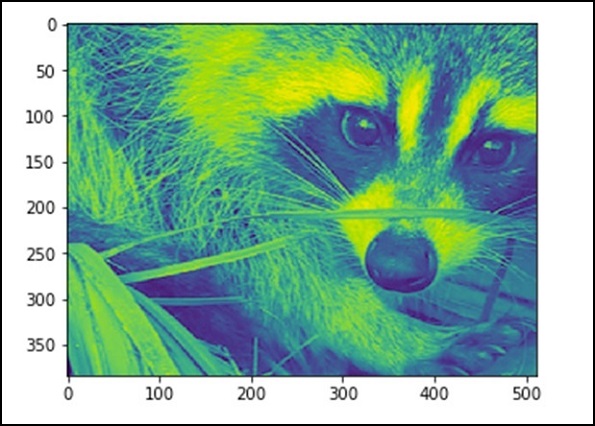
원시 형식의 모든 이미지는 행렬 형식의 숫자로 표시되는 색상 조합입니다. 기계는 그 숫자만으로 이미지를 이해하고 조작합니다. RGB는 널리 사용되는 표현 방법입니다.
위 이미지의 통계 정보를 살펴 보겠습니다.
from scipy import misc
face = misc.face(gray = False)
print face.mean(), face.max(), face.min()위의 프로그램은 다음과 같은 출력을 생성합니다.
110.16274388631184, 255, 0이제 이미지가 숫자로 만들어 졌으므로 숫자 값이 변경되면 원본 이미지가 변경됩니다. 이미지에 기하학적 변형을 수행해 보겠습니다. 기본적인 기하학적 작업은 자르기입니다.
from scipy import misc
face = misc.face(gray = True)
lx, ly = face.shape
# Cropping
crop_face = face[lx / 4: - lx / 4, ly / 4: - ly / 4]
import matplotlib.pyplot as plt
plt.imshow(crop_face)
plt.show()위의 프로그램은 다음과 같은 출력을 생성합니다.
아래에 설명 된대로 이미지를 거꾸로 뒤집는 것과 같은 몇 가지 기본 작업을 수행 할 수도 있습니다.
# up <-> down flip
from scipy import misc
face = misc.face()
flip_ud_face = np.flipud(face)
import matplotlib.pyplot as plt
plt.imshow(flip_ud_face)
plt.show()위의 프로그램은 다음과 같은 출력을 생성합니다.

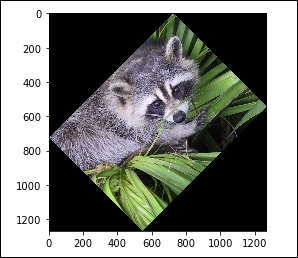
이 외에도 우리는 rotate() function, 지정된 각도로 이미지를 회전합니다.
# rotation
from scipy import misc,ndimage
face = misc.face()
rotate_face = ndimage.rotate(face, 45)
import matplotlib.pyplot as plt
plt.imshow(rotate_face)
plt.show()위의 프로그램은 다음과 같은 출력을 생성합니다.
필터
필터가 이미지 처리에 어떻게 도움이되는지 논의하겠습니다.
이미지 처리에서 필터링이란 무엇입니까?
필터링은 이미지를 수정하거나 향상시키는 기술입니다. 예를 들어 이미지를 필터링하여 특정 기능을 강조하거나 다른 기능을 제거 할 수 있습니다. 필터링으로 구현 된 이미지 처리 작업에는 Smoothing, Sharpening 및 Edge Enhancement가 포함됩니다.
필터링은 인접 연산으로, 출력 이미지의 특정 픽셀 값은 해당 입력 픽셀의 인접 픽셀 값에 일부 알고리즘을 적용하여 결정됩니다. 이제 SciPy ndimage를 사용하여 몇 가지 작업을 수행하겠습니다.
블러 링
블러 링은 이미지의 노이즈를 줄이기 위해 널리 사용됩니다. 필터 작업을 수행하고 이미지의 변화를 볼 수 있습니다. 다음 예를 살펴 보겠습니다.
from scipy import misc
face = misc.face()
blurred_face = ndimage.gaussian_filter(face, sigma=3)
import matplotlib.pyplot as plt
plt.imshow(blurred_face)
plt.show()위의 프로그램은 다음과 같은 출력을 생성합니다.

시그마 값은 5 단계의 흐림 수준을 나타냅니다. 시그마 값을 조정하여 이미지 품질의 변화를 확인할 수 있습니다. 흐림에 대한 자세한 내용은 → DIP (Digital Image Processing) Tutorial을 클릭하십시오.
가장자리 감지
가장자리 감지가 이미지 처리에 어떻게 도움이되는지 논의하겠습니다.
Edge Detection이란 무엇입니까?
가장자리 감지는 이미지 내에서 물체의 경계를 찾기위한 이미지 처리 기술입니다. 밝기의 불연속성을 감지하여 작동합니다. 에지 감지는 이미지 처리, 컴퓨터 비전 및 머신 비전과 같은 영역에서 이미지 분할 및 데이터 추출에 사용됩니다.
가장 일반적으로 사용되는 에지 감지 알고리즘은 다음과 같습니다.
- Sobel
- Canny
- Prewitt
- Roberts
- 퍼지 논리 방법
다음 예를 살펴 보겠습니다.
import scipy.ndimage as nd
import numpy as np
im = np.zeros((256, 256))
im[64:-64, 64:-64] = 1
im[90:-90,90:-90] = 2
im = ndimage.gaussian_filter(im, 8)
import matplotlib.pyplot as plt
plt.imshow(im)
plt.show()위의 프로그램은 다음과 같은 출력을 생성합니다.

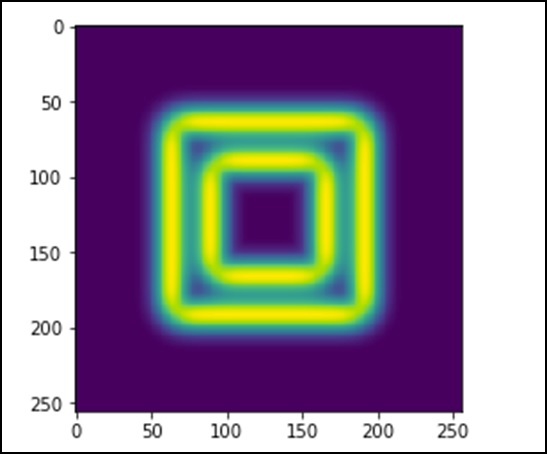
이미지는 정사각형 색상 블록처럼 보입니다. 이제 색상 블록의 가장자리를 감지합니다. 여기서 ndimage는Sobel이 작업을 수행합니다. 반면 NumPy는Hypot 두 개의 결과 행렬을 하나로 결합하는 함수입니다.
다음 예를 살펴 보겠습니다.
import scipy.ndimage as nd
import matplotlib.pyplot as plt
im = np.zeros((256, 256))
im[64:-64, 64:-64] = 1
im[90:-90,90:-90] = 2
im = ndimage.gaussian_filter(im, 8)
sx = ndimage.sobel(im, axis = 0, mode = 'constant')
sy = ndimage.sobel(im, axis = 1, mode = 'constant')
sob = np.hypot(sx, sy)
plt.imshow(sob)
plt.show()위의 프로그램은 다음과 같은 출력을 생성합니다.
그만큼 scipy.optimize package일반적으로 사용되는 몇 가지 최적화 알고리즘을 제공합니다. 이 모듈에는 다음과 같은 측면이 포함되어 있습니다.
다양한 알고리즘 (예 : BFGS, Nelder-Mead Simplex, Newton Conjugate Gradient, COBYLA 또는 SLSQP)을 사용하여 다변량 스칼라 함수 (minimize ())의 제한 및 제한 최소화
글로벌 (brute-force) 최적화 루틴 (예 : anneal (), basinhopping ())
최소 제곱 최소화 (leastsq ()) 및 곡선 피팅 (curve_fit ()) 알고리즘
스칼라 일 변량 함수 최소화 기 (minimize_scalar ()) 및 루트 파인더 (newton ())
다양한 알고리즘 (예 : 하이브리드 Powell, Levenberg-Marquardt 또는 Newton-Krylov와 같은 대규모 방법)을 사용하는 다변량 방정식 시스템 솔버 (root ())
다변량 스칼라 함수의 제한 및 제한 최소화
그만큼 minimize() function 다변량 스칼라 함수에 대한 제약없는 최소화 및 제약 된 최소화 알고리즘에 대한 공통 인터페이스를 제공합니다. scipy.optimize. 최소화 함수를 설명하기 위해 NN 변수의 Rosenbrock 함수를 최소화하는 문제를 고려하십시오.
$$f(x) = \sum_{i = 1}^{N-1} \:100(x_i - x_{i-1}^{2})$$
이 함수의 최소값은 0이며 xi = 1 일 때 달성됩니다.
Nelder–Mead Simplex 알고리즘
다음 예에서, minimal () 루틴은 Nelder-Mead simplex algorithm (method = 'Nelder-Mead')(method 매개 변수를 통해 선택됨). 다음 예를 살펴 보겠습니다.
import numpy as np
from scipy.optimize import minimize
def rosen(x):
x0 = np.array([1.3, 0.7, 0.8, 1.9, 1.2])
res = minimize(rosen, x0, method='nelder-mead')
print(res.x)위의 프로그램은 다음과 같은 출력을 생성합니다.
[7.93700741e+54 -5.41692163e+53 6.28769150e+53 1.38050484e+55 -4.14751333e+54]심플 렉스 알고리즘은 아마도 상당히 잘 작동하는 함수를 최소화하는 가장 간단한 방법 일 것입니다. 기능 평가 만 필요하며 간단한 최소화 문제에 적합한 선택입니다. 그러나 그래디언트 평가를 사용하지 않기 때문에 최소값을 찾는 데 더 오래 걸릴 수 있습니다.
최소값을 찾기 위해 함수 호출 만 필요한 또 다른 최적화 알고리즘은 Powell‘s method이는 minimal () 함수에서 method = 'powell'을 설정하여 사용할 수 있습니다.
최소 제곱
변수의 경계가있는 비선형 최소 제곱 문제를 풉니 다. 잔차 f (x) (n 개의 실수 변수의 m 차원 실수 함수)와 손실 함수 rho (s) (스칼라 함수)가 주어지면, least_squares는 비용 함수 F (x)의 국소 최솟값을 찾습니다. 다음 예를 살펴 보겠습니다.
이 예제에서는 독립 변수에 대한 경계가없는 최소 Rosenbrock 함수를 찾습니다.
#Rosenbrock Function
def fun_rosenbrock(x):
return np.array([10 * (x[1] - x[0]**2), (1 - x[0])])
from scipy.optimize import least_squares
input = np.array([2, 2])
res = least_squares(fun_rosenbrock, input)
print res잔차의 벡터 만 제공합니다. 이 알고리즘은 비용 함수를 잔차 제곱의 합으로 구성하여 Rosenbrock 함수를 제공합니다. 정확한 최소값은 x = [1.0,1.0]입니다.
위의 프로그램은 다음과 같은 출력을 생성합니다.
active_mask: array([ 0., 0.])
cost: 9.8669242910846867e-30
fun: array([ 4.44089210e-15, 1.11022302e-16])
grad: array([ -8.89288649e-14, 4.44089210e-14])
jac: array([[-20.00000015,10.],[ -1.,0.]])
message: '`gtol` termination condition is satisfied.'
nfev: 3
njev: 3
optimality: 8.8928864934219529e-14
status: 1
success: True
x: array([ 1., 1.])뿌리 찾기
SciPy에서 루트 찾기가 어떻게 도움이되는지 이해하겠습니다.
스칼라 함수
단일 변수 방정식이있는 경우 시도 할 수있는 4 개의 다른 근 찾기 알고리즘이 있습니다. 이러한 각 알고리즘에는 근이 예상되는 구간의 끝 점이 필요합니다 (함수가 부호를 변경하기 때문에). 일반적으로brentq 최선의 선택이지만 다른 방법은 특정 상황이나 학업 목적에 유용 할 수 있습니다.
고정 소수점 해결
함수의 0을 찾는 것과 밀접하게 관련된 문제는 함수의 고정 된 점을 찾는 문제입니다. 함수의 고정 소수점은 함수의 평가가 g (x) = x의 포인트를 반환하는 포인트입니다. 분명히 고정 된 지점ggf (x) = g (x) −x의 근입니다. 동등하게, 루트ffg (x) = f (x) + x의 고정 _ 점입니다. fixed_point 루틴은 다음을 사용하는 간단한 반복 방법을 제공합니다.Aitkens sequence acceleration 고정 소수점을 추정하기 위해 gg, 시작점이 주어진 경우.
방정식 세트
비선형 방정식 세트의 근을 찾는 방법은 다음과 같습니다. root() function. 여러 가지 방법을 사용할 수 있습니다.hybr (기본값) 및 lm은 각각 hybrid method of Powell 그리고 Levenberg-Marquardt method MINPACK에서.
다음 예에서는 단일 변수 초월 방정식을 고려합니다.
x2 + 2cos(x) = 0
그 뿌리는 다음과 같이 찾을 수 있습니다-
import numpy as np
from scipy.optimize import root
def func(x):
return x*2 + 2 * np.cos(x)
sol = root(func, 0.3)
print sol위의 프로그램은 다음과 같은 출력을 생성합니다.
fjac: array([[-1.]])
fun: array([ 2.22044605e-16])
message: 'The solution converged.'
nfev: 10
qtf: array([ -2.77644574e-12])
r: array([-3.34722409])
status: 1
success: True
x: array([-0.73908513])모든 통계 기능은 하위 패키지에 있습니다. scipy.stats 이러한 기능의 전체 목록은 다음을 사용하여 얻을 수 있습니다. info(stats)함수. 사용 가능한 랜덤 변수 목록은docstring통계 하위 패키지를 위해. 이 모듈에는 많은 확률 분포와 증가하는 통계 함수 라이브러리가 포함되어 있습니다.
각 단 변량 분포에는 다음 표에 설명 된대로 자체 하위 클래스가 있습니다.
| Sr. No. | 클래스 및 설명 |
|---|---|
| 1 | rv_continuous 서브 클래 싱을위한 일반 연속 랜덤 변수 클래스 |
| 2 | rv_discrete 서브 클래 싱을위한 일반 이산 랜덤 변수 클래스 |
| 삼 | rv_histogram 히스토그램으로 주어진 분포를 생성합니다. |
정규 연속 랜덤 변수
랜덤 변수 X가 임의의 값을 취할 수있는 확률 분포는 연속 랜덤 변수입니다. 위치 (loc) 키워드는 평균을 지정합니다. scale (scale) 키워드는 표준 편차를 지정합니다.
의 예로서 rv_continuous 수업, norm 객체는 그것으로부터 제네릭 메서드의 컬렉션을 상속하고이 특정 배포에 대한 세부 사항으로 완성합니다.
여러 지점에서 CDF를 계산하기 위해 목록 또는 NumPy 배열을 전달할 수 있습니다. 다음 예를 살펴 보겠습니다.
from scipy.stats import norm
import numpy as np
print norm.cdf(np.array([1,-1., 0, 1, 3, 4, -2, 6]))위의 프로그램은 다음과 같은 출력을 생성합니다.
array([ 0.84134475, 0.15865525, 0.5 , 0.84134475, 0.9986501 ,
0.99996833, 0.02275013, 1. ])분포의 중앙값을 찾기 위해 CDF의 역인 PPF (Percent Point Function)를 사용할 수 있습니다. 다음 예제를 사용하여 이해합시다.
from scipy.stats import norm
print norm.ppf(0.5)위의 프로그램은 다음과 같은 출력을 생성합니다.
0.0무작위 변량 시퀀스를 생성하려면 다음 예제에 표시된 size 키워드 인수를 사용해야합니다.
from scipy.stats import norm
print norm.rvs(size = 5)위의 프로그램은 다음과 같은 출력을 생성합니다.
array([ 0.20929928, -1.91049255, 0.41264672, -0.7135557 , -0.03833048])위의 출력은 재현 할 수 없습니다. 동일한 난수를 생성하려면 seed 함수를 사용하십시오.
균등 분포
uniform 함수를 사용하여 균일 분포를 생성 할 수 있습니다. 다음 예를 살펴 보겠습니다.
from scipy.stats import uniform
print uniform.cdf([0, 1, 2, 3, 4, 5], loc = 1, scale = 4)위의 프로그램은 다음과 같은 출력을 생성합니다.
array([ 0. , 0. , 0.25, 0.5 , 0.75, 1. ])이산 배포 구축
랜덤 샘플을 생성하고 관측 된 주파수를 확률과 비교해 보겠습니다.
이항 분포
의 예로서 rv_discrete class, binom object제네릭 메서드 컬렉션을 상속하고이 특정 배포에 대한 세부 정보로 완성합니다. 다음 예를 살펴 보겠습니다.
from scipy.stats import uniform
print uniform.cdf([0, 1, 2, 3, 4, 5], loc = 1, scale = 4)위의 프로그램은 다음과 같은 출력을 생성합니다.
array([ 0. , 0. , 0.25, 0.5 , 0.75, 1. ])기술 통계
Min, Max, Mean 및 Variance와 같은 기본 통계는 NumPy 배열을 입력으로 사용하고 각각의 결과를 반환합니다. 에서 사용할 수있는 몇 가지 기본 통계 기능scipy.stats package 다음 표에 설명되어 있습니다.
| Sr. No. | 기능 및 설명 |
|---|---|
| 1 | describe() 전달 된 배열의 여러 기술 통계를 계산합니다. |
| 2 | gmean() 지정된 축을 따라 기하 평균을 계산합니다. |
| 삼 | hmean() 지정된 축을 따라 조화 평균을 계산합니다. |
| 4 | kurtosis() 첨도를 계산합니다. |
| 5 | mode() 모달 값을 반환합니다. |
| 6 | skew() 데이터의 왜도를 테스트합니다. |
| 7 | f_oneway() 일원 분산 분석을 수행합니다. |
| 8 | iqr() 지정된 축을 따라 데이터의 사 분위수 범위를 계산합니다. |
| 9 | zscore() 표본 평균 및 표준 편차를 기준으로 표본에있는 각 값의 z 점수를 계산합니다. |
| 10 | sem() 입력 배열에있는 값의 평균 (또는 측정의 표준 오차)의 표준 오차를 계산합니다. |
이러한 기능 중 일부는 scipy.stats.mstats, 마스크 된 배열에서 작동합니다. 아래 주어진 예를 통해 이것을 이해합시다.
from scipy import stats
import numpy as np
x = np.array([1,2,3,4,5,6,7,8,9])
print x.max(),x.min(),x.mean(),x.var()위의 프로그램은 다음과 같은 출력을 생성합니다.
(9, 1, 5.0, 6.666666666666667)T- 테스트
SciPy에서 T-test가 어떻게 유용한 지 이해합시다.
ttest_1samp
하나의 점수 그룹 평균에 대한 T- 검정을 계산합니다. 이것은 독립 관측 값 'a'의 기대 값 (평균)이 주어진 모집단 평균과 같다는 귀무 가설에 대한 양면 검정입니다.popmean. 다음 예를 살펴 보겠습니다.
from scipy import stats
rvs = stats.norm.rvs(loc = 5, scale = 10, size = (50,2))
print stats.ttest_1samp(rvs,5.0)위의 프로그램은 다음과 같은 출력을 생성합니다.
Ttest_1sampResult(statistic = array([-1.40184894, 2.70158009]),
pvalue = array([ 0.16726344, 0.00945234]))두 샘플 비교
다음 예에는 두 개의 샘플이 있는데, 이는 동일하거나 다른 분포에서 나올 수 있으며 이러한 샘플이 동일한 통계 속성을 갖는지 테스트하려고합니다.
ttest_ind− 두 개의 독립적 인 점수 샘플의 평균에 대한 T- 검정을 계산합니다. 이것은 두 개의 독립 표본이 동일한 평균 (예상) 값을 갖는다는 귀무 가설에 대한 양측 검정입니다. 이 검정은 기본적으로 모집단의 분산이 동일하다고 가정합니다.
동일하거나 다른 모집단에서 두 개의 독립적 인 표본을 관찰하는 경우이 검정을 사용할 수 있습니다. 다음 예를 살펴 보겠습니다.
from scipy import stats
rvs1 = stats.norm.rvs(loc = 5,scale = 10,size = 500)
rvs2 = stats.norm.rvs(loc = 5,scale = 10,size = 500)
print stats.ttest_ind(rvs1,rvs2)위의 프로그램은 다음과 같은 출력을 생성합니다.
Ttest_indResult(statistic = -0.67406312233650278, pvalue = 0.50042727502272966)길이는 같지만 평균이 다른 새 배열로 동일하게 테스트 할 수 있습니다. 다른 값 사용loc 똑같이 테스트하십시오.
CSGraph는 Compressed Sparse Graph, 희소 행렬 표현에 기반한 빠른 그래프 알고리즘에 중점을 둡니다.
그래프 표현
우선 희소 그래프가 무엇이며 그래프 표현에서 어떻게 도움이되는지 이해하겠습니다.
희소 그래프 란 정확히 무엇입니까?
그래프는 노드 사이에 링크가있는 노드 모음 일뿐입니다. 그래프는 거의 모든 것을 나타낼 수 있습니다. 소셜 네트워크 연결, 각 노드는 사람이고 지인과 연결됩니다. 각 노드가 픽셀이고 인접 픽셀에 연결되는 이미지; 각 노드가 가장 가까운 이웃에 연결되는 고차원 분포의 점; 상상할 수있는 거의 모든 것.
그래프 데이터를 표현하는 매우 효율적인 방법 중 하나는 희소 행렬을 사용하는 것입니다. G라고 부르겠습니다. 행렬 G는 크기 N x N이고 G [i, j]는 노드 'i'와 노드 간의 연결 값을 제공합니다. '제이'. 희소 그래프는 대부분 0을 포함합니다. 즉, 대부분의 노드에는 연결이 거의 없습니다. 이 속성은 대부분의 관심 사례에서 사실로 밝혀졌습니다.
희소 그래프 하위 모듈의 생성은 다음을 포함하는 scikit-learn에서 사용 된 여러 알고리즘에 의해 동기가 부여되었습니다.
Isomap − 그래프에서 최단 경로를 찾아야하는 다양한 학습 알고리즘.
Hierarchical clustering − 최소 스패닝 트리를 기반으로하는 클러스터링 알고리즘.
Spectral Decomposition − 희소 그래프 라플라시안에 기반한 프로젝션 알고리즘.
구체적인 예로서 다음과 같은 무 방향 그래프를 나타내고 싶다고 가정 해보십시오.
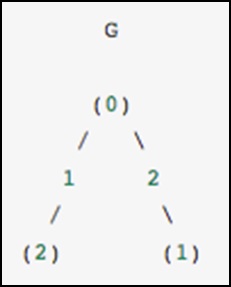
이 그래프에는 노드 0과 1이 가중치 2의 가장자리로 연결되고 노드 0과 2가 가중치 1의 가장자리로 연결되는 세 개의 노드가 있습니다. 다음 예제와 같이 조밀하고 마스킹 된 희소 표현을 구성 할 수 있습니다. , 무 방향 그래프는 대칭 행렬로 표현된다는 점을 명심하십시오.
G_dense = np.array([ [0, 2, 1],
[2, 0, 0],
[1, 0, 0] ])
G_masked = np.ma.masked_values(G_dense, 0)
from scipy.sparse import csr_matrix
G_sparse = csr_matrix(G_dense)
print G_sparse.data위의 프로그램은 다음과 같은 출력을 생성합니다.
array([2, 1, 2, 1])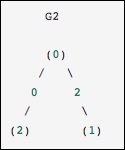
노드 0과 2가 가중치가 0 인 가장자리로 연결된다는 점을 제외하면 이전 그래프와 동일합니다. 이 경우, 위의 조밀 한 표현은 모호함으로 이어집니다. 0이 의미있는 값인 경우 가장자리가 아닌 것을 어떻게 표현할 수 있습니까? 이 경우 모호성을 제거하기 위해 마스크 또는 희소 표현을 사용해야합니다.
다음 예를 살펴 보겠습니다.
from scipy.sparse.csgraph import csgraph_from_dense
G2_data = np.array
([
[np.inf, 2, 0 ],
[2, np.inf, np.inf],
[0, np.inf, np.inf]
])
G2_sparse = csgraph_from_dense(G2_data, null_value=np.inf)
print G2_sparse.data위의 프로그램은 다음과 같은 출력을 생성합니다.
array([ 2., 0., 2., 0.])희소 그래프를 사용한 단어 래더
단어 사다리는 Lewis Carroll이 개발 한 게임으로, 각 단계에서 단일 문자를 변경하여 단어를 연결합니다. 예를 들면-
APE → APT → AIT → BIT → BIG → BAG → MAG → MAN
여기에서는 7 단계로 "APE"에서 "MAN"으로 이동하여 매번 한 문자를 변경합니다. 문제는-동일한 규칙을 사용하여이 단어들 사이의 짧은 경로를 찾을 수 있습니까? 이 문제는 당연히 희소 그래프 문제로 표현됩니다. 노드는 개별 단어에 해당하며 최대 한 글자 씩 다른 단어 사이에 연결을 만듭니다.
단어 목록 얻기
먼저 유효한 단어 목록을 얻어야합니다. Mac을 실행 중이며 Mac에는 다음 코드 블록에 지정된 위치에 단어 사전이 있습니다. 다른 아키텍처를 사용하는 경우 시스템 사전을 찾기 위해 약간 검색해야 할 수 있습니다.
wordlist = open('/usr/share/dict/words').read().split()
print len(wordlist)위의 프로그램은 다음과 같은 출력을 생성합니다.
235886이제 길이가 3 인 단어를 보려고하므로 올바른 길이의 단어 만 선택하겠습니다. 또한 대문자 (고유 명사)로 시작하거나 아포스트로피 및 하이픈과 같은 영숫자가 아닌 문자를 포함하는 단어도 제거합니다. 마지막으로 나중에 비교를 위해 모든 것이 소문자인지 확인합니다.
word_list = [word for word in word_list if len(word) == 3]
word_list = [word for word in word_list if word[0].islower()]
word_list = [word for word in word_list if word.isalpha()]
word_list = map(str.lower, word_list)
print len(word_list)위의 프로그램은 다음과 같은 출력을 생성합니다.
1135이제 1135 개의 유효한 3 글자 단어 목록이 있습니다 (정확한 숫자는 사용 된 특정 목록에 따라 변경 될 수 있음). 이러한 각 단어는 그래프에서 노드가되고, 각 단어 쌍과 관련된 노드를 연결하는 가장자리를 만들 것입니다.
import numpy as np
word_list = np.asarray(word_list)
word_list.dtype
word_list.sort()
word_bytes = np.ndarray((word_list.size, word_list.itemsize),
dtype = 'int8',
buffer = word_list.data)
print word_bytes.shape위의 프로그램은 다음과 같은 출력을 생성합니다.
(1135, 3)각 지점 간의 해밍 거리를 사용하여 연결된 단어 쌍을 결정합니다. 해밍 거리는 서로 다른 두 벡터 사이의 항목 비율을 측정합니다. 해밍 거리가 1 / N1 / N과 같은 두 단어입니다. 여기서 NN은 단어 래더에 연결된 문자 수입니다.
from scipy.spatial.distance import pdist, squareform
from scipy.sparse import csr_matrix
hamming_dist = pdist(word_bytes, metric = 'hamming')
graph = csr_matrix(squareform(hamming_dist < 1.5 / word_list.itemsize))거리를 비교할 때 부동 소수점 값에 대해 불안정 할 수 있으므로 동등성을 사용하지 않습니다. 부등식은 단어 목록의 두 항목이 동일하지 않는 한 원하는 결과를 생성합니다. 이제 그래프가 설정되었으므로 최단 경로 검색을 사용하여 그래프에서 두 단어 사이의 경로를 찾습니다.
i1 = word_list.searchsorted('ape')
i2 = word_list.searchsorted('man')
print word_list[i1],word_list[i2]위의 프로그램은 다음과 같은 출력을 생성합니다.
ape, man단어가 목록에 없으면 출력에 오류가 발생하므로 이러한 일치 여부를 확인해야합니다. 이제 우리에게 필요한 것은 그래프에서이 두 인덱스 사이의 최단 경로를 찾는 것입니다. 우리는 사용할 것입니다dijkstra’s 하나의 노드에 대한 경로를 찾을 수 있기 때문입니다.
from scipy.sparse.csgraph import dijkstra
distances, predecessors = dijkstra(graph, indices = i1, return_predecessors = True)
print distances[i2]위의 프로그램은 다음과 같은 출력을 생성합니다.
5.0따라서 우리는 '원숭이'와 '남자'사이의 최단 경로에 5 단계 만 포함되어 있음을 알 수 있습니다. 알고리즘이 반환 한 선행자를 사용하여이 경로를 재구성 할 수 있습니다.
path = []
i = i2
while i != i1:
path.append(word_list[i])
i = predecessors[i]
path.append(word_list[i1])
print path[::-1]i2]위의 프로그램은 다음과 같은 출력을 생성합니다.
['ape', 'ope', 'opt', 'oat', 'mat', 'man']그만큼 scipy.spatial package 포인트 세트의 삼각 측량, 보로 노이 다이어그램 및 볼록 껍질을 계산할 수 있습니다. Qhull library. 또한KDTree implementations 가장 가까운 인접 지점 쿼리 및 다양한 메트릭의 거리 계산을위한 유틸리티
들로네 삼각 분할
Delaunay Triangulation이 무엇이며 SciPy에서 어떻게 사용되는지 이해하겠습니다.
들로네 삼각 분할이란 무엇입니까?
수학 및 계산 기하학에서 주어진 세트에 대한 들로네 삼각 분할 P 평면에서 불연속 점의 수는 삼각 측량입니다. DT(P) 요점이 없도록 P DT (P)에서 삼각형의 외접원 안에 있습니다.
SciPy를 통해 동일한 계산을 할 수 있습니다. 다음 예를 살펴 보겠습니다.
from scipy.spatial import Delaunay
points = np.array([[0, 4], [2, 1.1], [1, 3], [1, 2]])
tri = Delaunay(points)
import matplotlib.pyplot as plt
plt.triplot(points[:,0], points[:,1], tri.simplices.copy())
plt.plot(points[:,0], points[:,1], 'o')
plt.show()위의 프로그램은 다음과 같은 출력을 생성합니다.

동일 평면상의 점
Coplanar Points가 무엇이며 SciPy에서 어떻게 사용되는지 이해하겠습니다.
동일 평면 상 포인트 란 무엇입니까?
동일 평면상의 점은 동일한 평면에있는 세 개 이상의 점입니다. 평면은 모든 방향으로 끝없이 확장되는 평평한 표면이라는 것을 상기하십시오. 일반적으로 수학 교과서에서 4 면체로 표시됩니다.
SciPy를 사용하여 어떻게 찾을 수 있는지 살펴 보겠습니다. 다음 예를 살펴 보겠습니다.
from scipy.spatial import Delaunay
points = np.array([[0, 0], [0, 1], [1, 0], [1, 1], [1, 1]])
tri = Delaunay(points)
print tri.coplanar위의 프로그램은 다음과 같은 출력을 생성합니다.
array([[4, 0, 3]], dtype = int32)이는 점 4가 삼각형 0과 정점 3 근처에 있지만 삼각 측량에 포함되지 않음을 의미합니다.
볼록 껍질
볼록 껍질이 무엇이며 SciPy에서 어떻게 사용되는지 이해하겠습니다.
볼록 껍질이란 무엇입니까?
수학에서 convex hull 또는 convex envelope 유클리드 평면 또는 유클리드 공간 (또는보다 일반적으로 실수 위의 아핀 공간)에있는 점 집합 X의 convex set X를 포함합니다.
자세히 이해하기 위해 다음 예를 고려해 보겠습니다.
from scipy.spatial import ConvexHull
points = np.random.rand(10, 2) # 30 random points in 2-D
hull = ConvexHull(points)
import matplotlib.pyplot as plt
plt.plot(points[:,0], points[:,1], 'o')
for simplex in hull.simplices:
plt.plot(points[simplex,0], points[simplex,1], 'k-')
plt.show()위의 프로그램은 다음과 같은 출력을 생성합니다.
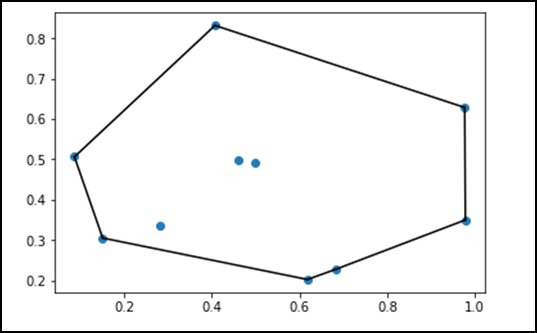
ODR은 Orthogonal Distance Regression, 회귀 연구에 사용됩니다. 기본 선형 회귀는 종종 두 변수 간의 관계를 추정하는 데 사용됩니다.y 과 x 그래프에 가장 적합한 선을 그립니다.
이를 위해 사용되는 수학적 방법은 다음과 같습니다. Least Squares, 각 포인트에 대한 제곱 오차의 합을 최소화하는 것을 목표로합니다. 여기서 핵심 질문은 각 포인트에 대한 오차 (잔차라고도 함)를 어떻게 계산합니까?
표준 선형 회귀에서 목표는 X 값에서 Y 값을 예측하는 것입니다. 따라서 Y 값의 오류를 계산하는 것이 현명합니다 (다음 이미지에서 회색 선으로 표시됨). 그러나 때때로 X와 Y 모두의 오류를 고려하는 것이 더 합리적입니다 (다음 이미지에서 빨간색 점선으로 표시됨).
예 : X의 측정 값이 불확실하거나 한 변수의 오류에 다른 변수에 초점을 맞추고 싶지 않을 때.
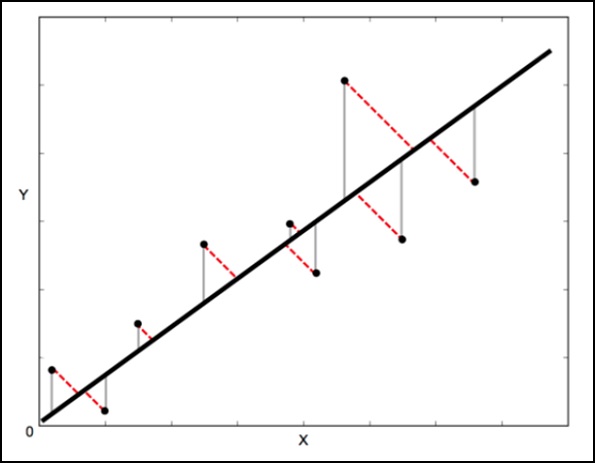
직교 거리 회귀 (ODR)는이를 수행 할 수있는 방법입니다 (이 컨텍스트에서 직교는 수직을 의미하므로 '수직'이 아닌 선에 수직으로 오류를 계산합니다).
일 변량 회귀를위한 scipy.odr 구현
다음 예제는 일 변량 회귀를위한 scipy.odr 구현을 보여줍니다.
import numpy as np
import matplotlib.pyplot as plt
from scipy.odr import *
import random
# Initiate some data, giving some randomness using random.random().
x = np.array([0, 1, 2, 3, 4, 5])
y = np.array([i**2 + random.random() for i in x])
# Define a function (quadratic in our case) to fit the data with.
def linear_func(p, x):
m, c = p
return m*x + c
# Create a model for fitting.
linear_model = Model(linear_func)
# Create a RealData object using our initiated data from above.
data = RealData(x, y)
# Set up ODR with the model and data.
odr = ODR(data, linear_model, beta0=[0., 1.])
# Run the regression.
out = odr.run()
# Use the in-built pprint method to give us results.
out.pprint()위의 프로그램은 다음과 같은 출력을 생성합니다.
Beta: [ 5.51846098 -4.25744878]
Beta Std Error: [ 0.7786442 2.33126407]
Beta Covariance: [
[ 1.93150969 -4.82877433]
[ -4.82877433 17.31417201
]]
Residual Variance: 0.313892697582
Inverse Condition #: 0.146618499389
Reason(s) for Halting:
Sum of squares convergence특별 패키지에서 사용할 수있는 기능은 브로드 캐스팅 및 자동 어레이 루핑을 따르는 범용 기능입니다.
가장 자주 사용되는 특수 기능 중 일부를 살펴 보겠습니다.
- 입방근 함수
- 지수 함수
- 상대 오차 지수 함수
- 로그 합계 지수 함수
- 램버트 기능
- 순열 및 조합 함수
- 감마 기능
이제 이러한 각 기능을 간략하게 이해하겠습니다.
입방근 함수
이 3 차 루트 함수의 구문은 – scipy.special.cbrt (x)입니다. 이것은 요소 별 큐브 루트를 가져옵니다.x.
다음 예를 살펴 보겠습니다.
from scipy.special import cbrt
res = cbrt([10, 9, 0.1254, 234])
print res위의 프로그램은 다음과 같은 출력을 생성합니다.
[ 2.15443469 2.08008382 0.50053277 6.16224015]지수 함수
지수 함수의 구문은 – scipy.special.exp10 (x)입니다. 이것은 10 ** x 요소를 계산합니다.
다음 예를 살펴 보겠습니다.
from scipy.special import exp10
res = exp10([2, 9])
print res위의 프로그램은 다음과 같은 출력을 생성합니다.
[1.00000000e+02 1.00000000e+09]상대 오차 지수 함수
이 함수의 구문은 – scipy.special.exprel (x)입니다. 상대 오류 지수 (exp (x)-1) / x를 생성합니다.
언제 x0에 가깝고 exp (x)는 1에 가까우므로 exp (x)-1의 수치 계산은 치명적인 정밀도 손실을 겪을 수 있습니다. 그런 다음 exprel (x)가 구현되어 정밀도 손실을 방지합니다.x 0에 가깝습니다.
다음 예를 살펴 보겠습니다.
from scipy.special import exprel
res = exprel([-0.25, -0.1, 0, 0.1, 0.25])
print res위의 프로그램은 다음과 같은 출력을 생성합니다.
[0.88479687 0.95162582 1. 1.05170918 1.13610167]로그 합계 지수 함수
이 함수의 구문은 – scipy.special.logsumexp (x)입니다. 입력 요소의 지수 합계 로그를 계산하는 데 도움이됩니다.
다음 예를 살펴 보겠습니다.
from scipy.special import logsumexp
import numpy as np
a = np.arange(10)
res = logsumexp(a)
print res위의 프로그램은 다음과 같은 출력을 생성합니다.
9.45862974443램버트 기능
이 함수의 구문은 – scipy.special.lambertw (x)입니다. Lambert W 함수라고도합니다. Lambert W 함수 W (z)는 w * exp (w)의 역함수로 정의됩니다. 즉, W (z)의 값은 복소수 z에 대해 z = W (z) * exp (W (z))가됩니다.
Lambert W 함수는 분기가 무한히 많은 다중 값 함수입니다. 각 분기는 방정식 z = w exp (w)의 개별 솔루션을 제공합니다. 여기서 분기는 정수 k로 인덱싱됩니다.
다음 예를 살펴 보겠습니다. 여기서 Lambert W 함수는 w exp (w)의 역입니다.
from scipy.special import lambertw
w = lambertw(1)
print w
print w * np.exp(w)위의 프로그램은 다음과 같은 출력을 생성합니다.
(0.56714329041+0j)
(1+0j)순열 및 조합
순열과 조합을 명확하게 이해하기 위해 별도로 논의하겠습니다.
Combinations− 조합 함수의 구문은 – scipy.special.comb (N, k)입니다. 다음 예를 살펴 보겠습니다.
from scipy.special import comb
res = comb(10, 3, exact = False,repetition=True)
print res위의 프로그램은 다음과 같은 출력을 생성합니다.
220.0Note− 정확한 = False 경우에만 배열 인수가 허용됩니다. k> N, N <0 또는 k <0이면 0이 반환됩니다.
Permutations− 조합 함수의 구문은 – scipy.special.perm (N, k)입니다. 한 번에 k를 취한 N 개의 순열, 즉 N의 k 순열. 이것은 "부분 순열"이라고도합니다.
다음 예를 살펴 보겠습니다.
from scipy.special import perm
res = perm(10, 3, exact = True)
print res위의 프로그램은 다음과 같은 출력을 생성합니다.
720감마 기능
감마 함수는 자연수 'n'에 대해 z * gamma (z) = gamma (z + 1) 및 gamma (n + 1) = n!이므로 일반화 계승이라고도합니다.
조합 함수의 구문은 – scipy.special.gamma (x)입니다. 한 번에 k를 취한 N 개의 순열, 즉 N의 k 순열. 이것은 "부분 순열"이라고도합니다.
조합 함수의 구문은 – scipy.special.gamma (x)입니다. 한 번에 k를 취한 N 개의 순열, 즉 N의 k 순열. 이것은 "부분 순열"이라고도합니다.
from scipy.special import gamma
res = gamma([0, 0.5, 1, 5])
print res위의 프로그램은 다음과 같은 출력을 생성합니다.
[inf 1.77245385 1. 24.]