조합형 MOS 로직 회로
여러 입력 변수에 대해 부울 연산을 수행하고 입력의 부울 함수로 출력을 결정하는 조합 논리 회로 또는 게이트는 모든 디지털 시스템의 기본 구성 요소입니다. 2 입력 NAND 및 NOR 게이트와 같은 간단한 회로 구성을 검토 한 다음 분석을보다 일반적인 다중 입력 회로 구조 사례로 확장합니다.
다음으로 CMOS 논리 회로가 유사한 방식으로 제시됩니다. nMOS 공핍 부하 로직과 CMOS 로직 회로의 유사점과 차이점을 강조하고 CMOS 게이트의 장점을 예로 들어 설명하겠습니다. 가장 일반적인 형태로 부울 기능을 수행하는 조합 논리 회로 또는 게이트는 그림에 표시된대로 다중 입력, 단일 출력 시스템으로 표현 될 수 있습니다.
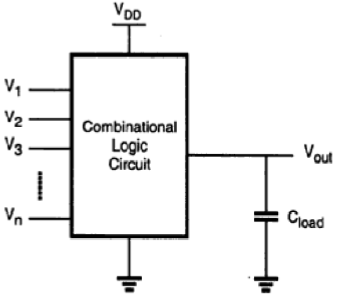
접지 전위를 기준으로하는 노드 전압은 모든 입력 변수를 나타냅니다. 양의 논리 규칙을 사용하면 "1"의 부울 (또는 논리) 값은 VDD의 고전압으로 표시 될 수 있고 "0"의 부울 (또는 논리) 값은 0의 저전압으로 표시 될 수 있습니다. 출력 노드 에는 회로에있는 기생 장치의 결합 된 커패시턴스를 나타내는 커패시턴스 C L 이로드됩니다.
CMOS 논리 회로
CMOS 2 입력 NOR 게이트
회로는 병렬로 연결된 n-net과 직렬로 연결된 보완 p-net으로 구성됩니다. 입력 전압 V X 및 V Y 는 하나의 nMOS 및 하나의 pMOS 트랜지스터의 게이트에 적용됩니다.
입력 중 하나 또는 모두가 높을 때, 즉 n-net이 출력 노드와 접지 사이에 전도 경로를 생성 할 때 p-net이 차단됩니다. 두 입력 전압이 모두 낮 으면, 즉 n-net이 차단되면 p-net은 출력 노드와 공급 전압 사이에 전도 경로를 생성합니다.
주어진 입력 조합에 대해 보완 회로 구조는 출력이 V DD에 연결되거나 저 저항 경로를 통해 접지에 연결되고 V DD 와 접지 사이의 DC 전류 경로가 입력 조합에 대해 설정되지 않도록합니다. CMOS의 출력 전압, 두 개의 입력 NOR 게이트는 V OL = 0 의 로직 로우 전압과 V OH = V DD 의 로직 하이 전압을 얻습니다 . 스위칭 임계 전압 V th 의 방정식 은 다음과 같습니다.
$$ V_ {th} \ 왼쪽 (NOR2 \ 오른쪽) = \ frac {V_ {T, n} + \ frac {1} {2} \ sqrt {\ frac {k_ {p}} {k_ {n}} \ 왼쪽 (V_ {DD}-\ left | V_ {T, p} \ right | \ right)}} {1+ \ frac {1} {2} \ sqrt {\ frac {k_ {p}} {k_ {n }}}} $$
CMOS 2 입력 NOR 게이트의 레이아웃
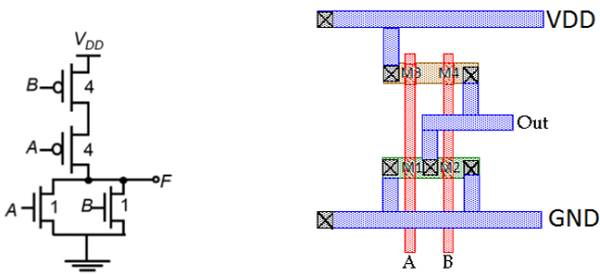
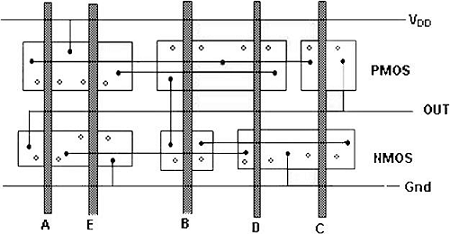
그림은 단일 레이어 금속 및 단일 레이어 폴리 실리콘을 사용하는 CMOS 2 입력 NOR 게이트의 샘플 레이아웃을 보여줍니다. 이 레이아웃의 특징은-
- 각 입력에 대한 단일 수직 폴리 라인
- N 및 P 장치 각각에 대한 단일 활성 모양
- 수평으로 달리는 금속 버스
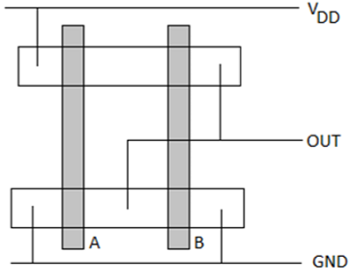
CMOS N0R2 게이트의 스틱 다이어그램은 아래 그림에 나와 있습니다. 레이아웃에 직접 해당하지만 W 및 L 정보는 포함하지 않습니다. 확산 영역은 직사각형으로 표시되고 금속 연결부와 실선 및 원은 각각 접점을 나타내고 크로스 해칭 된 스트립은 폴리 실리콘 열을 나타냅니다. 스틱 다이어그램은 최적의 레이아웃 토폴로지를 계획하는 데 유용합니다.
CMOS 2 입력 NAND 게이트
두 개의 입력 CMOS NAND 게이트의 회로도는 아래 그림에 나와 있습니다.
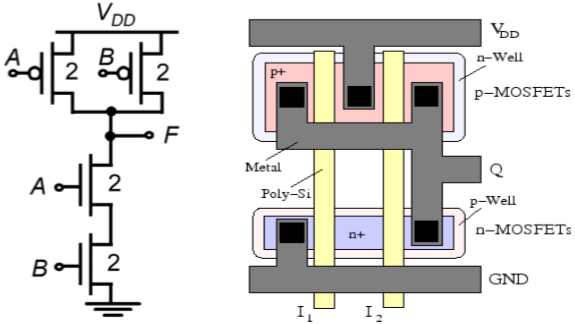
회로의 작동 원리는 CMOS 2 입력 NOR 작동의 정확한 이중입니다. 두 개의 직렬 연결된 nMOS 트랜지스터로 구성된 n – net은 두 입력 전압이 모두 로직 하이 인 경우 출력 노드와 접지 사이에 전도 경로를 생성합니다. p-net에서 병렬로 연결된 pMOS 트랜지스터는 모두 꺼집니다.
다른 모든 입력 조합의 경우 pMOS 트랜지스터 중 하나 또는 둘 모두가 켜지고 p – net이 차단되어 출력 노드와 전원 공급 장치 전압 사이에 전류 경로가 생성됩니다. 이 게이트의 스위칭 임계 값은 다음과 같이 구합니다.
$$ V_ {th} \ left (NAND2 \ right) = \ frac {V_ {T, n} +2 \ sqrt {\ frac {k_ {p}} {k_ {n}} \ left (V_ {DD}- \ 왼쪽 | V_ {T, p} \ 오른쪽 | \ 오른쪽)}} {1 + 2 \ sqrt {\ frac {k_ {p}} {k_ {n}}}} $$
이 레이아웃의 특징은 다음과 같습니다-
- 입력을위한 단일 폴리 실리콘 라인은 N 및 P 활성 영역 모두에서 수직으로 실행됩니다.
- 단일 활성 형태는 nMOS 장치와 두 pMOS 장치를 모두 구축하는 데 사용됩니다.
- 파워 버스는 레이아웃의 상단과 하단에 수평으로 실행됩니다.
- 출력 와이어는 수평으로 연결되어 인접 회로에 쉽게 연결할 수 있습니다.
복잡한 논리 회로
NMOS 공핍 부하 복잡한 논리 게이트
여러 입력 변수의 복잡한 기능을 구현하기 위해 NOR 및 NAND 용으로 개발 된 기본 회로 구조 및 설계 원리를 복잡한 논리 게이트로 확장 할 수 있습니다. 적은 수의 트랜지스터를 사용하여 복잡한 논리 기능을 구현할 수있는 능력은 nMOS 및 CMOS 논리 회로의 가장 매력적인 기능 중 하나입니다. 다음 부울 함수를 예로 고려하십시오.
$$ \ overline {Z = P \ 왼쪽 (S + T \ 오른쪽) + QR} $$
이 기능을 실현하는 데 사용되는 nMOS 공핍 부하 복합 논리 게이트가 그림에 나와 있습니다. 이 그림에서 3 개의 드라이버 트랜지스터의 왼쪽 nMOS 드라이버 분기는 논리 기능 P (S + T)를 수행하는 데 사용되며 오른쪽 분기는 QR 기능을 수행합니다. 두 분기를 병렬로 연결하고 출력 노드와 공급 전압 사이에 부하 트랜지스터를 배치하여VDD,주어진 복잡한 함수를 얻습니다. 각 입력 변수는 하나의 드라이버에만 할당됩니다.
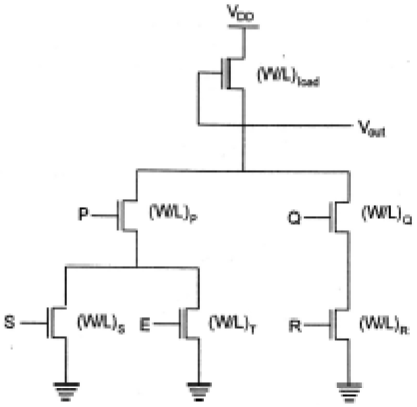
회로 토폴로지 검사는 풀다운 네트워크의 단순한 설계 원칙을 제공합니다.
- OR 연산은 병렬 연결된 드라이버에 의해 수행됩니다.
- AND 연산은 직렬 연결된 드라이버에 의해 수행됩니다.
- 반전은 MOS 회로 작동의 특성에 의해 제공됩니다.
기능을 실현하는 회로에서 모든 입력 변수가 로직 하이이면 등가 드라이버 (W/L) 5 개의 nMOS 트랜지스터로 구성된 풀다운 네트워크의 비율은
$$ \ frac {W} {L} = \ frac {1} {\ frac {1} {\ left (W / L \ right) Q} + \ frac {1} {\ left (W / L \ right) R}} + \ frac {1} {\ frac {1} {\ left (W / L \ right) P} + \ frac {1} {\ left (W / L \ right) S + \ left (W / L \ 오른쪽) Q}} $$
복잡한 CMOS 로직 게이트
n-net 또는 풀다운 네트워크의 실현은 nMOS 공핍 부하 복잡한 논리 게이트에 대해 조사 된 것과 동일한 기본 설계 원칙을 기반으로합니다. pMOS 풀업 네트워크는 n-net의 이중 네트워크 여야합니다.
이는 nMOS 네트워크의 모든 병렬 연결이 pMOS 네트워크의 직렬 연결에 해당하고 nMOS 네트워크의 모든 직렬 연결이 pMOS 네트워크의 병렬 연결에 해당함을 의미합니다. 이 그림은 n-net (풀다운) 그래프에서 이중 p-net (풀업) 그래프의 간단한 구성을 보여줍니다.
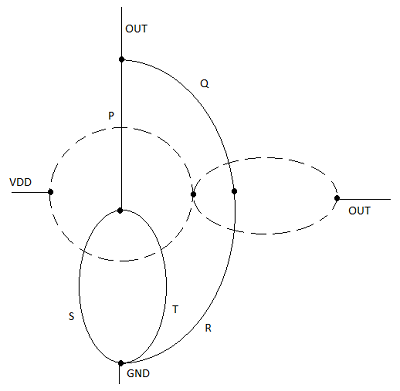
풀다운 네트워크의 각 드라이버 트랜지스터는 ai로 표시되고 각 노드는 풀다운 그래프에서 정점으로 표시됩니다. 다음으로 풀 그래프의 각 제한된 영역 내에 새 정점이 생성되고 풀다운 그래프의 각 가장자리를 한 번만 교차하는 가장자리로 인접한 정점이 연결됩니다. 이 새로운 그래프는 풀업 네트워크를 보여줍니다.
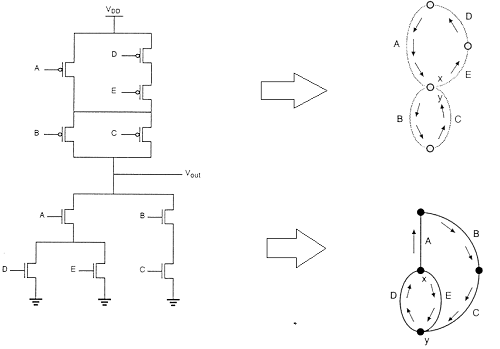
오일러 그래프 방법을 사용한 레이아웃 기법
그림은 CMOS 게이트에 대해 매우 최적화되지 않은 레이아웃을 제공하는 임의의 게이트 순서로 수행 된 복잡한 기능의 CMOS 구현과 해당 스틱 다이어그램을 보여줍니다.
이 경우, 폴리 실리콘 컬럼 사이의 분리는 그 사이에서 확산-확산 분리를 허용해야합니다. 이것은 확실히 상당한 양의 추가 실리콘 영역을 소비합니다.
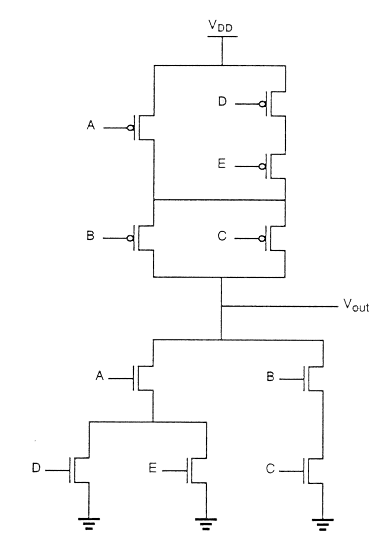
오일러 경로를 사용하여 최적의 레이아웃을 얻을 수 있습니다. 오일러 경로는 그래프의 각 가장자리 (분기)를 정확히 한 번 횡단하는 중단없는 경로로 정의됩니다. 입력 순서가 동일한 풀다운 트리 그래프와 풀업 트리 그래프에서 오일러 경로를 찾습니다.