Scikit Learn - wsparcie maszyn wektorowych

W tym rozdziale omówiono metodę uczenia maszynowego określaną jako maszyny wektorów nośnych (SVM).

Wprowadzenie

Maszyny wektorów nośnych (SVM) to potężne, ale elastyczne metody nadzorowanego uczenia maszynowego używane do klasyfikacji, regresji i wykrywania wartości odstających. SVM są bardzo wydajne w dużych przestrzeniach wymiarowych i generalnie są używane w problemach klasyfikacyjnych. Maszyny SVM są popularne i wydajne w pamięci, ponieważ wykorzystują podzbiór punktów szkoleniowych w funkcji decyzyjnej.

Głównym celem maszyn SVM jest podzielenie zbiorów danych na liczbę klas w celu znalezienia pliku maximum marginal hyperplane (MMH) co można zrobić w dwóch następujących krokach -

Maszyny wektorów pomocniczych będą najpierw iteracyjnie generować hiperpłaszczyzny, które w najlepszy sposób oddziela klasy.
Następnie wybierze hiperpłaszczyznę, która prawidłowo segreguje klasy.

Oto kilka ważnych pojęć w SVM -

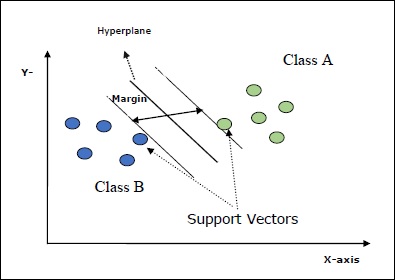
Support Vectors- Można je zdefiniować jako punkty danych, które znajdują się najbliżej hiperpłaszczyzny. Wektory pomocnicze pomagają w określeniu linii oddzielającej.
Hyperplane - Płaszczyzna decyzyjna lub przestrzeń, która dzieli zbiór obiektów o różnych klasach.
Margin - Odstęp między dwoma liniami w punktach danych szafy różnych klas nazywany jest marginesem.

Poniższe diagramy dają wgląd w te koncepcje SVM -

SVM w Scikit-learn obsługuje zarówno rzadkie, jak i gęste wektory próbek jako dane wejściowe.

Klasyfikacja SVM

Scikit-learn zapewnia trzy klasy, a mianowicie SVC, NuSVC i LinearSVC który może wykonać klasyfikację wieloklasową.

SVC

Jest to klasyfikacja wektora nośnika C, na której opiera się implementacja libsvm. Moduł używany przez scikit-learn tosklearn.svm.SVC. Ta klasa obsługuje obsługę wielu klas zgodnie ze schematem jeden na jeden.

Parametry

Poniższa tabela zawiera parametry używane przez sklearn.svm.SVC klasa -

Sr.No	Parametr i opis
1	C - float, opcjonalne, domyślnie = 1.0 Jest to parametr kary składnika błędu.
2	kernel - string, opcjonalny, domyślny = 'rbf' Ten parametr określa typ jądra, które ma być użyte w algorytmie. możemy wybrać dowolną spośród,‘linear’, ‘poly’, ‘rbf’, ‘sigmoid’, ‘precomputed’. Domyślna wartość jądra to‘rbf’.
3	degree - int, opcjonalne, domyślnie = 3 Reprezentuje stopień funkcji jądra „poli” i będzie ignorowany przez wszystkie inne jądra.
4	gamma - {'scale', 'auto'} lub float, Jest to współczynnik jądra dla jąder „rbf”, „poly” i „sigmoid”.
5	optinal default - = 'skala' Jeśli wybierzesz wartość domyślną, tj. Gamma = 'scale', wówczas wartość gamma, która ma być używana przez SVC, wynosi 1 / (_ ∗. ()). Z drugiej strony, jeśli gamma = 'auto', używa 1 / _.
6	coef0 - float, opcjonalne, domyślnie = 0,0 Niezależny termin w funkcji jądra, który ma znaczenie tylko w „poli” i „sigmoidzie”.
7	tol - float, opcjonalne, domyślnie = 1.e-3 Ten parametr reprezentuje kryterium zatrzymania dla iteracji.
8	shrinking - Boolean, opcjonalne, domyślnie = True Ten parametr określa, czy chcemy używać kurczącej się heurystyki, czy nie.
9	verbose - Boolean, domyślnie: false Włącza lub wyłącza pełne informacje wyjściowe. Jego domyślna wartość to false.
10	probability - logiczna, opcjonalna, domyślna = prawda Ten parametr włącza lub wyłącza oszacowania prawdopodobieństwa. Wartość domyślna to false, ale musi być włączona przed wywołaniem fit.
11	max_iter - int, opcjonalne, domyślnie = -1 Jak sugeruje nazwa, reprezentuje maksymalną liczbę iteracji w rozwiązaniu. Wartość -1 oznacza, że nie ma ograniczenia liczby iteracji.
12	cache_size - pływak, opcjonalnie Ten parametr określa rozmiar pamięci podręcznej jądra. Wartość będzie w MB (megabajtach).
13	random_state - int, instancja RandomState lub None, opcjonalne, default = none Ten parametr reprezentuje ziarno wygenerowanej liczby pseudolosowej, która jest używana podczas tasowania danych. Poniżej znajdują się opcje - int- W tym przypadku random_state jest ziarnem używanym przez generator liczb losowych. RandomState instance - W tym przypadku random_state jest generatorem liczb losowych. None - W tym przypadku generatorem liczb losowych jest instancja RandonState używana przez np.random.
14	class_weight - {dict, 'balance'}, opcjonalnie Ten parametr ustawi parametr C klasy j na _ℎ [] ∗ dla SVC. Jeśli użyjemy opcji domyślnej, oznacza to, że wszystkie klasy mają mieć wagę jeden. Z drugiej strony, jeśli wybierzeszclass_weight:balanced, użyje wartości y do automatycznego dostosowania wag.
15	decision_function_shape - ovo ',' ovr ', default =' ovr ' Ten parametr zdecyduje, czy algorytm zwróci ‘ovr’ (jeden vs reszta) funkcja decyzyjna kształtu, podobnie jak wszystkie inne klasyfikatory lub oryginał ovo(jeden vs jeden) funkcja decyzyjna libsvm.
16	break_ties - boolean, opcjonalne, domyślnie = false True - Prognoza przełamie więzi zgodnie z wartościami ufności funkcji decyzyjnej False - Przewidywanie zwróci pierwszą klasę z remisujących klas.

Atrybuty

Poniższa tabela zawiera atrybuty używane przez sklearn.svm.SVC klasa -

Sr.No	Atrybuty i opis
1	support_ - podobny do tablicy, kształt = [n_SV] Zwraca indeksy wektorów nośnych.
2	support_vectors_ - podobny do tablicy, kształt = [n_SV, n_features] Zwraca wektory nośne.
3	n_support_ - podobne do tablicy, dtype = int32, shape = [n_class] Reprezentuje liczbę wektorów nośnych dla każdej klasy.
4	dual_coef_ - tablica, kształt = [n_class-1, n_SV] Są to współczynniki wektorów nośnych w funkcji decyzji.
5	coef_ - tablica, kształt = [n_class * (n_class-1) / 2, n_features] Ten atrybut, dostępny tylko w przypadku jądra liniowego, podaje wagę przypisaną cechom.
6	intercept_ - tablica, kształt = [n_class * (n_class-1) / 2] Reprezentuje niezależny termin (stała) w funkcji decyzyjnej.
7	fit_status_ - wew Wyjście będzie wynosić 0, jeśli zostanie prawidłowo zamontowane. Wyjście byłoby 1, jeśli jest nieprawidłowo zamontowane.
8	classes_ - tablica kształtu = [n_classes] Podaje etykiety klas.

Implementation Example

Podobnie jak inne klasyfikatory, SVC również musi być wyposażony w następujące dwie tablice -

Tablica Xtrzymanie próbek treningowych. Ma rozmiar [n_samples, n_features].
Tablica Ytrzymanie wartości docelowych, tj. etykiet klas dla próbek uczących. Ma rozmiar [n_samples].

Następujące użycie skryptu Pythona sklearn.svm.SVC klasa -

import numpy as np
X = np.array([[-1, -1], [-2, -1], [1, 1], [2, 1]])
y = np.array([1, 1, 2, 2])
from sklearn.svm import SVC
SVCClf = SVC(kernel = 'linear',gamma = 'scale', shrinking = False,)
SVCClf.fit(X, y)

Output

SVC(C = 1.0, cache_size = 200, class_weight = None, coef0 = 0.0,
   decision_function_shape = 'ovr', degree = 3, gamma = 'scale', kernel = 'linear',
   max_iter = -1, probability = False, random_state = None, shrinking = False,
   tol = 0.001, verbose = False)

Example

Teraz, po dopasowaniu, możemy uzyskać wektor wagi za pomocą następującego skryptu w Pythonie -

SVCClf.coef_

Output

array([[0.5, 0.5]])

Example

Podobnie możemy uzyskać wartość innych atrybutów w następujący sposób -

SVCClf.predict([[-0.5,-0.8]])

Output

array([1])

Example

SVCClf.n_support_

Output

array([1, 1])

Example

SVCClf.support_vectors_

Output

array(
   [
      [-1., -1.],
      [ 1., 1.]
   ]
)

Example

SVCClf.support_

Output

array([0, 2])

Example

SVCClf.intercept_

Output

array([-0.])

Example

SVCClf.fit_status_

Output

NuSVC

NuSVC to klasyfikacja wektorów wsparcia Nu. Jest to kolejna klasa udostępniana przez scikit-learn, która może przeprowadzić klasyfikację wieloklasową. Jest podobny do SVC, ale NuSVC akceptuje nieco inne zestawy parametrów. Parametr różniący się od SVC jest następujący -

nu - float, opcjonalne, domyślnie = 0,5

Reprezentuje górną granicę ułamka błędów uczących i dolną granicę ułamka wektorów nośnych. Jego wartość powinna zawierać się w przedziale (o, 1].

Pozostałe parametry i atrybuty są takie same jak w SVC.

Przykład implementacji

Możemy zaimplementować ten sam przykład używając sklearn.svm.NuSVC klasa również.

import numpy as np
X = np.array([[-1, -1], [-2, -1], [1, 1], [2, 1]])
y = np.array([1, 1, 2, 2])
from sklearn.svm import NuSVC
NuSVCClf = NuSVC(kernel = 'linear',gamma = 'scale', shrinking = False,)
NuSVCClf.fit(X, y)

Wynik

NuSVC(cache_size = 200, class_weight = None, coef0 = 0.0,
   decision_function_shape = 'ovr', degree = 3, gamma = 'scale', kernel = 'linear',
   max_iter = -1, nu = 0.5, probability = False, random_state = None,
   shrinking = False, tol = 0.001, verbose = False)

Możemy otrzymać wyniki pozostałych atrybutów, tak jak w przypadku SVC.

LinearSVC

Jest to liniowa klasyfikacja wektorów nośnych. Jest podobny do SVC, w którym kernel = 'linear'. Różnica między nimi polega na tymLinearSVC zaimplementowano w kategoriach liblinear, natomiast SVC w libsvm. To jest powódLinearSVCma większą elastyczność w wyborze kar i funkcji strat. Skaluje się również lepiej do dużej liczby próbek.

Jeśli mówimy o jego parametrach i atrybutach, to nie obsługuje ‘kernel’ ponieważ zakłada się, że jest liniowy, a także brakuje mu niektórych atrybutów, takich jak support_, support_vectors_, n_support_, fit_status_ i, dual_coef_.

Jednak obsługuje penalty i loss parametry w następujący sposób -

penalty − string, L1 or L2(default = ‘L2’)

Ten parametr służy do określenia normy (L1 lub L2) używanej w penalizacji (regularyzacji).
loss − string, hinge, squared_hinge (default = squared_hinge)

Reprezentuje funkcję straty, gdzie „zawias” to standardowa strata SVM, a „kwadratowy_zawias” to kwadrat utraty zawiasu.

Przykład implementacji

Następujące użycie skryptu Pythona sklearn.svm.LinearSVC klasa -

from sklearn.svm import LinearSVC
from sklearn.datasets import make_classification
X, y = make_classification(n_features = 4, random_state = 0)
LSVCClf = LinearSVC(dual = False, random_state = 0, penalty = 'l1',tol = 1e-5)
LSVCClf.fit(X, y)

Wynik

LinearSVC(C = 1.0, class_weight = None, dual = False, fit_intercept = True,
   intercept_scaling = 1, loss = 'squared_hinge', max_iter = 1000,
   multi_class = 'ovr', penalty = 'l1', random_state = 0, tol = 1e-05, verbose = 0)

Przykład

Teraz, po dopasowaniu, model może przewidywać nowe wartości w następujący sposób -

LSVCClf.predict([[0,0,0,0]])

Wynik

[1]

Przykład

W powyższym przykładzie możemy uzyskać wektor wagi za pomocą następującego skryptu w Pythonie -

LSVCClf.coef_

Wynik

[[0. 0. 0.91214955 0.22630686]]

Przykład

Podobnie możemy uzyskać wartość przechwycenia za pomocą następującego skryptu w Pythonie -

LSVCClf.intercept_

Wynik

[0.26860518]

Regresja za pomocą SVM

Jak wspomniano wcześniej, SVM jest używana zarówno w przypadku problemów związanych z klasyfikacją, jak i regresją. Metodę klasyfikacji wektorów nośnych (SVC) opracowaną przez Scikit-learn można również rozszerzyć w celu rozwiązania problemów regresji. Ta rozszerzona metoda nosi nazwę regresji wektora nośnego (SVR).

Podstawowe podobieństwo między SVM i SVR

Model utworzony przez SVC zależy tylko od podzbioru danych uczących. Czemu? Ponieważ funkcja kosztu budowy modelu nie dba o treningowe punkty danych, które znajdują się poza marginesem.

Natomiast model stworzony przez SVR (regresja wektora wsparcia) również zależy tylko od podzbioru danych uczących. Czemu? Ponieważ funkcja kosztu tworzenia modelu ignoruje wszelkie punkty danych szkoleniowych zbliżone do prognozy modelu.

Scikit-learn zapewnia trzy klasy, a mianowicie SVR, NuSVR and LinearSVR jako trzy różne implementacje SVR.

SVR

Jest to regresja wektorowa obsługująca Epsilon, której implementacja opiera się na libsvm. W przeciwieństwie doSVC W modelu są dwa dowolne parametry, a mianowicie ‘C’ i ‘epsilon’.

epsilon - float, opcjonalne, domyślnie = 0,1

Reprezentuje epsilon w modelu epsilon-SVR i określa rurkę epsilon, w której nie jest powiązana żadna kara w funkcji utraty treningu z punktami przewidywanymi w odległości epsilon od rzeczywistej wartości.

Pozostałe parametry i atrybuty są podobne do tych, których używaliśmy w SVC.

Przykład implementacji

Następujące użycie skryptu Pythona sklearn.svm.SVR klasa -

from sklearn import svm
X = [[1, 1], [2, 2]]
y = [1, 2]
SVRReg = svm.SVR(kernel = ’linear’, gamma = ’auto’)
SVRReg.fit(X, y)

Wynik

SVR(C = 1.0, cache_size = 200, coef0 = 0.0, degree = 3, epsilon = 0.1, gamma = 'auto',
   kernel = 'linear', max_iter = -1, shrinking = True, tol = 0.001, verbose = False)

Przykład

Teraz, po dopasowaniu, możemy uzyskać wektor wagi za pomocą następującego skryptu w Pythonie -

SVRReg.coef_

Wynik

array([[0.4, 0.4]])

Przykład

Podobnie możemy uzyskać wartość innych atrybutów w następujący sposób -

SVRReg.predict([[1,1]])

Wynik

array([1.1])

Podobnie możemy również uzyskać wartości innych atrybutów.

NuSVR

NuSVR to regresja wektora wsparcia Nu. To jest jak NuSVC, ale NuSVR używa parametrunukontrolować liczbę wektorów nośnych. A ponadto, w przeciwieństwie do NuSVC, gdzienu zastąpiony parametr C, tutaj zastępuje epsilon.

Przykład implementacji

Następujące użycie skryptu Pythona sklearn.svm.SVR klasa -

from sklearn.svm import NuSVR
import numpy as np
n_samples, n_features = 20, 15
np.random.seed(0)
y = np.random.randn(n_samples)
X = np.random.randn(n_samples, n_features)
NuSVRReg = NuSVR(kernel = 'linear', gamma = 'auto',C = 1.0, nu = 0.1)^M
NuSVRReg.fit(X, y)

Wynik

NuSVR(C = 1.0, cache_size = 200, coef0 = 0.0, degree = 3, gamma = 'auto',
   kernel = 'linear', max_iter = -1, nu = 0.1, shrinking = True, tol = 0.001,
   verbose = False)

Przykład

Teraz, po dopasowaniu, możemy uzyskać wektor wagi za pomocą następującego skryptu w Pythonie -

NuSVRReg.coef_

Wynik

array(
   [
      [-0.14904483, 0.04596145, 0.22605216, -0.08125403, 0.06564533,
      0.01104285, 0.04068767, 0.2918337 , -0.13473211, 0.36006765,
      -0.2185713 , -0.31836476, -0.03048429, 0.16102126, -0.29317051]
   ]
)

Podobnie możemy również uzyskać wartość innych atrybutów.

Liniowy SVR

Jest to liniowa regresja wektora wsparcia. Jest podobny do SVR, w którym jądro = 'linear'. Różnica między nimi polega na tymLinearSVR realizowane w zakresie liblinear, podczas gdy SVC zaimplementowano w libsvm. To jest powódLinearSVRma większą elastyczność w wyborze kar i funkcji strat. Skaluje się również lepiej do dużej liczby próbek.

Obsługuje jednak następujące parametry „strat” -

loss - ciąg, opcjonalny, domyślny = 'epsilon_insensitive'

Reprezentuje funkcję straty, gdzie strata epsilon_insensitive to strata L1, a kwadratowa strata niewrażliwa na epsilon to strata L2.

Przykład implementacji

Następujące użycie skryptu Pythona sklearn.svm.LinearSVR klasa -

from sklearn.svm import LinearSVR
from sklearn.datasets import make_regression
X, y = make_regression(n_features = 4, random_state = 0)
LSVRReg = LinearSVR(dual = False, random_state = 0,
loss = 'squared_epsilon_insensitive',tol = 1e-5)
LSVRReg.fit(X, y)

Wynik

LinearSVR(
   C=1.0, dual=False, epsilon=0.0, fit_intercept=True,
   intercept_scaling=1.0, loss='squared_epsilon_insensitive',
   max_iter=1000, random_state=0, tol=1e-05, verbose=0
)

Przykład

Teraz, po dopasowaniu, model może przewidywać nowe wartości w następujący sposób -

LSRReg.predict([[0,0,0,0]])

Wynik

array([-0.01041416])

Przykład

W powyższym przykładzie możemy uzyskać wektor wagi za pomocą następującego skryptu w Pythonie -

LSRReg.coef_

Wynik

array([20.47354746, 34.08619401, 67.23189022, 87.47017787])

Przykład

Podobnie możemy uzyskać wartość przechwycenia za pomocą następującego skryptu w Pythonie -

LSRReg.intercept_

Wynik

array([-0.01041416])