Teoria da Antena - Vetor Poynting
As antenas irradiam energia eletromagnética para transmitir ou receber informações. Portanto, os termosEnergy e Powerestão associadas a essas ondas eletromagnéticas e temos que discuti-las. Uma onda eletromagnética possui campos elétricos e magnéticos.
Considere a onda em qualquer instante, que pode ser visualizada em ambos os vetores. A figura a seguir mostra a representação dos componentes do campo elétrico e magnético em uma onda eletromagnética.
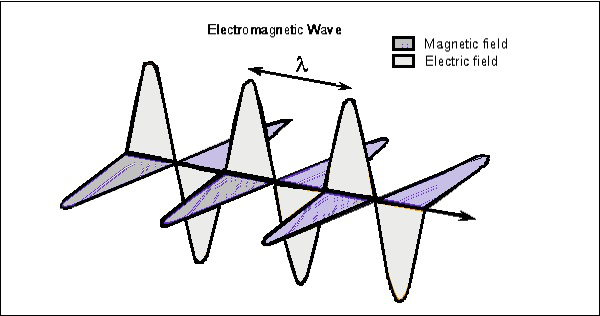
A onda elétrica está presente verticalmente à propagação da onda EM, enquanto a onda magnética está localizada horizontalmente. Ambos os campos estão em ângulos retos um com o outro.
Poynting Vector
O vetor de Poynting descreve a energia da Onda EM por unidade de tempo por unidade de área em qualquer dado instante de tempo. John Henry Poynting derivou esse vetor pela primeira vez em 1884 e, portanto, foi nomeado em sua homenagem.
Definition - “O vetor de Poynting fornece a taxa de transferência de energia por unidade de área”
ou
“A energia que uma onda carrega por unidade de tempo por unidade de área é dada pelo vetor de Poynting.”
O vetor de Poynting é representado por Ŝ.
Unidades
A unidade SI do vetor de Poynting é W/m2.
Expressão Matemática
A quantidade que é usada para descrever a potência associada às ondas eletromagnéticas é a instantânea Poynting vector, que é definido como
$$ \ hat {S} = \ hat {E} \ times \ hat {H} $$Onde
$ \ hat {S} $ é o vetor instantâneo de Poynting (W/m2).
$ \ hat {E} $ é a intensidade do campo elétrico instantâneo (V/m).
$ \ hat {H} $ é a intensidade do campo magnético instantâneo (A/m).
O ponto importante a ser observado aqui é que a magnitude de E é maior do que H dentro de uma onda EM. No entanto, ambos contribuem com a mesma quantidade de energia. Ŝ é o vetor, que tem direção e magnitude. A direção de Ŝ é igual à velocidade da onda. Sua magnitude depende de E e H.
Derivação do vetor de Poynting
Para se ter uma ideia clara do vetor de Poynting, vamos percorrer a derivação desse vetor de Poynting, em um processo passo a passo.
Vamos imaginar que uma onda EM passa uma área (A) perpendicular ao eixo X ao longo da qual a onda viaja. Ao passar por A, em tempo infinitesimal (dt), a onda percorre uma distância (dx).
$$ dx = C \ dt $$Onde
$$ C = velocidade \ de \ luz = 3 \ vezes 10 ^ {8} m / s $$ $$ volume, dv = Adx = AC \ dt $$ $$ d \ mu = \ mu \ dv = (\ epsilon_ {0} E ^ {2}) (AC \ dt) $$ $$ = \ epsilon_ {0} AC \ E ^ {2} \ dt $$Portanto, a energia transferida no tempo (dt) por área (A) é -
$$ S = \ frac {Energia} {Tempo \ vezes Área} = \ frac {dW} {dt \ A} = \ frac {\ epsilon_ {0} ACE ^ {2} \ dt} {dt \ A} = \ epsilon_ {0} C \: E ^ {2} $$Desde a
$$ \ frac {E} {H} = \ sqrt {\ frac {\ mu_ {0}} {\ epsilon_ {0}}} \ então \ S = \ frac {CB ^ {2}} {\ mu_ {0 }} $$Desde a
$$ C = \ frac {E} {H} \ then \ S = \ frac {EB} {\ mu_ {0}} $$ $$ = \ hat {S} = \ frac {1} {\ mu_ {0 }} (\ hat {E} \ hat {H}) $$Ŝ denota o vetor de Poynting.
A equação acima nos dá a energia por unidade de tempo, por unidade de área em qualquer dado instante de tempo, que é chamada de Poynting vector.