Conexões de circuito em capacitores
Em um circuito, um capacitor pode ser conectado em série ou em paralelo. Se um conjunto de capacitores fosse conectado em um circuito, o tipo de conexão do capacitor lida com os valores de tensão e corrente nessa rede.
Capacitores em série
Vamos observar o que acontece, quando poucos Capacitores estão conectados em Série. Vamos considerar três capacitores com valores diferentes, conforme mostrado na figura abaixo.

Capacitância
Quando a capacitância de uma rede cujos capacitores estão em série é considerada, o recíproco das capacitâncias de todos os capacitores, é adicionado para obter o recíproco da capacitância total. Para obter isso mais claramente,
$$ \ frac {1} {C_ {T}} \: \: = \: \: \ frac {1} {C_ {1}} \: \: + \: \: \ frac {1} {C_ { 2}} \: \: + \: \: \ frac {1} {C_ {3}} $$
Seguindo a mesma fórmula, se simplesmente dois capacitores forem conectados em série, então
$$ C_ {T} \: \: = \: \: \ frac {C_ {1} \: \: \ times \: \: C_ {2}} {C_ {1} \: \: + \: \ : C_ {2}} $$
Onde C 1 é a capacitância através do 1º capacitor, C 2 é a capacitância através do 2º capacitor e C 3 é a capacitância através do 3º capacitor na rede acima.
Voltagem
A tensão em cada capacitor depende do valor das capacitâncias individuais. Que significa
$$ V_ {C1} \: \: = \: \: \ frac {Q_ {T}} {C_ {1}} \: \: V_ {C2} \: \: = \: \: \ frac {Q_ {T}} {C_ {2}} \: \: V_ {C3} \: \: = \: \: \ frac {Q_ {T}} {C_ {3}} $$
A tensão total no circuito dos capacitores em série,
$$ V_ {T} \: \: = \: \: V_ {C1} \: \: + \: \: V_ {C2} \: \: + \: \: V_ {C3} $$
Onde V c1 é a tensão através do um r condensador, V c2 é a tensão através do 2 nd condensador e V C3 é a tensão através do 3 rd condensador na rede acima.
Atual
A quantidade total de corrente que flui através de um conjunto de capacitores conectados em série é a mesma em todos os pontos. Portanto, os capacitores armazenarão a mesma quantidade de carga, independentemente de seu valor de capacitância.
Atual através da rede,
$$ I \: \: = \: \: I_ {1} \: \: = \: \: I_ {2} \: \: = \: \: I_ {3} $$
Onde I 1 é a corrente no 1º capacitor, I 2 é a corrente no 2º capacitor e I 3 é a corrente no 3º capacitor na rede acima.
Como a corrente é a mesma, o armazenamento de carga é o mesmo porque qualquer placa de um capacitor recebe sua carga do capacitor adjacente e, portanto, os capacitores em série terão a mesma carga.
$$ Q_ {T} \: \: = \: \: Q_ {1} \: \: = \: \: Q_ {2} \: \: = \: \: Q_ {3} $$
Capacitores em paralelo
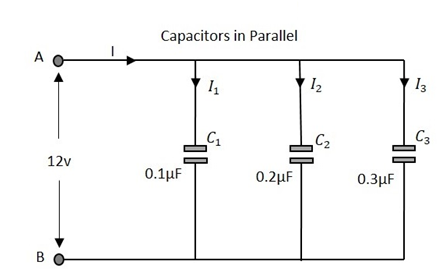
Vamos observar o que acontece, quando poucos capacitores são conectados em paralelo. Vamos considerar três capacitores com valores diferentes, conforme mostrado na figura abaixo.
Capacitância
A capacitância total do circuito é o equivalente à soma das capacitâncias individuais dos capacitores da rede.
$$ C_ {T} \: \: = \: \: C_ {1} \: \: + \: \: C_ {2} \: \: + \: \: C_ {3} $$
Onde C 1 é a capacitância através do 1º capacitor, C 2 é a capacitância através do 2º capacitor e C 3 é a capacitância através do 3º capacitor na rede acima.
Voltagem
A tensão medida no final do circuito é same como a tensão em todos os capacitores conectados em um circuito paralelo.
$$ V_ {T} \: \: = \: \: V_ {1} \: \: = \: \: V_ {2} \: \: = \: \: V_ {3} $$
Onde V c1 é a tensão através do um r condensador, V c2 é a tensão através do 2 nd condensador e V C3 é a tensão através do 3 rd condensador na rede acima.
Atual
A corrente total fluindo é igual à soma das correntes fluindo através de cada capacitor conectado na rede paralela.
$$ I_ {T} \: \: = \: \: I_ {1} \: \: + \: \: I_ {2} \: \: + \: \: I_ {3} $$
Onde I 1 é a corrente no 1º capacitor, I 2 é a corrente no 2º capacitor e I 3 é a corrente no 3º capacitor na rede acima.