Algoritmo de gráfico

Um gráfico é uma notação abstrata usada para representar a conexão entre pares de objetos. Um gráfico consiste em -

Vertices- Objetos interconectados em um gráfico são chamados de vértices. Vértices também são conhecidos comonodes.
Edges - Bordas são os links que conectam os vértices.

Existem dois tipos de gráficos -

Directed graph - Em um grafo direcionado, as arestas têm direção, ou seja, as arestas vão de um vértice a outro.
Undirected graph - Em um gráfico não direcionado, as arestas não têm direção.

Coloração de Gráfico

A coloração do gráfico é um método para atribuir cores aos vértices de um gráfico de forma que dois vértices adjacentes não tenham a mesma cor. Alguns problemas de coloração de gráfico são -

Vertex coloring - Uma forma de colorir os vértices de um gráfico de forma que não haja dois vértices adjacentes com a mesma cor.
Edge Coloring - É o método de atribuir uma cor a cada aresta de forma que duas arestas adjacentes não tenham a mesma cor.
Face coloring - Atribui uma cor a cada face ou região de um gráfico planar de modo que nenhuma das duas faces que compartilham um limite comum tenha a mesma cor.

Número Cromático

O número cromático é o número mínimo de cores necessárias para colorir um gráfico. Por exemplo, o número cromático do gráfico a seguir é 3.

O conceito de coloração de gráfico é aplicado na preparação de horários, atribuição de radiofrequência móvel, Suduku, atribuição de registro e coloração de mapas.

Etapas para colorir gráfico

Defina o valor inicial de cada processador na matriz n-dimensional como 1.
Agora, para atribuir uma cor particular a um vértice, determine se essa cor já está atribuída aos vértices adjacentes ou não.
Se um processador detectar a mesma cor nos vértices adjacentes, ele definirá seu valor na matriz como 0.
Depois de fazer n ² comparações, se qualquer elemento da matriz for 1, então é uma coloração válida.

Pseudocódigo para colorir gráfico

begin

   create the processors P(i₀,i₁,...i_n-1) where 0_i_v < m, 0 _ v < n
   status[i0,..i_n-1] = 1
	
   for j varies from 0 to n-1 do
      begin
		
         for k varies from 0 to n-1 do
         begin
            if a_j,k=1 and i_j=i_kthen
            status[i₀,..i_n-1] =0
         end
			
      end
      ok = ΣStatus
		
   if ok > 0, then display valid coloring exists
   else
      display invalid coloring
      
end

Árvore de amplitude mínima

Uma árvore geradora cuja soma de peso (ou comprimento) de todas as suas arestas é menor do que todas as outras árvores geradoras possíveis do grafo G é conhecida como um minimal spanning tree ou minimum cost spanningárvore. A figura a seguir mostra um gráfico conectado ponderado.

Algumas árvores abrangentes possíveis do gráfico acima são mostradas abaixo -

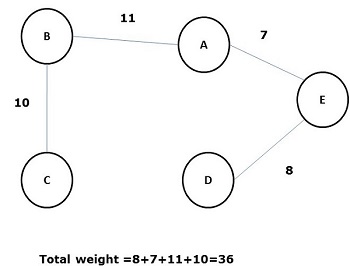
Entre todas as árvores de abrangência acima, a figura (d) é a árvore de abrangência mínima. O conceito de árvore geradora de custo mínimo é aplicado no problema do caixeiro-viajante, projetando circuitos eletrônicos, projetando redes eficientes e projetando algoritmos de roteamento eficientes.

Para implementar a árvore de abrangência de custo mínimo, os dois métodos a seguir são usados -

Algoritmo de Prim
Algoritmo de Kruskal

Algoritmo de Prim

O algoritmo de Prim é um algoritmo ganancioso, que nos ajuda a encontrar a árvore de abrangência mínima para um gráfico não direcionado ponderado. Ele seleciona um vértice primeiro e encontra uma aresta com o menor peso incidente naquele vértice.

Etapas do Algoritmo de Prim

Selecione qualquer vértice, digamos v ₁ do Gráfico G.
Selecione uma aresta, digamos e ₁ de G tal que e ₁ = v ₁ v ₂ ev ₁ ≠ v ₂ e e ₁ tenha peso mínimo entre as arestas incidentes em v ₁ no gráfico G.
Agora, seguindo a etapa 2, selecione o incidente mínimo de aresta ponderada em v ₂ .
Continue até que n – 1 arestas tenham sido escolhidas. Aquin é o número de vértices.

A árvore de abrangência mínima é -

Algoritmo de Kruskal

O algoritmo de Kruskal é um algoritmo guloso, que nos ajuda a encontrar a árvore geradora mínima para um grafo ponderado conectado, adicionando arcos de custo crescentes a cada etapa. É um algoritmo de árvore de abrangência mínima que encontra uma aresta com o menor peso possível que conecta quaisquer duas árvores na floresta.

Etapas do Algoritmo de Kruskal

Selecione uma aresta de peso mínimo; digamos que e ₁ do gráfico G e e ₁ não seja um loop.
Selecione a próxima aresta de peso mínimo conectada a e ₁ .
Continue até que n – 1 arestas tenham sido escolhidas. Aquin é o número de vértices.

A árvore de abrangência mínima do gráfico acima é -

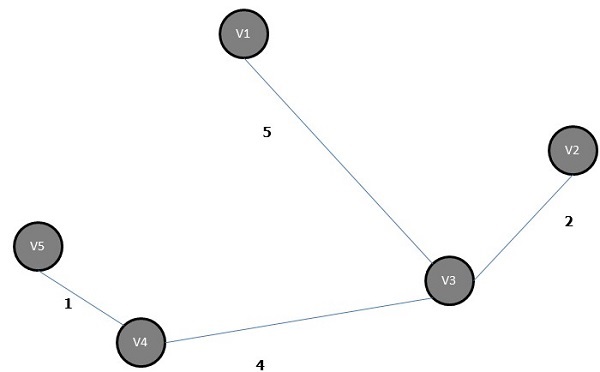
Algoritmo de caminho mais curto

O algoritmo de caminho mais curto é um método para encontrar o caminho de menor custo do nó de origem (S) ao nó de destino (D). Aqui, discutiremos o algoritmo de Moore, também conhecido como algoritmo de primeira pesquisa de amplitude.

Algoritmo de Moore

Rotule o vértice de origem, S e rotule-o i E definir i=0.
Encontre todos os vértices não rotulados adjacentes ao vértice rotulado i. Se nenhum vértice estiver conectado ao vértice S, então o vértice D não está conectado a S. Se houver vértices conectados a S, rotule-osi+1.
Se D estiver rotulado, vá para a etapa 4, caso contrário, vá para a etapa 2 para aumentar i = i + 1.
Pare depois que o comprimento do caminho mais curto for encontrado.