Física - lentes esféricas

Introdução

Um material transparente (normalmente vidro) ligado por duas superfícies, das quais uma ou ambas as superfícies são esféricas, é conhecido como "lente esférica".

Uma lente pode ter duas superfícies esféricas, salientes para fora (como mostrado na imagem abaixo), é conhecida como lente convexa ou lente convexa dupla.

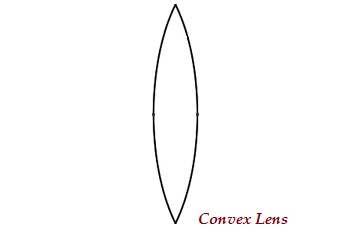
A parte do meio desta lente é abaulada (mais espessa) e nas duas extremidades é estreita.
Lentes convexas convergem os raios de luz; portanto, também é conhecido comoconverging lens.

Uma lente pode ter duas superfícies esféricas, curvadas para dentro (como mostrado na imagem abaixo), é conhecida como lente côncava ou lente côncava dupla.

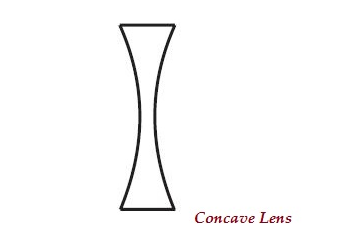
A parte do meio desta lente é estreita (curvada para dentro) e ambas as bordas são mais grossas.
Lentes côncavas divergem dos raios de luz; portanto, também é conhecido comodiverging lens.
Uma lente, côncava ou convexa, tem duas superfícies esféricas e cada uma dessas superfícies faz parte da esfera. Os centros dessas esferas são conhecidos comocenters of curvature, representado por carta em inglês 'C. '
Como existem dois centros de curvatura, portanto, representados como 'C ₁ ' e 'C _2. '
Uma linha reta imaginária, passando por ambos os centros de curvatura de uma lente, é conhecida como principal axis.
O centro óptico é o ponto central de uma lente. É representado por 'O. '
Uma abertura é o diâmetro real do contorno circular de uma lente esférica.
O foco principal da lente é representado por 'F. '
Uma lente geralmente tem dois focos representados como F ₁ e F ₂ .
Focal lengthé a distância entre o foco principal e o centro óptico de uma lente. É representado por 'f. '
A tabela a seguir ilustra a natureza e a posição das imagens formadas por uma lente convexa -

Posição do objeto	Posição da imagem	Tamanho da imagem	Natureza da Imagem
No infinito	No foco F ₂	Altamente diminuído, pontudo	Real e invertido
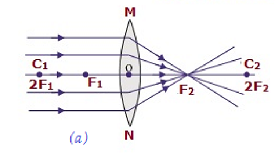
Além de 2F ₁	B / w F ₂ e 2F ₂	Diminuída	Real e invertido
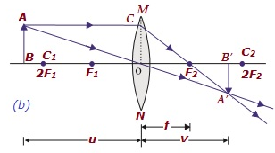
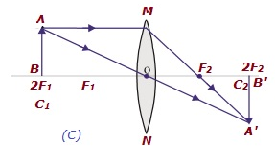
Em 2F ₁	Em 2F ₂	Mesmo tamanho	Real e invertido
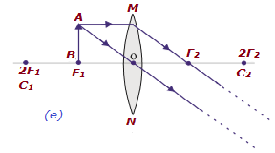
P / B F ₁ e 2F ₁	Além de 2F ₂	Ampliado	Real e invertido
Em foco F ₁	No infinito	Infinitamente grande ou muito ampliado	Real e invertido
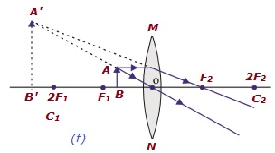
Foco P / B F ₁ e centro ótico O	No mesmo lado da lente que o objeto	Ampliado	Virtual e ereto

A tabela a seguir ilustra a natureza e a posição das imagens formadas por uma lente côncava -

Posição do objeto	Posição da imagem	Tamanho Relativo da Imagem	Natureza da Imagem	Imagem
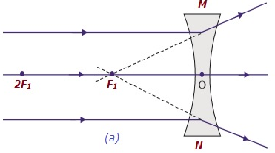
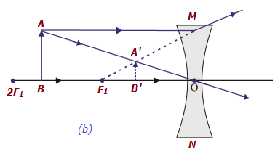
No infinito	No foco F ₁	Altamente diminuído, pontiagudo	Virtual e ereto
P / B infinito e centro ótico O da lente	P / B F ₁ e centro óptico O	Diminuir	Virtual e ereto

$$ \ frac {1} {v} - \ frac {1} {u} = \ frac {1} {f} $$

A fórmula da lente expressa as relações entre a distância do objeto (ou seja u), distância da imagem (ou seja v) e distância focal (ou seja, f) de uma lente.