Traçar números racionais em uma linha numérica

Definição

Um número racional é uma fração e é plotado em uma reta numérica da seguinte maneira.

Basic rules of representing rational no. on number line

Se o nº racional (fração) for adequado, ele estará entre 0 e 1.
Se o nº racional (fração) for impróprio, primeiro o convertemos em fração mista e, em seguida, o nº racional dado. encontra-se entre o número inteiro e o próximo número inteiro.

Usamos os seguintes passos para representar um número racional ou fração, por exemplo, $ \ frac {5} {7} $ na reta numérica.

Step 1 - Nós desenhamos uma reta numérica.

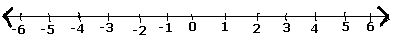
Step 2- Como o número $ \ frac {5} {7} $ é um número positivo, ele fica do lado direito do zero.

Step 3- Então, após a marca zero, temos $ \ frac {1} {7}, \: \ frac {2} {7}, \: \ frac {3} {7}, \: \ frac {4} {7 }, \: \ frac {5} {7}, \: \ frac {6} {7}, $ e ( $ \ frac {7} {7} $ = 1).

Step 4- O número racional $ \ frac {5} {7} $ na reta numérica é mostrado a seguir.

Exemplo 1:

Plote $ \ frac {1} {4} $ e $ 1 \ frac {2} {4} $ na linha numérica abaixo

Solução

Step 1:

$ \ frac {1} {4} $ (A) está entre 0 e 1; $ 1 \ frac {2} {4} $ (B) está entre 1 e 2

Step 2:

Cada divisão é dividida em quatro partes, já que a parte inferior das frações é 4.

$ \ frac {1} {4} $ é a primeira marca após 0, portanto o ponto A representa $ \ frac {1} {4} $

$ 1 \ frac {2} {4} $ é a segunda marca após 1, então o ponto B representa $ 1 \ frac {2} {4} $

Exemplo 2:

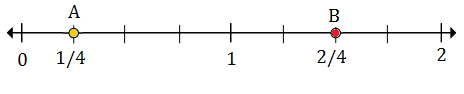
Plote $ \ frac {5} {8} $ e $ 2 \ frac {3} {8} $ na linha numérica abaixo

Solução

Step 1:

$ \ frac {5} {8} $ 8 (A) está entre 0 e 1; $ 2 \ frac {3} {8} $ (B) está entre 2 e 3

Step 2:

Cada divisão é dividida em oito partes, já que a parte inferior das frações é 8.

$ \ frac {5} {8} $ é a quinta marca após 0, portanto o ponto A representa $ \ frac {5} {8} $

$ 2 \ frac {3} {8} $ é a terceira marca após 2, então o ponto B representa $ 2 \ frac {3} {8} $