Princípios de comunicações via satélite
UMA satellite é um corpo que se move em torno de outro corpo em um caminho matematicamente previsível chamado de Orbit. Um satélite de comunicação nada mais é do que uma estação repetidora de microondas no espaço que é útil em telecomunicações, rádio e televisão, juntamente com aplicativos de Internet.
UMA repeateré um circuito que aumenta a força do sinal que recebe e o retransmite. Mas aqui este repetidor funciona como umtransponder, que muda a faixa de freqüência do sinal transmitido, a partir do recebido.
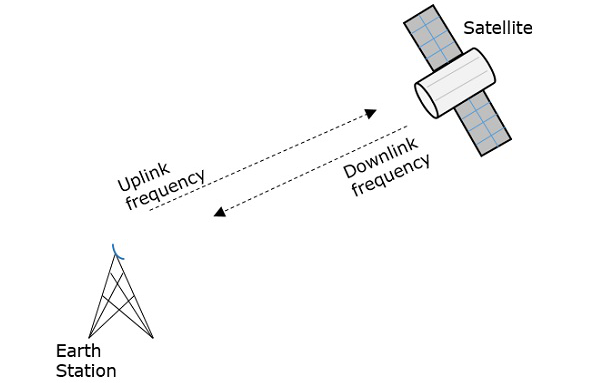
A frequência com que o sinal é enviado para o espaço é chamada Uplink frequency, enquanto a frequência com que é enviada pelo transponder é Downlink frequency.
A figura a seguir ilustra esse conceito claramente.
Agora, vamos dar uma olhada nas vantagens, desvantagens e aplicações das comunicações por satélite.
Comunicação por satélite - vantagens
Existem muitas vantagens nas comunicações por satélite, como -
Flexibility
Facilidade na instalação de novos circuitos
As distâncias são facilmente percorridas e o custo não importa
Possibilidades de transmissão
Cada canto da terra está coberto
O usuário pode controlar a rede
Comunicação via satélite - Desvantagens
A comunicação por satélite tem as seguintes desvantagens -
Os custos iniciais, como custos de segmento e lançamento, são muito altos.
Congestionamento de frequências
Interferência e propagação
Comunicação por satélite - Aplicações
A comunicação por satélite encontra suas aplicações nas seguintes áreas -
Em radiodifusão.
Em transmissão de TV, como DTH.
Em aplicativos da Internet, como fornecimento de conexão à Internet para transferência de dados, aplicativos GPS, navegação na Internet, etc.
Para comunicações de voz.
Para o setor de pesquisa e desenvolvimento, em diversas áreas.
Em aplicações e navegações militares.
A orientação do satélite em sua órbita depende das três leis chamadas de leis de Kepler.
Leis de Kepler
Johannes Kepler (1571-1630), o cientista astronômico, deu 3 leis revolucionárias a respeito do movimento dos satélites. O caminho seguido por um satélite em torno de seu principal (a Terra) é umellipse. A elipse tem dois focos -F1 e F2, a terra sendo um deles.
Se a distância do centro do objeto a um ponto em seu caminho elíptico for considerada, o ponto mais distante de uma elipse do centro é chamado de apogee e o ponto mais curto de uma elipse do centro é chamado de perigee.
Kepler 1 st Lei
1 de Kepler st lei estabelece que, “a cada gira planeta em torno do Sol em uma órbita elíptica, com o sol como um de seus focos”. Dessa forma, um satélite se move em um caminho elíptico com a Terra como um de seus focos.
O semi-eixo maior da elipse é denotado como 'a'e semi-eixo menor é denotado como b. Portanto, a excentricidade e deste sistema pode ser escrita como -
$$ e = \ frac {\ sqrt {a ^ {2} -b ^ {2}}} {a} $$
Eccentricity (e) - É o parâmetro que define a diferença na forma da elipse em vez de um círculo.
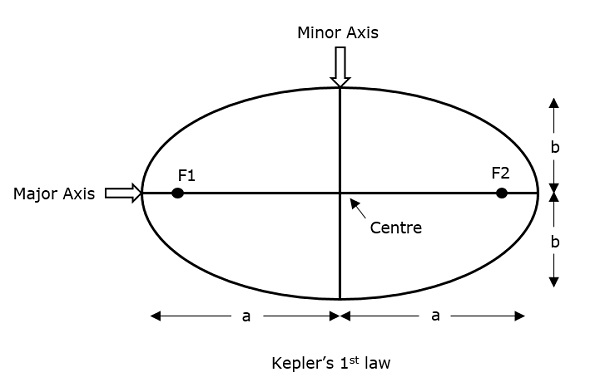
Semi-major axis (a) - É o maior diâmetro desenhado unindo os dois focos ao longo do centro, que toca ambos os apogeu (pontos mais distantes de uma elipse do centro).
Semi-minor axis (b) - É o menor diâmetro traçado pelo centro que toca ambos os perígeos (pontos mais curtos de uma elipse a partir do centro).
Eles estão bem descritos na figura a seguir.
Para um caminho elíptico, é sempre desejável que a excentricidade esteja entre 0 e 1, ou seja, 0 <e <1 porque se e torna-se zero, o caminho não terá mais a forma elíptica, mas será convertido em um caminho circular.
2ª Lei de Kepler
A 2ª lei de Kepler afirma que, “Para intervalos iguais de tempo, a área coberta pelo satélite é igual em relação ao centro da Terra”.
Isso pode ser entendido observando a figura a seguir.
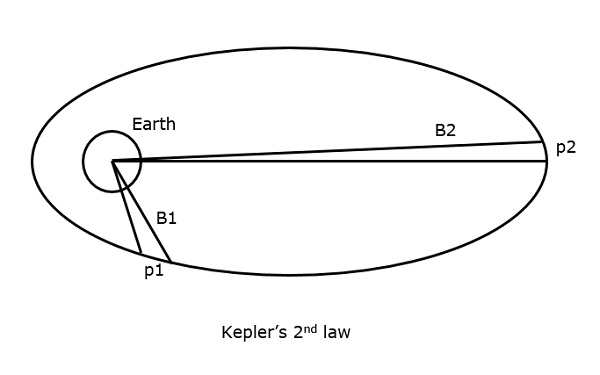
Suponha que o satélite cubra p1 e p2 distâncias, no mesmo intervalo de tempo, então as áreas B1 e B2 abrangidos em ambos os casos, respectivamente, são iguais.
3ª Lei de Kepler
A 3ª lei de Kepler afirma que “O quadrado do tempo periódico da órbita é proporcional ao cubo da distância média entre os dois corpos.”
Isso pode ser escrito matematicamente como
$$ T ^ {2} \: \ alpha \: \: a ^ {3} $$
Que implica
$$ T ^ {2} = \ frac {4 \ pi ^ {2}} {GM} a ^ {3} $$
Onde $ \ frac {4 \ pi ^ {2}} {GM} $ é a constante de proporcionalidade (de acordo com a Mecânica Newtoniana)
$$ T ^ {2} = \ frac {4 \ pi ^ {2}} {\ mu} a ^ {3} $$
Onde μ = constante gravitacional geocêntrica da Terra, ou seja, Μ = 3,986005 × 10 14 m 3 / s 2
$$ 1 = \ left (\ frac {2 \ pi} {T} \ right) ^ {2} \ frac {a ^ {3}} {\ mu} $$
$$ 1 = n ^ {2} \ frac {a ^ {3}} {\ mu} \: \: \: \ Rightarrow \: \: \: a ^ {3} = \ frac {\ mu} {n ^ {2}} $$
Onde n = o movimento médio do satélite em radianos por segundo
O funcionamento orbital dos satélites é calculado com a ajuda dessas leis de Kepler.
Junto com isso, há uma coisa importante que deve ser observada. Um satélite, quando gira em torno da Terra, sofre uma força de tração da Terra, que é a força gravitacional. Além disso, ele experimenta alguma força de atração do sol e da lua. Conseqüentemente, existem duas forças agindo sobre ele. Eles são -
Centripetal force - A força que tende a desenhar um objeto em movimento em uma trajetória, em direção a si mesmo é chamada de centripetal force.
Centrifugal force - A força que tende a empurrar um objeto em movimento em uma trajetória, para longe de sua posição, é chamada de centrifugal force.
Portanto, um satélite deve equilibrar essas duas forças para se manter em sua órbita.
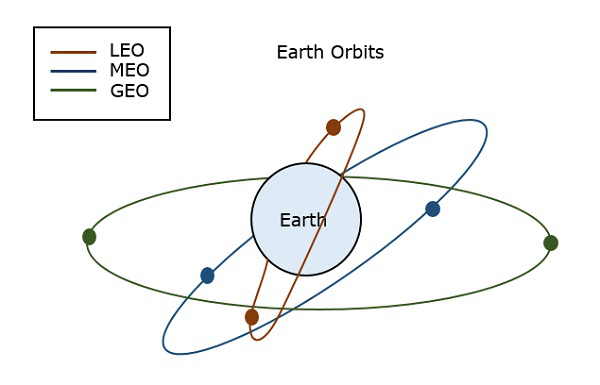
Órbitas terrestres
Um satélite, quando lançado ao espaço, precisa ser colocado em uma determinada órbita para fornecer um caminho particular para sua revolução, de modo a manter a acessibilidade e servir ao seu propósito seja científico, militar ou comercial. Essas órbitas que são atribuídas a satélites, em relação à terra, são chamadas deEarth Orbits. Os satélites nessas órbitas são da TerraOrbit Satellites.
Os tipos importantes de órbitas terrestres são -
Órbita terrestre geo-síncrona
Órbita Terrestre Média
Órbita terrestre baixa
Satélites de órbita terrestre geossíncrona
UMA Geo-Synchronous Earth Orbit (GEO)satélite é aquele que é colocado a uma altitude de 22.300 milhas acima da Terra. Esta órbita é sincronizada com umside real day(ou seja, 23 horas e 56 minutos). Esta órbita podehave inclination and eccentricity. Pode não ser circular. Esta órbita pode ser inclinada nos pólos da Terra. Mas parece estacionário quando observado da Terra.
A mesma órbita geo-síncrona, se for circular e no plano do equador, é chamada de geo-stationary orbit. Esses satélites são colocados a 35.900kms (o mesmo que geossíncrono) acima do Equador da Terra e continuam girando em relação à direção da Terra (oeste para leste). Esses satélites são considerados estacionários em relação à Terra e, portanto, o nome indica.
Os satélites de órbita terrestre geo-estacionária são usados para previsão do tempo, TV por satélite, rádio por satélite e outros tipos de comunicações globais.
A figura a seguir mostra a diferença entre as órbitas geo-síncronas e geoestacionárias. O eixo de rotação indica o movimento da Terra.
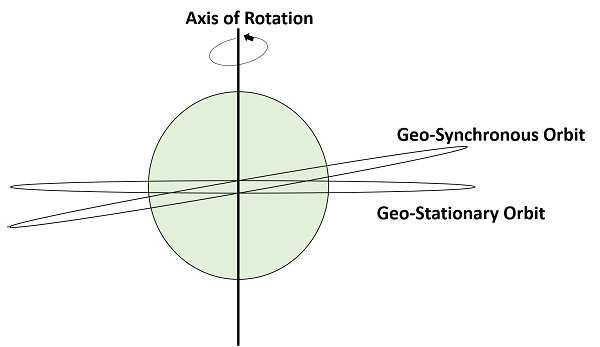
Note- Cada órbita geo-estacionária é uma órbita geo-síncrona. Mas toda órbita geo-síncrona NÃO é uma órbita geoestacionária.
Satélites de órbita terrestre média
Medium Earth Orbit (MEO)as redes de satélites orbitarão a distâncias de cerca de 8.000 milhas da superfície da Terra. Os sinais transmitidos por um satélite MEO percorrem uma distância mais curta. Isso se traduz em maior intensidade do sinal na extremidade receptora. Isso mostra que terminais de recepção menores e mais leves podem ser usados na extremidade de recepção.
Como o sinal está viajando por uma distância menor de e para o satélite, há menos atraso na transmissão. Transmission delay pode ser definido como o tempo que leva para um sinal viajar até um satélite e voltar para uma estação receptora.
Para comunicações em tempo real, quanto menor o atraso de transmissão, melhor será o sistema de comunicação. Por exemplo, se um satélite GEO requer 0,25 segundos para uma viagem de ida e volta, o satélite MEO requer menos de 0,1 segundos para completar a mesma viagem. MEOs opera na faixa de frequência de 2 GHz e acima.
Satélites de baixa órbita terrestre
Os satélites de Low Earth Orbit (LEO) são classificados principalmente em três categorias, a saber, pequenos LEOs, grandes LEOs e Mega-LEOs. LEOs orbitarão a uma distância de 500 a 1000 milhas acima da superfície da Terra.
Essa distância relativamente curta reduz o atraso de transmissão para apenas 0,05 segundos. Isso reduz ainda mais a necessidade de equipamentos de recepção sensíveis e volumosos. Os pequenos LEOs operarão na faixa de 800 MHz (0,8 GHz). Os Big LEOs operam na faixa de 2 GHz ou acima, e os Mega-LEOs operam na faixa de 20-30 GHz.
As frequências mais altas associadas a Mega-LEOs se traduz em mais capacidade de transporte de informações e rende a capacidade de esquema de transmissão de vídeo em tempo real com baixo atraso.
A figura a seguir mostra os caminhos de LEO, MEO e GEO.