SciPy - ODR
ODR significa Orthogonal Distance Regression, que é usado nos estudos de regressão. A regressão linear básica é freqüentemente usada para estimar a relação entre as duas variáveisy e x desenhando a linha de melhor ajuste no gráfico.
O método matemático usado para isso é conhecido como Least Squares, e visa minimizar a soma do erro quadrático para cada ponto. A questão chave aqui é como você calcula o erro (também conhecido como residual) para cada ponto.
Em uma regressão linear padrão, o objetivo é prever o valor de Y a partir do valor de X - portanto, a coisa sensata a fazer é calcular o erro nos valores de Y (mostrado como as linhas cinzas na imagem a seguir). No entanto, às vezes é mais sensato levar em consideração o erro em X e Y (conforme mostrado pelas linhas vermelhas pontilhadas na imagem a seguir).
Por exemplo - quando você sabe que suas medições de X são incertas, ou quando você não quer se concentrar nos erros de uma variável em relação a outra.
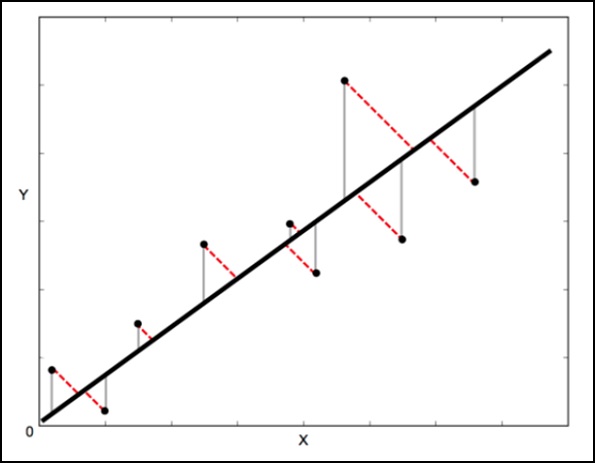
A regressão de distância ortogonal (ODR) é um método que pode fazer isso (ortogonal neste contexto significa perpendicular - portanto, ele calcula erros perpendiculares à linha, em vez de apenas 'verticalmente').
Implementação scipy.odr para regressão univariada
O exemplo a seguir demonstra a implementação de scipy.odr para regressão univariada.
import numpy as np
import matplotlib.pyplot as plt
from scipy.odr import *
import random
# Initiate some data, giving some randomness using random.random().
x = np.array([0, 1, 2, 3, 4, 5])
y = np.array([i**2 + random.random() for i in x])
# Define a function (quadratic in our case) to fit the data with.
def linear_func(p, x):
m, c = p
return m*x + c
# Create a model for fitting.
linear_model = Model(linear_func)
# Create a RealData object using our initiated data from above.
data = RealData(x, y)
# Set up ODR with the model and data.
odr = ODR(data, linear_model, beta0=[0., 1.])
# Run the regression.
out = odr.run()
# Use the in-built pprint method to give us results.
out.pprint()O programa acima irá gerar a seguinte saída.
Beta: [ 5.51846098 -4.25744878]
Beta Std Error: [ 0.7786442 2.33126407]
Beta Covariance: [
[ 1.93150969 -4.82877433]
[ -4.82877433 17.31417201
]]
Residual Variance: 0.313892697582
Inverse Condition #: 0.146618499389
Reason(s) for Halting:
Sum of squares convergence