Série Temporal - Guia Rápido
Uma série temporal é uma sequência de observações durante um determinado período. Uma série de tempo univariada consiste nos valores tomados por uma única variável em instâncias de tempo periódicas ao longo de um período, e uma série de tempo multivariada consiste nos valores tomados por várias variáveis nas mesmas instâncias de tempo periódicas ao longo de um período. O exemplo mais simples de uma série temporal que todos nós encontramos no dia a dia é a mudança na temperatura ao longo do dia, semana, mês ou ano.
A análise de dados temporais é capaz de nos dar insights úteis sobre como uma variável muda ao longo do tempo, ou como ela depende da mudança nos valores de outra (s) variável (s). Esta relação de uma variável com seus valores anteriores e / ou outras variáveis pode ser analisada para previsão de séries temporais e tem inúmeras aplicações em inteligência artificial.
Um conhecimento básico de qualquer linguagem de programação é essencial para que um usuário trabalhe ou desenvolva problemas de aprendizado de máquina. Uma lista de linguagens de programação preferidas para quem deseja trabalhar com aprendizado de máquina é fornecida abaixo -
Pitão
É uma linguagem de programação interpretada de alto nível, rápida e fácil de codificar. Python pode seguir paradigmas de programação procedural ou orientada a objetos. A presença de uma variedade de bibliotecas torna a implementação de procedimentos complicados mais simples. Neste tutorial, estaremos codificando em Python e as bibliotecas correspondentes úteis para modelagem de séries temporais serão discutidas nos próximos capítulos.
R
Semelhante ao Python, R é uma linguagem multiparadigma interpretada, que suporta computação estatística e gráficos. A variedade de pacotes torna mais fácil implementar a modelagem de aprendizado de máquina em R.
Java
É uma linguagem de programação orientada a objetos interpretada, que é amplamente conhecida por uma grande variedade de disponibilidade de pacotes e técnicas sofisticadas de visualização de dados.
C / C ++
Estas são linguagens compiladas e duas das linguagens de programação mais antigas. Muitas vezes, essas linguagens são preferidas para incorporar recursos de ML nos aplicativos já existentes, pois permitem personalizar facilmente a implementação de algoritmos de ML.
MATLAB
MATrix LABoratory é uma linguagem multiparadigma que dá funcionamento para trabalhar com matrizes. Ele permite operações matemáticas para problemas complexos. É usado principalmente para operações numéricas, mas alguns pacotes também permitem a simulação gráfica de múltiplos domínios e design baseado em modelo.
Outras linguagens de programação preferidas para problemas de aprendizado de máquina incluem JavaScript, LISP, Prolog, SQL, Scala, Julia, SAS etc.
Python tem uma popularidade estabelecida entre os indivíduos que realizam aprendizado de máquina por causa de sua estrutura de código fácil de escrever e entender, bem como uma ampla variedade de bibliotecas de código aberto. Algumas dessas bibliotecas de código aberto que usaremos nos próximos capítulos foram apresentadas a seguir.
NumPy
Python Numérica é uma biblioteca usada para computação científica. Ele funciona em um objeto de matriz N-dimensional e fornece funcionalidade matemática básica, como tamanho, forma, média, desvio padrão, mínimo, máximo, bem como algumas funções mais complexas, como funções algébricas lineares e transformada de Fourier. Você aprenderá mais sobre isso à medida que avançarmos neste tutorial.
Pandas
Esta biblioteca fornece estruturas de dados altamente eficientes e fáceis de usar, como séries, dataframes e painéis. Ele aprimorou a funcionalidade do Python, desde a mera coleta e preparação de dados até a análise de dados. As duas bibliotecas, Pandas e NumPy, tornam muito simples qualquer operação em conjuntos de dados pequenos a muito grandes. Para saber mais sobre essas funções, siga este tutorial.
SciPy
Science Python é uma biblioteca usada para computação científica e técnica. Oferece funcionalidades de otimização, processamento de sinais e imagens, integração, interpolação e álgebra linear. Essa biblioteca é útil durante a execução do aprendizado de máquina. Discutiremos essas funcionalidades à medida que avançamos neste tutorial.
Scikit Learn
Esta biblioteca é um kit de ferramentas SciPy amplamente utilizado para modelagem estatística, aprendizado de máquina e aprendizado profundo, pois contém vários modelos personalizáveis de regressão, classificação e agrupamento. Funciona bem com Numpy, Pandas e outras bibliotecas, o que o torna mais fácil de usar.
Statsmodels
Como o Scikit Learn, esta biblioteca é usada para exploração de dados estatísticos e modelagem estatística. Ele também funciona bem com outras bibliotecas Python.
Matplotlib
Esta biblioteca é usada para visualização de dados em vários formatos, como gráfico de linha, gráfico de barra, mapas de calor, gráficos de dispersão, histograma, etc. Ela contém todas as funcionalidades relacionadas ao gráfico necessárias desde a plotagem até a rotulagem. Discutiremos essas funcionalidades à medida que avançamos neste tutorial.
Essas bibliotecas são muito essenciais para iniciar o aprendizado de máquina com qualquer tipo de dado.
Ao lado das discutidas acima, outra biblioteca especialmente significativa para lidar com séries temporais é -
Data hora
Esta biblioteca, com seus dois módulos - datetime e calendar, fornece todas as funcionalidades datetime necessárias para ler, formatar e manipular o tempo.
Estaremos usando essas bibliotecas nos próximos capítulos.
A série temporal é uma sequência de observações indexadas em intervalos de tempo equidistantes. Portanto, a ordem e a continuidade devem ser mantidas em qualquer série temporal.
O conjunto de dados que usaremos é uma série temporal multivariada com dados horários de aproximadamente um ano, para a qualidade do ar em uma cidade italiana significativamente poluída. O conjunto de dados pode ser baixado do link fornecido abaixo -https://archive.ics.uci.edu/ml/datasets/air+quality.
É necessário ter certeza de que -
A série temporal é igualmente espaçada e
Não há valores redundantes ou lacunas nele.
Caso a série temporal não seja contínua, podemos aumentar ou diminuir a resolução.
Mostrando df.head ()
Em [122]:
import pandasEm [123]:
df = pandas.read_csv("AirQualityUCI.csv", sep = ";", decimal = ",")
df = df.iloc[ : , 0:14]Em [124]:
len(df)Fora [124]:
9471Em [125]:
df.head()Fora [125]:

Para pré-processar a série temporal, certificamo-nos de que não há valores NaN (NULL) no conjunto de dados; se houver, podemos substituí-los por 0 ou valores médios ou precedentes ou sucessivos. Substituir é uma escolha preferida em vez de descartar para que a continuidade da série temporal seja mantida. No entanto, em nosso conjunto de dados, os últimos valores parecem ser NULL e, portanto, a eliminação não afetará a continuidade.
Eliminando NaN (não é um número)
Em [126]:
df.isna().sum()
Out[126]:
Date 114
Time 114
CO(GT) 114
PT08.S1(CO) 114
NMHC(GT) 114
C6H6(GT) 114
PT08.S2(NMHC) 114
NOx(GT) 114
PT08.S3(NOx) 114
NO2(GT) 114
PT08.S4(NO2) 114
PT08.S5(O3) 114
T 114
RH 114
dtype: int64Em [127]:
df = df[df['Date'].notnull()]Em [128]:
df.isna().sum()Fora [128]:
Date 0
Time 0
CO(GT) 0
PT08.S1(CO) 0
NMHC(GT) 0
C6H6(GT) 0
PT08.S2(NMHC) 0
NOx(GT) 0
PT08.S3(NOx) 0
NO2(GT) 0
PT08.S4(NO2) 0
PT08.S5(O3) 0
T 0
RH 0
dtype: int64As séries temporais geralmente são plotadas como gráficos de linha em relação ao tempo. Para isso, vamos combinar a coluna de data e hora e convertê-la em um objeto datetime a partir de strings. Isso pode ser feito usando a biblioteca datetime.
Convertendo em objeto datetime
Em [129]:
df['DateTime'] = (df.Date) + ' ' + (df.Time)
print (type(df.DateTime[0]))<class 'str'>
Em [130]:
import datetime
df.DateTime = df.DateTime.apply(lambda x: datetime.datetime.strptime(x, '%d/%m/%Y %H.%M.%S'))
print (type(df.DateTime[0]))<classe 'pandas._libs.tslibs.timestamps.Timestamp'>
Vamos ver como algumas variáveis, como a temperatura, mudam com a mudança no tempo.
Mostrando plotagens
Em [131]:
df.index = df.DateTimeEm [132]:
import matplotlib.pyplot as plt
plt.plot(df['T'])Fora [132]:
[<matplotlib.lines.Line2D at 0x1eaad67f780>]
Em [208]:
plt.plot(df['C6H6(GT)'])Fora [208]:
[<matplotlib.lines.Line2D at 0x1eaaeedff28>]Box-plots são outro tipo de gráfico útil que permite condensar muitas informações sobre um conjunto de dados em um único gráfico. Mostra a média, quartil 25% e 75% e outliers de uma ou múltiplas variáveis. No caso em que o número de outliers é pequeno e muito distante da média, podemos eliminar os outliers configurando-os para o valor médio ou o valor do quartil de 75%.
Mostrando Boxplots
Em [134]:
plt.boxplot(df[['T','C6H6(GT)']].values)Fora [134]:
{'whiskers': [<matplotlib.lines.Line2D at 0x1eaac16de80>,
<matplotlib.lines.Line2D at 0x1eaac16d908>,
<matplotlib.lines.Line2D at 0x1eaac177a58>,
<matplotlib.lines.Line2D at 0x1eaac177cf8>],
'caps': [<matplotlib.lines.Line2D at 0x1eaac16d2b0>,
<matplotlib.lines.Line2D at 0x1eaac16d588>,
<matplotlib.lines.Line2D at 0x1eaac1a69e8>,
<matplotlib.lines.Line2D at 0x1eaac1a64a8>],
'boxes': [<matplotlib.lines.Line2D at 0x1eaac16dc50>,
<matplotlib.lines.Line2D at 0x1eaac1779b0>],
'medians': [<matplotlib.lines.Line2D at 0x1eaac16d4a8>,
<matplotlib.lines.Line2D at 0x1eaac1a6c50>],
'fliers': [<matplotlib.lines.Line2D at 0x1eaac177dd8>,
<matplotlib.lines.Line2D at 0x1eaac1a6c18>],'means': []
}
Introdução
Uma série temporal tem 4 componentes, conforme abaixo -
Level - É o valor médio em torno do qual a série varia.
Trend - É o comportamento crescente ou decrescente de uma variável com o tempo.
Seasonality - É o comportamento cíclico das séries temporais.
Noise - É o erro nas observações adicionadas devido a fatores ambientais.
Técnicas de modelagem de séries temporais
Para capturar esses componentes, existem várias técnicas populares de modelagem de séries temporais. Esta seção fornece uma breve introdução de cada técnica, no entanto, discutiremos sobre elas em detalhes nos próximos capítulos -
Métodos ingênuos
Essas são técnicas de estimativa simples, como o valor previsto recebe o valor igual à média dos valores anteriores da variável dependente do tempo ou valor real anterior. Eles são usados para comparação com técnicas de modelagem sofisticadas.
Auto Regressão
A regressão automática prevê os valores de períodos de tempo futuros como uma função dos valores de períodos de tempo anteriores. As previsões de regressão automática podem se ajustar aos dados melhor do que os métodos ingênuos, mas podem não ser capazes de contabilizar a sazonalidade.
Modelo ARIMA
Uma média móvel integrada auto-regressiva modela o valor de uma variável como uma função linear de valores anteriores e erros residuais em etapas de tempo anteriores de uma série de tempo estacionária. No entanto, os dados do mundo real podem ser não estacionários e ter sazonalidade, portanto, Sazonal-ARIMA e Fracional-ARIMA foram desenvolvidos. ARIMA funciona em séries temporais univariadas, para lidar com múltiplas variáveis VARIMA foi introduzido.
Suavização Exponencial
Ele modela o valor de uma variável como uma função linear ponderada exponencial de valores anteriores. Este modelo estatístico também pode lidar com tendências e sazonalidade.
LSTM
O modelo de memória de longo prazo (LSTM) é uma rede neural recorrente usada para séries temporais para contabilizar dependências de longo prazo. Ele pode ser treinado com grande quantidade de dados para capturar as tendências em séries temporais multivariadas.
As ditas técnicas de modelagem são usadas para regressão de séries temporais. Nos próximos capítulos, vamos explorar tudo isso um por um.
Introdução
Qualquer modelo estatístico ou de aprendizado de máquina tem alguns parâmetros que influenciam muito como os dados são modelados. Por exemplo, ARIMA possui valores p, d, q. Esses parâmetros devem ser decididos de forma que o erro entre os valores reais e os valores modelados seja mínimo. A calibração de parâmetros é considerada a tarefa mais crucial e demorada de ajuste de modelo. Portanto, é muito essencial para nós escolhermos os parâmetros ideais.
Métodos para calibração de parâmetros
Existem várias maneiras de calibrar os parâmetros. Esta seção fala sobre alguns deles em detalhes.
Hit-and-try
Uma maneira comum de calibrar modelos é a calibragem manual, onde você começa visualizando a série temporal e intuitivamente tenta alguns valores de parâmetro e os altera continuamente até obter um ajuste bom o suficiente. Requer um bom entendimento do modelo que estamos testando. Para o modelo ARIMA, a calibração manual é feita com a ajuda do gráfico de autocorrelação para o parâmetro 'p', gráfico de autocorrelação parcial para o parâmetro 'q' e teste ADF para confirmar a estacionariedade da série temporal e configuração do parâmetro 'd' . Discutiremos tudo isso em detalhes nos próximos capítulos.
Pesquisa de grade
Outra forma de calibrar modelos é por busca em grade, o que essencialmente significa que você tenta construir um modelo para todas as combinações possíveis de parâmetros e selecionar aquele com erro mínimo. Isso é demorado e, portanto, é útil quando o número de parâmetros a serem calibrados e a faixa de valores que eles assumem são menores, pois isso envolve vários loops for aninhados.
Algoritmo genético
O algoritmo genético trabalha com o princípio biológico de que uma boa solução acabará evoluindo para a solução mais 'ótima'. Ele usa operações biológicas de mutação, cruzamento e seleção para finalmente chegar a uma solução ótima.
Para obter mais conhecimento, você pode ler sobre outras técnicas de otimização de parâmetros, como otimização Bayesiana e otimização de Swarm.
Introdução
Métodos ingênuos, como assumir o valor previsto no tempo 't' como o valor real da variável no tempo 't-1' ou média móvel da série, são usados para avaliar o quão bem os modelos estatísticos e modelos de aprendizado de máquina podem executar e enfatizar sua necessidade.
Neste capítulo, vamos experimentar esses modelos em um dos recursos de nossos dados de série temporal.
Primeiro, veremos a média do recurso de 'temperatura' de nossos dados e o desvio em torno dele. Também é útil ver os valores máximos e mínimos de temperatura. Podemos usar as funcionalidades da biblioteca numpy aqui.
Mostrando estatísticas
Em [135]:
import numpy
print (
'Mean: ',numpy.mean(df['T']), ';
Standard Deviation: ',numpy.std(df['T']),';
\nMaximum Temperature: ',max(df['T']),';
Minimum Temperature: ',min(df['T'])
)Temos as estatísticas para todas as 9357 observações na linha do tempo com espaçamento igual, que são úteis para entendermos os dados.
Agora vamos tentar o primeiro método ingênuo, definindo o valor previsto no momento igual ao valor real no momento anterior e calcular a raiz do erro quadrático médio (RMSE) para quantificar o desempenho desse método.
Que mostra uma r método naïve
Em [136]:
df['T']
df['T_t-1'] = df['T'].shift(1)Em [137]:
df_naive = df[['T','T_t-1']][1:]Em [138]:
from sklearn import metrics
from math import sqrt
true = df_naive['T']
prediction = df_naive['T_t-1']
error = sqrt(metrics.mean_squared_error(true,prediction))
print ('RMSE for Naive Method 1: ', error)RMSE para Método Naive 1: 12.901140576492974
Vejamos o próximo método ingênuo, onde o valor previsto no tempo presente é igualado à média dos períodos de tempo que o precedem. Iremos calcular o RMSE para este método também.
Mostrando 2 nd método naïve
Em [139]:
df['T_rm'] = df['T'].rolling(3).mean().shift(1)
df_naive = df[['T','T_rm']].dropna()Em [140]:
true = df_naive['T']
prediction = df_naive['T_rm']
error = sqrt(metrics.mean_squared_error(true,prediction))
print ('RMSE for Naive Method 2: ', error)RMSE for Naive Method 2: 14.957633272839242
Aqui, você pode experimentar vários períodos anteriores também chamados de 'atrasos' que deseja considerar, que são mantidos como 3 aqui. Nestes dados, pode ser visto que conforme você aumenta o número de defasagens e o erro aumenta. Se o lag for mantido em 1, ele se tornará o mesmo método ingênuo usado anteriormente.
Points to Note
Você pode escrever uma função muito simples para calcular a raiz do erro quadrático médio. Aqui, usamos a função de erro quadrático médio do pacote 'sklearn' e então obtemos sua raiz quadrada.
No pandas, df ['column_name'] também pode ser escrito como df.column_name, entretanto, para esse conjunto de dados, df.T não funcionará da mesma forma que df ['T'] porque df.T é a função para transpor um dataframe. Portanto, use apenas df ['T'] ou considere renomear esta coluna antes de usar a outra sintaxe.
Para uma série temporal estacionária, um modelo de regressão automática vê o valor de uma variável no tempo 't' como uma função linear dos valores 'p' em etapas anteriores. Matematicamente, pode ser escrito como -
$$y_{t} = \:C+\:\phi_{1}y_{t-1}\:+\:\phi_{2}Y_{t-2}+...+\phi_{p}y_{t-p}+\epsilon_{t}$$
Onde, 'p' é o parâmetro de tendência auto-regressiva
$\epsilon_{t}$ é ruído branco, e
$y_{t-1}, y_{t-2}\:\: ...y_{t-p}$ denotam o valor da variável em períodos anteriores.
O valor de p pode ser calibrado usando vários métodos. Uma maneira de encontrar o valor apt de 'p' é traçar o gráfico de autocorrelação.
Note- Devemos separar os dados em treinar e testar na proporção de 8: 2 do total de dados disponíveis antes de fazer qualquer análise nos dados, porque os dados de teste servem apenas para descobrir a precisão do nosso modelo e a suposição é que não está disponível para nós até depois que as previsões foram feitas. No caso de séries temporais, a sequência de pontos de dados é muito essencial, portanto, deve-se ter em mente para não perder a ordem durante a divisão dos dados.
Um gráfico de autocorrelação ou correlograma mostra a relação de uma variável consigo mesma em etapas de tempo anteriores. Faz uso da correlação de Pearson e mostra as correlações dentro do intervalo de confiança de 95%. Vamos ver como fica a variável de 'temperatura' de nossos dados.
Mostrando ACP
Em [141]:
split = len(df) - int(0.2*len(df))
train, test = df['T'][0:split], df['T'][split:]Em [142]:
from statsmodels.graphics.tsaplots import plot_acf
plot_acf(train, lags = 100)
plt.show()
Todos os valores de latência fora da região sombreada em azul são considerados como tendo uma correlação.
Para uma série temporal estacionária, um modelo de média móvel vê o valor de uma variável no tempo 't' como uma função linear de erros residuais de 'q' etapas de tempo que a precedem. O erro residual é calculado comparando o valor no momento 't' com a média móvel dos valores anteriores.
Matematicamente, pode ser escrito como -
$$y_{t} = c\:+\:\epsilon_{t}\:+\:\theta_{1}\:\epsilon_{t-1}\:+\:\theta_{2}\:\epsilon_{t-2}\:+\:...+:\theta_{q}\:\epsilon_{t-q}\:$$
Onde 'q' é o parâmetro de tendência da média móvel
$\epsilon_{t}$ é ruído branco, e
$\epsilon_{t-1}, \epsilon_{t-2}...\epsilon_{t-q}$ são os termos de erro em períodos anteriores.
O valor de 'q' pode ser calibrado usando vários métodos. Uma maneira de encontrar o valor apt de 'q' é traçar o gráfico de autocorrelação parcial.
Um gráfico de autocorrelação parcial mostra a relação de uma variável consigo mesma em etapas de tempo anteriores com as correlações indiretas removidas, ao contrário do gráfico de autocorrelação que mostra correlações diretas e indiretas, vamos ver como fica para a variável de 'temperatura' de nosso dados.
Mostrando PACP
Em [143]:
from statsmodels.graphics.tsaplots import plot_pacf
plot_pacf(train, lags = 100)
plt.show()
Uma autocorrelação parcial é lida da mesma forma que um correlograma.
Já entendemos que, para uma série temporal estacionária, uma variável no tempo 't' é uma função linear de observações anteriores ou erros residuais. Portanto, é hora de combinarmos os dois e ter um modelo de média móvel auto-regressiva (ARMA).
No entanto, às vezes a série temporal não é estacionária, ou seja, as propriedades estatísticas de uma série como a média, a variância muda ao longo do tempo. E os modelos estatísticos que estudamos até agora assumem que as séries temporais são estacionárias, portanto, podemos incluir uma etapa de pré-processamento de diferenciar as séries temporais para torná-las estacionárias. Agora, é importante descobrirmos se a série temporal com a qual estamos lidando é estacionária ou não.
Vários métodos para encontrar a estacionariedade de uma série temporal procuram sazonalidade ou tendência no gráfico das séries temporais, verificando a diferença na média e variância para vários períodos de tempo, teste Dickey-Fuller Aumentado (ADF), teste KPSS, expoente de Hurst etc. .
Vamos ver se a variável de 'temperatura' do nosso conjunto de dados é uma série temporal estacionária ou não usando o teste ADF.
Em [74]:
from statsmodels.tsa.stattools import adfuller
result = adfuller(train)
print('ADF Statistic: %f' % result[0])
print('p-value: %f' % result[1])
print('Critical Values:')
for key, value In result[4].items()
print('\t%s: %.3f' % (key, value))Estatística ADF: -10,406056
valor p: 0,000000
Valores Críticos:
1%: -3,431
5%: -2,862
10%: -2.567
Agora que executamos o teste ADF, vamos interpretar o resultado. Primeiro, compararemos a estatística ADF com os valores críticos, um valor crítico inferior nos diz que a série é provavelmente não estacionária. A seguir, vemos o valor p. Um valor de p maior que 0,05 também sugere que a série temporal não é estacionária.
Como alternativa, o valor de p menor ou igual a 0,05 ou a estatística ADF menor que os valores críticos sugerem que a série temporal é estacionária.
Portanto, a série temporal com a qual estamos lidando já é estacionária. No caso de séries temporais estacionárias, definimos o parâmetro 'd' como 0.
Também podemos confirmar a estacionariedade das séries temporais usando o expoente de Hurst.
Em [75]:
import hurst
H, c,data = hurst.compute_Hc(train)
print("H = {:.4f}, c = {:.4f}".format(H,c))H = 0,1660, c = 5,0740
O valor de H <0,5 mostra comportamento anti-persistente, e H> 0,5 mostra comportamento persistente ou uma série de tendências. H = 0,5 mostra passeio aleatório / movimento browniano. O valor de H <0,5, confirmando que nossa série é estacionária.
Para séries temporais não estacionárias, definimos o parâmetro 'd' como 1. Além disso, o valor do parâmetro de tendência auto-regressiva 'p' e o parâmetro de tendência média móvel 'q' é calculado na série temporal estacionária, ou seja, plotando ACP e PACP após diferenciar as séries temporais.
O modelo ARIMA, que é caracterizado por 3 parâmetros, (p, d, q) está claro para nós, então vamos modelar nossa série temporal e prever os valores futuros de temperatura.
Em [156]:
from statsmodels.tsa.arima_model import ARIMA
model = ARIMA(train.values, order=(5, 0, 2))
model_fit = model.fit(disp=False)Em [157]:
predictions = model_fit.predict(len(test))
test_ = pandas.DataFrame(test)
test_['predictions'] = predictions[0:1871]Em [158]:
plt.plot(df['T'])
plt.plot(test_.predictions)
plt.show()
Em [167]:
error = sqrt(metrics.mean_squared_error(test.values,predictions[0:1871]))
print ('Test RMSE for ARIMA: ', error)Teste RMSE para ARIMA: 43.21252940234892
No capítulo anterior, vimos como o modelo ARIMA funciona e suas limitações de não poder lidar com dados sazonais ou séries temporais multivariadas e, portanto, novos modelos foram introduzidos para incluir esses recursos.
Um vislumbre desses novos modelos é dado aqui -
Auto-regressão vetorial (VAR)
É uma versão generalizada do modelo de auto regressão para séries temporais estacionárias multivariadas. É caracterizado pelo parâmetro 'p'.
Média móvel vetorial (VMA)
É uma versão generalizada do modelo de média móvel para séries temporais estacionárias multivariadas. É caracterizado pelo parâmetro 'q'.
Média móvel de regressão automática vetorial (VARMA)
É a combinação de VAR e VMA e uma versão generalizada do modelo ARMA para séries temporais estacionárias multivariadas. É caracterizado pelos parâmetros 'p' e 'q'. Muito parecido, ARMA é capaz de agir como um modelo AR definindo o parâmetro 'q' como 0 e como um modelo MA definindo o parâmetro 'p' como 0, VARMA também é capaz de agir como um modelo VAR definindo o parâmetro 'q' como 0 e como um modelo VMA definindo o parâmetro 'p' como 0.
Em [209]:
df_multi = df[['T', 'C6H6(GT)']]
split = len(df) - int(0.2*len(df))
train_multi, test_multi = df_multi[0:split], df_multi[split:]Em [211]:
from statsmodels.tsa.statespace.varmax import VARMAX
model = VARMAX(train_multi, order = (2,1))
model_fit = model.fit()
c:\users\naveksha\appdata\local\programs\python\python37\lib\site-packages\statsmodels\tsa\statespace\varmax.py:152:
EstimationWarning: Estimation of VARMA(p,q) models is not generically robust,
due especially to identification issues.
EstimationWarning)
c:\users\naveksha\appdata\local\programs\python\python37\lib\site-packages\statsmodels\tsa\base\tsa_model.py:171:
ValueWarning: No frequency information was provided, so inferred frequency H will be used.
% freq, ValueWarning)
c:\users\naveksha\appdata\local\programs\python\python37\lib\site-packages\statsmodels\base\model.py:508:
ConvergenceWarning: Maximum Likelihood optimization failed to converge. Check mle_retvals
"Check mle_retvals", ConvergenceWarning)Em [213]:
predictions_multi = model_fit.forecast( steps=len(test_multi))
c:\users\naveksha\appdata\local\programs\python\python37\lib\site-packages\statsmodels\tsa\base\tsa_model.py:320:
FutureWarning: Creating a DatetimeIndex by passing range endpoints is deprecated. Use `pandas.date_range` instead.
freq = base_index.freq)
c:\users\naveksha\appdata\local\programs\python\python37\lib\site-packages\statsmodels\tsa\statespace\varmax.py:152:
EstimationWarning: Estimation of VARMA(p,q) models is not generically robust, due especially to identification issues.
EstimationWarning)Em [231]:
plt.plot(train_multi['T'])
plt.plot(test_multi['T'])
plt.plot(predictions_multi.iloc[:,0:1], '--')
plt.show()
plt.plot(train_multi['C6H6(GT)'])
plt.plot(test_multi['C6H6(GT)'])
plt.plot(predictions_multi.iloc[:,1:2], '--')
plt.show()

O código acima mostra como o modelo VARMA pode ser usado para modelar séries temporais multivariadas, embora esse modelo possa não ser o mais adequado em nossos dados.
VARMA com variáveis exógenas (VARMAX)
É uma extensão do modelo VARMA, onde variáveis extras chamadas covariáveis são usadas para modelar a variável primária em que estamos interessados.
Média Móvel Sazonal Auto Regressiva Integrada (SARIMA)
Esta é a extensão do modelo ARIMA para lidar com dados sazonais. Ele divide os dados em componentes sazonais e não sazonais e os modela de maneira semelhante. É caracterizado por 7 parâmetros, para os parâmetros da parte não sazonal (p, d, q) iguais aos do modelo ARIMA e para os parâmetros da parte sazonal (P, D, Q, m) onde 'm' é o número de períodos sazonais e P, D, Q são semelhantes aos parâmetros do modelo ARIMA. Esses parâmetros podem ser calibrados usando busca em grade ou algoritmo genético.
SARIMA com variáveis exógenas (SARIMAX)
Esta é a extensão do modelo SARIMA para incluir variáveis exógenas que nos ajudam a modelar a variável que nos interessa.
Pode ser útil fazer uma análise de correlação nas variáveis antes de colocá-las como variáveis exógenas.
Em [251]:
from scipy.stats.stats import pearsonr
x = train_multi['T'].values
y = train_multi['C6H6(GT)'].values
corr , p = pearsonr(x,y)
print ('Corelation Coefficient =', corr,'\nP-Value =',p)
Corelation Coefficient = 0.9701173437269858
P-Value = 0.0A Correlação de Pearson mostra uma relação linear entre 2 variáveis, para interpretar os resultados, olhamos primeiro para o valor p, se for menor que 0,05 então o valor do coeficiente é significativo, caso contrário, o valor do coeficiente não é significativo. Para um valor p significativo, um valor positivo do coeficiente de correlação indica correlação positiva e um valor negativo indica correlação negativa.
Portanto, para nossos dados, 'temperatura' e 'C6H6' parecem ter uma correlação altamente positiva. Portanto, vamos
Em [297]:
from statsmodels.tsa.statespace.sarimax import SARIMAX
model = SARIMAX(x, exog = y, order = (2, 0, 2), seasonal_order = (2, 0, 1, 1), enforce_stationarity=False, enforce_invertibility = False)
model_fit = model.fit(disp = False)
c:\users\naveksha\appdata\local\programs\python\python37\lib\site-packages\statsmodels\base\model.py:508:
ConvergenceWarning: Maximum Likelihood optimization failed to converge. Check mle_retvals
"Check mle_retvals", ConvergenceWarning)Em [298]:
y_ = test_multi['C6H6(GT)'].values
predicted = model_fit.predict(exog=y_)
test_multi_ = pandas.DataFrame(test)
test_multi_['predictions'] = predicted[0:1871]Em [299]:
plt.plot(train_multi['T'])
plt.plot(test_multi_['T'])
plt.plot(test_multi_.predictions, '--')Fora [299]:
[<matplotlib.lines.Line2D at 0x1eab0191c18>]As previsões aqui parecem ter variações maiores agora, em oposição à modelagem ARIMA univariada.
Desnecessário dizer que o SARIMAX pode ser usado como um modelo ARX, MAX, ARMAX ou ARIMAX, definindo apenas os parâmetros correspondentes para valores diferentes de zero.
Média Móvel Fracionária Auto Regressiva Integrada (FARIMA)
Às vezes, pode acontecer que nossa série não seja estacionária, mas diferenciar com o parâmetro 'd' tomando o valor 1 pode superá-la. Portanto, precisamos diferenciar a série temporal usando um valor fracionário.
No mundo da ciência de dados, não existe um modelo superior; o modelo que funciona com seus dados depende muito do seu conjunto de dados. O conhecimento de vários modelos nos permite escolher um que funcione em nossos dados e fazer experiências com esse modelo para obter os melhores resultados. E os resultados devem ser vistos como gráfico, bem como métricas de erro, às vezes um pequeno erro também pode ser ruim, portanto, traçar e visualizar os resultados é essencial.
No próximo capítulo, veremos outro modelo estatístico, suavização exponencial.
Neste capítulo, falaremos sobre as técnicas envolvidas na suavização exponencial de séries temporais.
Suavização Exponencial Simples
Suavização exponencial é uma técnica para suavizar séries temporais univariadas, atribuindo pesos decrescentes exponencialmente aos dados ao longo de um período de tempo.
Matematicamente, o valor da variável no tempo 't + 1' dado valor no tempo t, y_ (t + 1 | t) é definido como -
$$y_{t+1|t}\:=\:\alpha y_{t}\:+\:\alpha\lgroup1 -\alpha\rgroup y_{t-1}\:+\alpha\lgroup1-\alpha\rgroup^{2}\:y_{t-2}\:+\:...+y_{1}$$
Onde,$0\leq\alpha \leq1$ é o parâmetro de suavização, e
$y_{1},....,y_{t}$ são valores anteriores de tráfego de rede nos tempos 1, 2, 3,…, t.
Este é um método simples para modelar uma série temporal sem tendência ou sazonalidade clara. Mas a suavização exponencial também pode ser usada para séries temporais com tendência e sazonalidade.
Suavização Exponencial Tripla
Suavização Exponencial Tripla (TES) ou método de Holt's Winter, aplica a suavização exponencial três vezes - suavização de nível $l_{t}$, suavização de tendência $b_{t}$e suavização sazonal $S_{t}$, com $\alpha$, $\beta^{*}$ e $\gamma$ como parâmetros de suavização com 'm' como a frequência da sazonalidade, ou seja, o número de estações em um ano.
De acordo com a natureza do componente sazonal, o TES tem duas categorias -
Holt-Winter's Additive Method - Quando a sazonalidade é aditiva por natureza.
Holt-Winter’s Multiplicative Method - Quando a sazonalidade é de natureza multiplicativa.
Para séries temporais não sazonais, temos apenas suavização de tendência e suavização de nível, que é chamada de Método de tendência linear de Holt.
Vamos tentar aplicar a suavização exponencial tripla em nossos dados.
Em [316]:
from statsmodels.tsa.holtwinters import ExponentialSmoothing
model = ExponentialSmoothing(train.values, trend= )
model_fit = model.fit()Em [322]:
predictions_ = model_fit.predict(len(test))Em [325]:
plt.plot(test.values)
plt.plot(predictions_[1:1871])Fora [325]:
[<matplotlib.lines.Line2D at 0x1eab00f1cf8>]
Aqui, treinamos o modelo uma vez com o conjunto de treinamento e, em seguida, continuamos fazendo previsões. Uma abordagem mais realista é treinar novamente o modelo após uma ou mais etapas de tempo. Como obtemos a previsão para o tempo 't + 1' dos dados de treinamento 'até o tempo' t ', a próxima previsão para o tempo' t + 2 'pode ser feita usando os dados de treinamento' até o tempo 't + 1' como o real valor em 't + 1' será conhecido então. Essa metodologia de fazer previsões para uma ou mais etapas futuras e depois treinar novamente o modelo é chamada de previsão contínua ou validação de avanço.
Na modelagem de série temporal, as previsões ao longo do tempo tornam-se cada vez menos precisas e, portanto, é uma abordagem mais realista treinar novamente o modelo com dados reais conforme ele fica disponível para futuras previsões. Como o treinamento de modelos estatísticos não consome muito tempo, a validação direta é a solução preferida para obter resultados mais precisos.
Vamos aplicar a validação de um passo à frente em nossos dados e compará-los com os resultados que obtivemos anteriormente.
Em [333]:
prediction = []
data = train.values
for t In test.values:
model = (ExponentialSmoothing(data).fit())
y = model.predict()
prediction.append(y[0])
data = numpy.append(data, t)Em [335]:
test_ = pandas.DataFrame(test)
test_['predictionswf'] = predictionEm [341]:
plt.plot(test_['T'])
plt.plot(test_.predictionswf, '--')
plt.show()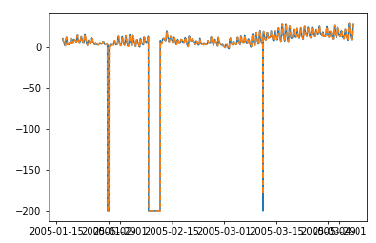
Em [340]:
error = sqrt(metrics.mean_squared_error(test.values,prediction))
print ('Test RMSE for Triple Exponential Smoothing with Walk-Forward Validation: ', error)
Test RMSE for Triple Exponential Smoothing with Walk-Forward Validation: 11.787532205759442Podemos ver que nosso modelo tem um desempenho significativamente melhor agora. Na verdade, a tendência é seguida tão de perto que, no gráfico, as previsões se sobrepõem aos valores reais. Você também pode tentar aplicar a validação direta em modelos ARIMA.
Em 2017, o Facebook abriu o código-fonte do modelo profeta, que era capaz de modelar a série temporal com fortes sazonalidades múltiplas em nível de dia, nível de semana, nível de ano etc. e tendência. Ele tem parâmetros intuitivos que um cientista de dados não tão especialista pode ajustar para melhores previsões. Em sua essência, é um modelo regressivo aditivo que pode detectar pontos de mudança para modelar a série temporal.
O Profeta decompõe a série temporal em componentes de tendência $g_{t}$, sazonalidade $S_{t}$ e feriados $h_{t}$.
$$y_{t}=g_{t}+s_{t}+h_{t}+\epsilon_{t}$$
Onde, $\epsilon_{t}$ é o termo de erro.
Pacotes semelhantes para previsão de séries temporais, como impacto causal e detecção de anomalias, foram introduzidos em R pelo Google e Twitter, respectivamente.
Agora, estamos familiarizados com a modelagem estatística em séries temporais, mas o aprendizado de máquina está na moda agora, por isso é essencial estar familiarizado com alguns modelos de aprendizado de máquina também. Começaremos com o modelo mais popular no domínio das séries temporais - o modelo de Memória de Longo Prazo.
LSTM é uma classe de rede neural recorrente. Portanto, antes de irmos para o LSTM, é essencial entender as redes neurais e as redes neurais recorrentes.
Redes neurais
Uma rede neural artificial é uma estrutura em camadas de neurônios conectados, inspirada por redes neurais biológicas. Não é um algoritmo, mas combinações de vários algoritmos que nos permitem fazer operações complexas nos dados.
Redes Neurais Recorrentes
É uma classe de redes neurais adaptadas para lidar com dados temporais. Os neurônios do RNN possuem um estado / memória celular, e a entrada é processada de acordo com esse estado interno, que é conseguido com a ajuda de loops na rede neural. Existem módulos recorrentes de camadas 'tanh' nos RNNs que lhes permitem reter informações. No entanto, não por muito tempo, por isso precisamos de modelos LSTM.
LSTM
É um tipo especial de rede neural recorrente, capaz de aprender dependências de dados de longo prazo. Isso é obtido porque o módulo recorrente do modelo possui uma combinação de quatro camadas interagindo entre si.

A imagem acima mostra quatro camadas de rede neural em caixas amarelas, operadores pontuais em círculos verdes, entrada em círculos amarelos e o estado da célula em círculos azuis. Um módulo LSTM tem um estado de célula e três portas que fornecem o poder de aprender, desaprender ou reter seletivamente as informações de cada uma das unidades. O estado da célula em LSTM ajuda a informação a fluir através das unidades sem ser alterada, permitindo apenas algumas interações lineares. Cada unidade tem uma entrada, uma saída e uma porta de esquecimento que pode adicionar ou remover as informações do estado da célula. A porta de esquecimento decide quais informações do estado anterior da célula devem ser esquecidas para as quais usa uma função sigmóide. A porta de entrada controla o fluxo de informações para o estado atual da célula, usando uma operação de multiplicação de pontos 'sigmóide' e 'tanh', respectivamente. Finalmente, a porta de saída decide quais informações devem ser passadas para o próximo estado oculto
Agora que entendemos o funcionamento interno do modelo LSTM, vamos implementá-lo. Para entender a implementação do LSTM, começaremos com um exemplo simples - uma linha reta. Vamos ver se o LSTM pode aprender a relação de uma linha reta e predizê-la.
Primeiro, vamos criar o conjunto de dados que descreve uma linha reta.
Em [402]:
x = numpy.arange (1,500,1)
y = 0.4 * x + 30
plt.plot(x,y)Fora [402]:
[<matplotlib.lines.Line2D at 0x1eab9d3ee10>]
Em [403]:
trainx, testx = x[0:int(0.8*(len(x)))], x[int(0.8*(len(x))):]
trainy, testy = y[0:int(0.8*(len(y)))], y[int(0.8*(len(y))):]
train = numpy.array(list(zip(trainx,trainy)))
test = numpy.array(list(zip(trainx,trainy)))Agora que os dados foram criados e divididos em treinar e testar. Vamos converter os dados da série temporal na forma de dados de aprendizado supervisionado de acordo com o valor do período de lookback, que é essencialmente o número de atrasos que são vistos para prever o valor no tempo 't'.
Então, uma série temporal como esta -
time variable_x
t1 x1
t2 x2
: :
: :
T xTQuando o período de lookback é 1, é convertido em -
x1 x2
x2 x3
: :
: :
xT-1 xTEm [404]:
def create_dataset(n_X, look_back):
dataX, dataY = [], []
for i in range(len(n_X)-look_back):
a = n_X[i:(i+look_back), ]
dataX.append(a)
dataY.append(n_X[i + look_back, ])
return numpy.array(dataX), numpy.array(dataY)Em [405]:
look_back = 1
trainx,trainy = create_dataset(train, look_back)
testx,testy = create_dataset(test, look_back)
trainx = numpy.reshape(trainx, (trainx.shape[0], 1, 2))
testx = numpy.reshape(testx, (testx.shape[0], 1, 2))Agora vamos treinar nosso modelo.
Pequenos lotes de dados de treinamento são mostrados para a rede, uma execução de quando todos os dados de treinamento são mostrados ao modelo em lotes e o erro é calculado é chamada de época. As épocas devem ser executadas até o momento em que o erro estiver reduzindo.
Dentro [ ]:
from keras.models import Sequential
from keras.layers import LSTM, Dense
model = Sequential()
model.add(LSTM(256, return_sequences = True, input_shape = (trainx.shape[1], 2)))
model.add(LSTM(128,input_shape = (trainx.shape[1], 2)))
model.add(Dense(2))
model.compile(loss = 'mean_squared_error', optimizer = 'adam')
model.fit(trainx, trainy, epochs = 2000, batch_size = 10, verbose = 2, shuffle = False)
model.save_weights('LSTMBasic1.h5')Em [407]:
model.load_weights('LSTMBasic1.h5')
predict = model.predict(testx)Agora vamos ver como são nossas previsões.
Em [408]:
plt.plot(testx.reshape(398,2)[:,0:1], testx.reshape(398,2)[:,1:2])
plt.plot(predict[:,0:1], predict[:,1:2])Fora [408]:
[<matplotlib.lines.Line2D at 0x1eac792f048>]
Agora, devemos tentar modelar uma onda seno ou cosseno de maneira semelhante. Você pode executar o código fornecido abaixo e brincar com os parâmetros do modelo para ver como os resultados mudam.
Em [409]:
x = numpy.arange (1,500,1)
y = numpy.sin(x)
plt.plot(x,y)Fora [409]:
[<matplotlib.lines.Line2D at 0x1eac7a0b3c8>]
Em [410]:
trainx, testx = x[0:int(0.8*(len(x)))], x[int(0.8*(len(x))):]
trainy, testy = y[0:int(0.8*(len(y)))], y[int(0.8*(len(y))):]
train = numpy.array(list(zip(trainx,trainy)))
test = numpy.array(list(zip(trainx,trainy)))Em [411]:
look_back = 1
trainx,trainy = create_dataset(train, look_back)
testx,testy = create_dataset(test, look_back)
trainx = numpy.reshape(trainx, (trainx.shape[0], 1, 2))
testx = numpy.reshape(testx, (testx.shape[0], 1, 2))Dentro [ ]:
model = Sequential()
model.add(LSTM(512, return_sequences = True, input_shape = (trainx.shape[1], 2)))
model.add(LSTM(256,input_shape = (trainx.shape[1], 2)))
model.add(Dense(2))
model.compile(loss = 'mean_squared_error', optimizer = 'adam')
model.fit(trainx, trainy, epochs = 2000, batch_size = 10, verbose = 2, shuffle = False)
model.save_weights('LSTMBasic2.h5')Em [413]:
model.load_weights('LSTMBasic2.h5')
predict = model.predict(testx)Em [415]:
plt.plot(trainx.reshape(398,2)[:,0:1], trainx.reshape(398,2)[:,1:2])
plt.plot(predict[:,0:1], predict[:,1:2])Fora [415]:
[<matplotlib.lines.Line2D at 0x1eac7a1f550>]
Agora você está pronto para avançar para qualquer conjunto de dados.
É importante para nós quantificar o desempenho de um modelo para usá-lo como feedback e comparação. Neste tutorial, usamos um dos mais populares erros métricos de raiz quadrada média de erro. Existem várias outras métricas de erro disponíveis. Este capítulo os discute resumidamente.
Erro Quadrado Médio
É a média do quadrado da diferença entre os valores previstos e os valores verdadeiros. Sklearn fornece isso como uma função. Ele tem as mesmas unidades dos valores reais e previstos ao quadrado e é sempre positivo.
$$MSE = \frac{1}{n} \displaystyle\sum\limits_{t=1}^n \lgroup y'_{t}\:-y_{t}\rgroup^{2}$$
Onde $y'_{t}$ é o valor previsto,
$y_{t}$ é o valor real, e
n é o número total de valores no conjunto de teste.
É claro pela equação que o MSE é mais penalizador para erros maiores, ou outliers.
Erro de raiz quadrada média
É a raiz quadrada do erro quadrático médio. Também é sempre positivo e está no intervalo dos dados.
$$RMSE = \sqrt{\frac{1}{n} \displaystyle\sum\limits_{t=1}^n \lgroup y'_{t}-y_{t}\rgroup ^2}$$
Onde, $y'_{t}$ é o valor previsto
$y_{t}$ é o valor real, e
n é o número total de valores no conjunto de teste.
Está no poder da unidade e, portanto, é mais interpretável em comparação com MSE. O RMSE também penaliza mais para erros maiores. Usamos a métrica RMSE em nosso tutorial.
Erro Médio Absoluto
É a média da diferença absoluta entre os valores previstos e os valores reais. Tem as mesmas unidades que o valor previsto e verdadeiro e é sempre positivo.
$$MAE = \frac{1}{n}\displaystyle\sum\limits_{t=1}^{t=n} | y'{t}-y_{t}\lvert$$
Onde, $y'_{t}$ é o valor previsto,
$y_{t}$ é o valor real, e
n é o número total de valores no conjunto de teste.
Erro de porcentagem média
É a porcentagem da média da diferença absoluta entre os valores previstos e os valores reais, dividida pelo valor verdadeiro.
$$MAPE = \frac{1}{n}\displaystyle\sum\limits_{t=1}^n\frac{y'_{t}-y_{t}}{y_{t}}*100\: \%$$
Onde, $y'_{t}$ é o valor previsto,
$y_{t}$ é o valor real en é o número total de valores no conjunto de teste.
No entanto, a desvantagem de usar esse erro é que os erros positivos e negativos podem compensar um ao outro. Portanto, é usado o erro percentual médio absoluto.
Erro de porcentagem média absoluta
É a porcentagem da média da diferença absoluta entre os valores previstos e os valores reais, dividida pelo valor verdadeiro.
$$MAPE = \frac{1}{n}\displaystyle\sum\limits_{t=1}^n\frac{|y'_{t}-y_{t}\lvert}{y_{t}}*100\: \%$$
Onde $y'_{t}$ é o valor previsto
$y_{t}$ é o valor real, e
n é o número total de valores no conjunto de teste.
Discutimos a análise de série temporal neste tutorial, o que nos deu a compreensão de que os modelos de série temporal primeiro reconhecem a tendência e a sazonalidade das observações existentes e, em seguida, prevêem um valor com base nessa tendência e sazonalidade. Essa análise é útil em vários campos, como -
Financial Analysis - Inclui previsão de vendas, análise de estoque, análise de mercado de ações, estimativa de preços.
Weather Analysis - Inclui estimativa de temperatura, mudança climática, reconhecimento de mudança sazonal, previsão do tempo.
Network Data Analysis - Inclui previsão do uso da rede, detecção de anomalias ou intrusão, manutenção preditiva.
Healthcare Analysis - Inclui previsão de censo, previsão de benefícios de seguro, monitoramento de paciente.
O aprendizado de máquina lida com vários tipos de problemas. Na verdade, quase todos os campos têm um escopo a ser automatizado ou aprimorado com a ajuda do aprendizado de máquina. Alguns desses problemas, nos quais muito trabalho está sendo feito, são apresentados a seguir.
Dados de série temporal
Esses são os dados que mudam de acordo com o tempo e, portanto, o tempo desempenha um papel crucial nisso, o que discutimos amplamente neste tutorial.
Dados não temporais
São os dados independentes do tempo, e uma grande porcentagem dos problemas de ML são em dados de séries não temporais. Para simplificar, vamos categorizá-lo ainda como -
Numerical Data - Os computadores, ao contrário dos humanos, só entendem números, então todos os tipos de dados são convertidos em dados numéricos para aprendizado de máquina, por exemplo, dados de imagem são convertidos em valores (r, b, g), caracteres são convertidos em códigos ASCII ou palavras são indexados em números, os dados de fala são convertidos em arquivos mfcc contendo dados numéricos.
Image Data - A visão computacional revolucionou o mundo dos computadores, tem várias aplicações no campo da medicina, imagens de satélite etc.
Text Data- O Processamento de Linguagem Natural (NLP) é usado para classificação de texto, detecção de paráfrase e resumo de linguagem. Isso é o que torna o Google e o Facebook inteligentes.
Speech Data- Processamento de fala envolve reconhecimento de fala e compreensão de sentimento. Ele desempenha um papel crucial em transmitir aos computadores as qualidades humanas.