Искусственный интеллект - нечеткие логические системы

Системы нечеткой логики (FLS) производят приемлемый, но определенный вывод в ответ на неполный, неоднозначный, искаженный или неточный (нечеткий) ввод.

Что такое нечеткая логика?

Нечеткая логика (FL) - это метод рассуждений, напоминающий человеческие рассуждения. Подход FL имитирует способ принятия решений человеком, который включает все промежуточные возможности между цифровыми значениями ДА и НЕТ.

Обычный логический блок, который понимает компьютер, принимает точный ввод и выдает определенный вывод как ИСТИНА или ЛОЖЬ, что эквивалентно человеческому ДА или НЕТ.

Изобретатель нечеткой логики Лотфи Заде заметил, что, в отличие от компьютеров, принятие решений человеком включает в себя ряд возможностей между ДА и НЕТ, например:

Определенно ДА

ВОЗМОЖНО ДА

НЕ МОГУ СКАЗАТЬ

ВОЗМОЖНО НЕТ

ОПРЕДЕЛЕННО НЕТ

Нечеткая логика работает на уровнях возможностей ввода для достижения определенного вывода.

Реализация

• Он может быть реализован в системах различного размера и возможностей, от небольших микроконтроллеров до больших сетевых систем управления на базе рабочих станций.

• Он может быть реализован аппаратно, программно или их комбинацией.

Почему нечеткая логика?

Нечеткая логика полезна в коммерческих и практических целях.

• Он может управлять машинами и потребительскими товарами.
• Он может не давать точных рассуждений, но приемлемых рассуждений.
• Нечеткая логика помогает справиться с неопределенностью в инженерии.

Архитектура систем с нечеткой логикой

Он состоит из четырех основных частей, как показано на рисунке -

• Fuzzification Module- Он преобразует входные данные системы, которые представляют собой четкие числа, в нечеткие множества. Он разбивает входной сигнал на пять шагов, таких как -

LP	x - большой положительный
MP	x - средний положительный
S	x маленький
MN	x - средний отрицательный
LN	x - большой минус

• Knowledge Base - В нем хранятся правила IF-THEN, предоставленные экспертами.

• Inference Engine - Он имитирует процесс рассуждений человека, делая нечеткие выводы на входных данных и правилах ЕСЛИ-ТО.

• Defuzzification Module - Преобразует нечеткое множество, полученное механизмом вывода, в четкое значение.

В membership functions work on нечеткие множества переменных.

Функция членства

Функции принадлежности позволяют количественно определять лингвистические термины и графически представлять нечеткое множество. Аmembership functionдля нечеткого множества A на вселенной дискурса X определяется как μ _A : X → [0,1].

Здесь каждому элементу X соответствует значение от 0 до 1. Он называетсяmembership value или degree of membership. Это квантифицирует степень принадлежности элемента в X к нечеткому множеству A .

• Ось x представляет собой вселенную дискурса.
• Ось y представляет собой степени принадлежности к интервалу [0, 1].

Для нечеткого преобразования числового значения может применяться несколько функций принадлежности. Используются простые функции принадлежности, поскольку использование сложных функций не увеличивает точность вывода.

Все функции принадлежности для LP, MP, S, MN, а также LN показаны ниже -

Треугольные формы функции принадлежности наиболее распространены среди различных других форм функций принадлежности, таких как трапецеидальная, одноэлементная и гауссовская.

Здесь напряжение на входе 5-уровневого фаззификатора варьируется от -10 вольт до +10 вольт. Следовательно, соответствующий вывод также изменяется.

Пример системы нечеткой логики

Рассмотрим систему кондиционирования с 5-уровневой системой нечеткой логики. Эта система регулирует температуру кондиционера, сравнивая температуру в помещении и заданное значение температуры.

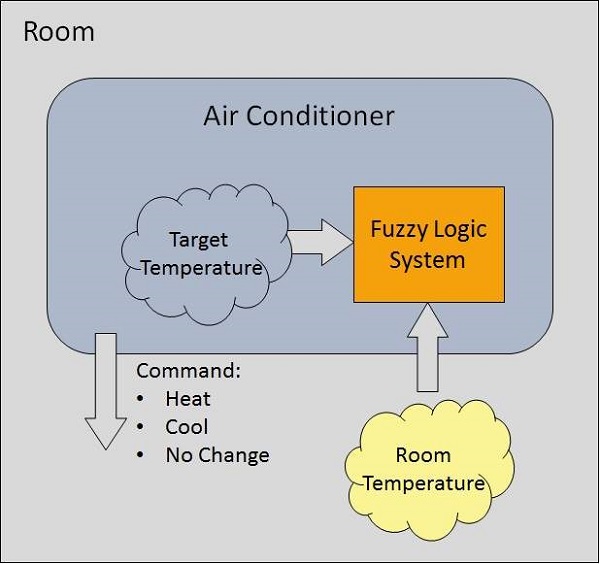
Алгоритм

• Определить лингвистические переменные и термины (начало)
• Постройте для них функции принадлежности. (Начало)
• Построить базу знаний правил (начало)
• Преобразуйте четкие данные в нечеткие наборы данных с помощью функций принадлежности. (фаззификация)
• Оцените правила в базе правил. (Механизм логического вывода)
• Объедините результаты каждого правила. (Механизм логического вывода)
• Преобразуйте выходные данные в нечеткие значения. (дефаззификация)

Развитие

Step 1 − Define linguistic variables and terms

Лингвистические переменные - это входные и выходные переменные в форме простых слов или предложений. Для комнатной температуры термины холодный, теплый, горячий и т. Д. Являются лингвистическими терминами.

Температура (t) = {очень холодно, холодно, тепло, очень тепло, жарко}

Каждый член этого набора - лингвистический термин, который может охватывать некоторую часть общих значений температуры.

Step 2 − Construct membership functions for them

Функции принадлежности переменной температуры, как показано -

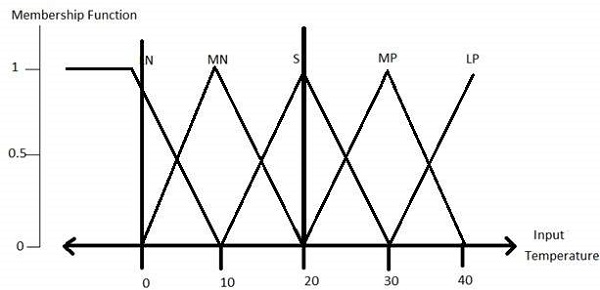
Step3 − Construct knowledge base rules

Создайте матрицу значений температуры в помещении в сравнении со значениями заданной температуры, которые должна обеспечивать система кондиционирования воздуха.

Комнатная температура. / Target	Очень холодно	Холодный	Тепло	Горячей	Очень жарко
Очень холодно	Без изменений	Высокая температура	Высокая температура	Высокая температура	Высокая температура
Холодный	Круто	Без изменений	Высокая температура	Высокая температура	Высокая температура
Тепло	Круто	Круто	Без изменений	Высокая температура	Высокая температура
Горячей	Круто	Круто	Круто	Без изменений	Высокая температура
Очень жарко	Круто	Круто	Круто	Круто	Без изменений

Включите набор правил в базу знаний в виде структур IF-THEN-ELSE.

Sr. No.	Состояние	Действие
1	ЕСЛИ температура = (Холодная ИЛИ Очень_Холодная) И цель = Теплая, ТО	Высокая температура
2	ЕСЛИ температура = (горячая ИЛИ очень горячая) И цель = теплая ТО	Круто
3	ЕСЛИ (температура = тепло) И (цель = тепло) ТО	Без изменений

Step 4 − Obtain fuzzy value

Операции с нечетким множеством выполняют оценку правил. Операции, используемые для OR и AND, - это Max и Min соответственно. Объедините все результаты оценки, чтобы сформировать окончательный результат. Это нечеткое значение.

Step 5 − Perform defuzzification

Затем дефаззификация выполняется в соответствии с функцией принадлежности выходной переменной.

Области применения нечеткой логики

Ключевые области применения нечеткой логики следующие:

Automotive Systems

• Автоматические коробки передач
• Четыре колеса рулевого управления
• Контроль окружающей среды автомобиля

Consumer Electronic Goods

• Hi-Fi системы
• Photocopiers
• Фото- и видеокамеры
• Television

Domestic Goods

• Микроволновые печи
• Refrigerators
• Toasters
• Пылесосы
• Стиральные машины

Environment Control

• Кондиционеры / осушители / обогреватели
• Humidifiers

Преимущества ДУТ

• Математические концепции в рамках нечетких рассуждений очень просты.

• Вы можете изменить ДУТ, просто добавив или удалив правила из-за гибкости нечеткой логики.

• Нечеткая логика. Системы могут принимать неточную, искаженную, зашумленную входную информацию.

• ДУТ легко построить и понять.

• Нечеткая логика - это решение сложных проблем во всех сферах жизни, в том числе в медицине, поскольку она напоминает человеческое мышление и принятие решений.

Недостатки ДУТ

• Системного подхода к проектированию нечетких систем не существует.
• Они понятны только тогда, когда они просты.
• Они подходят для задач, не требующих высокой точности.