Теория автоматов - Краткое руководство
Автоматы - что это?
Термин «Автоматы» происходит от греческого слова «αὐτόματα», что означает «самодействующий». Автомат (во множественном числе «Автоматы») - абстрактное самоходное вычислительное устройство, которое автоматически выполняет заданную последовательность операций.
Автомат с конечным числом состояний называется Finite Automaton (FA) или Finite State Machine (FSM).
Формальное определение конечного автомата
Автомат можно представить в виде набора из пяти (Q, ∑, δ, q 0 , F), где -
Q - конечный набор состояний.
∑ конечный набор символов, называемый alphabet автомата.
δ - функция перехода.
q0- начальное состояние, из которого обрабатывается любой ввод (q 0 ∈ Q).
F представляет собой набор конечных состояний / состояний Q (F ⊆ Q).
Связанные терминологии
Алфавит
Definition - An alphabet - любой конечный набор символов.
Example - ∑ = {a, b, c, d} является alphabet set где 'a', 'b', 'c' и 'd' - symbols.
Строка
Definition - А string - конечная последовательность символов, взятых из ∑.
Example - 'cabcad' - допустимая строка в алфавитном наборе ∑ = {a, b, c, d}
Длина строки
Definition- Это количество символов в строке. (Обозначается|S|).
Examples -
Если S = 'cabcad', | S | = 6
Если | S | = 0, он называется empty string (Обозначается λ или же ε)
Клини Стар
Definition - Звезда Клини, ∑*, является унарным оператором над набором символов или строк, ∑, что дает бесконечное множество всех возможных строк всех возможных длин ∑ включая λ.
Representation- ∑ * = ∑ 0 ∪ ∑ 1 ∪ ∑ 2 ∪ ……. где ∑ p - множество всех возможных строк длины p.
Example - Если ∑ = {a, b}, ∑ * = {λ, a, b, aa, ab, ba, bb, ……… ..}
Клини Закрытие / Плюс
Definition - Набор ∑+ - бесконечное множество всевозможных цепочек всевозможных длин над ∑, исключая λ.
Representation- ∑ + = ∑ 1 ∪ ∑ 2 ∪ ∑ 3 ∪ …….
∑ + = ∑ * - {λ}
Example- Если ∑ = {a, b}, ∑ + = {a, b, aa, ab, ba, bb, ……… ..}
Язык
Definition- Язык - это подмножество ∑ * для некоторого алфавита ∑. Он может быть конечным или бесконечным.
Example - Если язык принимает все возможные строки длины 2 над ∑ = {a, b}, то L = {ab, aa, ba, bb}
Конечный автомат можно разделить на два типа -
- Детерминированный конечный автомат (DFA)
- Недетерминированный конечный автомат (NDFA / NFA)
Детерминированный конечный автомат (DFA)
В DFA для каждого входного символа можно определить состояние, в которое переместится машина. Следовательно, он называетсяDeterministic Automaton. Поскольку он имеет конечное число состояний, машина называетсяDeterministic Finite Machine или же Deterministic Finite Automaton.
Формальное определение DFA
DFA может быть представлен 5-кортежем (Q, ∑, δ, q 0 , F), где -
Q - конечный набор состояний.
∑ конечный набор символов, называемый алфавитом.
δ - функция перехода, где δ: Q × ∑ → Q
q0- начальное состояние, из которого обрабатывается любой ввод (q 0 ∈ Q).
F представляет собой набор конечных состояний / состояний Q (F ⊆ Q).
Графическое представление DFA
DFA представлен орграфами, называемыми state diagram.
- Вершины представляют состояния.
- Дуги, помеченные входным алфавитом, показывают переходы.
- Начальное состояние обозначается пустой единственной входящей дугой.
- Конечное состояние обозначено двойными кружками.
пример
Пусть детерминированный конечный автомат →
- Q = {a, b, c},
- ∑ = {0, 1},
- q 0 = {a},
- F = {c} и
Функция перехода δ, как показано в следующей таблице -
| Настоящее состояние | Следующее состояние для входа 0 | Следующее состояние для входа 1 |
|---|---|---|
| a | а | б |
| b | c | а |
| c | б | c |
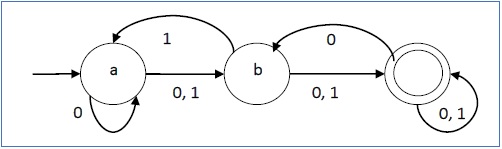
Его графическое представление будет следующим:

В NDFA для определенного входного символа машина может перейти в любую комбинацию состояний машины. Другими словами, невозможно определить точное состояние, в которое переходит машина. Следовательно, он называетсяNon-deterministic Automaton. Поскольку он имеет конечное число состояний, машина называетсяNon-deterministic Finite Machine или же Non-deterministic Finite Automaton.
Формальное определение NDFA
NDFA может быть представлен 5-кортежем (Q, ∑, δ, q 0 , F), где -
Q - конечный набор состояний.
∑ - конечный набор символов, называемых алфавитами.
δ- функция перехода, где δ: Q × ∑ → 2 Q
(Здесь был взят набор мощности Q (2 Q ), потому что в случае NDFA из состояния может происходить переход в любую комбинацию состояний Q)
q0- начальное состояние, из которого обрабатывается любой ввод (q 0 ∈ Q).
F представляет собой набор конечных состояний / состояний Q (F ⊆ Q).
Графическое представление NDFA: (то же, что и DFA)
NDFA представлен орграфами, называемыми диаграммой состояний.
- Вершины представляют состояния.
- Дуги, помеченные входным алфавитом, показывают переходы.
- Начальное состояние обозначается пустой единственной входящей дугой.
- Конечное состояние обозначено двойными кружками.
Example
Пусть недетерминированный конечный автомат →
- Q = {a, b, c}
- ∑ = {0, 1}
- q 0 = {a}
- F = {c}
Функция перехода δ, как показано ниже -
| Настоящее состояние | Следующее состояние для входа 0 | Следующее состояние для входа 1 |
|---|---|---|
| а | а, б | б |
| б | c | а, в |
| c | до н.э | c |
Его графическое представление будет следующим:
DFA против NDFA
В следующей таблице перечислены различия между DFA и NDFA.
| DFA | NDFA |
|---|---|
| Переход от состояния к одному конкретному следующему состоянию для каждого входного символа. Следовательно, это называется детерминированным . | Переход из состояния может происходить в несколько следующих состояний для каждого входного символа. Следовательно, это называется недетерминированным . |
| Переходы пустой строки не видны в DFA. | NDFA разрешает переходы пустых строк. |
| Обратный поиск разрешен в DFA | В NDFA возврат не всегда возможен. |
| Требуется больше места. | Требуется меньше места. |
| Строка принимается DFA, если она переходит в конечное состояние. | Строка принимается NDFA, если хотя бы один из всех возможных переходов заканчивается в конечном состоянии. |
Акцепторы, классификаторы и преобразователи
Акцептор (распознаватель)
Автомат, вычисляющий булеву функцию, называется acceptor. Все состояния акцептора либо принимают, либо отвергают данные ему входные данные.
Классификатор
А classifier имеет более двух конечных состояний и выдает один выход при завершении.
Преобразователь
Автомат, который производит выходные данные на основе текущего ввода и / или предыдущего состояния, называется transducer. Преобразователи могут быть двух типов -
Mealy Machine - Выход зависит как от текущего состояния, так и от текущего входа.
Moore Machine - Вывод зависит только от текущего состояния.
Приемлемость DFA и NDFA
Строка принимается DFA / NDFA, если и только если DFA / NDFA, начиная с начального состояния, заканчивается в принимающем состоянии (любом из конечных состояний) после полного чтения строки.
Строка S принимается DFA / NDFA (Q, ∑, δ, q 0 , F), если и только если
δ*(q0, S) ∈ F
Язык L принято DFA / NDFA
{S | S ∈ ∑* and δ*(q0, S) ∈ F}
Строка S ′ не принимается DFA / NDFA (Q, ∑, δ, q 0 , F), если и только если
δ*(q0, S′) ∉ F
Язык L ', не принятый DFA / NDFA (дополнение принятого языка L), является
{S | S ∈ ∑* and δ*(q0, S) ∉ F}
Example
Рассмотрим DFA, показанный на рисунке 1.3. Из DFA можно получить приемлемые строки.

Строки, принимаемые указанным выше DFA: {0, 00, 11, 010, 101, ...........}
Строки, не принимаемые указанным выше DFA: {1, 011, 111, ........}
Постановка задачи
Позволять X = (Qx, ∑, δx, q0, Fx)быть NDFA, который принимает язык L (X). Мы должны разработать эквивалентный DFAY = (Qy, ∑, δy, q0, Fy) такой, что L(Y) = L(X). Следующая процедура преобразует NDFA в эквивалентный DFA -
Алгоритм
Input - NDFA
Output - Эквивалент DFA
Step 1 - Создать таблицу состояний из заданного NDFA.
Step 2 - Создайте пустую таблицу состояний для возможных входных алфавитов для эквивалентного DFA.
Step 3 - Отметьте начальное состояние DFA как q0 (то же, что и NDFA).
Step 4- Найдите комбинацию состояний {Q 0 , Q 1 , ..., Q n } для каждого возможного входного алфавита.
Step 5 - Каждый раз, когда мы генерируем новое состояние DFA под столбцами входного алфавита, мы должны снова применить шаг 4, в противном случае перейти к шагу 6.
Step 6 - Состояния, которые содержат любое из конечных состояний NDFA, являются конечными состояниями эквивалентного DFA.
пример
Давайте рассмотрим NDFA, показанный на рисунке ниже.

| q | δ (q, 0) | δ (д, 1) |
|---|---|---|
| а | {a, b, c, d, e} | {d, e} |
| б | {c} | {e} |
| c | ∅ | {b} |
| d | {e} | ∅ |
| е | ∅ | ∅ |
Используя описанный выше алгоритм, мы находим его эквивалент DFA. Таблица состояний DFA показана ниже.
| q | δ (q, 0) | δ (д, 1) |
|---|---|---|
| [а] | [a, b, c, d, e] | [d, e] |
| [a, b, c, d, e] | [a, b, c, d, e] | [b, d, e] |
| [d, e] | [e] | ∅ |
| [b, d, e] | [c, e] | [e] |
| [e] | ∅ | ∅ |
| [c, e] | ∅ | [b] |
| [b] | [c] | [e] |
| [c] | ∅ | [b] |
Диаграмма состояний DFA выглядит следующим образом -

Минимизация DFA с использованием теоремы Майхилла-Нероде
Алгоритм
Input - DFA
Output - Минимизированный DFA
Step 1- Нарисуйте таблицу для всех пар состояний (Q i , Q j ), которые не обязательно связаны напрямую [изначально все не отмечены]
Step 2- Рассмотрим каждую пару состояний (Q i , Q j ) в DFA, где Q i ∈ F и Q j ∉ F, или наоборот, и пометьте их. [Здесь F - набор конечных состояний]
Step 3 - Повторяйте этот шаг, пока мы больше не сможем отмечать состояния -
Если есть немаркированная пара (Q i , Q j ), отметьте ее, если пара {δ (Q i , A), δ (Q i , A)} помечена для некоторого входного алфавита.
Step 4- Объедините все немаркированные пары (Q i , Q j ) и сделайте их единым состоянием в сокращенном DFA.
пример
Давайте воспользуемся алгоритмом 2, чтобы минимизировать DFA, показанный ниже.

Step 1 - Рисуем таблицу для всех пар состояний.
| а | б | c | d | е | ж | |
| а | ||||||
| б | ||||||
| c | ||||||
| d | ||||||
| е | ||||||
| ж |
Step 2 - Мы отмечаем пары состояний.
| а | б | c | d | е | ж | |
| а | ||||||
| б | ||||||
| c | ✔ | ✔ | ||||
| d | ✔ | ✔ | ||||
| е | ✔ | ✔ | ||||
| ж | ✔ | ✔ | ✔ |
Step 3- Попробуем обозначить пары состояний зеленой галочкой переходно. Если мы введем 1 для состояния «a» и «f», он перейдет в состояние «c» и «f» соответственно. (c, f) уже отмечен, поэтому мы отметим пару (a, f). Теперь мы вводим 1 в состояние «b» и «f»; он перейдет в состояние «d» и «f» соответственно. (d, f) уже отмечен, поэтому мы отметим пару (b, f).
| а | б | c | d | е | ж | |
| а | ||||||
| б | ||||||
| c | ✔ | ✔ | ||||
| d | ✔ | ✔ | ||||
| е | ✔ | ✔ | ||||
| ж | ✔ | ✔ | ✔ | ✔ | ✔ |
После шага 3 у нас есть комбинации состояний {a, b} {c, d} {c, e} {d, e}, которые не отмечены.
Мы можем рекомбинировать {c, d} {c, e} {d, e} в {c, d, e}
Следовательно, мы получили два комбинированных состояния как - {a, b} и {c, d, e}
Таким образом, окончательный свернутый DFA будет содержать три состояния {f}, {a, b} и {c, d, e}.
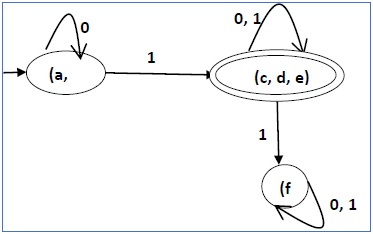
Минимизация DFA с использованием теоремы эквивалентности
Если X и Y - два состояния в DFA, мы можем объединить эти два состояния в {X, Y}, если они не различимы. Два состояния различимы, если существует хотя бы одна строка S, такая, что одно из δ (X, S) и δ (Y, S) принимает, а другое не принимает. Следовательно, ДКА минимален тогда и только тогда, когда все состояния различимы.
Алгоритм 3
Step 1 - Все штаты Q разделены на две перегородки - final states и non-final states и обозначаются P0. Все государства в перегородке равны 0 - й эквивалент. Возьми счетчикk и инициализируйте его с помощью 0.
Step 2- Увеличить k на 1. Для каждого раздела в P k разделить состояния в P k на два раздела, если они k-различимы. Два состояния в этом разделе X и Y являются k-различимыми, если есть входS такой, что δ(X, S) и δ(Y, S) (k-1) -различимы.
Step 3- Если P k ≠ P k-1 , повторите шаг 2, в противном случае перейдите к шагу 4.
Step 4- Объедините k- е эквивалентные множества и сделайте их новыми состояниями сокращенного DFA.
пример
Давайте рассмотрим следующий DFA -

| q | δ (q, 0) | δ (д, 1) |
|---|---|---|
| а | б | c |
| б | а | d |
| c | е | ж |
| d | е | ж |
| е | е | ж |
| ж | ж | ж |
Давайте применим вышеуказанный алгоритм к вышеуказанному DFA -
- P 0 = {(c, d, e), (a, b, f)}
- P 1 = {(c, d, e), (a, b), (f)}
- P 2 = {(c, d, e), (a, b), (f)}
Следовательно, P 1 = P 2 .
В сокращенном DFA есть три состояния. Уменьшенный DFA выглядит следующим образом -
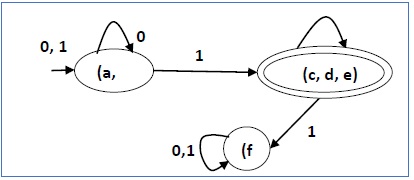
| Q | δ (q, 0) | δ (д, 1) |
|---|---|---|
| (а, б) | (а, б) | (в, г, д) |
| (в, г, д) | (в, г, д) | (е) |
| (е) | (е) | (е) |
Конечные автоматы могут иметь выходы, соответствующие каждому переходу. Есть два типа конечных автоматов, которые генерируют выходные данные:
- Мучная машина
- Машина Мура
Мучная машина
Машина Мили - это конечный автомат, выход которого зависит как от текущего состояния, так и от текущего входа.
Его можно описать набором из 6 (Q, ∑, O, δ, X, q 0 ), где -
Q - конечный набор состояний.
∑ конечный набор символов, называемый входным алфавитом.
O конечный набор символов, называемый выходным алфавитом.
δ - входная переходная функция, где δ: Q × ∑ → Q
X - функция перехода на выходе, где X: Q × ∑ → O
q0- начальное состояние, из которого обрабатывается любой ввод (q 0 ∈ Q).
Таблица состояний машины Mealy показана ниже -
| Настоящее состояние | Следующее состояние | |||
|---|---|---|---|---|
| вход = 0 | input = 1 | |||
| состояние | Вывод | состояние | Вывод | |
| → а | б | х 1 | c | х 1 |
| б | б | х 2 | d | х 3 |
| c | d | х 3 | c | х 1 |
| d | d | х 3 | d | х 2 |
Диаграмма состояний вышеупомянутой машины Мили -

Машина Мура
Машина Мура - это конечный автомат, выходы которого зависят только от текущего состояния.
Машину Мура можно описать набором из 6 (Q, ∑, O, δ, X, q 0 ), где -
Q - конечный набор состояний.
∑ конечный набор символов, называемый входным алфавитом.
O конечный набор символов, называемый выходным алфавитом.
δ - входная переходная функция, где δ: Q × ∑ → Q
X - функция перехода выхода, где X: Q → O
q0- начальное состояние, из которого обрабатывается любой ввод (q 0 ∈ Q).
Таблица состояний машины Мура показана ниже -
| Настоящее состояние | Следующее состояние | Вывод | |
|---|---|---|---|
| Вход = 0 | Вход = 1 | ||
| → а | б | c | х 2 |
| б | б | d | х 1 |
| c | c | d | х 2 |
| d | d | d | х 3 |
Диаграмма состояний вышеупомянутой машины Мура -

Машина Мили против машины Мура
В следующей таблице выделены моменты, которые отличают машину Мили от машины Мура.
| Мучная машина | Машина Мура |
|---|---|
| Выход зависит как от текущего состояния, так и от текущего входа. | Выход зависит только от текущего состояния. |
| Как правило, у него меньше состояний, чем у машины Мура. | Как правило, у него больше состояний, чем у Mealy Machine. |
| Значение выходной функции является функцией переходов и изменений, когда выполняется входная логика для текущего состояния. | Значение выходной функции является функцией текущего состояния и изменений на фронтах тактовых импульсов всякий раз, когда происходят изменения состояния. |
| Аппараты Мили быстрее реагируют на вводимые данные. Обычно они реагируют в одном такте. | В машинах Мура требуется больше логики для декодирования выходных сигналов, что приводит к большим задержкам в цепи. Обычно они реагируют на один такт позже. |
Машина Мура в машину Мили
Алгоритм 4
Input - Машина Мура
Output - Мучная машина
Step 1 - Возьмите пустую таблицу переходов в формате Mealy Machine.
Step 2 - Скопируйте все переходные состояния машины Мура в этот формат таблицы.
Step 3- Проверьте текущие состояния и соответствующие им выходы в таблице состояний машины Мура; если для состояния Q i выходной сигнал равен m, скопируйте его в выходные столбцы таблицы состояний машины Мили, где бы Q i ни появлялся в следующем состоянии.
пример
Давайте рассмотрим следующую машину Мура -
| Настоящее состояние | Следующее состояние | Вывод | |
|---|---|---|---|
| а = 0 | а = 1 | ||
| → а | d | б | 1 |
| б | а | d | 0 |
| c | c | c | 0 |
| d | б | а | 1 |
Теперь применим алгоритм 4, чтобы преобразовать его в Mealy Machine.
Step 1 & 2 -
| Настоящее состояние | Следующее состояние | |||
|---|---|---|---|---|
| а = 0 | а = 1 | |||
| состояние | Вывод | состояние | Вывод | |
| → а | d | б | ||
| б | а | d | ||
| c | c | c | ||
| d | б | а | ||
Step 3 -
| Настоящее состояние | Следующее состояние | |||
|---|---|---|---|---|
| а = 0 | а = 1 | |||
| состояние | Вывод | состояние | Вывод | |
| => а | d | 1 | б | 0 |
| б | а | 1 | d | 1 |
| c | c | 0 | c | 0 |
| d | б | 0 | а | 1 |
Машина Мили к Машине Мура
Алгоритм 5
Input - Мучная машина
Output - Машина Мура
Step 1- Рассчитайте количество различных выходов для каждого состояния (Q i ), которые доступны в таблице состояний машины Мили.
Step 2- Если все выходы Qi одинаковы, скопируйте состояние Q i . Если он имеет п различных выходов, ломают Q I в п состояний как Q в которомn = 0, 1, 2 .......
Step 3 - Если выход начального состояния равен 1, вставьте новое начальное состояние в начало, которое дает 0 выход.
пример
Давайте рассмотрим следующую машину Мили -
| Настоящее состояние | Следующее состояние | |||
|---|---|---|---|---|
| а = 0 | а = 1 | |||
| Следующее состояние | Вывод | Следующее состояние | Вывод | |
| → а | d | 0 | б | 1 |
| б | а | 1 | d | 0 |
| c | c | 1 | c | 0 |
| d | б | 0 | а | 1 |
Здесь состояния «a» и «d» дают только 1 и 0 выходов соответственно, поэтому мы сохраняем состояния «a» и «d». Но состояния «b» и «c» производят разные выходные данные (1 и 0). Итак, делимb в b0, b1 и c в c0, c1.
| Настоящее состояние | Следующее состояние | Вывод | |
|---|---|---|---|
| а = 0 | а = 1 | ||
| → а | d | б 1 | 1 |
| б 0 | а | d | 0 |
| б 1 | а | d | 1 |
| c 0 | c 1 | С 0 | 0 |
| c 1 | c 1 | С 0 | 1 |
| d | б 0 | а | 0 |
В литературном смысле слова грамматики обозначают синтаксические правила разговора на естественных языках. Лингвистика пыталась дать определение грамматики с момента появления естественных языков, таких как английский, санскрит, мандарин и т. Д.
Теория формальных языков находит широкое применение в области компьютерных наук. Noam Chomsky дал математическую модель грамматики в 1956 году, которая эффективна для написания компьютерных языков.
Грамматика
Грамматика G можно формально записать как набор из 4 (N, T, S, P), где -
N или же VN представляет собой набор переменных или нетерминальных символов.
T или же ∑ представляет собой набор терминальных символов.
S - специальная переменная, называемая начальным символом, S ∈ N
P- Правила производства для терминалов и нетерминалов. Правило производства имеет вид α → р, где & alpha ; и β являются строками на V N ∪ Е и меньшей мере , один символ принадлежит к & alpha ; V N .
пример
Грамматика G1 -
({S, A, B}, {a, b}, S, {S → AB, A → a, B → b})
Вот,
S, A, и B нетерминальные символы;
a и b являются терминальными символами
S - начальный символ, S ∈ N
Производство, P : S → AB, A → a, B → b
пример
Грамматика G2 -
(({S, A}, {a, b}, S, {S → aAb, aA → aaAb, A → ε})
Вот,
S and A are Non-terminal symbols.
a and b are Terminal symbols.
ε is an empty string.
S is the Start symbol, S ∈ N
Production P : S → aAb, aA → aaAb, A → ε
Derivations from a Grammar
Strings may be derived from other strings using the productions in a grammar. If a grammar G has a production α → β, we can say that x α y derives x β y in G. This derivation is written as −
x α y ⇒G x β y
Example
Let us consider the grammar −
G2 = ({S, A}, {a, b}, S, {S → aAb, aA → aaAb, A → ε } )
Some of the strings that can be derived are −
S ⇒ aAb using production S → aAb
⇒ aaAbb using production aA → aAb
⇒ aaaAbbb using production aA → aAb
⇒ aaabbb using production A → ε
The set of all strings that can be derived from a grammar is said to be the language generated from that grammar. A language generated by a grammar G is a subset formally defined by
L(G)={W|W ∈ ∑*, S ⇒G W}
If L(G1) = L(G2), the Grammar G1 is equivalent to the Grammar G2.
Example
If there is a grammar
G: N = {S, A, B} T = {a, b} P = {S → AB, A → a, B → b}
Here S produces AB, and we can replace A by a, and B by b. Here, the only accepted string is ab, i.e.,
L(G) = {ab}
Example
Suppose we have the following grammar −
G: N = {S, A, B} T = {a, b} P = {S → AB, A → aA|a, B → bB|b}
The language generated by this grammar −
L(G) = {ab, a2b, ab2, a2b2, ………}
= {am bn | m ≥ 1 and n ≥ 1}
Construction of a Grammar Generating a Language
We’ll consider some languages and convert it into a grammar G which produces those languages.
Example
Problem − Suppose, L (G) = {am bn | m ≥ 0 and n > 0}. We have to find out the grammar G which produces L(G).
Solution
Since L(G) = {am bn | m ≥ 0 and n > 0}
the set of strings accepted can be rewritten as −
L(G) = {b, ab,bb, aab, abb, …….}
Here, the start symbol has to take at least one ‘b’ preceded by any number of ‘a’ including null.
To accept the string set {b, ab, bb, aab, abb, …….}, we have taken the productions −
S → aS , S → B, B → b and B → bB
S → B → b (Accepted)
S → B → bB → bb (Accepted)
S → aS → aB → ab (Accepted)
S → aS → aaS → aaB → aab(Accepted)
S → aS → aB → abB → abb (Accepted)
Thus, we can prove every single string in L(G) is accepted by the language generated by the production set.
Hence the grammar −
G: ({S, A, B}, {a, b}, S, { S → aS | B , B → b | bB })
Example
Problem − Suppose, L (G) = {am bn | m > 0 and n ≥ 0}. We have to find out the grammar G which produces L(G).
Solution −
Since L(G) = {am bn | m > 0 and n ≥ 0}, the set of strings accepted can be rewritten as −
L(G) = {a, aa, ab, aaa, aab ,abb, …….}
Here, the start symbol has to take at least one ‘a’ followed by any number of ‘b’ including null.
To accept the string set {a, aa, ab, aaa, aab, abb, …….}, we have taken the productions −
S → aA, A → aA , A → B, B → bB ,B → λ
S → aA → aB → aλ → a (Accepted)
S → aA → aaA → aaB → aaλ → aa (Accepted)
S → aA → aB → abB → abλ → ab (Accepted)
S → aA → aaA → aaaA → aaaB → aaaλ → aaa (Accepted)
S → aA → aaA → aaB → aabB → aabλ → aab (Accepted)
S → aA → aB → abB → abbB → abbλ → abb (Accepted)
Thus, we can prove every single string in L(G) is accepted by the language generated by the production set.
Hence the grammar −
G: ({S, A, B}, {a, b}, S, {S → aA, A → aA | B, B → λ | bB })
According to Noam Chomosky, there are four types of grammars − Type 0, Type 1, Type 2, and Type 3. The following table shows how they differ from each other −
| Grammar Type | Grammar Accepted | Language Accepted | Automaton |
|---|---|---|---|
| Type 0 | Unrestricted grammar | Recursively enumerable language | Turing Machine |
| Type 1 | Context-sensitive grammar | Context-sensitive language | Linear-bounded automaton |
| Type 2 | Context-free grammar | Context-free language | Pushdown automaton |
| Type 3 | Regular grammar | Regular language | Finite state automaton |
Take a look at the following illustration. It shows the scope of each type of grammar −

Type - 3 Grammar
Type-3 grammars generate regular languages. Type-3 grammars must have a single non-terminal on the left-hand side and a right-hand side consisting of a single terminal or single terminal followed by a single non-terminal.
The productions must be in the form X → a or X → aY
where X, Y ∈ N (Non terminal)
and a ∈ T (Terminal)
The rule S → ε is allowed if S does not appear on the right side of any rule.
Example
X → ε
X → a | aY
Y → bType - 2 Grammar
Type-2 grammars generate context-free languages.
The productions must be in the form A → γ
where A ∈ N (Non terminal)
and γ ∈ (T ∪ N)* (String of terminals and non-terminals).
These languages generated by these grammars are be recognized by a non-deterministic pushdown automaton.
Example
S → X a
X → a
X → aX
X → abc
X → εType - 1 Grammar
Type-1 grammars generate context-sensitive languages. The productions must be in the form
α A β → α γ β
where A ∈ N (Non-terminal)
and α, β, γ ∈ (T ∪ N)* (Strings of terminals and non-terminals)
The strings α and β may be empty, but γ must be non-empty.
The rule S → ε is allowed if S does not appear on the right side of any rule. The languages generated by these grammars are recognized by a linear bounded automaton.
Example
AB → AbBc
A → bcA
B → bType - 0 Grammar
Type-0 grammars generate recursively enumerable languages. The productions have no restrictions. They are any phase structure grammar including all formal grammars.
They generate the languages that are recognized by a Turing machine.
The productions can be in the form of α → β where α is a string of terminals and nonterminals with at least one non-terminal and α cannot be null. β is a string of terminals and non-terminals.
Example
S → ACaB
Bc → acB
CB → DB
aD → DbA Regular Expression can be recursively defined as follows −
ε is a Regular Expression indicates the language containing an empty string. (L (ε) = {ε})
φ is a Regular Expression denoting an empty language. (L (φ) = { })
x is a Regular Expression where L = {x}
If X is a Regular Expression denoting the language L(X) and Y is a Regular Expression denoting the language L(Y), then
X + Y is a Regular Expression corresponding to the language L(X) ∪ L(Y) where L(X+Y) = L(X) ∪ L(Y).
X . Y is a Regular Expression corresponding to the language L(X) . L(Y) where L(X.Y) = L(X) . L(Y)
R* is a Regular Expression corresponding to the language L(R*)where L(R*) = (L(R))*
If we apply any of the rules several times from 1 to 5, they are Regular Expressions.
Some RE Examples
| Regular Expressions | Regular Set |
|---|---|
| (0 + 10*) | L = { 0, 1, 10, 100, 1000, 10000, … } |
| (0*10*) | L = {1, 01, 10, 010, 0010, …} |
| (0 + ε)(1 + ε) | L = {ε, 0, 1, 01} |
| (a+b)* | Set of strings of a’s and b’s of any length including the null string. So L = { ε, a, b, aa , ab , bb , ba, aaa…….} |
| (a+b)*abb | Set of strings of a’s and b’s ending with the string abb. So L = {abb, aabb, babb, aaabb, ababb, …………..} |
| (11)* | Set consisting of even number of 1’s including empty string, So L= {ε, 11, 1111, 111111, ……….} |
| (aa)*(bb)*b | Set of strings consisting of even number of a’s followed by odd number of b’s , so L = {b, aab, aabbb, aabbbbb, aaaab, aaaabbb, …………..} |
| (aa + ab + ba + bb)* | String of a’s and b’s of even length can be obtained by concatenating any combination of the strings aa, ab, ba and bb including null, so L = {aa, ab, ba, bb, aaab, aaba, …………..} |
Any set that represents the value of the Regular Expression is called a Regular Set.
Properties of Regular Sets
Property 1. The union of two regular set is regular.
Proof −
Let us take two regular expressions
RE1 = a(aa)* and RE2 = (aa)*
So, L1 = {a, aaa, aaaaa,.....} (Strings of odd length excluding Null)
and L2 ={ ε, aa, aaaa, aaaaaa,.......} (Strings of even length including Null)
L1 ∪ L2 = { ε, a, aa, aaa, aaaa, aaaaa, aaaaaa,.......}
(Strings of all possible lengths including Null)
RE (L1 ∪ L2) = a* (which is a regular expression itself)
Hence, proved.
Property 2. The intersection of two regular set is regular.
Proof −
Let us take two regular expressions
RE1 = a(a*) and RE2 = (aa)*
So, L1 = { a,aa, aaa, aaaa, ....} (Strings of all possible lengths excluding Null)
L2 = { ε, aa, aaaa, aaaaaa,.......} (Strings of even length including Null)
L1 ∩ L2 = { aa, aaaa, aaaaaa,.......} (Strings of even length excluding Null)
RE (L1 ∩ L2) = aa(aa)* which is a regular expression itself.
Hence, proved.
Property 3. The complement of a regular set is regular.
Proof −
Let us take a regular expression −
RE = (aa)*
So, L = {ε, aa, aaaa, aaaaaa, .......} (Strings of even length including Null)
Complement of L is all the strings that is not in L.
So, L’ = {a, aaa, aaaaa, .....} (Strings of odd length excluding Null)
RE (L’) = a(aa)* which is a regular expression itself.
Hence, proved.
Property 4. The difference of two regular set is regular.
Proof −
Let us take two regular expressions −
RE1 = a (a*) and RE2 = (aa)*
So, L1 = {a, aa, aaa, aaaa, ....} (Strings of all possible lengths excluding Null)
L2 = { ε, aa, aaaa, aaaaaa,.......} (Strings of even length including Null)
L1 – L2 = {a, aaa, aaaaa, aaaaaaa, ....}
(Strings of all odd lengths excluding Null)
RE (L1 – L2) = a (aa)* which is a regular expression.
Hence, proved.
Property 5. The reversal of a regular set is regular.
Proof −
We have to prove LR is also regular if L is a regular set.
Let, L = {01, 10, 11, 10}
RE (L) = 01 + 10 + 11 + 10
LR = {10, 01, 11, 01}
RE (LR) = 01 + 10 + 11 + 10 which is regular
Hence, proved.
Property 6. The closure of a regular set is regular.
Proof −
If L = {a, aaa, aaaaa, .......} (Strings of odd length excluding Null)
i.e., RE (L) = a (aa)*
L* = {a, aa, aaa, aaaa , aaaaa,……………} (Strings of all lengths excluding Null)
RE (L*) = a (a)*
Hence, proved.
Property 7. The concatenation of two regular sets is regular.
Proof −
Let RE1 = (0+1)*0 and RE2 = 01(0+1)*
Here, L1 = {0, 00, 10, 000, 010, ......} (Set of strings ending in 0)
and L2 = {01, 010,011,.....} (Set of strings beginning with 01)
Then, L1 L2 = {001,0010,0011,0001,00010,00011,1001,10010,.............}
Set of strings containing 001 as a substring which can be represented by an RE − (0 + 1)*001(0 + 1)*
Hence, proved.
Identities Related to Regular Expressions
Given R, P, L, Q as regular expressions, the following identities hold −
- ∅* = ε
- ε* = ε
- RR* = R*R
- R*R* = R*
- (R*)* = R*
- RR* = R*R
- (PQ)*P =P(QP)*
- (a+b)* = (a*b*)* = (a*+b*)* = (a+b*)* = a*(ba*)*
- R + ∅ = ∅ + R = R (The identity for union)
- R ε = ε R = R (The identity for concatenation)
- ∅ L = L ∅ = ∅ (The annihilator for concatenation)
- R + R = R (Idempotent law)
- L (M + N) = LM + LN (Left distributive law)
- (M + N) L = ML + NL (Right distributive law)
- ε + RR* = ε + R*R = R*
In order to find out a regular expression of a Finite Automaton, we use Arden’s Theorem along with the properties of regular expressions.
Statement −
Let P and Q be two regular expressions.
If P does not contain null string, then R = Q + RP has a unique solution that is R = QP*
Proof −
R = Q + (Q + RP)P [After putting the value R = Q + RP]
= Q + QP + RPP
When we put the value of R recursively again and again, we get the following equation −
R = Q + QP + QP2 + QP3…..
R = Q (ε + P + P2 + P3 + …. )
R = QP* [As P* represents (ε + P + P2 + P3 + ….) ]
Hence, proved.
Assumptions for Applying Arden’s Theorem
- The transition diagram must not have NULL transitions
- It must have only one initial state
Method
Step 1 − Create equations as the following form for all the states of the DFA having n states with initial state q1.
q1 = q1R11 + q2R21 + … + qnRn1 + ε
q2 = q1R12 + q2R22 + … + qnRn2
…………………………
…………………………
…………………………
…………………………
qn = q1R1n + q2R2n + … + qnRnn
Rij represents the set of labels of edges from qi to qj, if no such edge exists, then Rij = ∅
Step 2 − Solve these equations to get the equation for the final state in terms of Rij
Problem
Construct a regular expression corresponding to the automata given below −

Solution −
Here the initial state and final state is q1.
The equations for the three states q1, q2, and q3 are as follows −
q1 = q1a + q3a + ε (ε move is because q1 is the initial state0
q2 = q1b + q2b + q3b
q3 = q2a
Now, we will solve these three equations −
q2 = q1b + q2b + q3b
= q1b + q2b + (q2a)b (Substituting value of q3)
= q1b + q2(b + ab)
= q1b (b + ab)* (Applying Arden’s Theorem)
q1 = q1a + q3a + ε
= q1a + q2aa + ε (Substituting value of q3)
= q1a + q1b(b + ab*)aa + ε (Substituting value of q2)
= q1(a + b(b + ab)*aa) + ε
= ε (a+ b(b + ab)*aa)*
= (a + b(b + ab)*aa)*
Hence, the regular expression is (a + b(b + ab)*aa)*.
Problem
Construct a regular expression corresponding to the automata given below −

Solution −
Here the initial state is q1 and the final state is q2
Now we write down the equations −
q1 = q10 + ε
q2 = q11 + q20
q3 = q21 + q30 + q31
Now, we will solve these three equations −
q1 = ε0* [As, εR = R]
So, q1 = 0*
q2 = 0*1 + q20
So, q2 = 0*1(0)* [By Arden’s theorem]
Hence, the regular expression is 0*10*.
We can use Thompson's Construction to find out a Finite Automaton from a Regular Expression. We will reduce the regular expression into smallest regular expressions and converting these to NFA and finally to DFA.
Some basic RA expressions are the following −
Case 1 − For a regular expression ‘a’, we can construct the following FA −

Case 2 − For a regular expression ‘ab’, we can construct the following FA −

Case 3 − For a regular expression (a+b), we can construct the following FA −

Case 4 − For a regular expression (a+b)*, we can construct the following FA −

Method
Step 1 Construct an NFA with Null moves from the given regular expression.
Step 2 Remove Null transition from the NFA and convert it into its equivalent DFA.
Problem
Convert the following RA into its equivalent DFA − 1 (0 + 1)* 0
Solution
We will concatenate three expressions "1", "(0 + 1)*" and "0"

Now we will remove the ε transitions. After we remove the ε transitions from the NDFA, we get the following −

It is an NDFA corresponding to the RE − 1 (0 + 1)* 0. If you want to convert it into a DFA, simply apply the method of converting NDFA to DFA discussed in Chapter 1.
Finite Automata with Null Moves (NFA-ε)
A Finite Automaton with null moves (FA-ε) does transit not only after giving input from the alphabet set but also without any input symbol. This transition without input is called a null move.
An NFA-ε is represented formally by a 5-tuple (Q, ∑, δ, q0, F), consisting of
Q − a finite set of states
∑ − a finite set of input symbols
δ − a transition function δ : Q × (∑ ∪ {ε}) → 2Q
q0 − an initial state q0 ∈ Q
F − a set of final state/states of Q (F⊆Q).

The above (FA-ε) accepts a string set − {0, 1, 01}
Removal of Null Moves from Finite Automata
If in an NDFA, there is ϵ-move between vertex X to vertex Y, we can remove it using the following steps −
- Find all the outgoing edges from Y.
- Copy all these edges starting from X without changing the edge labels.
- If X is an initial state, make Y also an initial state.
- If Y is a final state, make X also a final state.
Problem
Convert the following NFA-ε to NFA without Null move.

Solution
Step 1 −
Here the ε transition is between q1 and q2, so let q1 is X and qf is Y.
Here the outgoing edges from qf is to qf for inputs 0 and 1.
Step 2 −
Now we will Copy all these edges from q1 without changing the edges from qf and get the following FA −

Step 3 −
Here q1 is an initial state, so we make qf also an initial state.
So the FA becomes −

Step 4 −
Here qf is a final state, so we make q1 also a final state.
So the FA becomes −

Theorem
Let L be a regular language. Then there exists a constant ‘c’ such that for every string w in L −
|w| ≥ c
We can break w into three strings, w = xyz, such that −
- |y| > 0
- |xy| ≤ c
- For all k ≥ 0, the string xykz is also in L.
Applications of Pumping Lemma
Pumping Lemma is to be applied to show that certain languages are not regular. It should never be used to show a language is regular.
If L is regular, it satisfies Pumping Lemma.
If L does not satisfy Pumping Lemma, it is non-regular.
Method to prove that a language L is not regular
At first, we have to assume that L is regular.
So, the pumping lemma should hold for L.
Use the pumping lemma to obtain a contradiction −
Select w such that |w| ≥ c
Select y such that |y| ≥ 1
Select x such that |xy| ≤ c
Assign the remaining string to z.
Select k such that the resulting string is not in L.
Hence L is not regular.
Problem
Prove that L = {aibi | i ≥ 0} is not regular.
Solution −
At first, we assume that L is regular and n is the number of states.
Let w = anbn. Thus |w| = 2n ≥ n.
By pumping lemma, let w = xyz, where |xy| ≤ n.
Let x = ap, y = aq, and z = arbn, where p + q + r = n, p ≠ 0, q ≠ 0, r ≠ 0. Thus |y| ≠ 0.
Let k = 2. Then xy2z = apa2qarbn.
Number of as = (p + 2q + r) = (p + q + r) + q = n + q
Hence, xy2z = an+q bn. Since q ≠ 0, xy2z is not of the form anbn.
Thus, xy2z is not in L. Hence L is not regular.
If (Q, ∑, δ, q0, F) be a DFA that accepts a language L, then the complement of the DFA can be obtained by swapping its accepting states with its non-accepting states and vice versa.
We will take an example and elaborate this below −

This DFA accepts the language
L = {a, aa, aaa , ............. }
over the alphabet
∑ = {a, b}
So, RE = a+.
Now we will swap its accepting states with its non-accepting states and vice versa and will get the following −

This DFA accepts the language
Ľ = {ε, b, ab ,bb,ba, ............... }
over the alphabet
∑ = {a, b}
Note − If we want to complement an NFA, we have to first convert it to DFA and then have to swap states as in the previous method.
Definition − A context-free grammar (CFG) consisting of a finite set of grammar rules is a quadruple (N, T, P, S) where
N is a set of non-terminal symbols.
T is a set of terminals where N ∩ T = NULL.
P is a set of rules, P: N → (N ∪ T)*, i.e., the left-hand side of the production rule P does have any right context or left context.
S is the start symbol.
Example
- The grammar ({A}, {a, b, c}, P, A), P : A → aA, A → abc.
- The grammar ({S, a, b}, {a, b}, P, S), P: S → aSa, S → bSb, S → ε
- The grammar ({S, F}, {0, 1}, P, S), P: S → 00S | 11F, F → 00F | ε
Generation of Derivation Tree
A derivation tree or parse tree is an ordered rooted tree that graphically represents the semantic information a string derived from a context-free grammar.
Representation Technique
Root vertex − Must be labeled by the start symbol.
Vertex − Labeled by a non-terminal symbol.
Leaves − Labeled by a terminal symbol or ε.
If S → x1x2 …… xn is a production rule in a CFG, then the parse tree / derivation tree will be as follows −

There are two different approaches to draw a derivation tree −
Top-down Approach −
Starts with the starting symbol S
Goes down to tree leaves using productions
Bottom-up Approach −
Starts from tree leaves
Proceeds upward to the root which is the starting symbol S
Derivation or Yield of a Tree
The derivation or the yield of a parse tree is the final string obtained by concatenating the labels of the leaves of the tree from left to right, ignoring the Nulls. However, if all the leaves are Null, derivation is Null.
Example
Let a CFG {N,T,P,S} be
N = {S}, T = {a, b}, Starting symbol = S, P = S → SS | aSb | ε
One derivation from the above CFG is “abaabb”
S → SS → aSbS → abS → abaSb → abaaSbb → abaabb

Sentential Form and Partial Derivation Tree
A partial derivation tree is a sub-tree of a derivation tree/parse tree such that either all of its children are in the sub-tree or none of them are in the sub-tree.
Example
If in any CFG the productions are −
S → AB, A → aaA | ε, B → Bb| ε
the partial derivation tree can be the following −
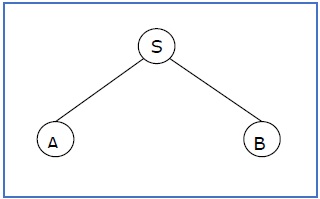
If a partial derivation tree contains the root S, it is called a sentential form. The above sub-tree is also in sentential form.
Leftmost and Rightmost Derivation of a String
Leftmost derivation − A leftmost derivation is obtained by applying production to the leftmost variable in each step.
Rightmost derivation − A rightmost derivation is obtained by applying production to the rightmost variable in each step.
Example
Let any set of production rules in a CFG be
X → X+X | X*X |X| a
over an alphabet {a}.
The leftmost derivation for the string "a+a*a" may be −
X → X+X → a+X → a + X*X → a+a*X → a+a*a
Поэтапный вывод вышеуказанной строки показан ниже -

Крайний правый вывод для указанной выше строки "a+a*a" может быть -
X → X * X → X * a → X + X * a → X + a * a → a + a * a
Поэтапный вывод вышеуказанной строки показан ниже -

Левая и правая рекурсивные грамматики
В контекстно-свободной грамматике G, если есть продукция в виде X → Xa где X нетерминальный и ‘a’ представляет собой цепочку терминалов, она называется left recursive production. Грамматика, имеющая леворекурсивное порождение, называетсяleft recursive grammar.
И если в контекстно-свободной грамматике G, если есть продукция в виде X → aX где X нетерминальный и ‘a’ представляет собой цепочку терминалов, она называется right recursive production. Грамматика, имеющая правильное рекурсивное порождение, называетсяright recursive grammar.
Если контекстно-свободная грамматика G имеет более одного дерева вывода для некоторой строки w ∈ L(G), это называется ambiguous grammar. Существует несколько крайних правых или крайних левых производных для некоторой строки, созданной на основе этой грамматики.
Проблема
Проверить, соответствует ли грамматика G производственным правилам -
X → X + X | Х * Х | Х | а
неоднозначно или нет.
Решение
Давайте узнаем дерево происхождения строки «a + a * a». Имеет два крайних левых вывода.
Derivation 1- Х → Х + Х → а + Х → а + Х * Х → а + а * Х → а + а * а
Parse tree 1 -

Derivation 2- X → X * X → X + X * X → а + X * X → а + а * X → а + а * а
Parse tree 2 -

Поскольку существует два дерева синтаксического анализа для одной строки «a + a * a», грамматика G неоднозначно.
Контекстно-свободные языки closed под -
- Union
- Concatenation
- Клини Стар операция
Союз
Пусть L 1 и L 2 - два контекстно-свободных языка. Тогда L 1 ∪ L 2 также контекстно-свободно.
пример
Пусть L 1 = {a n b n , n> 0}. Соответствующая грамматика G 1 будет иметь P: S1 → aAb | ab
Пусть L 2 = {c m d m , m ≥ 0}. Соответствующая грамматика G 2 будет иметь P: S2 → cBb | ε
Объединение L 1 и L 2 , L = L 1 ∪ L 2 = {a n b n } ∪ {c m d m }
Соответствующая грамматика G будет иметь дополнительную продукцию S → S1 | S2
Конкатенация
Если L 1 и L 2 являются контекстно-свободными языками, то L 1 L 2 также контекстно-свободными.
пример
Объединение языков L 1 и L 2 , L = L 1 L 2 = {a n b n c m d m }
Соответствующая грамматика G будет иметь дополнительную продукцию S → S1 S2
Клини Стар
Если L - контекстно-свободный язык, то L * также контекстно-свободный.
пример
Пусть L = {a n b n , n ≥ 0}. Соответствующая грамматика G будет иметь P: S → aAb | ε
Клини Стар L 1 = {a n b n } *
Соответствующая грамматика G 1 будет иметь дополнительные продукции S1 → SS 1 | ε
Контекстно-свободные языки not closed под -
Intersection - Если L1 и L2 контекстно-свободные языки, то L1 ∩ L2 не обязательно контекстно-свободным.
Intersection with Regular Language - Если L1 - обычный язык, а L2 - контекстно-свободный язык, то L1 ∩ L2 - контекстно-свободный язык.
Complement - Если L1 является контекстно-свободным языком, то L1 'не может быть контекстно-свободным.
В CFG может случиться так, что все производственные правила и символы не нужны для вывода строк. Кроме того, могут быть некоторые нулевые и единичные производства. Устранение этих производств и символов называетсяsimplification of CFGs. Упрощение по существу состоит из следующих шагов -
- Снижение CFG
- Удаление единичных продуктов
- Удаление нулевой продукции
Снижение CFG
CFG сокращаются в две фазы -
Phase 1 - Вывод эквивалентной грамматики, G’, из CFG, G, так что каждая переменная получает некоторую терминальную строку.
Derivation Procedure -
Шаг 1. Включите все символы, W1, которые производят некоторый терминал и инициализируют i=1.
Шаг 2 - Включите все символы, Wi+1, которые производят Wi.
Шаг 3 - Приращение i и повторяйте шаг 2, пока Wi+1 = Wi.
Шаг 4. Включите все производственные правила, в которых есть Wi в этом.
Phase 2 - Вывод эквивалентной грамматики, G”, из CFG, G’, так что каждый символ появляется в форме предложения.
Derivation Procedure -
Шаг 1. Включите начальный символ в Y1 и инициализировать i = 1.
Шаг 2 - Включите все символы, Yi+1, который может быть получен из Yi и включить все применяемые производственные правила.
Шаг 3 - Приращение i и повторяйте шаг 2, пока Yi+1 = Yi.
Проблема
Найдите сокращенную грамматику, эквивалентную грамматике G, имеющую производственные правила, P: S → AC | B, A → a, C → c | BC, E → aA | е
Решение
Phase 1 -
Т = {а, с, е}
W 1 = {A, C, E} из правил A → a, C → c и E → aA
W 2 = {A, C, E} U {S} из правила S → AC
W 3 = {A, C, E, S} U ∅
Поскольку W 2 = W 3 , мы можем получить G 'как -
G '= {{A, C, E, S}, {a, c, e}, P, {S}}
где P: S → AC, A → a, C → c, E → aA | е
Phase 2 -
Y 1 = {S}
Y 2 = {S, A, C} из правила S → AC
Y 3 = {S, A, C, a, c} из правил A → a и C → c
Y 4 = {S, A, C, a, c}
Поскольку Y 3 = Y 4 , мы можем вывести G как -
G ”= {{A, C, S}, {a, c}, P, {S}}
где P: S → AC, A → a, C → c
Удаление единичных продуктов
Любое продукционное правило вида A → B, где A, B ∈ Нетерминал, называется unit production..
Процедура удаления -
Step 1 - удалить A → B, добавить производство A → x к правилу грамматики всякий раз, когда B → xвстречается в грамматике. [x ∈ Terminal, x может быть Null]
Step 2 - Удалить A → B из грамматики.
Step 3 - Повторите с шага 1, пока все единичные продукты не будут удалены.
Problem
Удалите единичное производство из следующего -
S → XY, X → a, Y → Z | б, Z → M, M → N, N → а
Solution -
В грамматике есть 3 единицы продукции -
Y → Z, Z → M и M → N
At first, we will remove M → N.
При N → a добавляем M → a, а M → N удаляем.
Производственный набор становится
S → XY, X → a, Y → Z | б, Z → M, M → a, N → a
Now we will remove Z → M.
При M → a добавляем Z → a, а Z → M удаляем.
Производственный набор становится
S → XY, X → a, Y → Z | б, Z → а, M → а, N → а
Now we will remove Y → Z.
При Z → a добавляем Y → a, а Y → Z удаляем.
Производственный набор становится
S → XY, X → a, Y → a | б, Z → а, M → а, N → а
Теперь Z, M и N недоступны, поэтому мы можем их удалить.
Окончательный CFG не требует единичного производства -
S → XY, X → a, Y → a | б
Удаление нулевой продукции
В CFG нетерминальный символ ‘A’ переменная, допускающая значение NULL, если есть производство A → ε или есть вывод, который начинается с A и, наконец, заканчивается
ε: A → .......… → ε
Процедура удаления
Step 1 - Выявить обнуляемые нетерминальные переменные, которые производят ε.
Step 2 - Для каждого производства A → a, построить все производства A → x где x получается из ‘a’ удалив один или несколько нетерминалов из шага 1.
Step 3 - Объедините исходные постановки с результатом шага 2 и удалите ε - productions.
Problem
Удалите нулевое производство из следующего -
S → ASA | aB | b, A → B, B → b | ∈
Solution -
Есть две переменные с нулевым значением - A и B
At first, we will remove B → ε.
После удаления B → ε, производственный набор становится -
S → ASA | aB | б | a, A ε B | б | & эпсилон, B → b
Now we will remove A → ε.
После удаления A → ε, производственный набор становится -
S → ASA | aB | б | а | SA | AS | S, A → B | б, В → б
Это окончательный производственный набор без нулевого перехода.
CFG находится в нормальной форме Хомского, если продукция находится в следующих формах:
- А → а
- А → ВС
- S → ε
где A, B и C нетерминалы и a является терминальным.
Алгоритм преобразования в нормальную форму Хомского -
Step 1 - Если стартовый символ S происходит с правой стороны, создайте новый начальный символ S’ и новое производство S’→ S.
Step 2- Удалить пустые постановки. (Используя описанный ранее алгоритм удаления нулевой продукции)
Step 3- Удалите единичные производства. (Используя описанный ранее алгоритм удаления продукции Unit)
Step 4 - Заменить каждое производство A → B1…Bn где n > 2 с участием A → B1C где C → B2 …Bn. Повторите этот шаг для всех производств, имеющих два или более символов справа.
Step 5 - Если правая часть продукции находится в форме A → aB где a - терминал и A, B нетерминальные, то производство заменяется на A → XB и X → a. Повторите этот шаг для каждой продукции, которая находится в формеA → aB.
Проблема
Преобразуйте следующий CFG в CNF
S → ASA | aB, A → B | S, B → b | ε
Решение
(1) поскольку S появляется в RHS, мы добавляем новое состояние S0 и S0→S добавляется в производственный набор и становится -
S 0 → S, S → ASA | aB, A → B | S, B → b | ∈
(2) Теперь мы удалим нулевые произведения -
B → ∈ и A → ∈
После удаления B → ε производственный набор становится -
S 0 → S, S → ASA | aB | a, A → B | S | ∈, B → b
После удаления A → ∈ производственный набор становится -
S 0 → S, S → ASA | aB | а | AS | SA | S, A → B | S, B → b
(3) Теперь уберем единицу продукции.
После удаления S → S производственный набор становится -
S 0 → S, S → ASA | aB | а | AS | SA, A → B | S, B → b
После удаления S 0 → S производственный набор становится -
S 0 → ASA | aB | а | AS | SA, S → ASA | aB | а | AS | SA
A → B | S, B → b
После удаления A → B производственный набор становится -
S 0 → ASA | aB | а | AS | SA, S → ASA | aB | а | AS | SA
A → S | б
B → b
После удаления A → S производственный набор становится -
S 0 → ASA | aB | а | AS | SA, S → ASA | aB | а | AS | SA
A → b | ASA | aB | а | AS | SA, B → b
(4) Теперь мы выясним более двух переменных в RHS.
Здесь S 0 → ASA, S → ASA, A → ASA нарушает два нетерминала в RHS
Следовательно, мы применим шаг 4 и шаг 5, чтобы получить следующий окончательный производственный набор, который находится в CNF -
S 0 → AX | aB | а | AS | SA
S → AX | aB | а | AS | SA
A → b | AX | aB | а | AS | SA
B → b
X → SA
(5)Нам нужно изменить продуктивности S 0 → aB, S → aB, A → aB
И окончательная постановка становится -
S 0 → AX | YB | а | AS | SA
S → AX | YB | а | AS | SA
A → b A → b | AX | YB | а | AS | SA
B → b
X → SA
Y → а
CFG находится в нормальной форме Грейбаха, если продукция находится в следующих формах:
А → б
A → bD 1 … D n
S → ε
где A, D 1 , ...., D n - нетерминалы, а b - терминал.
Алгоритм преобразования CFG в нормальную форму Грейбаха
Step 1 - Если стартовый символ S происходит с правой стороны, создайте новый начальный символ S’ и новое производство S’ → S.
Step 2- Удалить пустые постановки. (Используя описанный ранее алгоритм удаления нулевой продукции)
Step 3- Удалите единичные производства. (Используя описанный ранее алгоритм удаления продукции Unit)
Step 4 - Убрать всю прямую и косвенную левую рекурсию.
Step 5 - Сделайте правильную замену продукции, чтобы преобразовать ее в надлежащую форму GNF.
Проблема
Преобразуйте следующий CFG в CNF
S → XY | Xn | п
X → mX | м
Y → Xn | о
Решение
Вот, Sне отображается справа от любого производства, и в наборе производственных правил нет единичных или нулевых производств. Итак, мы можем пропустить Шаг 1 к Шагу 3.
Step 4
Теперь после замены
X в S → XY | Xo | п
с участием
mX | м
мы получаем
S → mXY | МЫ | mXo | мес | п.
И после замены
X в Y → X n | о
с правой стороны
X → mX | м
мы получаем
Y → mXn | мин | о.
К производственному набору добавлены две новые постановки O → o и P → p, а затем мы пришли к окончательному GNF следующим образом:
S → mXY | МЫ | mXC | mC | п
X → mX | м
Y → mXD | мД | о
О → о
P → p
Лемма
Если L это контекстно-свободный язык, есть длина накачки p так что любая строка w ∈ L длины ≥ p можно записать как w = uvxyz, где vy ≠ ε, |vxy| ≤ p, и для всех i ≥ 0, uvixyiz ∈ L.
Применения леммы о накачке
Лемма о накачке используется для проверки того, является ли грамматика контекстно-свободной. Возьмем пример и покажем, как это проверяется.
Проблема
Узнайте, является ли язык L = {xnynzn | n ≥ 1} контекстно-зависимый или нет.
Решение
Позволять Lконтекстно-свободный. Потом,L должно удовлетворять лемме о накачке.
Сначала выберите номер nлеммы о накачке. Затем возьмем z как 0 n 1 n 2 n .
Сломать z в uvwxy, где
|vwx| ≤ n and vx ≠ ε.
Следовательно vwxне может включать одновременно нули и двойки, так как последний 0 и первые 2 находятся на расстоянии не менее (n + 1) позиций. Есть два случая -
Case 1 - vwxне имеет двоек. потомvxимеет только нули и единицы. потомuwy, который должен быть в L, имеет n 2 с, но меньше n 0 или 1 с.
Case 2 - vwx не имеет нулей.
Здесь возникает противоречие.
Следовательно, L не является контекстно-независимым языком.
Базовая структура КПК
Автомат выталкивания - это способ реализации контекстно-свободной грамматики аналогично тому, как мы проектируем DFA для обычной грамматики. DFA может запоминать конечный объем информации, но КПК может запоминать бесконечное количество информации.
По сути, автомат выталкивания - это
"Finite state machine" + "a stack"
Автомат выталкивания состоит из трех компонентов:
- входная лента,
- блок управления, и
- стек бесконечного размера.
Головка стека сканирует верхний символ стека.
Стек выполняет две операции -
Push - вверху добавлен новый символ.
Pop - считывается и удаляется верхний символ.
КПК может читать или не читать входной символ, но он должен читать верхнюю часть стека при каждом переходе.
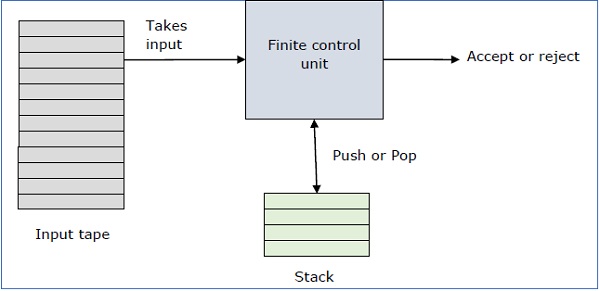
КПК можно формально описать как набор из семи (Q, ∑, S, δ, q 0 , I, F) -
Q конечное число состояний
∑ вводится алфавит
S символы стека
δ - функция перехода: Q × (∑ ∪ {ε}) × S × Q × S *
q0- начальное состояние (q 0 ∈ Q)
I - начальный символ вершины стека (I ∈ S)
F - множество принимающих состояний (F ∈ Q)
На следующей диаграмме показан переход КПК из состояния q 1 в состояние q 2 , обозначенного как a, b → c -

Это означает в состоянии q1, если мы встретим входную строку ‘a’ а верхний символ стека - ‘b’, затем мы поп ‘b’, От себя ‘c’ на вершине стека и перейти в состояние q2.
Терминология, относящаяся к КПК
Мгновенное описание
Мгновенное описание (ID) КПК представлено тройкой (q, w, s), где
q это состояние
w неизрасходованный ввод
s это содержимое стека
Обозначение турникета
Обозначение «турникет» используется для соединения пар идентификаторов, которые представляют один или несколько ходов КПК. Процесс перехода обозначается символом турникета «⊢».
Рассмотрим КПК (Q, ∑, S, δ, q 0 , I, F). Математически переход может быть представлен следующими обозначениями турникета -
(p, aw, Tβ) ⊢ (q, w, αb)Это означает, что при переходе из состояния p заявить q, входной символ ‘a’ потребляется, а вершина стека ‘T’ заменяется новой строкой ‘α’.
Note - Если мы хотим ноль или более ходов КПК, мы должны использовать для этого символ (⊢ *).
Есть два разных способа определить приемлемость КПК.
Приемлемость в конечном состоянии
В допустимости конечного состояния КПК принимает строку, когда после прочтения всей строки КПК находится в конечном состоянии. Из начального состояния мы можем делать ходы, которые заканчиваются в конечном состоянии с любыми значениями стека. Значения стека не имеют значения, пока мы находимся в конечном состоянии.
Для КПК (Q, ∑, S, δ, q 0 , I, F) язык, принимаемый множеством конечных состояний F, -
L (КПК) = {w | (q 0 , w, I) ⊢ * (q, ε, x), q ∈ F}
для любой строки стека ввода x.
Приемлемость пустого стека
Здесь КПК принимает строку, когда после прочтения всей строки КПК опустошает свой стек.
Для КПК (Q, ∑, S, δ, q 0 , I, F) язык, принимаемый пустым стеком, -
L (КПК) = {w | (q 0 , w, I) ⊢ * (q, ε, ε), q ∈ Q}
пример
Создайте КПК, который принимает L = {0n 1n | n ≥ 0}
Решение

Этот язык принимает L = {ε, 01, 0011, 000111, .............................}
Здесь, в этом примере, количество ‘a’ и ‘b’ должно быть таким же.
Изначально ставим специальный символ ‘$’ в пустую стопку.
Тогда в состоянии q2, если мы сталкиваемся с входом 0 и вершиной является Null, мы помещаем 0 в стек. Это может повторяться. И если мы сталкиваемся с входом 1 и вершиной является 0, мы выталкиваем этот 0.
Тогда в состоянии q3, если мы сталкиваемся с входом 1 и вершиной является 0, мы выталкиваем это 0. Это также может повторяться. И если мы сталкиваемся с входом 1 и top равным 0, мы выталкиваем верхний элемент.
Если наверху стека встречается специальный символ «$», он выскакивает и, наконец, переходит в состояние приема q 4 .
пример
Создайте КПК, принимающий L = {ww R | w = (a + b) *}
Solution

Сначала мы помещаем в пустой стек специальный символ «$». В состоянииq2, то wчитается. В состоянииq3, каждый 0 или 1 появляется, когда он соответствует вводу. Если подан какой-либо другой ввод, КПК перейдет в мертвое состояние. Когда мы достигаем этого специального символа '$', мы переходим в состояние принятия.q4.
Если грамматика G не зависит от контекста, мы можем создать эквивалентный недетерминированный КПК, который принимает язык, созданный с помощью контекстно-свободной грамматики G. Парсер может быть построен для грамматикиG.
Кроме того, если P - автомат выталкивания, эквивалентную контекстно-свободную грамматику G можно построить, где
L(G) = L(P)
В следующих двух темах мы обсудим, как преобразовать КПК в CFG и наоборот.
Алгоритм поиска КПК, соответствующего заданному CFG
Input - А CFG, G = (V, T, P, S)
Output- Эквивалентный КПК, P = (Q, ∑, S, δ, q 0 , I, F)
Step 1 - Преобразуйте продукцию CFG в GNF.
Step 2 - КПК будет иметь только одно состояние {q}.
Step 3 - Стартовый символ CFG будет стартовым символом в КПК.
Step 4 - Все нетерминалы CFG будут символами стека КПК, а все терминалы CFG будут входными символами КПК.
Step 5 - Для каждой продукции в форме A → aX где a - терминал и A, X являются комбинацией терминального и нетерминального, сделайте переход δ (q, a, A).
Проблема
Постройте КПК из следующего CFG.
G = ({S, X}, {a, b}, P, S)
где производство -
S → XS | ε , A → aXb | Ab | ab
Решение
Пусть эквивалентный КПК,
P = ({q}, {a, b}, {a, b, X, S}, δ, q, S)
где δ -
δ (q, ε, S) = {(q, XS), (q, ε)}
δ (q, ε, X) = {(q, aXb), (q, Xb), (q, ab)}
δ (q, a, a) = {(q, ε)}
δ (q, 1, 1) = {(q, ε)}
Алгоритм поиска CFG, соответствующего данному КПК
Input - А CFG, G = (V, T, P, S)
Output- Эквивалентный КПК, P = (Q, ∑, S, δ, q 0 , I, F) такой, что нетерминалы грамматики G будут {X wx | W, X ∈ Q} и начальное состояние будет q0, F .
Step 1- Для любых w, x, y, z ∈ Q, m ∈ S и a, b ∈ ∑, если δ (w, a, ε) содержит (y, m) и (z, b, m) содержит (x, ε) добавьте правило продукции X wx → a X yz b в грамматику G.
Step 2- Для каждого w, x, y, z ∈ Q добавьте правило продукции X wx → X wy X yx в грамматику G.
Step 3- Для w ∈ Q добавьте правило продукции X ww → ε в грамматику G.
Синтаксический анализ используется для получения строки с использованием правил грамматики. Он используется для проверки допустимости строки. Компилятор используется для проверки синтаксической правильности строки. Парсер принимает входные данные и строит дерево синтаксического анализа.
Парсер может быть двух типов -
Top-Down Parser - Нисходящий синтаксический анализ начинается сверху с символа начала и выводит строку с использованием дерева синтаксического анализа.
Bottom-Up Parser - Анализ снизу вверх начинается снизу со строки и доходит до начального символа с использованием дерева синтаксического анализа.
Дизайн нисходящего парсера
Для нисходящего синтаксического анализа КПК имеет следующие четыре типа переходов:
Вставьте нетерминал на левой стороне производства в верхнюю часть стопки и протолкните его правую струну.
Если верхний символ стека совпадает с считываемым входным символом, вытолкните его.
Вставьте начальный символ «S» в стопку.
Если входная строка полностью прочитана и стек пуст, перейти в конечное состояние «F».
пример
Разработайте нисходящий синтаксический анализатор для выражения «x + y * z» грамматики G со следующими производственными правилами:
P: S → S + X | X, X → X * Y | Y, Y → (S) | Я бы
Solution
Если КПК равен (Q, ∑, S, δ, q 0 , I, F), то анализ сверху вниз -
(x + y * z, I) ⊢ (x + y * z, SI) ⊢ (x + y * z, S + XI) ⊢ (x + y * z, X + XI)
⊢ (x + y * z, Y + XI) ⊢ (x + y * z, x + XI) ⊢ (+ y * z, + XI) ⊢ (y * z, XI)
⊢ (y * z, X * YI) ⊢ (y * z, y * YI) ⊢ (* z, * YI) ⊢ (z, YI) ⊢ (z, zI) ⊢ (ε, I)
Дизайн парсера снизу вверх
Для восходящего анализа КПК имеет следующие четыре типа переходов:
Вставьте текущий входной символ в стек.
Замените правую часть продукции наверху стопки левой стороной.
Если верх элемента стека совпадает с текущим входным символом, вытолкните его.
Если входная строка полностью прочитана и только если начальный символ «S» остается в стеке, вытолкните его и перейдите в конечное состояние «F».
пример
Разработайте нисходящий синтаксический анализатор для выражения «x + y * z» грамматики G со следующими производственными правилами:
P: S → S + X | X, X → X * Y | Y, Y → (S) | Я бы
Solution
Если КПК - (Q, ∑, S, δ, q 0 , I, F), то восходящий синтаксический анализ -
(x + y * z, I) ⊢ (+ y * z, xI) ⊢ (+ y * z, YI) ⊢ (+ y * z, XI) ⊢ (+ y * z, SI)
⊢ (y * z, + SI) ⊢ (* z, y + SI) ⊢ (* z, Y + SI) ⊢ (* z, X + SI) ⊢ (z, * X + SI)
⊢ (ε, z * X + SI) ⊢ (ε, Y * X + SI) ⊢ (ε, X + SI) ⊢ (ε, SI)
Машина Тьюринга - это принимающее устройство, которое принимает языки (рекурсивно перечисляемый набор), сгенерированные грамматиками типа 0. Он был изобретен в 1936 году Аланом Тьюрингом.
Определение
Машина Тьюринга (TM) - это математическая модель, которая состоит из ленты бесконечной длины, разделенной на ячейки, на которые вводятся данные. Он состоит из головки, которая считывает входную ленту. В регистре состояний хранится состояние машины Тьюринга. После считывания входного символа он заменяется другим символом, его внутреннее состояние изменяется, и он перемещается из одной ячейки вправо или влево. Если TM достигает конечного состояния, входная строка принимается, в противном случае отклоняется.
TM можно формально описать как набор из семи (Q, X, ∑, δ, q 0 , B, F), где -
Q конечный набор состояний
X это ленточный алфавит
∑ это входной алфавит
δ- функция перехода; δ: Q × X → Q × X × {Сдвиг влево, Сдвиг вправо}.
q0 это начальное состояние
B это пустой символ
F это набор конечных состояний
Сравнение с предыдущим автоматом
В следующей таблице показано сравнение того, чем машина Тьюринга отличается от конечного автомата и автомата выталкивания.
| Машина | Структура данных стека | Детерминированный? |
|---|---|---|
| Конечный автомат | NA | да |
| Выталкивающий автомат | Последний пришел - первый ушел (LIFO) | Нет |
| Машина Тьюринга | Бесконечная лента | да |
Пример машины Тьюринга
Машина Тьюринга M = (Q, X, ∑, δ, q 0 , B, F) с
- Q = {q 0 , q 1 , q 2 , q f }
- X = {a, b}
- ∑ = {1}
- q 0 = {q 0 }
- B = пустой символ
- F = {q f }
δ определяется как -
| Символ алфавита ленты | Текущее состояние 'q 0 ' | Текущее состояние 'q 1 ' | Текущее состояние 'q 2 ' |
|---|---|---|---|
| а | 1Rq 1 | 1Lq 0 | 1Lq f |
| б | 1Lq 2 | 1Rq 1 | 1Rq f |
Здесь переход 1Rq 1 означает, что символ записи равен 1, лента перемещается вправо, и следующее состояние - q 1 . Точно так же переход 1Lq 2 подразумевает, что символ записи равен 1, лента перемещается влево и следующее состояние - q 2 .
Временная и пространственная сложность машины Тьюринга
Для машины Тьюринга временная сложность относится к количеству движений ленты, когда машина инициализируется для некоторых входных символов, а пространственная сложность - это количество записанных ячеек ленты.
Сложность времени все разумные функции -
T(n) = O(n log n)
Космическая сложность ТМ -
S(n) = O(n)
TM принимает язык, если он входит в конечное состояние для любой входной строки w. Язык рекурсивно перечислим (генерируется грамматикой типа 0), если он принят машиной Тьюринга.
TM определяет язык, принимает ли он его, и входит в состояние отклонения для любого ввода не на этом языке. Язык рекурсивен, если он определяется машиной Тьюринга.
В некоторых случаях TM не останавливается. Такая ТМ принимает язык, но не решает его.
Разработка машины Тьюринга
Основные принципы проектирования машины Тьюринга были объяснены ниже с помощью пары примеров.
Пример 1
Разработайте TM для распознавания всех строк, состоящих из нечетного числа α.
Solution
Машина Тьюринга M могут быть построены следующими движениями -
Позволять q1 быть начальным состоянием.
Если M в q1; при сканировании α он переходит в состояниеq2 и пишет B (пусто).
Если M в q2; при сканировании α он переходит в состояниеq1 и пишет B (пусто).
Из приведенных выше ходов мы видим, что M входит в государство q1 если он просканирует четное число α и перейдет в состояние q2если он сканирует нечетное количество α. Следовательноq2 единственное принимающее государство.
Следовательно,
M = {{q 1 , q 2 }, {1}, {1, B}, δ, q 1 , B, {q 2 }}
где δ определяется как -
| Символ алфавита ленты | Текущее состояние 'q 1 ' | Текущее состояние 'q 2 ' |
|---|---|---|
| α | BRq 2 | BRq 1 |
Пример 2
Разработайте машину Тьюринга, которая считывает строку, представляющую двоичное число, и стирает все ведущие 0 в строке. Однако, если строка состоит только из 0, она сохраняет один 0.
Solution
Предположим, что входная строка заканчивается пустым символом B на каждом конце строки.
Машина Тьюринга, M, могут быть построены следующими движениями -
Позволять q0 быть начальным состоянием.
Если M в q0, при чтении 0 движется вправо, входит в состояние q1 и стирает 0. При чтении 1 он переходит в состояние q2 и движется вправо.
Если M в q1при чтении 0 он перемещается вправо и стирает 0, т. е. заменяет 0 на B. Достигнув крайней левой единицы, он входитq2и движется вправо. Если он достигает B, т. Е. Строка состоит только из 0, она перемещается влево и переходит в состояниеq3.
Если M в q2, при чтении 0 или 1 он перемещается вправо. Достигнув B, он перемещается влево и входит в состояниеq4. Это подтверждает, что строка состоит только из нулей и единиц.
Если M в q3, он заменяет B на 0, перемещается влево и достигает конечного состояния qf.
Если M в q4при чтении 0 или 1 он перемещается влево. Достигнув начала строки, т. Е. Когда она читает B, она достигает конечного состоянияqf.
Следовательно,
M = {{q 0 , q 1 , q 2 , q 3 , q 4 , q f }, {0,1, B}, {1, B}, δ, q 0 , B, {q f }}
где δ определяется как -
| Символ алфавита ленты | Текущее состояние 'q 0 ' | Текущее состояние 'q 1 ' | Текущее состояние 'q 2 ' | Текущее состояние 'q 3 ' | Текущее состояние 'q 4 ' |
|---|---|---|---|---|---|
| 0 | BRq 1 | BRq 1 | ORq 2 | - | OLq 4 |
| 1 | 1Rq 2 | 1Rq 2 | 1Rq 2 | - | 1лк 4 |
| B | BRq 1 | BLq 3 | BLq 4 | OLq f | BRq f |
Многоленточные машины Тьюринга имеют несколько лент, каждая из которых доступна с отдельной головки. Каждая голова может двигаться независимо от других голов. Первоначально вход находится на ленте 1, а остальные пустые. Сначала первая лента занята входом, а остальные ленты остаются пустыми. Затем машина считывает последовательные символы под своими головами, а TM печатает символ на каждой ленте и перемещает ее головки.

Многоленточную машину Тьюринга можно формально описать как набор из 6 (Q, X, B, δ, q 0 , F), где -
Q конечный набор состояний
X это ленточный алфавит
B это пустой символ
δ отношение состояний и символов, где
δ: Q × X k → Q × (X × {Left_shift, Right_shift, No_shift}) k
где есть k количество лент
q0 это начальное состояние
F это набор конечных состояний
Note - Каждая многоленточная машина Тьюринга имеет эквивалентную одинарную машину Тьюринга.
Многодорожечные машины Тьюринга, особый тип многопленочных машин Тьюринга, содержат несколько дорожек, но только одна головка ленты читает и записывает на все дорожки. Здесь одна головка ленты считывает n символов изnтреки за один шаг. Он принимает рекурсивно перечисляемые языки, как обычная однодорожечная машина Тьюринга с одной лентой.
Многодорожечная машина Тьюринга может быть формально описана как набор из 6 (Q, X, ∑, δ, q 0 , F), где -
Q конечный набор состояний
X это ленточный алфавит
∑ это входной алфавит
δ отношение состояний и символов, где
δ (Q i , [a 1 , a 2 , a 3 , ....]) = (Q j , [b 1 , b 2 , b 3 , ....], Left_shift или Right_shift)
q0 это начальное состояние
F это набор конечных состояний
Note - Для каждой однопутной машины Тьюринга S, существует эквивалентная многодорожечная машина Тьюринга M такой, что L(S) = L(M).
В недетерминированной машине Тьюринга для каждого состояния и символа существует группа действий, которые TM может выполнять. Итак, здесь переходы не детерминированы. Вычисление недетерминированной машины Тьюринга - это дерево конфигураций, к которым можно получить доступ из начальной конфигурации.
Ввод принимается, если есть хотя бы один узел дерева, который является приемлемой конфигурацией, в противном случае он не принимается. Если все ветви вычислительного дерева останавливаются на всех входах, недетерминированная машина Тьюринга называетсяDecider и если для некоторого ввода все ветви отклоняются, ввод также отклоняется.
Недетерминированную машину Тьюринга можно формально определить как набор из шести (Q, X, ∑, δ, q 0 , B, F), где -
Q is a finite set of states
X is the tape alphabet
∑ is the input alphabet
δ is a transition function;
δ : Q × X → P(Q × X × {Left_shift, Right_shift}).
q0 is the initial state
B is the blank symbol
F is the set of final states
A Turing Machine with a semi-infinite tape has a left end but no right end. The left end is limited with an end marker.

It is a two-track tape −
Upper track − It represents the cells to the right of the initial head position.
Lower track − It represents the cells to the left of the initial head position in reverse order.
The infinite length input string is initially written on the tape in contiguous tape cells.
The machine starts from the initial state q0 and the head scans from the left end marker ‘End’. In each step, it reads the symbol on the tape under its head. It writes a new symbol on that tape cell and then it moves the head either into left or right one tape cell. A transition function determines the actions to be taken.
It has two special states called accept state and reject state. If at any point of time it enters into the accepted state, the input is accepted and if it enters into the reject state, the input is rejected by the TM. In some cases, it continues to run infinitely without being accepted or rejected for some certain input symbols.
Note − Turing machines with semi-infinite tape are equivalent to standard Turing machines.
A linear bounded automaton is a multi-track non-deterministic Turing machine with a tape of some bounded finite length.
Length = function (Length of the initial input string, constant c)
Here,
Memory information ≤ c × Input information
The computation is restricted to the constant bounded area. The input alphabet contains two special symbols which serve as left end markers and right end markers which mean the transitions neither move to the left of the left end marker nor to the right of the right end marker of the tape.
A linear bounded automaton can be defined as an 8-tuple (Q, X, ∑, q0, ML, MR, δ, F) where −
Q is a finite set of states
X is the tape alphabet
∑ is the input alphabet
q0 is the initial state
ML is the left end marker
MR is the right end marker where MR ≠ ML
δ is a transition function which maps each pair (state, tape symbol) to (state, tape symbol, Constant ‘c’) where c can be 0 or +1 or -1
F is the set of final states

A deterministic linear bounded automaton is always context-sensitive and the linear bounded automaton with empty language is undecidable..
A language is called Decidable or Recursive if there is a Turing machine which accepts and halts on every input string w. Every decidable language is Turing-Acceptable.

A decision problem P is decidable if the language L of all yes instances to P is decidable.
For a decidable language, for each input string, the TM halts either at the accept or the reject state as depicted in the following diagram −

Example 1
Find out whether the following problem is decidable or not −
Is a number ‘m’ prime?
Solution
Prime numbers = {2, 3, 5, 7, 11, 13, …………..}
Divide the number ‘m’ by all the numbers between ‘2’ and ‘√m’ starting from ‘2’.
If any of these numbers produce a remainder zero, then it goes to the “Rejected state”, otherwise it goes to the “Accepted state”. So, here the answer could be made by ‘Yes’ or ‘No’.
Hence, it is a decidable problem.
Example 2
Given a regular language L and string w, how can we check if w ∈ L?
Solution
Take the DFA that accepts L and check if w is accepted

Some more decidable problems are −
- Does DFA accept the empty language?
- Is L1 ∩ L2 = ∅ for regular sets?
Note −
If a language L is decidable, then its complement L' is also decidable
If a language is decidable, then there is an enumerator for it.
For an undecidable language, there is no Turing Machine which accepts the language and makes a decision for every input string w (TM can make decision for some input string though). A decision problem P is called “undecidable” if the language L of all yes instances to P is not decidable. Undecidable languages are not recursive languages, but sometimes, they may be recursively enumerable languages.

Example
- The halting problem of Turing machine
- The mortality problem
- The mortal matrix problem
- The Post correspondence problem, etc.
Input − A Turing machine and an input string w.
Problem − Does the Turing machine finish computing of the string w in a finite number of steps? The answer must be either yes or no.
Proof − At first, we will assume that such a Turing machine exists to solve this problem and then we will show it is contradicting itself. We will call this Turing machine as a Halting machine that produces a ‘yes’ or ‘no’ in a finite amount of time. If the halting machine finishes in a finite amount of time, the output comes as ‘yes’, otherwise as ‘no’. The following is the block diagram of a Halting machine −

Now we will design an inverted halting machine (HM)’ as −
If H returns YES, then loop forever.
If H returns NO, then halt.
The following is the block diagram of an ‘Inverted halting machine’ −

Further, a machine (HM)2 which input itself is constructed as follows −
- If (HM)2 halts on input, loop forever.
- Else, halt.
Here, we have got a contradiction. Hence, the halting problem is undecidable.
Rice theorem states that any non-trivial semantic property of a language which is recognized by a Turing machine is undecidable. A property, P, is the language of all Turing machines that satisfy that property.
Formal Definition
If P is a non-trivial property, and the language holding the property, Lp , is recognized by Turing machine M, then Lp = {<M> | L(M) ∈ P} is undecidable.
Description and Properties
Property of languages, P, is simply a set of languages. If any language belongs to P (L ∈ P), it is said that L satisfies the property P.
A property is called to be trivial if either it is not satisfied by any recursively enumerable languages, or if it is satisfied by all recursively enumerable languages.
A non-trivial property is satisfied by some recursively enumerable languages and are not satisfied by others. Formally speaking, in a non-trivial property, where L ∈ P, both the following properties hold:
Property 1 − There exists Turing Machines, M1 and M2 that recognize the same language, i.e. either ( <M1>, <M2> ∈ L ) or ( <M1>,<M2> ∉ L )
Property 2 − There exists Turing Machines M1 and M2, where M1 recognizes the language while M2 does not, i.e. <M1> ∈ L and <M2> ∉ L
Proof
Suppose, a property P is non-trivial and φ ∈ P.
Since, P is non-trivial, at least one language satisfies P, i.e., L(M0) ∈ P , ∋ Turing Machine M0.
Let, w be an input in a particular instant and N is a Turing Machine which follows −
On input x
- Run M on w
- If M does not accept (or doesn't halt), then do not accept x (or do not halt)
- If M accepts w then run M0 on x. If M0 accepts x, then accept x.
A function that maps an instance ATM = {<M,w>| M accepts input w} to a N such that
- If M accepts w and N accepts the same language as M0, Then L(M) = L(M0) ∈ p
- If M does not accept w and N accepts φ, Then L(N) = φ ∉ p
Since ATM is undecidable and it can be reduced to Lp, Lp is also undecidable.
The Post Correspondence Problem (PCP), introduced by Emil Post in 1946, is an undecidable decision problem. The PCP problem over an alphabet ∑ is stated as follows −
Given the following two lists, M and N of non-empty strings over ∑ −
M = (x1, x2, x3,………, xn)
N = (y1, y2, y3,………, yn)
We can say that there is a Post Correspondence Solution, if for some i1,i2,………… ik, where 1 ≤ ij ≤ n, the condition xi1 …….xik = yi1 …….yik satisfies.
Example 1
Find whether the lists
M = (abb, aa, aaa) and N = (bba, aaa, aa)
have a Post Correspondence Solution?
Solution
| x1 | x2 | x3 | |
|---|---|---|---|
| M | Abb | aa | aaa |
| N | Bba | aaa | aa |
Here,
x2x1x3 = ‘aaabbaaa’
and y2y1y3 = ‘aaabbaaa’
We can see that
x2x1x3 = y2y1y3
Hence, the solution is i = 2, j = 1, and k = 3.
Example 2
Find whether the lists M = (ab, bab, bbaaa) and N = (a, ba, bab) have a Post Correspondence Solution?
Solution
| x1 | x2 | x3 | |
|---|---|---|---|
| M | ab | bab | bbaaa |
| N | a | ba | bab |
In this case, there is no solution because −
| x2x1x3 | ≠ | y2y1y3 | (Lengths are not same)
Hence, it can be said that this Post Correspondence Problem is undecidable.