Машинное обучение - навыки
Машинное обучение имеет очень большую ширину и требует навыков в нескольких областях. Навыки, которые вам необходимо приобрести, чтобы стать экспертом в области машинного обучения, перечислены ниже:
- Statistics
- Теории вероятностей
- Calculus
- Методы оптимизации
- Visualization
Необходимость различных навыков машинного обучения
Чтобы дать вам краткое представление о том, какие навыки вам необходимо приобрести, давайте обсудим несколько примеров:
Математические обозначения
Большинство алгоритмов машинного обучения в значительной степени основаны на математике. Уровень математики, который вам нужно знать, вероятно, просто начальный уровень. Важно то, что вы должны уметь читать обозначения, которые математики используют в своих уравнениях. Например, если вы умеете читать обозначения и понимать, что они означают, вы готовы к обучению машинному обучению. Если нет, возможно, вам придется освежить свои математические знания.
$$ f_ {AN} (net- \ theta) = \ begin {cases} \ gamma & if \: net- \ theta \ geq \ epsilon \\ net- \ theta & if - \ epsilon <net- \ theta <\ epsilon \\ - \ gamma & if \: net- \ theta \ leq- \ epsilon \ end {case} $$
$$ \ displaystyle \\\ max \ limits _ {\ alpha} \ begin {bmatrix} \ displaystyle \ sum \ limits_ {i = 1} ^ m \ alpha- \ frac {1} {2} \ displaystyle \ sum \ limits_ { i, j = 1} ^ m label ^ \ left (\ begin {array} {c} i \\ \ end {array} \ right) \ cdot \: label ^ \ left (\ begin {array} {c} j \\ \ end {array} \ right) \ cdot \: a_ {i} \ cdot \: a_ {j} \ langle x ^ \ left (\ begin {array} {c} i \\ \ end {array} \ справа), x ^ \ left (\ begin {array} {c} j \\ \ end {array} \ right) \ rangle \ end {bmatrix} $$
$$ f_ {AN} (net- \ theta) = \ left (\ frac {e ^ {\ lambda (net- \ theta)} - e ^ {- \ lambda (net- \ theta)}} {e ^ { \ lambda (net- \ theta)} + e ^ {- \ lambda (net- \ theta)}} \ right) \; $$
Теория вероятности
Вот пример для проверки ваших текущих знаний теории вероятностей: Классификация с условными вероятностями.
$$ p (c_ {i} | x, y) \; = \ frac {p (x, y | c_ {i}) \; p (c_ {i}) \;} {p (x, y) \ ;} $$
С этими определениями мы можем определить правило байесовской классификации -
- Если P (c1 | x, y)> P (c2 | x, y), классом является c1.
- Если P (c1 | x, y) <P (c2 | x, y), классом является c2.
Проблема оптимизации
Вот функция оптимизации
$$ \ displaystyle \\\ max \ limits _ {\ alpha} \ begin {bmatrix} \ displaystyle \ sum \ limits_ {i = 1} ^ m \ alpha- \ frac {1} {2} \ displaystyle \ sum \ limits_ { i, j = 1} ^ m label ^ \ left (\ begin {array} {c} i \\ \ end {array} \ right) \ cdot \: label ^ \ left (\ begin {array} {c} j \\ \ end {array} \ right) \ cdot \: a_ {i} \ cdot \: a_ {j} \ langle x ^ \ left (\ begin {array} {c} i \\ \ end {array} \ справа), x ^ \ left (\ begin {array} {c} j \\ \ end {array} \ right) \ rangle \ end {bmatrix} $$
При соблюдении следующих ограничений -
$$ \ alpha \ geq0 и \: \ displaystyle \ sum \ limits_ {i-1} ^ m \ alpha_ {i} \ cdot \: label ^ \ left (\ begin {array} {c} i \\ \ end {array} \ right) = 0 $$
Если вы можете прочитать и понять вышеизложенное, все готово.
Визуализация
Во многих случаях вам нужно будет понять различные типы графиков визуализации, чтобы понять распределение ваших данных и интерпретировать результаты вывода алгоритма.
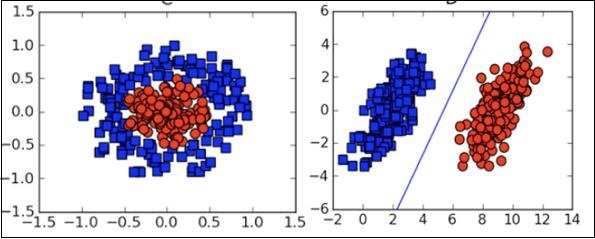
Помимо вышеперечисленных теоретических аспектов машинного обучения, вам необходимы хорошие навыки программирования для кодирования этих алгоритмов.
Итак, что нужно для внедрения машинного обучения? Давайте рассмотрим это в следующей главе.