Моделирование и симуляция - Краткое руководство

Modellingэто процесс представления модели, который включает в себя ее построение и работу. Эта модель похожа на реальную систему, что помогает аналитику прогнозировать влияние изменений в системе. Другими словами, моделирование - это создание модели, которая представляет систему, включая ее свойства. Это акт построения модели.

Simulationсистемы - это работа модели во времени или пространстве, которая помогает анализировать производительность существующей или предлагаемой системы. Другими словами, имитация - это процесс использования модели для изучения производительности системы. Это акт использования модели для моделирования.

История моделирования

Историческая перспектива симуляции перечислена в хронологическом порядке.

1940 - Метод под названием «Монте-Карло» был разработан исследователями (Джон фон Нейман, Станислав Улан, Эдвард Теллер, Герман Кан) и физиками, работающими над проектом на Манхэттене по изучению рассеяния нейтронов.
1960 - Были разработаны первые языки моделирования специального назначения, такие как SIMSCRIPT Гарри Марковицем из корпорации RAND.
1970 - В этот период были начаты исследования математических основ моделирования.
1980 - В этот период были разработаны программы моделирования на базе ПК, графические пользовательские интерфейсы и объектно-ориентированное программирование.
1990 - В этот период были разработаны веб-моделирование, модная анимированная графика, оптимизация на основе моделирования, методы Монте-Карло с цепями Маркова.

Разработка имитационных моделей

Имитационные модели состоят из следующих компонентов: системные объекты, входные переменные, показатели производительности и функциональные отношения. Ниже приведены шаги по разработке имитационной модели.

Step 1 - Определите проблему с существующей системой или установите требования к предлагаемой системе.
Step 2 - Спроектируйте проблему, обращая внимание на существующие системные факторы и ограничения.
Step 3 - Соберите и начните обрабатывать данные системы, наблюдая за ее работоспособностью и результатом.
Step 4 - Разработайте модель с использованием сетевых диаграмм и проверьте ее, используя различные методы проверки.
Step 5 - Проверить модель, сравнив ее производительность в различных условиях с реальной системой.
Step 6 - Создайте документ модели для будущего использования, который подробно включает цели, допущения, входные переменные и характеристики.
Step 7 - Выберите подходящий экспериментальный план в соответствии с требованиями.
Step 8 - Создайте экспериментальные условия на модели и наблюдайте за результатом.

Выполнение анализа моделирования

Ниже приведены шаги для выполнения имитационного анализа.

Step 1 - Подготовьте описание проблемы.
Step 2- Выберите входные переменные и создайте объекты для процесса моделирования. Есть два типа переменных - переменные решения и неконтролируемые переменные. Переменные решения контролируются программистом, тогда как неконтролируемые переменные являются случайными величинами.
Step 3 - Создайте ограничения на переменные решения, назначив их процессу моделирования.
Step 4 - Определите выходные переменные.
Step 5 - Соберите данные из реальной системы для ввода в моделирование.
Step 6 - Разработайте блок-схему, показывающую прогресс процесса моделирования.
Step 7 - Выберите подходящее программное обеспечение для моделирования для запуска модели.
Step 8 - Проверьте имитационную модель, сравнив ее результат с системой реального времени.
Step 9 - Проведите эксперимент на модели, изменив значения переменных, чтобы найти лучшее решение.
Step 10 - Наконец, примените эти результаты в системе реального времени.

Моделирование и симуляция ─ преимущества

Ниже приведены преимущества использования моделирования и моделирования.

Easy to understand - Позволяет понять, как на самом деле работает система, не работая с системами реального времени.
Easy to test - Позволяет вносить изменения в систему и их влияние на результат, не работая в системах реального времени.
Easy to upgrade - Позволяет определять системные требования, применяя различные конфигурации.
Easy to identifying constraints - Позволяет проводить анализ узких мест, вызывающих задержку рабочего процесса, информации и т. Д.
Easy to diagnose problems- Некоторые системы настолько сложны, что сразу понять их взаимодействие непросто. Однако Modeling & Simulation позволяет понять все взаимодействия и проанализировать их влияние. Кроме того, можно изучать новые политики, операции и процедуры, не влияя на реальную систему.

Моделирование и симуляция ─ недостатки

Ниже приведены недостатки использования моделирования и моделирования.

Создание модели - это искусство, требующее знания предметной области, обучения и опыта.
Операции выполняются в системе с использованием случайного числа, поэтому трудно предсказать результат.
Моделирование требует рабочей силы, а это длительный процесс.
Результаты моделирования сложно перевести. Для понимания этого требуются специалисты.
Процесс моделирования дорогостоящий.

Моделирование и симуляция ─ Области применения

Моделирование и имитация могут применяться в следующих областях - военные приложения, обучение и поддержка, проектирование полупроводников, телекоммуникации, проекты и презентации гражданского строительства, а также модели электронного бизнеса.

Кроме того, он используется для изучения внутренней структуры сложной системы, такой как биологическая система. Он используется при оптимизации системного дизайна, такого как алгоритм маршрутизации, сборочная линия и т. Д. Он используется для тестирования новых проектов и политик. Он используется для проверки аналитических решений.

В этой главе мы обсудим различные концепции и классификацию моделирования.

Модели и события

Ниже приведены основные концепции моделирования и симуляции.

Object это сущность, которая существует в реальном мире для изучения поведения модели.
Base Model является гипотетическим объяснением свойств объекта и его поведения, которое справедливо для всей модели.
System - это артикулируемый объект в определенных условиях, существующий в реальном мире.
Experimental Frameиспользуется для изучения системы в реальном мире, таких как экспериментальные условия, аспекты, цели и т. д. Базовая экспериментальная рамка состоит из двух наборов переменных - входных переменных кадра и выходных переменных кадра, которые соответствуют терминалам системы или модели. Входная переменная Frame отвечает за сопоставление входных данных, применяемых к системе или модели. Выходная переменная Frame отвечает за соответствие выходных значений системе или модели.
Lumped Model является точным объяснением системы, которая следует указанным условиям данной экспериментальной рамки.
Verificationэто процесс сравнения двух или более элементов для проверки их точности. В Modeling & Simulation проверка может быть выполнена путем сравнения согласованности программы моделирования и модели с сосредоточенными параметрами, чтобы убедиться в их производительности. Существуют различные способы выполнения процесса проверки, о которых мы поговорим в отдельной главе.
Validationэто процесс сравнения двух результатов. В Modeling & Simulation проверка выполняется путем сравнения экспериментальных измерений с результатами моделирования в контексте экспериментальной рамки. Модель недействительна, если результаты не совпадают. Существуют различные способы выполнения процесса проверки, которые мы рассмотрим в отдельной главе.

Переменные состояния системы

Переменные состояния системы - это набор данных, необходимых для определения внутреннего процесса в системе в заданный момент времени.

В discrete-event model, переменные состояния системы остаются постоянными в течение определенных промежутков времени, а значения изменяются в определенных точках, называемых временами событий.
В continuous-event model, переменные состояния системы определяются результатами дифференциального уравнения, значение которых непрерывно изменяется во времени.

Ниже приведены некоторые из переменных состояния системы -

Entities & Attributes- Сущность представляет собой объект, значение которого может быть статическим или динамическим, в зависимости от процесса с другими сущностями. Атрибуты - это локальные значения, используемые объектом.
Resources- Ресурс - это объект, который одновременно предоставляет услуги одному или нескольким динамическим объектам. Динамический объект может запрашивать одну или несколько единиц ресурса; если принято, то объект может использовать ресурс и освободить после завершения. В случае отклонения объект может присоединиться к очереди.
Lists- Списки используются для представления очередей, используемых объектами и ресурсами. Существуют различные возможности очередей, такие как LIFO, FIFO и т. Д., В зависимости от процесса.
Delay - Это неопределенная продолжительность, вызванная некоторым сочетанием системных условий.

Классификация моделей

Систему можно разделить на следующие категории.

Discrete-Event Simulation Model- В этой модели значения переменных состояния изменяются только в некоторые дискретные моменты времени, когда происходят события. События будут происходить только в определенное время активности и задержки.
Stochastic vs. Deterministic Systems - На стохастические системы не влияет случайность, и их выход не является случайной величиной, тогда как на детерминированные системы влияет случайность, а их выход является случайной величиной.
Static vs. Dynamic Simulation- Статическое моделирование включает модели, на которые не влияет время. Например: Модель Монте-Карло. Динамическое моделирование включает модели, на которые влияет время.
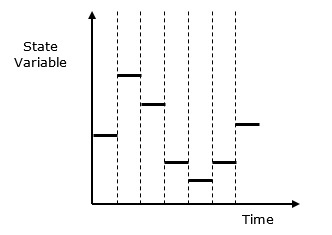
Discrete vs. Continuous Systems- На дискретную систему влияют изменения переменной состояния в дискретный момент времени. Его поведение изображено в следующем графическом представлении.

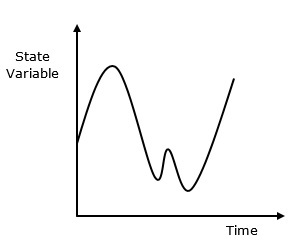
На непрерывную систему влияет переменная состояния, которая непрерывно изменяется во времени. Его поведение изображено в следующем графическом представлении.

Процесс моделирования

Процесс моделирования включает следующие шаги.

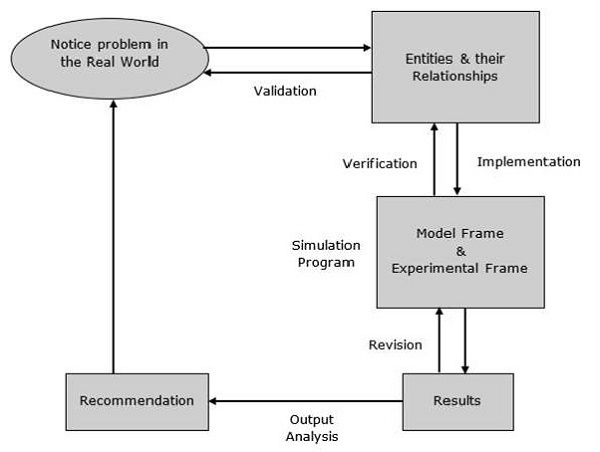
Step 1- Изучите проблему. На этом этапе мы должны понять проблему и соответственно выбрать ее классификацию, например, детерминированную или стохастическую.

Step 2- Создайте модель. На этом этапе мы должны выполнить следующие простые задачи, которые помогут нам разработать модель:

Собирайте данные в соответствии с поведением системы и будущими требованиями.
Проанализируйте особенности системы, ее предположения и необходимые действия, которые необходимо предпринять, чтобы модель была успешной.
Определите имена переменных, функции, их единицы, отношения и их приложения, используемые в модели.
Решите модель, используя подходящую технику, и проверьте результат, используя методы проверки. Затем проверьте результат.
Подготовьте отчет, включающий результаты, интерпретации, выводы и предложения.

Step 3- Дайте рекомендации после завершения всего процесса, связанного с моделью. Он включает в себя инвестиции, ресурсы, алгоритмы, методы и т. Д.

Одна из реальных проблем, с которой сталкивается специалист по моделированию, - это проверка модели. Имитационная модель действительна только в том случае, если модель является точным представлением реальной системы, иначе она недействительна.

Валидация и верификация - два шага в любом проекте моделирования для валидации модели.

Validationэто процесс сравнения двух результатов. В этом процессе нам нужно сравнить представление концептуальной модели с реальной системой. Если сравнение верно, то оно действительно, иначе недействительно.
Verificationэто процесс сравнения двух или более результатов, чтобы убедиться в его точности. В этом процессе мы должны сравнить реализацию модели и связанные с ней данные с концептуальным описанием и спецификациями разработчика.

Методы верификации и валидации

Существуют различные методы, используемые для выполнения верификации и валидации имитационной модели. Ниже приведены некоторые из распространенных методов -

Методы проверки имитационной модели

Ниже приведены способы выполнения проверки имитационной модели.

Используя навыки программирования для написания и отладки программы в подпрограммах.
Используя политику «Структурированного просмотра», согласно которой программу должны читать несколько человек.
Отслеживая промежуточные результаты и сравнивая их с наблюдаемыми результатами.
Путем проверки выходных данных имитационной модели с использованием различных комбинаций входных данных.
Путем сравнения окончательного результата моделирования с аналитическими результатами.

Методы проверки имитационной модели

Step 1- Разработайте модель с высокой достоверностью. Это может быть достигнуто с помощью следующих шагов -

Модель необходимо обсудить с системными экспертами при проектировании.
Модель должна взаимодействовать с клиентом на протяжении всего процесса.
Вывод должен контролироваться системными экспертами.

Step 2- Протестируйте модель на данных допущений. Этого можно достичь, применив данные допущения к модели и проведя ее количественное тестирование. Также можно провести чувствительный анализ, чтобы наблюдать эффект изменения результата, когда во входные данные вносятся существенные изменения.

Step 3- Определите репрезентативные выходные данные имитационной модели. Это может быть достигнуто с помощью следующих шагов -

Определите, насколько близки выходные данные моделирования к выходным данным реальной системы.
Сравнение можно провести с помощью теста Тьюринга. Он представляет данные в системном формате, пояснить который могут только специалисты.
Статистический метод может использоваться для сравнения выходных данных модели с выходными данными реальной системы.

Сравнение модельных данных с реальными данными

После разработки модели необходимо провести сравнение ее выходных данных с реальными данными системы. Ниже приведены два подхода к проведению этого сравнения.

Проверка существующей системы

В этом подходе мы используем реальные входные данные модели для сравнения ее выходных данных с реальными входными данными реальной системы. Этот процесс проверки несложен, однако при его выполнении могут возникнуть некоторые трудности, например, если выходные данные нужно сравнивать со средней продолжительностью, временем ожидания, временем простоя и т. Д., Его можно сравнить с помощью статистических тестов и проверки гипотез. Некоторые из статистических тестов - это тест хи-квадрат, тест Колмогорова-Смирнова, тест Крамера-фон Мизеса и тест моментов.

Проверка модели в первый раз

Считайте, что мы должны описать предлагаемую систему, которой не существует в настоящее время и не существовало в прошлом. Поэтому у нас нет исторических данных, с которыми можно было бы сравнить его производительность. Следовательно, мы должны использовать гипотетическую систему, основанную на предположениях. Следующие полезные указатели помогут сделать его эффективным.

Subsystem Validity- Сама модель может не иметь какой-либо существующей системы для сравнения, но может состоять из известной подсистемы. Каждое из этих утверждений можно проверить отдельно.
Internal Validity - Модель с высокой степенью внутренней дисперсии будет отклонена как стохастическая система с высокой дисперсией из-за ее внутренних процессов, которые будут скрывать изменения на выходе из-за изменений на входе.
Sensitivity Analysis - Он предоставляет информацию о чувствительном параметре в системе, которому нужно уделять повышенное внимание.
Face Validity - Когда модель работает по противоположной логике, ее следует отвергнуть, даже если она ведет себя как реальная система.

В дискретных системах изменения состояния системы прерывистые, и каждое изменение состояния системы называется изменением состояния системы. event. Модель, используемая в моделировании дискретной системы, имеет набор чисел для представления состояния системы, называемыйstate descriptor. В этой главе мы также узнаем о моделировании очередей, которое является очень важным аспектом в моделировании дискретных событий наряду с моделированием системы с разделением времени.

Ниже приводится графическое представление поведения моделирования дискретной системы.

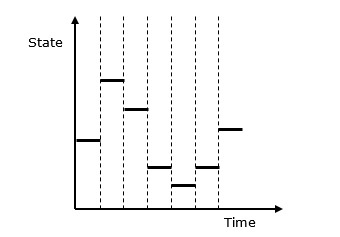
Дискретное моделирование событий ─ Ключевые особенности

Симуляция дискретных событий обычно выполняется с помощью программного обеспечения, разработанного на языках программирования высокого уровня, таких как Паскаль, C ++ или любом специализированном языке моделирования. Ниже приведены пять ключевых функций.

Entities - Это отображение реальных элементов, таких как детали машин.
Relationships - Это значит связывать объекты вместе.
Simulation Executive - Он отвечает за управление временем опережения и выполнение дискретных событий.
Random Number Generator - Это помогает имитировать различные данные, поступающие в имитационную модель.
Results & Statistics - Он проверяет модель и предоставляет показатели ее эффективности.

Представление графика времени

Каждая система зависит от параметра времени. В графическом представлении он упоминается как часы или счетчик времени, и изначально он установлен на ноль. Время обновляется на основе следующих двух факторов:

Time Slicing - Это время, определяемое моделью для каждого события до момента отсутствия какого-либо события.
Next Event- Это событие, определяемое моделью для следующего события, которое должно выполняться вместо временного интервала. Это более эффективно, чем Time Slicing.

Моделирование системы массового обслуживания

Очередь - это комбинация всех объектов в системе, которые обслуживаются, и тех, кто ожидает своей очереди.

Параметры

Ниже приводится список параметров, используемых в системе очередей.

Условное обозначение	Описание
λ	Обозначает скорость прибытия, которая представляет собой количество прибытий в секунду.
Ц	Обозначает среднее время обслуживания для каждого прибытия без учета времени ожидания в очереди.
σTs	Обозначает стандартное отклонение времени обслуживания.
ρ	Обозначает использование времени сервера, как когда он простаивает, так и когда он занят.
ты	Обозначает интенсивность движения
р	Обозначает среднее значение элементов в системе
р	Обозначает общее количество элементов в системе
Тр	Обозначает среднее время нахождения элемента в системе.
TR	Обозначает общее время элемента в системе
σr	Обозначает стандартное отклонение r
σTr	Обозначает стандартное отклонение Tr
ш	Обозначает среднее количество элементов, ожидающих в очереди.
σw	Обозначает стандартное отклонение w
Tw	Обозначает среднее время ожидания всех предметов
Тд	Обозначает среднее время ожидания элементов, ожидающих в очереди.
N	Обозначает количество серверов в системе
mx (y)	Обозначает y- ^й процентиль, который означает значение y, ниже которого x встречается в y процентов случаев.

Очередь одного сервера

Это простейшая система очередей, представленная на следующем рисунке. Центральным элементом системы является сервер, который обслуживает подключенные устройства или объекты. Элементы запроса к системе для обслуживания, если сервер простаивает. Затем он обслуживается немедленно, иначе он присоединяется к очереди ожидания. После того, как задача выполнена сервером, элемент улетает.

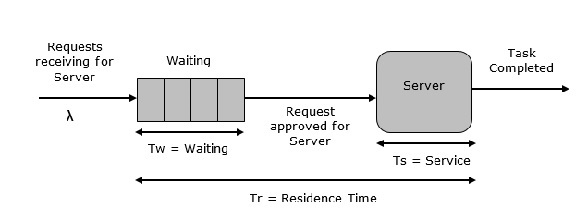
Многосерверная очередь

Как следует из названия, система состоит из нескольких серверов и общей очереди для всех элементов. Когда какой-либо элемент запрашивает сервер, он выделяется, если доступен хотя бы один сервер. В противном случае очередь начинает запускаться, пока сервер не освободится. В этой системе мы предполагаем, что все серверы идентичны, т.е. нет разницы, какой сервер выбран для какого элемента.

Есть исключение по утилизации. ПозволятьN быть идентичными серверами, тогда ρзагрузка каждого сервера. РассматриватьNρбыть использованием всей системы; тогда максимальное использованиеN*100%, а максимальная скорость ввода -

$ λmax = \ frac {\ text {N}} {\ text {T} s} $

Отношения в очереди

В следующей таблице показаны некоторые основные отношения очередей.

Общие условия	Один сервер	Мульти сервер
r = λTr формула Литтла	ρ = λTs	ρ = λTs / N
w = λTw формула Литтла	г = ш + р	u = λTs = ρN
Тр = Tw + Ts		г = w + Nρ

Моделирование системы разделения времени

Система разделения времени разработана таким образом, что каждый пользователь использует небольшую часть времени, совместно используемого в системе, что приводит к одновременному использованию системы несколькими пользователями. Переключение каждого пользователя происходит так быстро, что каждый пользователь чувствует, что использует свою собственную систему. Он основан на концепции планирования ЦП и мультипрограммирования, при которой несколько ресурсов могут быть эффективно использованы путем одновременного выполнения нескольких заданий в системе.

Example - Система моделирования SimOS.

Он разработан Стэнфордским университетом для изучения сложных конструкций компьютерного оборудования, анализа производительности приложений и изучения операционных систем. SimOS содержит программную симуляцию всех аппаратных компонентов современных компьютерных систем, то есть процессоров, модулей управления памятью (MMU), кэшей и т. Д.

Непрерывная система - это система, в которой важные действия системы выполняются плавно, без каких-либо задержек, то есть без очереди событий, без сортировки моделирования времени и т. Д. Когда непрерывная система моделируется математически, ее переменные, представляющие атрибуты, управляются непрерывными функциями .

Что такое непрерывное моделирование?

Непрерывное моделирование - это тип моделирования, в котором переменные состояния непрерывно изменяются во времени. Ниже приводится графическое представление его поведения.

Зачем использовать непрерывное моделирование?

Мы должны использовать непрерывное моделирование, так как оно зависит от известных нам дифференциальных уравнений различных параметров, связанных с системой, и их оценочных результатов.

Области применения

Непрерывное моделирование используется в следующих секторах. В гражданском строительстве для строительства насыпей плотин и тоннелей. В военных приложениях для моделирования траектории полета ракеты, моделирования тренировок истребителей, а также проектирования и тестирования интеллектуального контроллера для подводных аппаратов.

В области логистики для проектирования платных станций, анализа пассажиропотока в терминале аэропорта и упреждающей оценки расписания полетов. В развитии бизнеса для планирования разработки продукта, планирования управления персоналом и анализа рынка.

Моделирование методом Монте-Карло - это компьютеризированный математический метод для генерации данных случайной выборки на основе некоторого известного распределения для численных экспериментов. Этот метод применяется для количественного анализа рисков и принятия решений. Этот метод используют профессионалы различного профиля, такие как финансы, управление проектами, энергетика, производство, инжиниринг, исследования и разработки, страхование, нефть и газ, транспорт и т. Д.

Этот метод впервые был использован учеными, работавшими над атомной бомбой в 1940 году. Этот метод можно использовать в тех ситуациях, когда нам нужно сделать оценку и принять неопределенные решения, такие как прогнозы погоды.

Моделирование методом Монте-Карло ─ важные характеристики

Ниже приведены три важных характеристики метода Монте-Карло:

Его вывод должен генерировать случайные выборки.
Его входное распределение должно быть известно.
Его результат должен быть известен при проведении эксперимента.

Моделирование методом Монте-Карло ─ преимущества

Легко реализовать.
Предоставляет статистическую выборку для численных экспериментов с использованием компьютера.
Предлагает приблизительное решение математических задач.
Может использоваться как для стохастических, так и для детерминированных задач.

Моделирование Монте-Карло ─ Недостатки

Это отнимает много времени, так как необходимо создать большое количество выборок, чтобы получить желаемый результат.
Результаты этого метода - только приближение к истинным значениям, а не к точным.

Метод моделирования Монте-Карло ─ блок-схема

На следующем рисунке показана обобщенная блок-схема моделирования Монте-Карло.

Цель базы данных в Modeling & Simulation - предоставить представление данных и их взаимосвязь для целей анализа и тестирования. Первая модель данных была представлена в 1980 году Эдгаром Коддом. Ниже были основные особенности модели.

База данных - это набор различных объектов данных, которые определяют информацию и их отношения.
Правила предназначены для определения ограничений данных в объектах.
К объектам можно применять операции для получения информации.

Первоначально моделирование данных было основано на концепции сущностей и отношений, в которых сущности являются типами информации данных, а отношения представляют связи между сущностями.

Последняя концепция моделирования данных - это объектно-ориентированный дизайн, в котором сущности представлены в виде классов, которые используются в качестве шаблонов в компьютерном программировании. Класс, имеющий свое имя, атрибуты, ограничения и отношения с объектами других классов.

Его основное представление выглядит так -

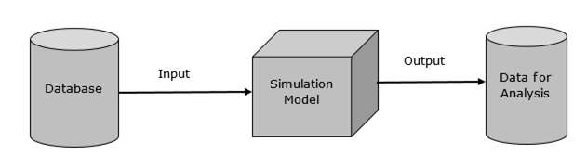
Представление данных

Представление данных для событий

Событие моделирования имеет свои атрибуты, такие как имя события и связанная с ним информация о времени. Он представляет выполнение предоставленного моделирования с использованием набора входных данных, связанных с параметром входного файла, и предоставляет свой результат в виде набора выходных данных, хранящихся в нескольких файлах, связанных с файлами данных.

Представление данных для входных файлов

Каждый процесс моделирования требует другого набора входных данных и связанных с ними значений параметров, которые представлены во входном файле данных. Входной файл связан с программным обеспечением, которое обрабатывает моделирование. Модель данных представляет файлы, на которые есть ссылки, путем ассоциации с файлом данных.

Представление данных для выходных файлов

Когда процесс моделирования завершен, он создает различные выходные файлы, и каждый выходной файл представляется как файл данных. У каждого файла есть свое имя, описание и универсальный фактор. Файл данных делится на два файла. Первый файл содержит числовые значения, а второй файл содержит описательную информацию о содержании числового файла.

Нейронные сети в моделировании и симуляции

Нейронная сеть - это ветвь искусственного интеллекта. Нейронная сеть - это сеть из множества процессоров, называемых модулями, каждый из которых имеет небольшую локальную память. Каждый блок связан однонаправленными каналами связи, называемыми соединениями, которые несут числовые данные. Каждое устройство работает только со своими локальными данными и с входными данными, которые они получают от соединений.

История

Историческая перспектива симуляции перечислена в хронологическом порядке.

Первая нейронная модель была разработана в 1940 компании McCulloch & Pitts.

В 1949Дональд Хебб написал книгу «Организация поведения», в которой указал на концепцию нейронов.

В 1950С развитием компьютеров стало возможным моделировать эти теории. Это сделали исследовательские лаборатории IBM. Однако попытка провалилась, и более поздние попытки увенчались успехом.

В 1959Бернард Видроу и Марсиан Хофф разработали модели под названием ADALINE и MADALINE. Эти модели имеют несколько элементов ADAptive LINear. MADALINE была первой нейронной сетью, которая была применена к реальной проблеме.

В 1962, модель персептрона была разработана Розенблаттом, способная решать простые задачи классификации образов.

В 1969, Minsky & Papert представили математическое доказательство ограничений модели персептрона в вычислениях. Было сказано, что модель персептрона не может решить проблему X-OR. Подобные недостатки привели к временному упадку нейронных сетей.

В 1982Джон Хопфилд из Калифорнийского технологического института представил в Национальной академии наук свои идеи на бумаге по созданию машин с использованием двунаправленных линий. Раньше использовались однонаправленные линии.

Когда традиционные методы искусственного интеллекта с использованием символических методов потерпели неудачу, возникает необходимость в использовании нейронных сетей. Нейронные сети имеют свои массивные методы параллелизма, которые обеспечивают вычислительную мощность, необходимую для решения таких задач.

Области применения

Нейронная сеть может использоваться в машинах для синтеза речи, для распознавания образов, для обнаружения диагностических проблем, в роботизированных панелях управления и медицинском оборудовании.

Нечеткое множество в моделировании и симуляции

Как обсуждалось ранее, каждый процесс непрерывного моделирования зависит от дифференциальных уравнений и их параметров, таких как a, b, c, d> 0. Как правило, точечные оценки вычисляются и используются в модели. Однако иногда эти оценки являются неопределенными, поэтому нам нужны нечеткие числа в дифференциальных уравнениях, которые обеспечивают оценки неизвестных параметров.

Что такое нечеткое множество?

В классическом наборе элемент либо входит в набор, либо нет. Нечеткие множества определяются в терминах классических множествX как -

A = {(x, μA (x)) | x ∈ X}

Case 1 - Функция μA(x) имеет следующие свойства -

∀x ∈ X μA (x) ≥ 0

sup x ∈ X {μA (x)} = 1

Case 2 - Пусть нечеткое множество B быть определенным как A = {(3, 0.3), (4, 0.7), (5, 1), (6, 0.4)}, то его стандартная нечеткая запись записывается как A = {0.3/3, 0.7/4, 1/5, 0.4/6}

Любое значение с нулевой степенью членства не появляется в выражении набора.

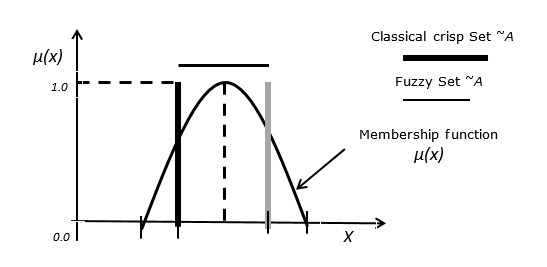
Case 3 - Связь между нечетким набором и классическим четким набором.

На следующем рисунке показана взаимосвязь между нечетким набором и классическим четким набором.