Графический алгоритм
Граф - это абстрактное обозначение, используемое для представления связи между парами объектов. График состоит из -
Vertices- Связанные объекты в графе называются вершинами. Вершины также известны какnodes.
Edges - Ребра - это звенья, соединяющие вершины.
Есть два типа графиков -
Directed graph - В ориентированном графе ребра имеют направление, т. Е. Ребра переходят из одной вершины в другую.
Undirected graph - В неориентированном графе ребра не имеют направления.
Раскраска графика
Раскраска графа - это метод присвоения цвета вершинам графа таким образом, чтобы никакие две соседние вершины не имели одинаковый цвет. Некоторые проблемы с раскраской графа -
Vertex coloring - Способ раскраски вершин графа так, чтобы никакие две соседние вершины не имели одинаковый цвет.
Edge Coloring - Это метод присвоения цвета каждому краю, чтобы никакие два смежных края не имели одинаковый цвет.
Face coloring - Он назначает цвет каждой грани или области плоского графа, чтобы никакие две грани, имеющие общую границу, не имели одинаковый цвет.
Хроматическое число
Хроматическое число - это минимальное количество цветов, необходимое для раскрашивания графика. Например, хроматическое число следующего графика - 3.

Концепция раскраски графиков применяется при составлении расписаний, присвоении частот мобильной радиосвязи, судуку, распределении регистров и раскраске карт.
Шаги по раскраске графа
Установите начальное значение каждого процессора в n-мерном массиве равным 1.
Теперь, чтобы назначить конкретный цвет вершине, определите, назначен ли этот цвет соседним вершинам или нет.
Если процессор обнаруживает одинаковый цвет в соседних вершинах, он устанавливает его значение в массиве равным 0.
После выполнения n 2 сравнений, если какой-либо элемент массива равен 1, это допустимая окраска.
Псевдокод для раскраски графов
begin
create the processors P(i0,i1,...in-1) where 0_iv < m, 0 _ v < n
status[i0,..in-1] = 1
for j varies from 0 to n-1 do
begin
for k varies from 0 to n-1 do
begin
if aj,k=1 and ij=ikthen
status[i0,..in-1] =0
end
end
ok = ΣStatus
if ok > 0, then display valid coloring exists
else
display invalid coloring
endМинимальное связующее дерево
Остовное дерево, сумма веса (или длины) всех его ребер меньше, чем все другие возможные остовные деревья графа G, называется остовным деревом. minimal spanning tree или же minimum cost spanningдерево. На следующем рисунке показан взвешенный связный граф.

Некоторые возможные остовные деревья приведенного выше графика показаны ниже -



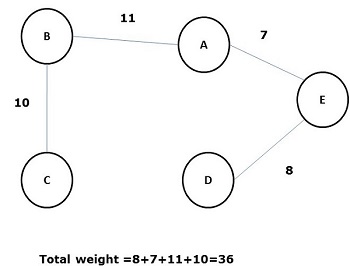



Среди всех вышеперечисленных остовных деревьев рисунок (d) является минимальным остовным деревом. Концепция остовного дерева минимальной стоимости применяется в задачах коммивояжера, проектировании электронных схем, проектировании эффективных сетей и разработке эффективных алгоритмов маршрутизации.
Для реализации минимального связующего дерева затрат используются следующие два метода:
- Алгоритм Прима
- Алгоритм Крускала
Алгоритм Прима
Алгоритм Прима - это жадный алгоритм, который помогает нам найти минимальное остовное дерево для взвешенного неориентированного графа. Сначала он выбирает вершину и находит ребро с наименьшим весом, приходящееся на эту вершину.
Этапы алгоритма Прима
Выберите любую вершину, скажем v 1 графа G.
Выберите ребро, скажем e 1 графа G, так чтобы e 1 = v 1 v 2 и v 1 ≠ v 2 и e 1 имело минимальный вес среди ребер, инцидентных v 1 в графе G.
Теперь, после шага 2, выберите минимально взвешенное ребро, приходящееся на v 2 .
Продолжайте это, пока не будет выбрано n – 1 ребро. Вотn количество вершин.

Минимальное остовное дерево -

Алгоритм Крускала
Алгоритм Краскала - это жадный алгоритм, который помогает нам найти минимальное остовное дерево для связного взвешенного графа, добавляя на каждом шаге дуги возрастающей стоимости. Это алгоритм минимального остовного дерева, который находит ребро с наименьшим возможным весом, которое соединяет любые два дерева в лесу.
Шаги алгоритма Крускала
Выберите кромку минимального веса; скажем, e 1 из Графика G и e 1 не является петлей.
Выберите следующее ребро с минимальным весом, подключенное к e 1 .
Продолжайте это, пока не будет выбрано n – 1 ребро. Вотn количество вершин.

Минимальное остовное дерево приведенного выше графа -
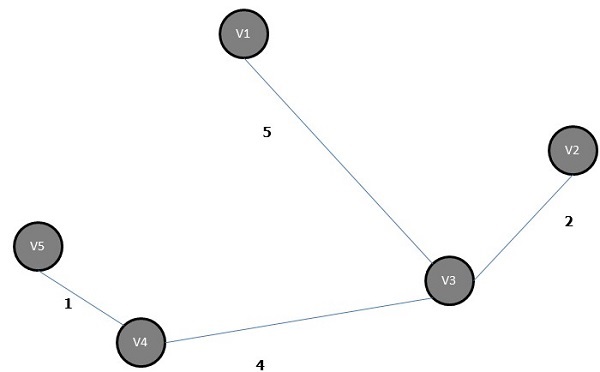
Алгоритм кратчайшего пути
Алгоритм кратчайшего пути - это метод поиска пути с наименьшей стоимостью от исходного узла (S) до конечного узла (D). Здесь мы обсудим алгоритм Мура, также известный как алгоритм поиска в ширину.
Алгоритм Мура
Обозначьте исходную вершину S и пометьте ее i и установить i=0.
Найдите все непомеченные вершины, смежные с вершиной, помеченной i. Если с вершиной S не соединены никакие вершины, то вершина D не соединена с S. Если есть вершины, соединенные с S, пометьте ихi+1.
Если помечено D, перейдите к шагу 4, иначе перейдите к шагу 2, чтобы увеличить i = i + 1.
Остановитесь после того, как будет найдена длина кратчайшего пути.