Физика - Сферические линзы
Введение
Прозрачный материал (обычно стекло), соединенный двумя поверхностями, одна или обе из которых имеют сферическую форму, известен как «сферическая линза».

Выпуклый объектив
Линза может иметь две сферические поверхности, выступающие наружу (как показано на изображении ниже), известная как выпуклая линза или двойная выпуклая линза.
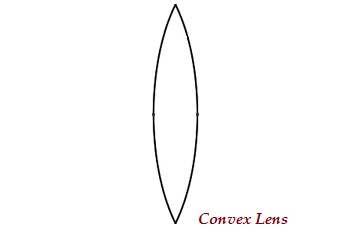
Средняя часть этой линзы выпуклая (толще) и с обоих концов узкая.
Выпуклая линза собирает световые лучи; поэтому он также известен какconverging lens.
Вогнутая линза
Линза может иметь две сферические поверхности, изогнутые внутрь (как показано на изображении ниже), известная как вогнутая линза или двойная вогнутая линза.
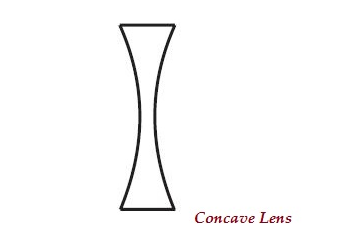
Средняя часть этой линзы узкая (загнута внутрь), а оба края толще.
Вогнутая линза рассеивает световые лучи; поэтому он также известен какdiverging lens.
Линза, вогнутая или выпуклая, имеет две сферические поверхности, и каждая из этих поверхностей образует часть сферы. Центры этих сфер известны какcenters of curvature, представленный английской буквой 'C. '
Поскольку есть два центра кривизны, поэтому они обозначены как «C 1 » и «C 2» .
Воображаемая прямая линия, проходящая через оба центра кривизны линзы, известна как principal axis.
Оптический центр - это центральная точка линзы. Он представлен 'O. '
Апертура - это фактический диаметр кругового контура сферической линзы.
Главный фокус объектива представлен 'F. '
У линзы обычно два фокуса, представленные как F 1 и F 2 .
Focal length- расстояние между главным фокусом и оптическим центром линзы. Он представлен 'f. '
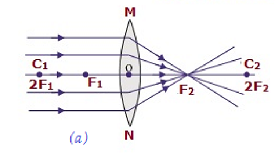
Следующая таблица иллюстрирует характер и положение изображений, формируемых выпуклой линзой.
| Положение объекта | Положение изображения | Размер изображения | Природа изображения | Образ |
|---|---|---|---|---|
| В бесконечности | В фокусе F 2 | Сильно уменьшенные, заостренные | Реальный и перевернутый |
|
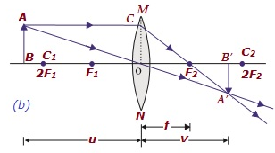
| За пределами 2F 1 | Ч / б F 2 и 2F 2 | Уменьшено | Реальный и перевернутый |
|
| На 2 этаже 1 | На 2 этаже 2 | Тот же размер | Реальный и перевернутый |
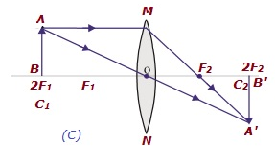
|
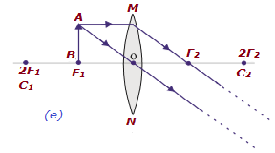
| Ч / б F 1 и 2F 1 | За пределами 2F 2 | Увеличенный | Реальный и перевернутый |

|
| В фокусе F 1 | В бесконечности | Бесконечно большой или сильно увеличенный | Реальный и инвертированный |
|
| Ч / б фокус F 1 и оптический центр O | На той же стороне линзы, что и объект | Увеличенный | Виртуальный и прямой |
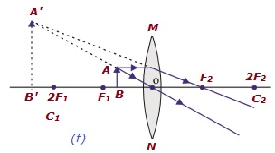
|
В следующей таблице показаны характер и положение изображений, сформированных вогнутой линзой.
| Положение объекта | Положение изображения | Относительный размер изображения | Природа изображения | Образ |
|---|---|---|---|---|
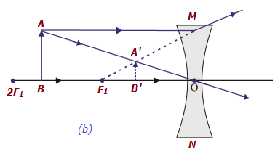
| В бесконечности | В фокусе F 1 | Сильно мелкий, заостренный | Виртуальный и прямой |
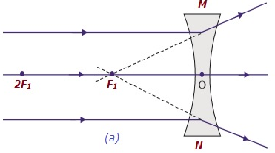
|
| Ч / б бесконечность и оптический центр O объектива | Ч / б F 1 и оптический центр O | Diminishe d | Виртуальный и прямой |
|
Формула линзы
Формула выражается как -
Формула линзы выражает отношения между объектом и расстоянием (т. Е. u), расстояние до изображения (т.е. v) и фокусное расстояние (т.е. f) объектива.
$$ \ frac {1} {v} - \ frac {1} {u} = \ frac {1} {f} $$